移动机器人路径规划算法综述

李晓旭，马兴录，王先鹏

(青岛科技大学 信息科学技术学院，山东 青岛 266061)

0 引言

随着科技的发展与产业变革，移动机器人被广泛应用于生产与生活的各个领域之中。由于机器人工作环境的不确定性与复杂性，如何快速准确地搜索出一条由初始状态至目标状态的无碰撞路径成为当前机器人避障的技术难点[1-2]。由于机器人任务的不同，评价路径的指标也存在一定的差异，一般通过最短路径、最短时间、最小能量消耗、安全性最高等指标评价选择最佳路径。性能优越的路径规划算法往往能够在不确定的复杂环境中规划出适合机器人运动的高效路径，这不仅能提高移动机器人的工作效率，还能降低移动机器人损耗。路径规划算法作为移动机器人的关键技术之一，已成为国内外研究热点[3]。

本文对主流的移动机器人路径规划算法进行总结综述，根据移动机器人路径规划算法的特性，将其划分为传统规划算法、智能规划算法以及基于采样的规划算法。随后对各类算法进一步划分，并介绍各种算法的原理以及其自身的局限性，同时总结分析各类算法的优缺点。最后，根据目前移动机器人路径规划算法的研究现状做出进一步展望，分析其发展趋势。移动机器人路径规划主流算法如图1所示。

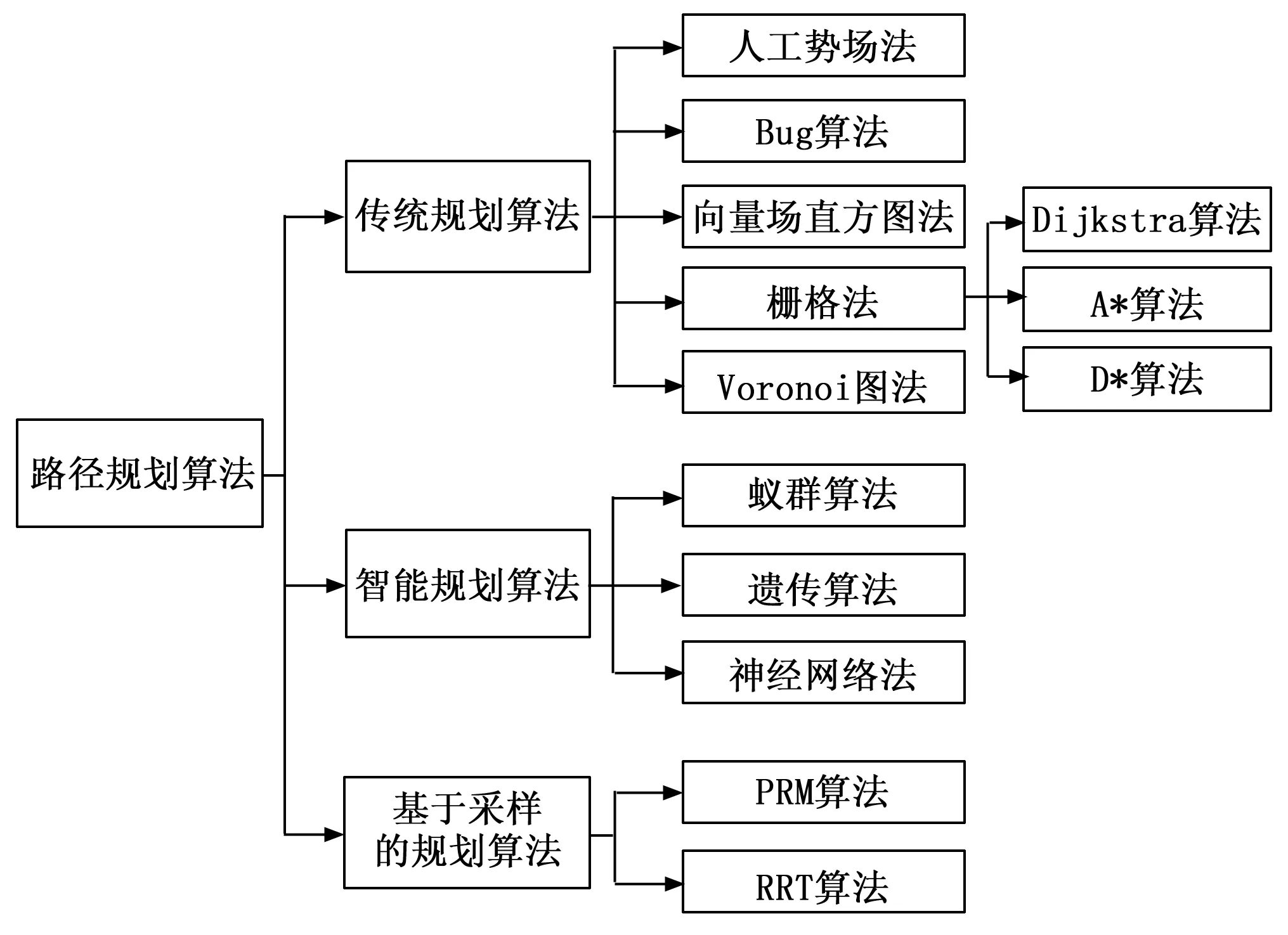
图1 移动机器人路径规划算法分类图

1 传统规划算法

传统规划算需要在结构化的环境内对障碍物进行准确地建模描述。该类算法依赖环境的显示表达。

1.1 人工势场法

Khatib在1985年提出了人工势场法(Artificial potential field，APF)[4]，用于移动机器人路径规划实现避障功能。该算法借助物理学中“势场”的概念，将障碍物等价位斥力源，对移动机器人产生“排斥力”；将目标点等价位引力源，对移动机器人产生“引力”。机器人在移动的过程中，“引力”与“斥力”不断发生变化，机器人通过本身所受的合力实时改变移动方向，实现移动过程中躲避障碍物。该方法实时性高，且实现结构较为简单，因此有一定的应用价值。人工势场法示意图如图2所示。

图2 人工势场法示意图

人工势场法自身具有局限性。当移动机器人处于障碍物附近时，规划的路径会产生“振荡”现象，这影响机器人在运行过程中的稳定性[5]。该方法容易出现局部极小值，例如当障碍物位于移动机器人与目标点的中心位置时，移动机器人所受“引力”与“斥力”相互抵消，此时机器人无法确定移动方向，进而导致路径规划失败。为此许多学者在不同方向上对此方法作出改进。Li G通过设置虚拟局部目标的方法克服人工势场法中的振荡效应[6]。丛玉华等[7]通过设置探测窗口、距离影响因子的方法解决了轨迹振荡以及轨迹不可达问题。邱博[8]等在斥力势能函数中引入变增益系数，解决了振荡问题。王兵根据环境信息动态设置虚拟目标点，快速逃离路径局部极小值点[9]。石为人[10]针对势力场局部极小值问题，提出一种拼接局部极小值区域分散障碍物的方法，实验证明，该方法较好地解决了局部极小值问题。Liu等[11]提出一种双势场融合自适应路径规划算法，提高了机器人对不同速度与不同障碍物场景的适应能力。

1.2 Bug算法

图3 Bug算法示意图

Bug算法结构较为简单，但使用该算法时，移动机器人在运动过程中仅依靠最新获得的数据，当传感器提供的信息不足时，容易导致规划失败。针对Bug算法的缺陷，学者们做出了很多研究。Bug2算法[13]对“边界跟踪”过程作出改进，一定程度上降低了移动机器人的路径代价。Kamon提出了Tangent Bug算法[14]，该算法引入路径代价函数，通过范围探测器辅助，动态选择机器人移动方向，进一步减少了移动机器人“边界追踪”过程中产生的代价。Dist-Bug[15]算法对遇到障碍物时，移动机器人绕行方向问题作出了改进。彭艳[16]提出了Multi-Bug算法，该算法加入爬虫分裂规则以及爬虫死亡条件判断规则，当移动机器人遇到障碍物时，通过爬虫分裂规则并行计算路径代价寻找最优路径，实验证明该算法较Dist-Bug算法在降低路径代价、实时性、通用性等方面皆有一定的提高。蔡存成[17]等在Bug算法中加入“避行”过程，通过避障转向角索引图与转向时机提前量控制移动平台躲避障碍物，并在“边界跟踪”过程中通过模糊控制器控制移动平台绕行的精确度。

1.3 向量场直方图法

Borenstein于1991年提出了向量场直方图法(Vector filed histogram，VFH)[18]。该方法将机器人周围的环境用直方图表示，因此该方法对处理传感器和建模误差要求非常高。该方法首先构建一个二维笛卡尔直方图栅格，并根据传感器数据实时更新栅格图。然后通过减少机器人当前位置周围的笛卡尔直方图，构建一维极坐标直方图。最后通过极坐标直方图上的候选波谷确定机器人移动方向。向量场直方图如图4所示，该极坐标系的两坐标轴分别表示以机器人为圆心感知到障碍物的角度、对应方向上障碍物可能存在的概率，一般情况下，极坐标直方图存在波峰与波谷，波峰表示障碍物密度较高，波谷表示障碍物密度较低，障碍物密度低于给定阈值的波谷成为候选波谷。

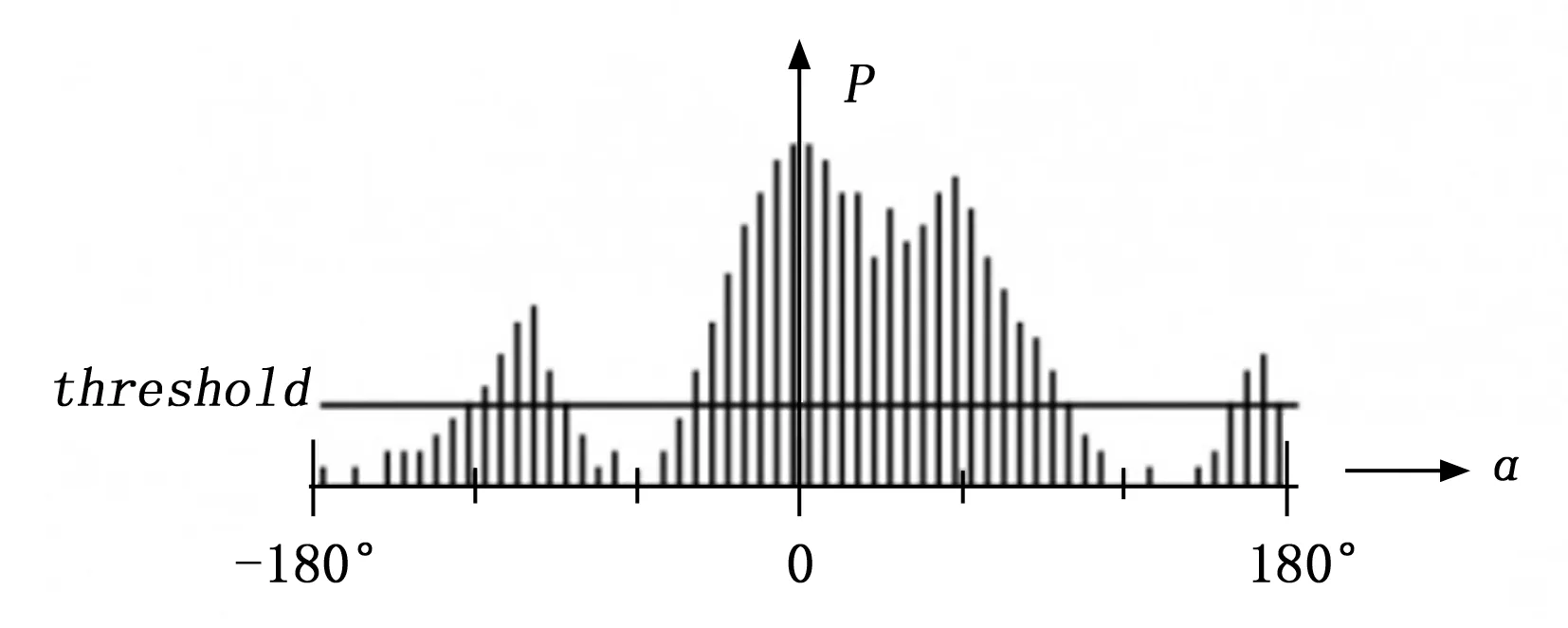
图4 向量场直方图

VFH算法具有可靠性高、计算效率高、鲁棒性强等优点，但是该算法不完备，在狭窄区域中，容易陷入局部极小值。Ulrich提出了VFH+算法[19]，该算法考虑了机器人的体型，提高了算法的通用性；通过阈值滞后增加了轨迹的平滑度；添加成本函数表征算法性能。Ulrich提出了VFH*算法[20]，该算法通过前瞻距离，探测并选择机器人的最佳移动方向。娄虎[21]等针对水面无人艇雷达避障问题，提出了一种自调节VFH+算法。改进后的算法能够根据无人船所处的位置对障碍物阈值进行实时更新，提高了无人船的灵活性。

1.4 栅格法

栅格(Grid map，GM)法将机器人所处的环境通过某种方法划分为具有局部环境信息的网格单元，即栅格[22]。如图5所示，栅格可分为自由栅格与占用栅格两种，其中占用栅格包含环境中的障碍物信息。将自由栅格按照一定的顺序构成连通图，并采用搜索算法在该连通图上构建一条由初始栅格至目标栅格的无碰撞路径，记为规划路径[23]。栅格法在规划速度方面性能优越，但其规划效率受栅格精度的制约。栅格法已被广泛应用于移动机器人，栅格法常用的搜索算法有Dijkstra最短路径算法、A*算法、D*算法等。

图5 栅格示意图

1.4.1 Dijkstra算法

1973年Johnson提出了Dijkstra算法[24]。Dijkstra算法多用于求解有权图中一个顶点到其他顶点的最短距离。该算法通过数组D保存起始点至各个顶点的最短距离，通过集合T保存已遍历的最短路径对应的顶点。执行算法时，通过迭代的方式，每次从集合T之外的顶点中求取距离起始点距离最小的顶点，将该点加入集合T中，并通过该点刷新数组D中的值，直至集合T中包含所有顶点。

Dijkstra算法具有很强的鲁棒性，且其能计算出两点之间的最优路径解，但是该算法是无向搜索算法，随着节点数量的增加，该算法的计算效率降低。基于Dijkstra算法的缺点，学者作出了许多改进。目前，有研究通过改变有权图中的权重标准改善Dijkstra算法的性能[25]，但是多数研究中通过限定搜索区域提高Dijkstra算法的搜索效率。例如，张超等[26]将搜索区域缩小为以起始点和目标点为对角线的矩形区域内，当该区域搜索不到路径时，逐渐扩大采样区域；宫金良等[27]按照路径权值、时间权值分别创建邻接矩阵，缩小了迭代过程中的最小路径搜索域和最优路径更新域；郭梦诗等[28]用连通域表示障碍物区域，并通过链表存储连通域中相邻节点的距离信息，使搜索范围保持在避障空间内；贾文友等[29]将起始点、目标点与障碍物通过数学方式构造凸包模型，将全地图路径求解问题转换为求解凸包内起止点至目标点最短路径问题。

1.4.2 A*算法

1972年Hart等人提出了A*算法[30]。A*算法本质上是一种启发式搜索算法，即通过一定的评价指标指引算法运行。A*算法引入了代价函数，并将其作为评价指标，代价函数如公式(1)所示。

f(n)=g(n)+h(n)

(1)

其中：g(n)代表节点n至起点的代价，是当前的实际代价；h(n)代表节点n至目标点的代价，是估计代价，一般通过节点n至目标点估计代价的额计算方法有两种：欧氏距离、曼哈顿距离；g(n)代表节点n的总代价。

A*算法的优点是计算方式简单、规划路径短等，但该方法计算量大，规划路径往往拐点较多。针对路径不平滑问题，Min Haitao[31]在启发式函数设计中加入了路径曲率的代价，提高了路径的平滑性。槐创锋等[32]将传统A*算法的搜索领域进行扩展，并通过优化搜索角度的方式提高了路径平滑度。也有一些研究通过对生成路径进行优化，增加路径平滑度。例如文献[33-36]结合Floyd算法思想优化路径；文献[37]通过B样条曲线平滑路径。针对传统A*算法计算效率问题，邹文等[38]在栅格地图上建立拓扑地图，通过A*算法在栅格地图上获取初始全局路径，然后结合Floyd算法思想在拓扑地图中对初始全局路径进行优化。通过该种方式，在优化过程中减少了大量计算，提高了其优化效率。其次，通过增加状态函数优化传统的动态窗口算法，并将其应用于局部路径规划的避障与移动，这也提高了获取路径的速度。还有一些研究通过优化评价函数提高算法计算效率[39-40]，也有很多研究通过融合A*算法与动态窗口提高算法速度，例如文献[32]、文献[33]、文献[36]、文献[40]。

1.4.3 D*算法

1994年Stentz提出了D*算法[41]，该算法由A*算法发展而来，适用于环境未知的或者环境存在动态变化的场景。D*算法对A*算法做了两个重要改进。

1)出现动态障碍物时，D*算法可以更新动态障碍物附近的栅格信息。

2)D*算法的启发函数可传递。当中心栅格向周围栅格扩展时，可将其启发值传递给周围邻点。

D*算法的代价公式由A*函数发展而来，如公式(2)所示。

F(s)=G(s)+H(s)

(2)

其中:G(s)为起始点至s的代价值，H(s)为启发值，其计算方式如公式(3)所示。

(3)

式中，s′为s的拓展节点，H(s′)为s′的启发值，C(s,s′)为相邻节点的代价值，sgoal为目标点。进行栅格扩展的过程中，被扩展节点s的启发值由其拓展点s′的代价值以及拓展点s′的启发值计算得来。D*算法启发函数示意图如图6所示。

图6 启发函数示意图

D*算法对A*算法有一定的提升，其搜索路径的速度更快、路径更为优异，但是D*算法并没有改善路径曲折的缺点，而且D*算法规划的路径贴近障碍物边缘。与A*算法类似，对于D*算法的改进主要集中于两个方面：提高路径平滑度、提高搜索效率。一些研究通过缩小搜索区域提高算法的搜索效率，例如文献[42]、文献[43]引入Voronoi图法在一定程度上缩小搜索路径；有一些研究通过优化节点选择方式等方法，对D*算法进行单次优化，提高算法搜索效率，例如文献[42]引入二级子节点概念放弃扩展无用节点、文献[44]引入跳点搜索与元胞邻居结构跳过对无用节点的扩展、文献[45]通过导向函数限制单次搜索节点范围；还有一些研究通过更改代价函数缩小搜索空间，例如文献[48]在代价函数中增加碰撞因子，放弃在可能存在碰撞的区域内搜索路径，一定程度上提高了路径搜索效率。对于路径平滑的改进思想主要有两种：路径生成中考虑平滑处理、路径生成后进行平滑处理。在路径生成过程种对路径进行平滑处理主要通过更改代价函数实现，例如，文献[43]增加产生尖角的节点的启发值，减少拐点；文献[45]在原有代价函数基础上增加平滑度函数，增加路径平滑度。对生成路径的平滑工作一般通过借助数学理论实现，例如文献[46]、文献[47]引入三次B样条对生成的路径进行平滑处理。

1.5 Voronoi图法

Voronoi图法采用路径距离尽可能远的方式划分自由空间[48-49]。Voronoi图法的核心思想是通过一系列种子点将空间划分为若干个子区域，每个子区域中点到该区域对应的种子节点的距离小于它们到其他种子节点的距离。通过该特性，将空间中障碍物边界取做种子节点，则每个子区域的边界都可以作为移动机器人无碰撞路径的一部分。将机器人的初始点和目标点分别连接到Voronoi图上，采用搜索算法可获得由初始点至目标点的无碰撞路径。

Voronoi图能够使机器人与障碍物保持一定的距离，这提高了机器人运行的安全性，但是该方法获取的路径代价较大，且在高维空间的规划能力较差。针对移动机器人在动态环境中的路径规划问题，Ayawli等[50]提出一种基于Voronoi图和计算几何技术的动态路径规划算法。该算法使用Voronoi图以几何形状计算路线图，并将节点添加到初始路线图节点以计算用于重新规划的新路径，在后续重新规划路径值前，失效节点被丢弃，从而节省时间与空间资源。实验结果表明，该算法可以在复杂和动态的环境中实现安全、更少的路径成本和时间的路径规划计算。Hu等[51]提出一种深度学习强化的基于Voronoi的多机器人协同探索算法。该算法通过Voronoi图法动态划分环境区域，然后通过将分区中不同的目标位置分配给各个机器人来最小化重复的探索区域。实验结果表明，该算法可以确保每个机器人探索区域时而不会与其他机器人发生冲突，从而最大限度地减少任务完成时间并节省更多资源和能源。

由上述可知，传统的移动机器人路径规划算法需要对环境进行建模与描述。因此，随着环境复杂度的增加传统路径规划算法的搜索效率将大大降低。

2 智能规划算法

智能算法具备一定的学习能力，对环境的适应能力强，能够在规划中不断获取新的信息用于优化路径。

2.1 蚁群算法

1991年Colorni与Dorigo提出了蚁群算法(ACO，ant colony optimization)[52]，该算法是一种仿生学算法，受蚂蚁觅食行为启发而来。蚂蚁觅食偏向于走信息素高的路径，蚂蚁觅食示意图如图7所示。蚁群算法被广泛应用于移动机器人动态路径规划中。

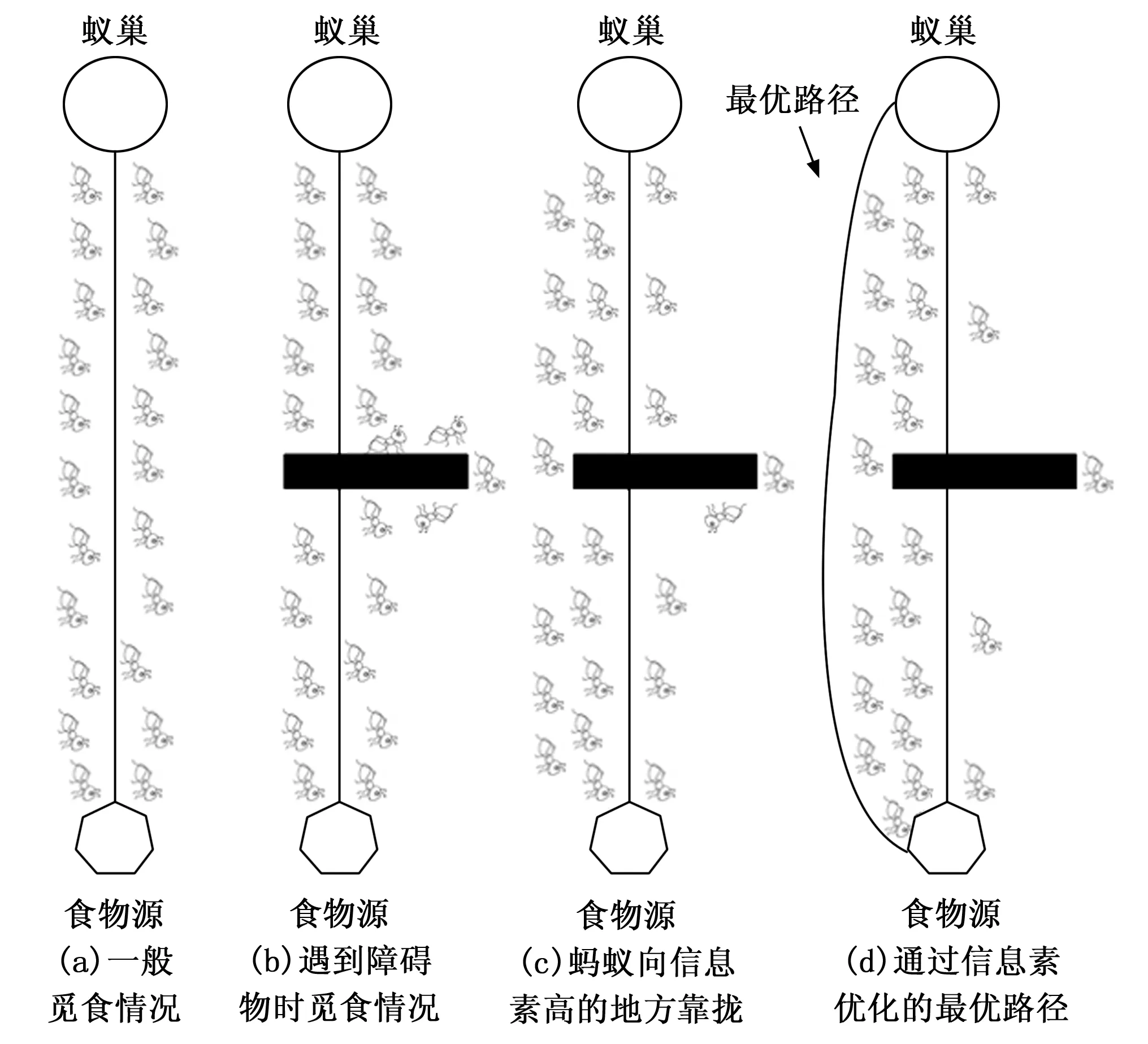
图7 蚂蚁觅食示意图

蚁群算法虽然具有较高的鲁棒性，但是该算法容易出现局部最优问题。针对该缺点，许多学者对蚁群算法作出改进。Sangeetha等[53]提出一种基于智能增益的蚁群路径规划算法并将其应用于无人地面车辆(UGV,unmanned ground vehicles)。当UGV遇到障碍物时，会在障碍物周围构建许多路径，因此需要耗费大量时间选择最优路径。该算法通过消除需要穿越障碍物周围所有的路径减少能量。实验结果证明，该算法相对于传统ACO算法在获取路径速度上有一定的提升，但是该方法对路径代价的优化效果不明显。基于此点，陈礼琪[54]在文献[53]的基础上对ACO算法作出了改进。该算法通过更改转移概率公式，减少蚂蚁陷入死区间，即解决了局部极小值问题；通过增益函数更改信息素函数，提高算法搜索效率。实验结果证明，与传统ACO算法相比，该算法不仅提高了算法的搜索效率，还降低了路径代价。对于蚁群算法优化问题，一些研究通过优化信息素更新方式提高算法效率[54-57]；一些研究通过算法融合弥补ACO算法缺陷[58-61]。

蚁群算法采用分布式计算方式，对多个个体同时计算，每个个体在实时感受环境变化的同时，通过释放信息素改变周围环境。蚁群算法的正反馈机制使得个体逐渐向信息素高的地方靠拢，这使该算法在搜索路径的过程中不断收敛。但是该算法中，初始信息素值相同，因此在选择下一节点是倾向于随机选择，这导致该算法需要较长时间才能发挥正反馈作用，从而降低了算法收敛速度。当蚁群算法获得的初始解为次优解时，正反馈机制很容易使得次优解占据优势，即使得算法陷入局部最优，而且难以逃出局部最优。另外，蚁群算法参数众多且具有一定的关联性，通过调整参数可以提高蚁群算法的性能，但是参数的调整依赖于经验和试错。因此，对于蚁群算法的优化除了上述研究的改进外，还可以对信息素的初始化方式进行改进，为算法提供较好的探索方向，不仅可以解决局部最优问题，还可以提高算法收敛速度。另外，对蚁群算法的结构进行优化也具有重要意义，通过改进参数的关联方式、对参数进行优化，可以增加算法的可调性，提高算法优化能力。

2.2 遗传算法

1958年，Bremermann首次提出遗传算法(GA，genetic algorithm)概念[62]。遗传算法是一种模仿生物体在繁衍后代过程中自然遗传、进化的全局优化算法，主要包括路径编码、构建适应度函数等过程。该算法可以并行地对解空间的不同区域进行搜索，使得搜索趋于最优解，从而克服传统优化算法容易陷入局部极小值的缺点。该算法被广泛应用于移动机器人路径规划场景中。

遗传算法运算速率较低，且在运算过程中占用大量计算机资源，这也是制约其发展的主要因素。针对遗传算法的改进问题，学者们做了大量研究。针对传统遗传算法收敛速率慢、局部搜索能力差问题，王豪等[63]提出一种改进的自适应遗传算法。该算法通过改进适应度评估指标与轮盘赌选择方法提高了算法的搜索效率。实验表明，该算法获得的平均路径比传统遗传算法缩短了9.9%，且算法迭代次数也相应地减少。针对遗传算法局部局部极小值问题，王吉岱等[64]提出了一种模糊自适应遗传算法，该算法结合模糊逻辑算法动态自适应调整交叉和变异算子。另外，在适应度函数中引入余弦函数平滑度评价因子，减少了路径的拐点，提高了路径的平滑度。实验表明，该算法与自适应遗传算法相比，收敛速度更快，且锐角拐弯次数减少了45.16%。针对传统遗传算法局部最优问题，Qu等[65]通过协同进化机制改进遗传算法。该算法通过改进遗传算子与适应度函数，解决了遗传算法局部最优解问题并提高了收敛速度；另外，通过协同机制避免了机器人之间的碰撞，使得该算法可以应用于多机器人路径规划。Nazarahari等[66]提出一种增强遗传算法结合，该算法通过5个定制的交叉和变异算子，解决了传统遗传算法初始解迭代多次无法获取最优解问题，另外该算法增加了碰撞消除算子，使其可以应用于多移动机器人路径规划中。

遗传算法与蚁群算法类似，都是从群体的角度出发，对多个个体并行计算，在一定程度上提高了一定效率。该算法使用概率方式进行迭代，具有一定的随机性，而且在搜索过程中使用评价函数启发，实现过程相对简单。与蚁群算法类似，该算法参数较多、参数关联性强，而且参数取值对算法的性能影响较大，但是，对参数的调整往往依赖于经验。因此诸多学者通过优化参数实现对算法的优化，例如文献[66]。与蚁群算法相比，遗传算法对网络反馈信息的利用率较低，因此收敛速度较慢，所以更改遗传算法结构，提高算法对反馈信息的利用率，可以加快算法收敛速率。遗传算法对初始种群的选择具有一定的依赖性，因此，通过启发式方法选择更为优异的初始种群，可以提高算法的效率。

2.3 神经网络法

神经网络(NN，neural network)算法是在研究人脑工作机理的基础上提出来的，具有较好的学习、容错能力[67]。该算法的基本思想是构建一个针对移动机器人路径规划的神经网络模型。该模型的输入为传感器信息以及机器人上一次的运动状态[68]。

神经网络方法可使机器人具备适应新环境的能力，但需要事先构建数据集训练模型，而且训练时间较长。因此，往往将神经网络算法与其他智能算法相结合，以改善神经网络的规划性能。文献[69]与文献[70]将神经网络与遗传算法相结合应用于移动机器人路径规划，实验结果证明了该方法的可行性；文献[71]融合神经网络与混合粒子群算法实现了移动机器人路径规划；文献[72]与文献[73]将模糊神经网络应用于路径规划，并证明了该算法的高效性。文献[74]将使用自适应蚁群优化算法和人工神经网络迭代方式解决路径规划问题，试验证明该方法获取路径的速度更快。文献[75]提出一种概率路线图与神经网络结合的路径规划算法实现了移动机器人动态路径规划。

神经网络结构中包含大量的参数，参数的数量往往比蚁群算法、遗传算法等其他智能算法更多，且参数关联性更强，对算法效率影响更明显。因此，在构建神经网络时，调参过程较为复杂，且通常会占用大量时间，这大大限制了神经网络的应用。另外，神经网络需要大量的数据对模型进行训练，数据量的大小间接影响算法的性能。目前，神经网络在路径规划领域的应用相对较少，因此，可用的公开数据集较为匮乏。学者往往需要通过大量数据事先构建数据集，这增加了神经网络的实现难度。即便目前已有大量研究融合神经网络与各种智能算法，例如蚁群算法、粒子群算法、遗传算法等，但将融合算法应用于移动机器人路径规划的研究不是很多。神经网络缺陷较为明显，但是优异的网络架构往往能使算法具有强大的环境适应能力。随着移动机器人应用场景的增加，其面对的工作环境复杂度进一步增加，神经网络的优势将进一步展现。因此，将神经网络应用于移动机器人具有重要意义，未来工作中需要对该应用场景做大量研究。

3 基于采样的规划算法

基于采样的方法通过碰撞检测判断候选路径采样点的可行性，从而避免了对环境约束的显示表达(不需要对环境建模)。该种方法通过连接所有可行采样点，进而形成可行路径图，最后在该路径图中求解一条由初始状态至目标状态的可行路径。基于采样的规划算法基本框图如图8所示。目前常用的基于采样的规划算法是概率路线图(PRM，probabilistic roadmaps)法和快速扩展随机树(RRT，rapidly-exploring random tree)法。

图8 基于采样的规划算法框图

3.1 PRM算法

1996年Kavraki 和 Svestka[76]提出了PRM算法，该算法是一种基于多次查询的规划算法，包括学习和查询两个阶段。在学习阶段，通过自由配置空间随机生成可行采样点，并使用快速的路径规划器连接这些可行采样点，从而构成概率路线图；在查询阶段，可以在概率路线图中寻找一条由初始状态至目标状态的最佳路径。如图9所示。

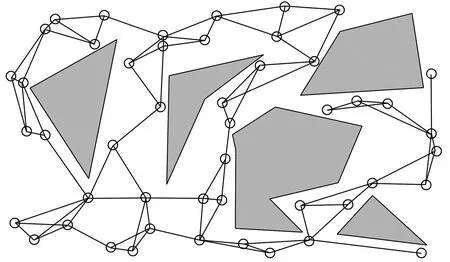
图9 PRM算法路径规划示意图

PRM算法在高维空间中表现优异，因此该算法得到了广泛关注与研究。但在一些应用场合中，获得先验路标的计算量可能太大甚至导致规划失败，这限制了该算法的在线规划能力。当采样点较少时，PRM算法规划的路径难以通过狭窄通道；增加采样点数量，可以解决该问题，但是计算代价增大。针对该问题，Ravankar等[77]提出一种基于混合潜力的概率路线图算法，该算法利用地图分割来产生高潜力和低潜力的区域，并在路线图构建过程中减少样本集分散。实验结果表明，该方法的局部和全局规划成功率中均高于95%；Zhong等[78]通过识别狭窄通道并增加狭窄通道中路标密度的方式，提高了路径规划的效率以及成功率。程谦等[79]通过改变连接点距离的方式，一定程度上提高了搜索路径的效率。针对PRM在采样点较少时难以规划出路径的问题，邹善席[80]等通过随机采样点生成函数将落在障碍物内的采样点变换到自由空间内，提高采样点的利用率；另外通过节点增强法实现了对路径的优化。实验结果表明，相对于传统的PRM算法，该算法的路径规划时间更短，且路径代价也相应的降低。

3.2 RRT算法

1998年Lavalle提出了RRT算法[81]，该算法通过构建随机树的方式获取由起始点至目标点的无碰撞路径。RRT算法将起始点作为随机树的根节点，通过随机采样的方式获取随机点，并将符合条件的点(与随机树中叶子结点相连时不与障碍物发生碰撞)加入随机树中作为叶子结点，直至目标点被加入到随机树中，算法迭代结束。RRT算法扩展过程示意图如图10所示。

图10 RRT算法扩展过程

RRT算法简单，对环境适应性强，而且可用于实时在线规划[82]。但是RRT算法对空间的探索完全随机，因此搜索效率较低；另外，RRT算法对路径缺乏优化能力。针对RRT算法的局限性，学者们做了大量研究。Kuffner等[83]提出了Bi-RRT算法，通过以起始点与目标点分别为根节点同时扩展随机树的方式，提高路径搜索效率。Karaman和Frazzoli[84]提出了RRT*算法，该算法通过重选父节点、重布线两种方式优化RRT算法，一定程度上降低了RRT算法的随机性。虽然随着空间维度的增加，RRT*算法收敛速度有所下降，但是RRT*算法具备渐进优化能力，因此学者们基于此算法作出了大量改进性研究。结合文献[83]的思想，Jordan和Perez[85]提出了Bi-RRT*算法。Nasir等[86]提出一种在规划过程中可根据在线信息调整参数的RRT*-Smart算法，以便适应诸如迷宫、狭窄通道等多类型环境。

虽然以上改进算法的速率有一定提升，但仍难满足高维空间的规划需求。由此诞生了启发式RRT算法，该种算法通过直接改变采样点的生成方式，降低路径的随机性和代价。Urmson等提出了基于启发式引导hRRT算法[87]，该算法结合启发式函数生成有效节点，引导随机树生长方向。Gammell等[88]提出了Informed RRT*算法，该算法在RRT*算法的基础上利用启发式方法对路径进行了优化。当获取初始路径后，该算法将采样空间限制在特定的超椭球区域内，进而提高路径优化的收敛速率。基于该思想学者们做出了许多研究与改进[89-91]。Gammell等[92]提出了BIT*算法，该算法采用批采样方式与超椭球优化机制相结合的方式，提高了获取路径速率的同时，降低了路径代价。Strub等[93]提出了一种自适应启发树算法(Adaptively Informed Trees，AIT*)，该算法通过使用非对称双向搜索来适应每个问题实例，以同时估计和利用特定问题的启发式，这使得其能迅速找到初始解并收敛到最优。另一种启发方式是基于目标偏向的，即goal-biasing RRT算法。该算法包括随机扩展和目标扩展两种方式，并在扩展过程中以一定概率选择扩展方式。许多研究基于此思想对RRT算法作出改进[94-96]。Noreen等[97]将路径搜索区间限定在包含起始点与目标点的可调边界区间内，增加了随机树生长的方向性。

4 路径规划算法分析

本文对目前主流的路径规划算法进行简单的归纳综述，列举相关算法的实现机制与原理、优点以及局限性，结果如表1所示。

表1 主流路径规划算法汇总表

现有的规划算法及其改良算法都已经应用于移动机器人路径规划之中，但是大多数研究都是将规划算法用于单个移动机器人，对于多机器人协同规划的算法相对较少。

传统的路径规划算法依赖于环境中障碍物的显示表达，即需要描述环境中的障碍物。例如，Bug算法在运行过程中需要对遇到的障碍物执行“边界跟踪”操作；基于栅格的算法需要构建环境栅格地图；向量场直方图算法需要根据障碍物密度构建极坐标系等。虽然各种算法对环境的表达方式略有不同，但都依赖于环境，这使得传统算法受环境约束较大。例如，Bug算法只适用于二维环境，当环境维数增加时，Bug算法将无法执行“边界跟踪操作”。传统算法的结构简单，这使得大多数算法的计算速度更快。一般而言，计算方式越简单，其收敛速度越快。栅格法与Voronoi法都是基于图形的算法，这些算法往往需要构建路径图形，该操作占用了一定的计算资源，因此相对于人工势场法、Bug算法、向量场直方图法，基于图形的算法收敛较慢。虽然栅格法、Voronoi法的收敛速度较慢，但是其路径优化能力更优越，获得的路径往往代价更低，而且对于环境的适应能力有一定提高，具有更强的鲁棒性。环境维度越高，该特性越明显。结构简单的算法对环境的适应力较差，人工势场法在特殊环境下(例如，引力与斥力相抵消)、Bug算法与向量场直方图算法在复杂环境下(例如迷宫)，容易陷入局部极小值，进而导致规划失败。基于图形的算法虽然牺牲了规划效率，但其较为复杂的结构使其性能得到提升，一定程度上解决了局部极小值问题，且对环境的适应能力有一定的提高。

相对于传统算法，智能算法结构更为复杂，而且智能算法自身具有强大的学习能力，这使得其对环境的适应能力非常强，减少了环境对算法的约束，极大程度上避免出现局部极小值问题。蚁群算法、遗传算法、神经网络算法都具有较多的参数，往往需要调参提高算法性能。蚁群依靠信息素的浓度变化实现对路径的渐进优化，当初始解为次优解时，蚁群算法容易出现局部最优问题。遗传算法克服了此缺点，遗传算法通过交叉和变异操作使算法的渐进优化能力更强。但遗传算法的交叉和变异等过程需要大量计算，因此在获得优化性能的同时，降低了算法的收敛速度。神经网络算法的结构更为复杂，该算法通过模拟人脑机理，对模型参数渐进优化。该算法的显著特点是需要大量数据训练模型，数据量越大，模型越精确，这也体现了该算法强大的学习能力。神经网络算法往往需要结合其他智能算法实现性能的提升，例如通过神经网络模型为遗传算法适应度函数提供更为合理的输入。

基于采样的算法不需要对障碍物进行显示描述，因此进一步降低了环境约束，这使得该种算法适用于高维空间的路径规划。但该算法的显著特点是随机性较大，生成路径的代价较高。PRM算法在学习阶段通过采样点构建网络图，在查询阶段通过搜索图获取路径。对图的操作，使得PRM算法浪费大量的计算资源，因此规划速率较慢。随着环境维度的增加，构建与查询图所消耗的时间随之增加，因此该算法不适用于复杂环境下移动机器人动态路径规划。RRT算法通过随机树的方式扩展路径，虽然该方式随机性较大，但其扩展速度极快，因此算法收敛更快，更能满足规划的实时性需求。随着环境维度的增加，其速度优势更为显著。RRT算法的随机性使获取路径的代价有所提升，且算法性能不稳定。

以上所有算法都具有其本身的优势与适用场景，但是往往其局限性限制了自身的发展，因此大量的工作用来优化划算法。

5 路径规划算法发展趋势

本文总结综述了移动机器人路径规划主流算法的原理、优缺点、研究现状及其改进方法，并将其分为三类：传统规划算法、智能规划算法、基于采样的规划算法。接下来对路径规划技术做出以下展望。

1)更为高效的算法融合：

目前，对于算法的大部分研究工作都是基于算法本身特性进行改进，对算法进行融合的研究相对较少，但是这些工作都取得了不错的效果，例如文献[35]、文献[38]、文献[50]、文献[60]等。单一的算法都具有各自的局限性，例如局部极小值、路径拐点多、规划效率低等问题，而并不是所有算法都具有相同的局限性，因此可以通过将互补的算法进行融合，实现更为高效的规划方式。例如将A*算法与蚁群算法进行融合，引入A*算法的评价函数优化蚁群算法的信息素更新方式，既加快了算法的收敛速率又克服了局部极小值问题。因此多算法融合是未来实现高效路径规划的重要方式。

2)多传感器融合的动态路径规划：

现有的路径规划算法多用于离线规划，即假定环境不变的情况下进行路径规划。然而实际应用场景往往是动态的，移动机器人需要及时躲避动态的障碍物。因此，动态路径规划算法在未来发展中需要投入大量研究。在动态路径规划中，往往需要实时更新环境信息，各种传感器可以用来实现对动态场景的更新。例如，深度相机、雷达等都可以实时传递环境中的障碍物距离以及形状信息，可以用于实时判定机器人与障碍物之间的距离。将多传感器应用于移动机器人并融合传感器信息可以实现更为精确的路径规划，甚至实现更为复杂的功能。

3)复杂环境中的路径规划：

现阶段，路径规划算法在规划过程中往往将初始位置与目标位置用点代替，该种方式较为简单；而且一些传统的路径规划算法仅适用于二维环境，大多数算法在环境维度提高、障碍物增多时，规划效率降低。现有的应用实例中，大多将移动机器人应用于简单的生活场景中，例如扫地机器人。现实的工作场景往往是复杂的，因此，提高路径规划算法在复杂场景下的规划效率具有重要意义。

4)物联网技术协同规划：

目前的应用场景中，大多是移动机器人自身通过计算单元实现路径规划功能。随着市场需求的增加，移动机器人被应用于各种复杂场景是必然趋势，而面对复杂场景时，移动机器人所处理的数据将大大增加，这使得对移动机器人的核心处理单元要求非常高。随着物联网技术的发展，数据可以通过互联网快速传输。因此将移动机器人需要处理的大量数据通过网络传输给高性能远程服务器处理，不仅能提高移动机器人的规划效率，还能在一定程度上简化移动机器人自身结构。

5)优化已有算法的规划性能：

已有的算法虽然具有一定的局限性，且大多应用于简单规划场景，但是基础算法仍有其适用场景，并且这些算法是实际应用的重要基础。因此，针对不同的路径规划算法对其自身局限性进行优化仍有重要意义，未来的工作中可以探索将更多的数学理论应用于优化路径规划算法，例如改进蚁群信息素更新方式、改进A*与D*算法的代价函数、优化遗传算法的适应度函数等。对基础算法的改进对未来的实际应用仍具有重要研究价值。

6 结束语

路径规划算法是移动机器人的关键技术，目前的路径规划算法具有一定的局限性，仍需要大量工作进行改进，提高算法的性能与适用性。随着人工智能技术的发展，多技术融合为路径规划算法的发展提供了发展契机。通过提升路径规划算法的性能与适用性，可以使移动机器人的应用场景更稳广阔