一种基于深度强化学习的机动博弈制导律设计方法
朱雅萌 张海瑞 周国峰 梁 卓 吕 瑞
中国运载火箭技术研究院,北京 100076
0 引 言
突防策略是决定高速机动飞行器突防能力的关键因素[1]。目前常用的突防策略是大范围机动,即在原有的飞行轨迹上叠加一个规律的周期性机动,包括螺旋机动[2-3]、蛇形机动[4-8]等。然而,现有的这些机动方法是射前装订的,不能根据拦截方的情况调整自己机动的时间和方向,导致适应性不强。特别是,如果遭遇拦截方的时间早于机动开始时间或处于机动指令的波节处,就会极大地影响突防效果[6-8]。此外,高速机动飞行器飞行过程中自身运动状态也存在一定不确定性[9]。与此同时,针对拦截方的探测手段是当前热门的研究方向,实时获知拦截方的信息在将来会成为可能,为基于双方信息的针对性突防策略提供了硬件基础。
在针对性突防策略中,目前研究较多的是以微分对策为代表的理论方法。微分对策理论是将突防拦截问题看作两点边值的双向极值问题,通过求解系统的黎卡提微分方程得到最优策略。Singh等[10]、Garcia等[11-12]与Liang等[13]采用微分对策理论解决目标-攻击者-防御者的三方博弈问题。毛柏源等[14]将突防拦截问题转换为两方零和博弈问题,并推导了解析形式的捕获区。魏鹏鑫等[15]基于线性二次型微分对策理论,解析推导了攻防双方过载能力的关系。然而,微分对策理论目前多适用于线性系统,否则黎卡提方程难以求得解析解。在实际的突防拦截问题中,动力学过程使得系统十分复杂,全部进行线性化处理会损失较大的拟真度。
人工智能技术的发展,使得借助智能算法解决突防拦截问题成为可能。智能算法主要分为深度神经网络(Deep Neural Network, DNN)和强化学习(Reinforcement Learning, RL)2种算法。DNN是由大量处理单元互联组成的非线性、自适应信息处理系统,适用于拟合非线性系统。而RL算法是一种无模型的机器学习方法,通过与环境交互自主寻找最优策略,适用于离散空间的决策问题。吴其昌等[16-17]采用数值算法求解微分对策问题,并尝试了利用DNN拟合同一问题并求解的可能。Rizvi等[18]采用输出反馈的RL算法解决离散时间线性二次调节器问题。Odekunle等[19]将RL算法、微分博弈论和输出反馈结合用于基于数据的控制器。
新兴的深度强化学习(Deep Reinforcement Learning, DRL)算法将RL算法和DNN相结合,融合了二者的优势[20],使得智能体能够在连续空间内自主寻找最优决策。突防拦截问题处于连续的状态空间和动作空间中,将DNN与RL算法结合能更切合地处理这类问题。谭浪等[21]基于深度确定性策略梯度算法DDPG设计了一种追逃博弈算法,但仅在小车上进行了验证。
本文基于DRL算法提出了一种机动博弈制导律,并以增大交会摆脱量为导向设计了回报函数。经仿真分析得到,在遭遇高速机动拦截方时,该制导律使飞行器能够根据信息实时自主决策,完成突防。与传统的蛇形机动相比,应用该制导律的交会摆脱量显著提升,且突防效果较稳定。
1 突防制导问题描述
本文研究一对一的突防拦截问题,假设进攻方在下压点之前完成突防,双方都为轴对称无动力飞行器,拦截方机动能力强于进攻方。将双方视为质点,考虑地球自转等因素,在三维空间中对仿真场景建立数学模型。
1.1 运动学模型
在三维笛卡尔坐标系下建立模型,以A,D分别代表进攻方和拦截方,突防拦截场景如图1所示,相应的运动学方程为:
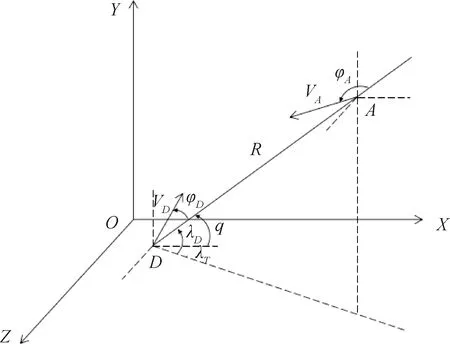
图1 突防拦截场景示意图
(1)
式中,进攻方和拦截方的运动速度分别为VA和VD,R表示双方斜距,q表示视线角,φA和φD分别表示进攻方和拦截方的前置角,λT表示双方视线所在的纵平面与基准坐标系X轴的夹角,λD表示双方视线与水平面的夹角。
1.2 动力学模型
进攻方和拦截方采用相同的动力学模型。在发射惯性系下建立飞行器的三自由度动力学模型如式(2)~(8)所示。
质心运动动力学方程:
(2)
附加方程:
(3)
(4)
(5)
(6)
(7)
h=r-R
(8)
式中:m表示飞行器质量;t表示时间;x,y,z表示飞行器在发射惯性系下的位置;v表示飞行器的速度;AB表示飞行器箭体系到发射惯性系的坐标转换矩阵,CA,CN和CZ表示轴向、法向和侧向的气动力系数,q表示动压,Sm表示飞行器参考面积;r表示飞行器质心的地心矢径,ωe表示地球自转角速度,gr,gωe分别表示重力加速度g在r,ωe方向上的分量;R0表示发射点的地心矢径;φ表示飞行器的地心纬度,ae和be分别表示地球椭圆模型的长半轴和短半轴;R表示飞行器下方地面到地心的距离,h表示飞行器的飞行高度。
1.3 双方制导律
1.3.1 拦截方制导律
拦截方采用针对进攻方的比例导引律,在视线系中可以表示为:
(9)
式中,NcS表示拦截方在视线系的需用过载;vc表示相对速度大小;λD和λT分别为高低角和方位角;GSL表示地球表面重力加速度,取值为 9.80665m/s2。
将需用过载和重力加速度转换到箭体系后相减以获得角度指令。由于拦截方做无动力飞行,可使用的过载垂直于箭身,因而X轴方向的过载不用于生成箭身姿态角度指令。过载转换及角度指令计算公式可以表示为
(10)
αCX=f(NcBy)
(11)
βCX=f(NcBz)
(12)
式中,NcB表示拦截方在箭体系的需用过载,g表示惯性系下质心处重力加速度,SB和AB分别为视线系和惯性系到箭体系的坐标转换矩阵,αCX和βCX分别表示指令攻角和指令侧滑角,f表示将过载转换为指令角的公式。
1.3.2 进攻方制导律
在不机动的情况下,进攻方处于平飞状态,其制导律在本文称为平飞基础制导律。此时,进攻方在视线系下的需用过载指令近似为常值,可以表示为:
(13)
式中,KM1和KM2为常数。
基于DRL算法的机动博弈制导律则是采用DRL方法来拟合进攻方的制导指令,根据进攻方和拦截方的位置和速度实时算得基准坐标系内的需用过载,可以表示为:
NcT=h(x,y,z,vx,vy,vz)
(14)
式中,NcT表示基准坐标系的需用过载,x,y,z,vx,vy,vz为双方的位置和速度,h表示DRL方法所拟合的制导规律。
进攻方角度指令的生成方式与拦截方相同,也是将需用过载转换到箭体系后舍弃X轴分量,分别用Y轴和Z轴分量生成攻角指令和侧滑角指令。
2 基于深度强化学习的机动博弈制导律设计
2.1 深度强化学习
DRL算法是一类通过与环境交互自主寻找最优决策的算法,其交互过程示意图如图2所示。

图2 DRL算法交互过程示意图
DRL算法的交互过程可以用马尔科夫决策过程(Markov Decision Process, MDP)来表示。MDP包含5个要素[S,A,p,r,γ],其中S表示状态空间,即智能体做出决策的依据信息;A表示动作空间,即智能体可以做出的决策范围;p表示状态转移概率,即在当前状态采取某一动作的情况下,下一时刻系统变为某一状态的概率;r表示回报函数,用于计算一次交互所产生的回报;γ表示折扣因子,以γ为参数对r加权累积,得到交互一个完整回合获得的总回报。DRL算法的学习过程就是通过改变在特定状态下选取不同动作的概率,以得到一种最优策略,使得一个完整回合所获得的总回报最大。
本文采用的是一种基于“行动者-评论者”(Actor-Critic, AC)框架的深度强化学习算法。AC框架包含2个DNN,分别拟合在传统RL算法中的策略函数(Actor网络)和值函数(Critic网络)。在与环境交互的过程中,智能体首先根据当前的状态和回报,更新Critic网络;再根据状态和Critic网络拟合的近似值函数,更新Actor网络,产生新的策略函数。最终,Actor网络的输出即为待求的策略。AC框架的计算流程如图3所示,相关表达式如式(15)~(19)所示。
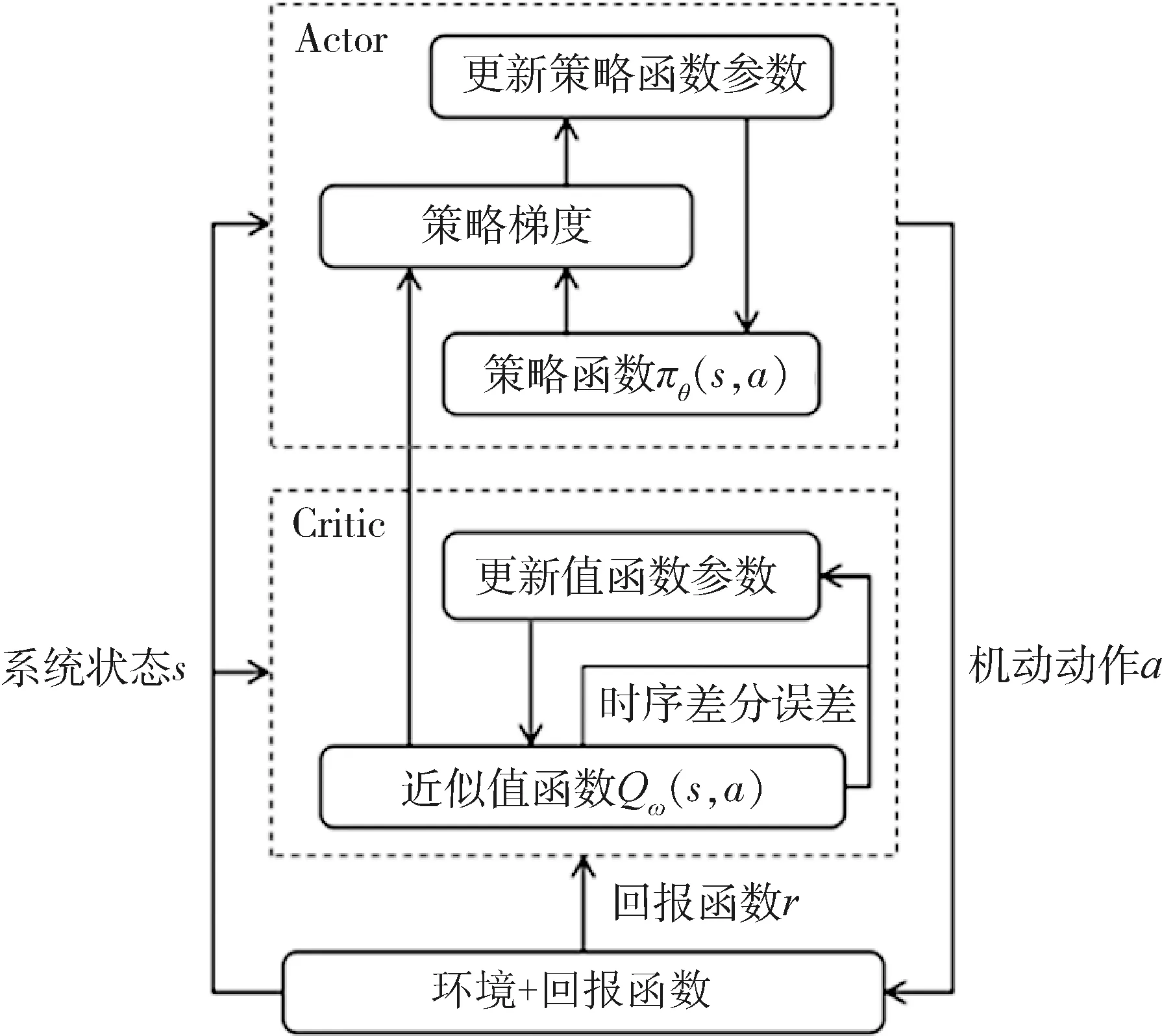
图3 AC框架的计算流程图
算法的目标函数:
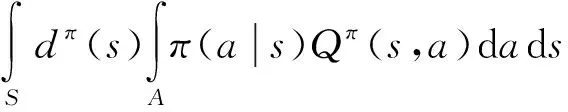
(15)
Actor网络的策略梯度:
(16)
Critic网络近似的值函数:
Qω(s,a)≈Qπ(s,a)
(17)
根据Critic网络近似的值函数计算策略梯度:
(18)
更新Actor网络的参数:
(19)
式中:J表示算法的目标函数;π表示Actor网络输出的策略,θ表示Actor网络的参数;Eπ{·}表示在策略π下的期望;dπ表示在策略π下的状态分布;Qπ表示系统在策略π下的值函数;s,a分别表示系统的状态和智能体采取的动作,S,A分别表示系统的状态空间和动作空间;Qω表示Critic网络拟合的值函数,ω表示Critic网络的参数;ε表示参数更新的学习率。
经过AC框架的计算,算法最终得到的策略具有如下形式:
Y=tanh(B3+(W23)T·tanh(B2+(W12)T·
tanh(B1+(W01)T·X)))
(20)
式中,X,Y分别表示输入的状态和输出的动作;tanh为双曲正切函数;Wij和Bj分别为权重矩阵和偏置矢量,即为前述Actor网络的参数θ,其中i,j为Actor网络的层数序号。
2.2 马尔科夫决策过程设计
采用DRL方法研究突防制导问题,需要将问题转换为MDP形式。MDP的设计至关重要,直接影响DRL算法的最终效果。
2.2.1 状态空间S
状态是DRL算法产生决策的依据,也是AC框架中两个DNN的输入。状态空间应当全面、合理地反映出所交互的环境信息,避免不必要的信息干扰。本文为了避免先验知识的干扰,没有选用传统导引律所依据的角度信息,而是选用了突防拦截双方原始的位置和速度作为状态。
S:〈x,y,z,vx,vy,vz〉
(21)
2.2.2 动作空间A
DRL算法作为决策的控制量称为动作,其取值范围由动作空间表示。本文选用在基准坐标系中的需用过载作为动作。
A:〈NCx,NCy,NCz〉
(22)
当需用过载输出到环境(仿真程序)中以后,通过式(10)转换到箭体系并舍弃X轴方向的分量,再通过式(11)~(12)求得角度指令。
2.2.3 状态转移概率p
状态转移概率p表征了环境的交互规则,在突防拦截问题中主要为双方轨迹积分所用的动力学规律。在本文选用的DRL方法中,状态转移概率p不通过解析表达式给出,而是包含在Critic网络所拟合的关系中,在交互过程中自行更新。
2.2.4 回报函数r和折扣因子γ
回报函数应当设计得形式简单,易于使算法获得优化的方向。本文将回报函数设计为2部分之和:1)过程回报,每步都有值;2)终点回报,只在回合的最后一拍才有值。为了避免先验知识的干扰,本文只选用双方斜距构建回报函数,最后一拍的双方斜距就是交会摆脱量,也就是算法最优化的目标。
本文将过程回报rt设置为当前的双方斜距dt与前一刻的双方斜距dt-1之差,如式(23)所示。将终点状态分为“被拦截”和“成功突防”两类,将终点回报rend设置为摆脱量dend与常系数k1的积再加上偏置常数k,其中2类结果对应的偏置常数取值分别为k2和k3,如式(24)所示。这样设置使得不同结果获得的总回报有区分度,便于导向期望的结果。
rt=dt-dt-1
(23)
(24)
而折扣因子γ用于对回报函数加权累积以得到一个回合的总回报,进而计算策略梯度。折扣因子γ的取值范围为[0,1],用于调整距离初始步较远的回报的重要程度。由于本文关心的是最终的交会摆脱量,而不关心每一步的双方斜距,因而将折扣因子γ设置为1。
最终得到每个回合的总回报R如下:
(25)
式中,Tn表示该回合的总交互步数。
可以看出,算法的总回报就是最终的交会摆脱量与初始双方斜距的线性和。这样设置使得算法每次交互都可以获得与最终目标相关的量,便于系统规律的拟合,同时避免了将路径计入优化的目标。
2.3 基于DRL算法的机动博弈制导律训练过程
基于DRL算法的机动博弈制导律交互过程如图4所示。图中,转换过程是指1.3.1中所述将需用过载和重力加速度统一转换到箭体系后相减。
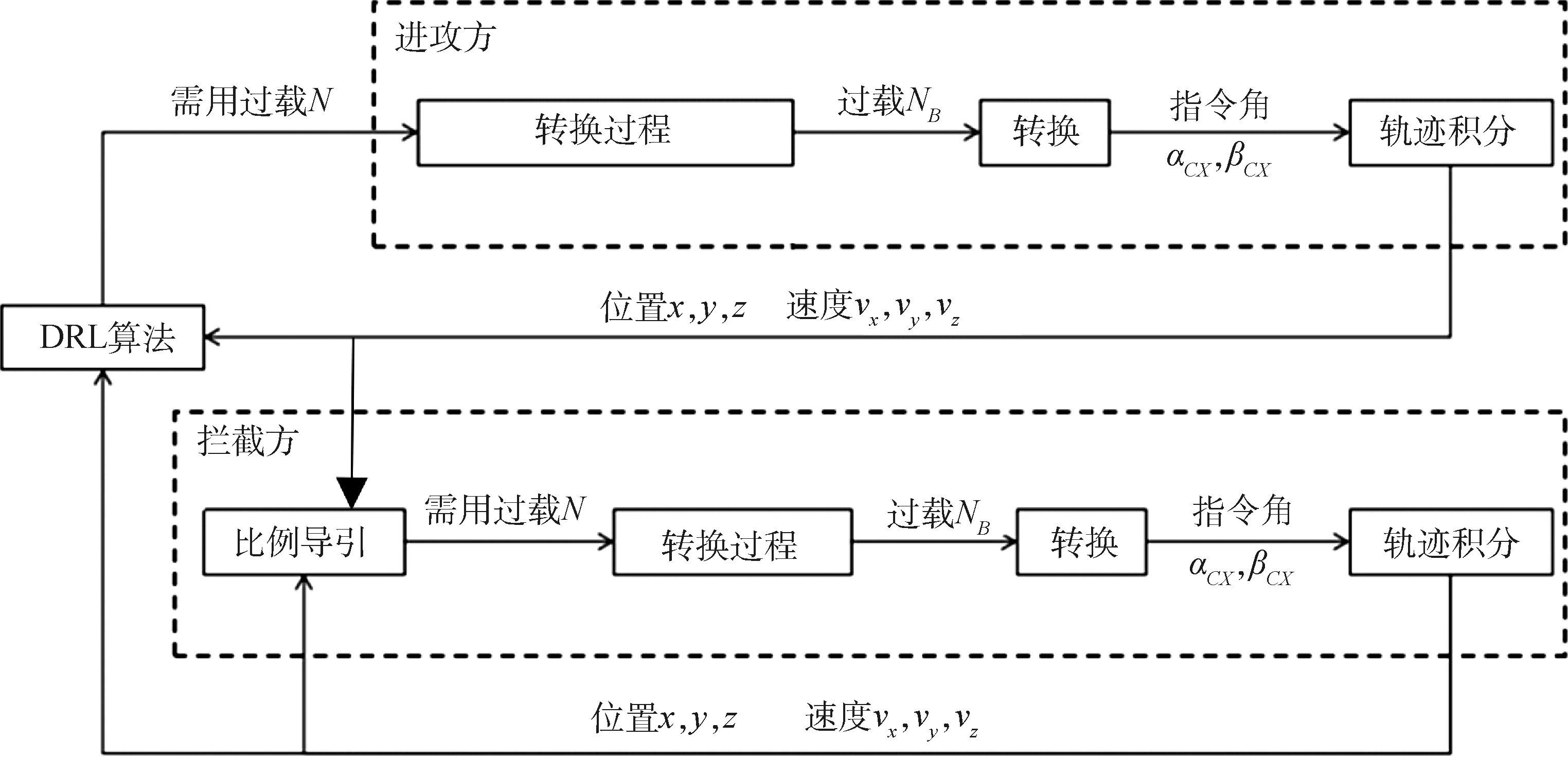
图4 基于DRL算法的机动博弈制导律交互过程
轨迹平均奖励值曲线如图5。可以看出随着交互步数的增加,平均奖励值曲线逐渐上升,最终稳定在了一个较高值,表明收敛到了一个较优的解。
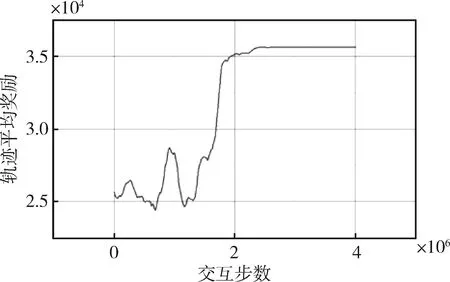
图5 轨迹平均奖励
算法直接输出的需用过载曲线如图6所示。
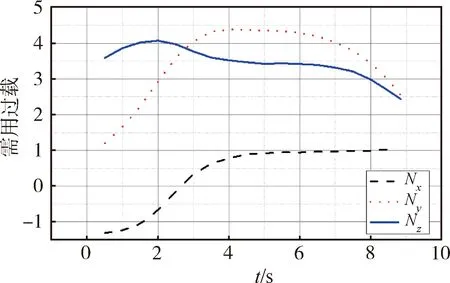
图6 需用过载曲线
3 仿真校验
3.1 实验描述
本节对三维空间内的一对一突防场景进行了仿真模拟,假设进攻方在下压点之前完成突防,所选用的进攻方和拦截方均为轴对称无动力飞行器,拦截方机动能力强于进攻方。由于目前部分反导拦截器采用破片杀伤战斗部[22-23],毁伤半径大于动能拦截器,故将双方斜距小于20m视为突防失败。作为对照,添加了不同相位的蛇形机动仿真,以模拟传统蛇形机动在不同的拦截方遭遇时间下的表现。相关设置如表1所示。

表1 仿真实验相关设置
其中,蛇形机动的制导指令生成方式为:在无机动制导指令的基础上,侧向叠加一个以正弦规律变化的过载指令。叠加正弦指令后的视线系过载如式(26)所示。
(26)
式中,所选指令相位φ为+π/4,-π/3.5,分别为仿真得到的使交会摆脱量相对较大和较小的指令相位。
3.2 实验结果与分析
图7(a)~(d)分别为无机动、2个相位的蛇形机动和采用DRL制导律机动的指令角度曲线图。图8(a)~(d)分别为4种机动下的突防轨迹图。表2列出了4种机动下的交会摆脱量和突防增加时间。
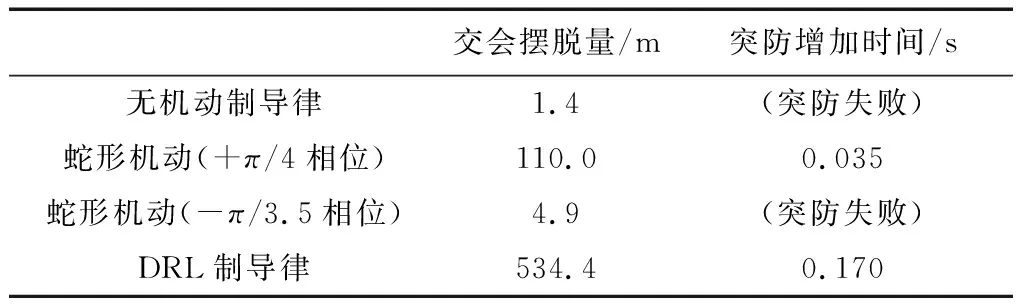
表2 交会摆脱量与突防增加时间对比
由图7(d)和图8(d)可以看出,由DRL算法得到的突防策略是根据拦截方的位置和速度方向以最大过载向某一方向进行机动。
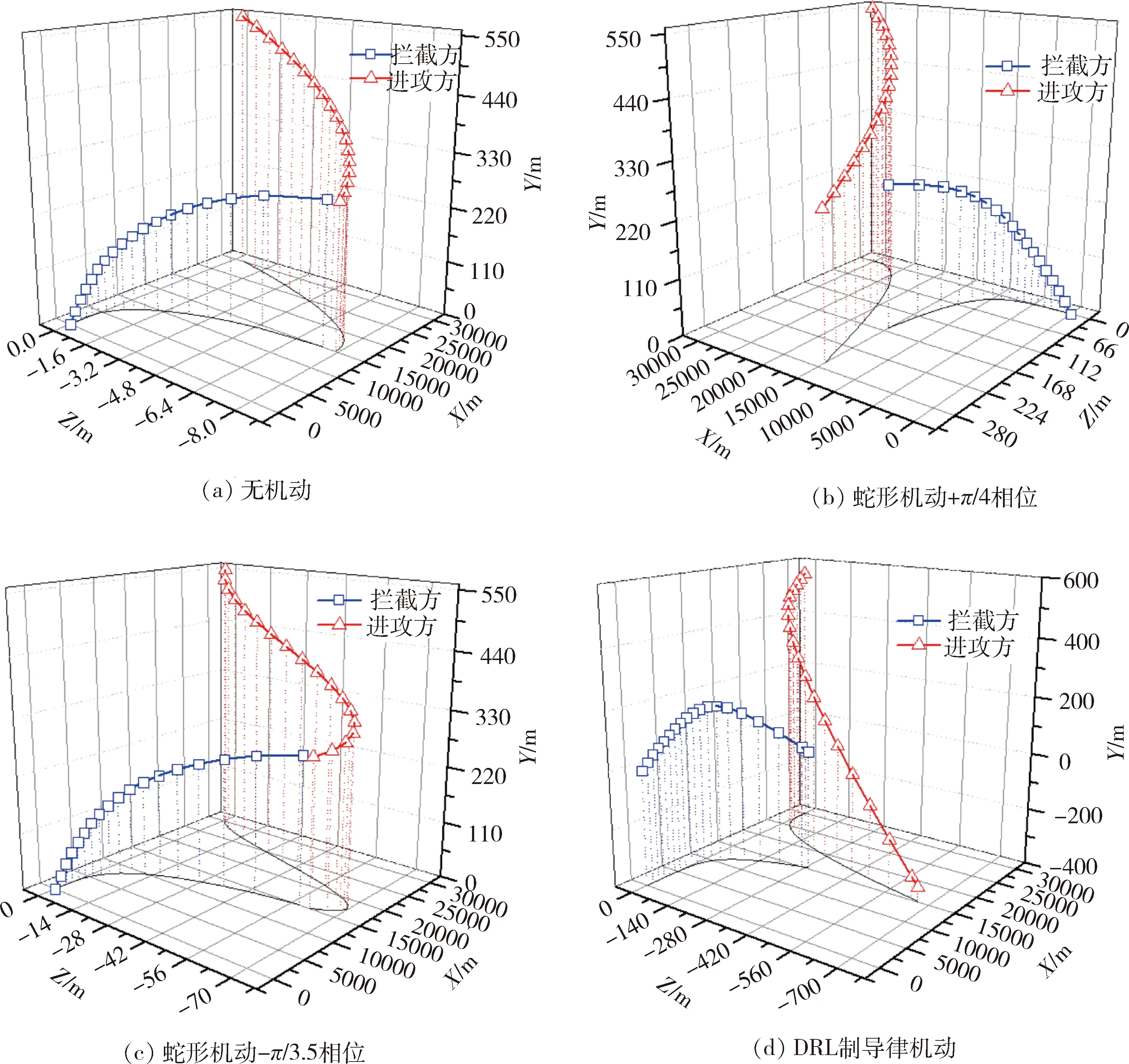
图8 突防轨迹图
由图7~8和表2可以看出,蛇形机动的交会摆脱量受机动指令相位影响较大,指令相位为-π/3.5
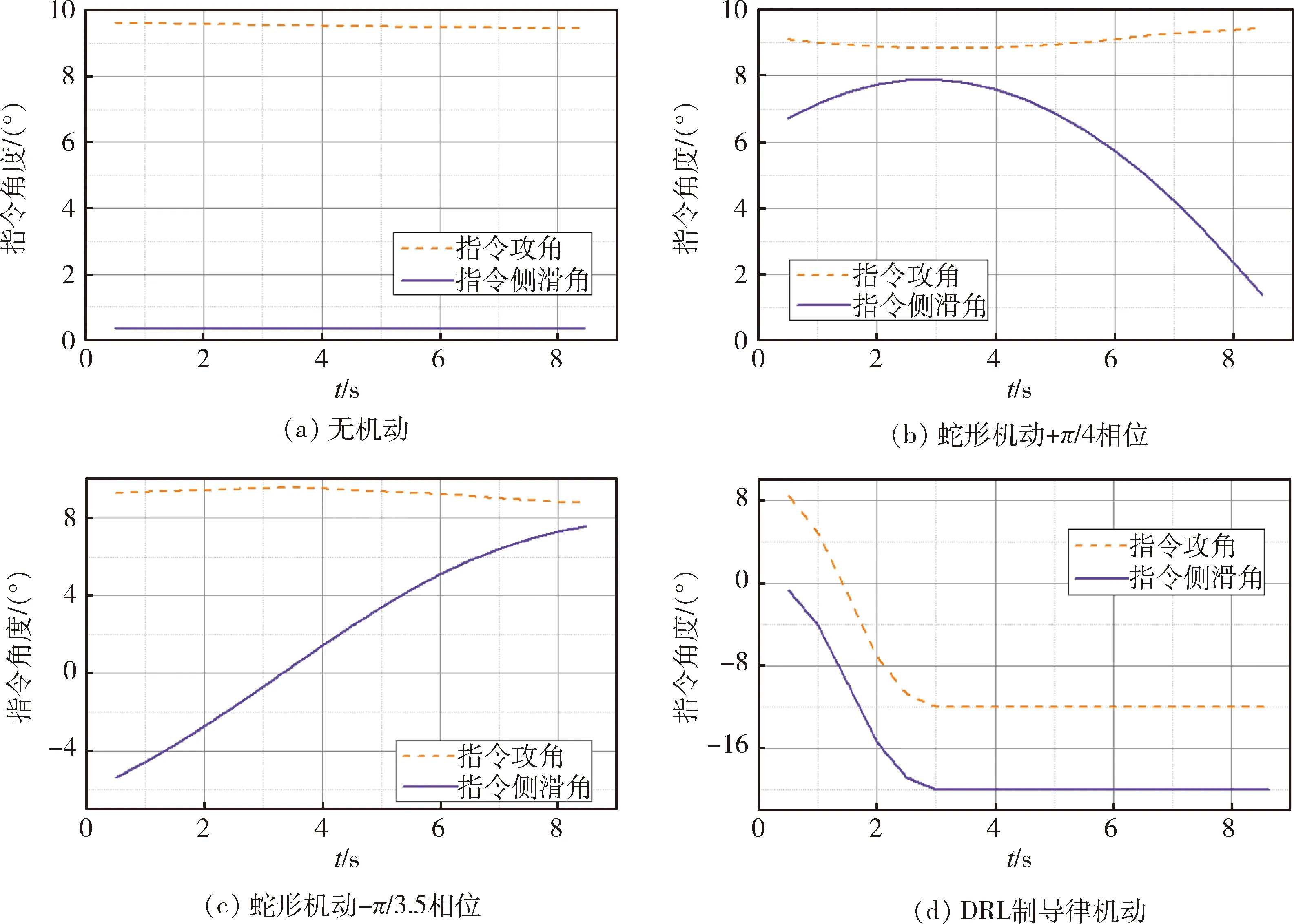
图7 指令角度曲线图
时会导致突防失败,而DRL制导律机动则不存在相位问题,突防效果较稳定。由表2可以看出,相较于蛇形机动表现较好的情况,DRL制导律机动的交会摆脱量有显著提升。
由表2还可以看出,DRL制导律机动突防所用的时间比蛇形机动略长。因为较大机动量的飞行轨迹较长,所以在速度接近的情况下,用时会较长。
在突防完成后,将采用DRL制导律机动的进攻方的制导律切换回平飞基础制导律,继续完成进攻轨迹,得到在击中目标点处的落速损失约为14.5%,尚在可以接受的范围内。因而,在只进行一次突防机动的情况下,DRL制导律机动不会对后续打击任务产生太大影响。
4 结论
提出了一种基于DRL算法的机动博弈制导律。在能获取拦截方位置和速度信息的情况下,该机动博弈制导律能够根据信息自主决策,产生合适的制导指令完成突防。经仿真验证表明,相较蛇形机动而言,该机动博弈制导律能够显著提升交会摆脱量,且突防效果较稳定。

