一种带有观测器的飞行器性能预设控制方法*
张 远 黄万伟 田 灿
1. 北京航天自动控制研究所,北京 100854 2. 宇航智能控制技术国家级重点实验室,北京 100854
0 引言
高超声速飞行器(Hypersonic Flight Vehicle, HFV)指的是一类飞行马赫数大于5的飞行器,其航程远、速度快,可实现低成本天地往返,具有广阔的军用和民用前景[1]。由于系统表现为强非线性、快时变性的动力学特性,同时气动参数、机体参数存在大范围摄动,对姿态控制提出了更高的要求和挑战,成为近年来控制领域研究的重点之一。
近年来,学者们开展了诸多HFV控制系统的设计与研究,形成了一系列典型的控制方案架构。其中,反步法简化了针对高阶非线性系统直接设计控制器的难度,成为研究重点之一,其核心思想是将高阶非线性系统控制问题分解为多个不超过系统阶次的子系统,递归设计Lyapunov保证子系统逐步稳定,最后获得整个系统的Lyapunov稳定,实现指令的跟踪控制。文献[2]通过设计一种滑模微分器估计虚拟指令的微分信号,缓解“计算膨胀”情况,同时研究了攻角非对称时变约束控制;文献[3]进一步关注工程中的航迹倾角难测量的应用难点,用高度和速度测量值以及高阶微分器设计了航迹倾角在线估计方法,基于反步法设计航迹倾角子系统控制器,同时引入辅助系统降低执行机构饱合带来的负面影响;文献[4]则提出基于高阶跟踪微分器的减步控制方案,利用其对给定信号任意阶导数精确估计的能力,减少设计步骤,再结合扩张状态观测器(ESO, Extended State Observer)获得综合扰动值,用于补偿控制;文献[5]针对HFV的纵向模型,将其分为速度和高度子系统,且把虚拟控制律设计中需要的导数作为不确定的一部分,设计自适应律应对含有未知上界的不确定性,避免了指令求导,实现速度和高度的精确跟踪。
然而,上述的控制方案可以保证系统以指数形式收敛,没有考虑控制系统的暂态性能和稳态性能(如超调、收敛时间、问题误差),如果可根据预先设计的约束条件使得系统收敛时间可调、稳态精度可控,则具有较强的工程意义。因而,近年来能够满足这一需求的性能预设控制(PPC, Prescribed Performance Control)得到了学者们的广泛关注[6-9]。文献[6]针对弹性HFV的高度和速度通道设计指数型性能预设函数;文献[7]研究了一种适应误差初值未知的性能预设控制方法,利用神经网络反演控制和最小参数方法,针对纵向模型子系统设计性能预设控制器;文献[8]分别针对速度子系统和高度系统设计PI和反步法性能预设控制器,用单隐层神经网络逼近系统不确定性;文献[9]则在对存在执行故障的建模基础上,设计基于有限时间衰减的预设性能函数,采用反步法设计有限时间性能预设控制器。
基于上述文献的启发,本文旨在针对HFV的纵向姿态通道,设计一种时间可设定的性能预设控制方案,并通过数值仿真校验了该方案在存在复合时变干扰情况下的控制性能,主要贡献如下:
1)提出一种时间可设定新型预设性能函数,在此基础上设计基于反步法的性能预设控制律,能够保证在设定时间内保证跟踪误差收敛至设定约束域,且收敛速度可根据需求灵活调节;
2)设计有限时间收敛扩张状态观测器,相对于传统扩张状态观测器,可保证其更快的收敛速度,保证系统的控制精度;
3)因反步法需要指令微分项存在的“计算膨胀”情况,引入一种改进的跟踪微分器缓解该问题。
1 问题描述
1.1 模型说明
考虑工作在水平无侧滑状态时的HFV,侧滑角β和倾侧角μ都为0,纵向和横侧向可相互解耦,则HFV模型可简化为式(1)所示[10]。
(1)



(2)
其中,Δα和ΔQ表示包含参数摄动和外界时变干扰的集总扰动。将式(2)写成形如式(3):
(3)
1.2 控制目标
由1.1节中的带有集总扰动的模型可知,HFV在飞行过程中经历大包线飞行,其飞行环境及机体参数都将出现大范围摄动,对于控制性能提出较大的挑战。因此,若存在持续性扰动,则无法保证暂态控制精度,稳态精度也无法持续满足。若以攻角为例,将其跟踪误差进行暂态性能和稳态性能两方面的精确约束,则可达到时变扰动下的高精度控制需求。可定义攻角的跟踪误差预设性能条件如下:
-δαLρfα(t)
(4)
其中,ρfα(t)为攻角跟踪误差的性能预设函数,其约束了期望的暂态性能(如收敛速度、最大超调)和稳态性能(如跟踪稳态误差)。δαU和δαL分别为设定的误差上、下界,满足δαU,δαL∈(0,1]。
本文的主要控制目标为:1)系统输出攻角α能够精确跟踪给定的时变攻角指令αc;2)在存在时变集总干扰的情况下,暂态响应满足设计需求,稳态误差在预先设定的范围之内。
2 新型性能预设反步控制器
本节针对纵向姿态系统设计新型性能预设控制器,主要由4部分构成:1)针对攻角子系统和角速度子系统引入性能预设函数,并对受约束的跟踪误差进行无约束转换;2)利用反步法进行姿态系统控制器设计;3)针对反步控制律中用到的指令微分项,引入跟踪微分器;4)针对集总扰动,设计有限时间扩张状态观测器,获得扰动和状态量,用于控制律设计。完整结构框图如图1所示。

图1 HFV纵向姿态模型新型性能预设反步控制器结构
2.1 性能预设函数及误差转换
一般地,对于性能预设控制而言,第一环节是设计性PPC,其定义如下:
定义1[11]:连续函数ρ(t):+→+为性能预设函数,且满足如下2个条件:
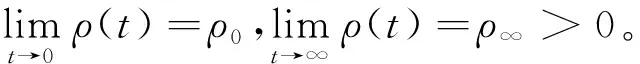
常见的PPC主要包含指数型、正切型和倒数型,如式(5)~(7),均可满足定义1条件。
ρ(t)=(ρ0-ρ∞)exp(-kρt)+ρ∞
(5)
ρ(t)=coth(ρ0+kρt)-1+ρ∞
(6)
(7)
其中,ρ0>0,ρ∞>0,kρ>0为待设计参数,ρ0代表初始误差上界,ρ∞代表稳态精度的约束,kρ代表衰减速率,直接影响系统的暂态性能。
根据定义1,本节设计一种有限时间性能预设函数来满足指令跟踪误差的暂态响应和稳态性能,如式(8)。
ρi(t)=
(8)
其中,i=α,Q代表内外环的性能预设函数,且ρi0≥1,ρi∞>0为待设定参数,Ti为设定时间值。相比于传统PPC,本文设计的性能函数能够在设定时间点满足收敛要求,且灵活可调整。
为满足跟踪误差预设性能需求式(4),需要进一步将跟踪误差转化为等价无约束形式:
e(t)=ρ(t)S(ε(t))
(9)
其中,ε(t)为转换误差,S(ε(t))为光滑递增转换函数,其满足如下条件
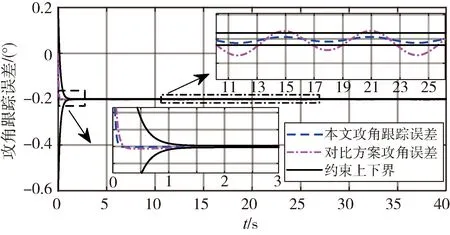
1)-δiL 则可引入指数型转换函数 (10) 由于S(ε(t))严格递增,转换误差可以通过反函数求解为: (11) 其中λi=ei(t)/ρi(t),i=α,Q。 本文基于反步法思想将系统(3)的控制系统设计分为姿态环虚拟控制律设计和角速度环真实控制律设计2个步骤。 步骤1:设计姿态环虚拟控制律 选择姿态角系统的李雅普诺夫函数 (12) 对式(12)求导 (13) (14) 将式(14)代入到式(13),则有 (15) 步骤2:设计角速度环控制律 选择姿态角速度系统的李雅普诺夫函数 (16) 对式(16)求导 (17) (18) 将式(18)代入式(17),则有 γQVQ+Ωα+ΩQ≤-γαVα-γQVQ≤0 (19) 由此可得,闭环系统是稳定的。 由式(14)以及式(18)的形式可知,控制律的设计中需要用到指令的微分量,为了防止“计算膨胀”问题,引入跟踪微分器。受到滑模理论的启发,引入终端因子来抑制高频震颤,设计基于Sigmoid函数的微分跟踪器[12],其形式如式(20)。 (20) 其中tansig(x)=2/(1+exp(-2x))-1,v(t)是输入信号,x1(t)是跟踪信号,x2(t)是微分信号,k,λ,l1,l2,p是待设定参数,k=30,λ=10,l1=10,l2=15,p=0.8。 对于性能预设控制器的设计而言,其对于集总扰动的估计精度要求较高,受文献[13]启发,设计一种有限时间扩张状态观测器,用于对内外环集总扰动的估计。考虑带有不确定系统 (21) (22) 则针对姿态系统而言,以姿态角系统为例可设计如式(23)的有限时间扩张状态观测器。 (23) (24) 角速度环系统扩张状态观测器具有相同结构,且限于篇幅,这里不再赘述,稳定性证明略。至此,带有有限时间扩张状态观测器和有限时间跟踪微分器的高超飞行器纵向姿态性能预设控制器设计完毕。 本节将针对系统式(3),采用控制律式(14)、(18),微分跟踪器式(20)、不确定估计式(23)进行仿真校验与分析。验证飞行器在大攻角再入飞行过程中,存在参数摄动和持续性时变外界干扰的情况下,攻角指令的跟踪情况。针对攻角子系统和角速度子系统分别设计性能预设函数: (25) ρα0=1,ρα∞=0.005,Tα=1。 (26) ρQ0=2,ρQ∞=0.01,TQ=1。 为校验本文提出控制方案的有效性,将本文设计的控制律和传统的反步法控制律(27)对比仿真。 (27) 本文控制器及状态观测器参数见表1。 表1 控制器参数 在验证中,飞行器的不确定性模型及外界持续性扰动设置如下。 对于执行机构而言,通常可用二阶惯性环节描述执行机构模型,如式(28),且舵偏约束满足|δe|≤30°。 (28) 其中,仿真中Tδ=0.1,ωn=1。 将传统反步法和本文提出的带有性能预设的控制方案进行对比,图2为两种控制方案在表2参数偏差和时变扰动的情况下的质量跟踪响应曲线,图3为两种方案的跟踪误差曲线。由图2~3可知,两种方案均能够较好地跟踪姿态指令,但是在暂态性能(收敛时间)和稳态性能(稳态误差)上,本文的有限时间性能预设方案表现的更为优异,特别是在稳态精度方面,始终保持在约束的范围之内,相比于传统反步法,由于时变扰动的影响,其跟踪误差超出了期望的性能边界(±0.005°)。图4表示俯仰角度跟踪效果,其与姿态角子系统有相似结论,这里不再赘述。 表2 飞行器不确定模型 图2 攻角指令跟踪(本文控制器与对比控制器仿真) 图3 攻角跟踪误差(本文控制器与对比控制器仿真) 图4 俯仰角速度指令跟踪(本文控制器与对比控制器仿真) 为验证本文设计的有限时间收敛扩张状态观测器(FTESO)的有效性,将其和线性扩张状态观测器(LESO)相比,以姿态环子系统为例验证两者对时变扰动的估计效果。如图5所示,本文的有限时间扩张状态观测器在收敛速度和跟踪误差上相比于线性扩张状态观测器都有较好的性能。 图5 姿态环子系统集总扰动估计 针对带有参数摄动和外界时变扰动的高超声速飞行器纵向姿态跟踪控制问题,设计了性能约束控制器。对于跟踪误差性能约束,首先设计了固定时间的性能预设函数,相比于传统的性能预设方案,其能够保证性能函数在设定的时刻收敛至稳态值,且可根据性能需求和执行机构饱和特性调整设定时刻;针对控制律设计中需要用到的指令的微分信号量,通过引入指令滤波去避免反步法中“计算膨胀”的问题;对于带有参数摄动和时变扰动的系统,为进一步提升扩张状态观测器的性能,设计了有限时间扩张状态观测器,其在收敛速度和收敛精度上相比于线性扩张状态观测器都有较大的提升。同样本文的控制方案对执行机构提出了更高的需求,因为其在初始时刻的饱和时间更长。这也是下一步继续研究的方向,即性能约束条件下的抗饱和控制问题。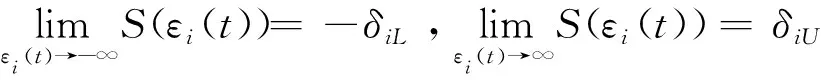
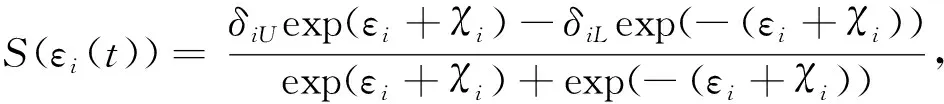
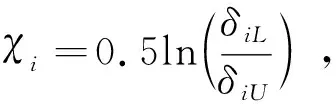
2.2 控制律设计





2.3 跟踪微分器设计
2.4 有限时间扩张状态观测器设计
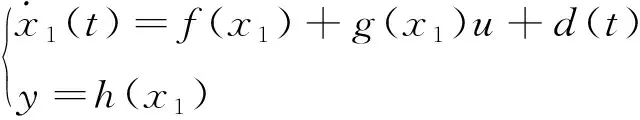

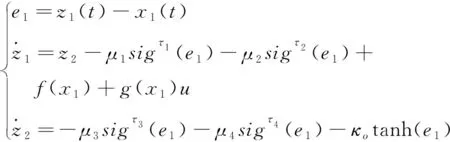


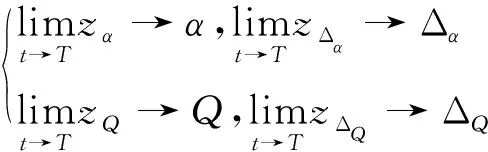
3 仿真校验

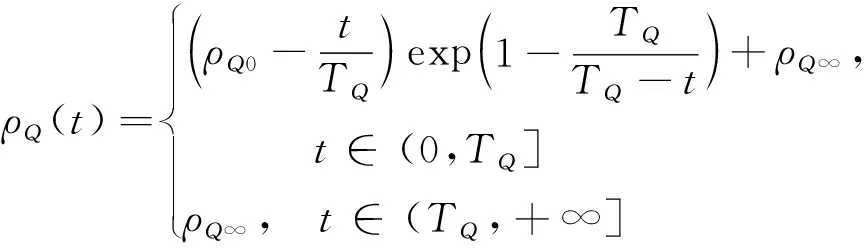





4 结论

