Multi-target ranging using an optical reservoir computing approach in the laterally coupled semiconductor lasers with self-feedback

Dong-Zhou Zhong(钟东洲)， Zhe Xu(徐喆)， Ya-Lan Hu(胡亚兰)， Ke-Ke Zhao(赵可可)， Jin-Bo Zhang(张金波)，Peng Hou(侯鹏)， Wan-An Deng(邓万安)， and Jiang-Tao Xi(习江涛)，2

1Intelligent Manufacturing Faculty，Wuyi University，Jiangmen 529020，China

2School of Electrical，Computer，Telecommunications Engineering，University of WollongGong，2522，Australia

Keywords: coupled semiconductor lasers，lidar ranging，optical reservoir computing，chaos synchronization

1. Introduction

The chaotic lidar is a lidar system utilizing the nonlinear dynamics of semiconductor lasers.[1–3]A chaotic lidar can be used as an enabling technology for many applications， such as artificial intelligence，precision range finding，object tracking and locating，through-wall detection，driverless navigation system and so on.[4–7，13–19]Among other applications，chaotic lidar ranging (CLR) has attracted considerable attention due to its advantages over short-pulse and continuous wave(CW)lidar ranging， such as low probability of intercept， high resolution in ranging and velocity，strong anti-interference ability，easy generation and low cost.[1–3，8]

There are mainly two ways for the implementation of CLRs. The first one is based on the computation of the cross-correlation between the reflected return signal and the replica of the signal transmitted.[1–9，15，16]Such correlationbased methods take advantage of the broad bandwidth of the chaotic laser and can achieve resolution up to centimeter-level.Although progress was made to increase the resolution[4–9]in recent years， further improvement becomes very difficult due to the limit of the correlation and the interference of spontaneous emission noise and channel noise. Another way of implementing CRLs is with a synchronized chaotic lidar. A synchronization chaotic lidar system has two chaotic lasers:one called the drive laser， used to generate the probe signal，and the other referred to as response laser that is used to synchronize with the drive laser. In order to probe the target，the drive laser output is modulated with a microwave signal. The chaotic probe signal with a microwave signal is reflected by the target， then delayed， finally synchronized with a chaotic signal from the response laser output. The delayed microwave signal is decoded by using high-quality chaotic synchronization. The delay time in the microwave is extracted by using Hilbert transform. The distance of the target at an arbitrary position can be calculated by using delay time. In contrast to a cross-correlation-based chaotic lidar， synchronized chaotic lidars has the potential to provide improved ranging performance in accuracy and anti-noise ability since the quality of synchronization is very robust to noise.[18–20]

The accuracy of the target ranging associated with synchronized chaotic lidar systems heavily depends on the quality and stability of chaotic synchronization. However，all existing techniques for completing chaos synchronization rely on the assumptions that the drive and the response laser systems are identical，i.e.，the rate-equations describing the two lasers must be the same and known a priori.[21–23]However，these assumptions do not hold in practice，as an inevitable mismatch always exists between the driving and response lasers.

In recent years， reservoir computing (RC) has been proven to be an effective approach in the prediction of chaotic systems from data.[24–27]The delay-based RC first proposed by Appeltantet al.，[28]composed of a nonlinear node and a delay feedback loop， is proved to be an effective and simple hardware implementation for neural network computing in hardware.[29–38]Many hardware implementations of such delay-based RC have been reported in literature， such as the electronic system，[29，30]opto-electronic system，[31，32]all-optical system，[33–35]and laser dynamical system.[36–38]Among these techniques，the delay-based RC using nonlinear semiconductor lasers has the advantages of fast-speed， high efficiency and parallel computing capability for many benchmark tasks，[33–48]such as time series prediction，[39–43]optical packet header recognition，[44]speech recognition，[45]nonlinear channel equalization[46]and so on. A growing number of studies have shown that a well-trained reservoir computer can be well synchronized with its learned chaotic system by using a delay-based RC approach.[24–27]For example， in 2017，Anoniket al.proved experimentally that a reservoir can be trained to yield similar dynamics to its learned chaotic system (similar spectrum， Lyapunov index， etc).[47]Our previous work further shows that high-quality chaotic synchronization between the driving laser array and its trained reservoir in the existence of mismatch between their rate equations can be achieved by using a delay-based optical reservoir computing approach.[42]

The 1-D lateral laser array(laterally coupled semiconductor lasers)with rich chaos dynamics represents an ideal candidate of an integrated chaotic light source，which has potential applications in multi-target chaotic lidar synchronous ranging.Compared with the multi-target ranging based on three uncoupled semiconductor lasers，the ranging to multi-target based on the 1-D lateral laser array are advantageous by a simple structure and thus there is easy fabrication on a single chip. For the application for the multi-target ranging using the 1-D lateral laser array， it is necessary to overcome the limitations of traditional optical chaos synchronization theory as described above.[21–23]The delay-based RC technology in training optical chaos synchronization provides a possible solution for this problem.[42]The stable and high-accuracy ranging to the multi-target can be achieved in the delay-based optical reservoir computing system based on the 1-D lateral laser array，owing to the realization of stable and high-quality chaos synchronization by the predictive learning，even if the existences of parameter mismatches between the driving laser element and its trained reservoir.

Motivated by these described above， in this paper， as shown in Fig. 1， we propose three parallel delay-based optical chaotic RCs using laterally coupled semiconductor lasers both subject to self-feedback and optical injection， where the light injected into each laser is modulated by a delayed reflection probe signal from a target. These RCs can be described by the coupled wave theory developed by our previous work.[48]Based on these three-parallel delay-based RCs and Hilbert phase transformation principle，we further propose a novel scheme for multi-channel synchronized chaotic lidar ranging for multiple targets. For this scheme，we demonstrate the quality and stability of the lag chaos synchronization between a well-trained reservoir computer and its learned delay probe signal with a microwave signal. We explore the influences of the delay-time of RC and the interval of the virtual nodes on the training errors. Finally， we discuss the accuracies and the relative errors of the multi-target ranging.

2. Experimental setup and theoretical method

2.1. Experimental setup

Figure 1 depicts a schematic diagram of synchronized chaotic lidar ranging for multi-targets by using three parallel delay-based RCs. Here， TLC-SL represents three laterally coupled semiconductor lasers，also referred to as a threeelement laser array. The TLC-SL1and TLC-SL2are the driving and response laser arrays， respectively. They both have three identical laser waveguides (LWGs) of width 2a， which are edge-to-edge separated 2d. The LWG A locates between the LWG B and the LWG C. The LWGs A， B， and C in the TLC-SL1are also denoted as lasers A1， B1and C1， respectively， and those in the TLC-SL2are also called as lasers A2，B2， and C2， respectively. The three driving laser elements in the TLC-SL1are chaotic radar sources to be learned for their synchronizations. With both delay-time feedback and optical injection，the three response laser elements in the TLC-SL2are utilized as nonlinear nodes to realize three-parallel delay RCs.The six neutral density filters(NDFs)are used to control light strength.The variable attenuators(VAs)are used to control the feedback strengths. The optical isolators (ISs) are applied to avoid light feedback.The AM1，AM2，and AM3are amplitude modulators.mA，mBandmCare the sinusoidal microwave signals. The fiber beam splitters (FBSs) (s=1–3) separate the output light into the photodetector and the input layer，respectively. The FBS4divides the external light from the driving semiconductor laser (D-SL) into three identical components，which are respectively injected into three phase modulations(PM1，PM2and PM3).

The system presented by Fig. 1 is composed of the transmitting module (TM)， multi-target detection module(MTDM)， three input layers， three parallel reservoirs， three output layers and ranging calculation modules(RCMs). In the TM and MTDM， three beams of chaotic light waves are respectively emitted by lasers A1，B1and C1with self-feedback，and they are respectively modulated withmA，mB，andmC(sinusoidal microwave signals)using amplitude modulators，and these amplitude-modulated chaotic light waveforms are called the probe signals，such as PS-A，PS-B，and PS-C.These three probe signals are transmitted to by the optical transmitting antennas(OTA1–3)，then reflected by the three targets and back to the optical receiving antennas(ORAs).Note that the signals collected by the receiving antennas can be considered as a delayed version of the three probe signals，which are denoted asuA(t-τA)，uB(t-τB)anduC(t-τC).

Fig.1. Schematic diagram of synchronized chaotic lidar ranging for the multi-target by utilizing three parallel delay-based optical reservoir computers using three laterally coupled semiconductor lasers(see texts for the detailed description).

2.2. Theoretical method

The nonlinear dynamics of the three laser-elements in the TCL-SL1with self-feedback can be described by the coupled mode theory developed by our previous work presented in Ref.[48]as follows:

In the reservoir layers， the dynamics of the three laserelements in the TCL-SL2with both delay-time feedback and optical injection can be modeled as

whereEdis the amplitude of CW output from the D-SL;cis the speed of light in vacuum;n0is the refractive index of the laser waveguides A， B， and C in the TCL-SL2. Thej-th masked input signalSj(t)is multiplied by thej-th input datauj(n′j)， the mask signal， thej-th modulated signal and the scaling factorγ，which can be expressed as

where the term Mask is chaos signal and presented in Ref. [49]. In these three input data，kA=τA/h，kB=τB/h，andkC=τC/h.his the step size.τAis the channel delay between the TA1and RA1.τBis that between the TA2and RA2.τCis that between the TA3and RA3.

whereωjis the angular frequency of thej-th microwave signal;andAis the amplitude.By using the synchronous division presented in Fig. 1， these three-channel decoding microwave signals can be obtained by

Under three lag synchronization solutions(see Eq.(22))，these decoding microwave signals are derived from Eqs.(25)and(26)as follows:

According to Hilbert transform， the analytic signal ofmj(t)is written as

and the distance of these three targets can be derived as

wherecis the speed of light in vacuum.

3. Results and discussion

We calculate numerically Eqs.(1)–(14)by using the fourorder Runge–Kutta method with a stephof 1 ps. For the numerically solving Eqs.(1)–(7)for the TCL-SL1，6000 samples of input data are recorded under the sampling interval of 10 ps.After discarding the first 1000 samples(to eliminate transient states)，we use the 3000 points for training the three reservoirs(RA，RB，and RC)，and take their remaining 2000 points to test these reservoirs. Moreover，three mask signals are all chaotic signals generated by two mutually-coupled SLs， as presented in Ref.[49].The intervals of these mask signals are all denoted byθand set to 20 ps. The amplitudes of the mask signals are adjusted， making their standard deviations to be 1 and mean values of 0. The periodTof the input data is set as 8 ns，and hence the data processing speed is 125 Mb/s. The number of virtual nodesNis considered as 400， whereN=T/θ. The delay timeτ2=T+θ. The scaling factorγis set as 1.

For the prediction tasks of the nonlinear dynamics of the lasers A1，B1，and C1，the training error，i.e.，thej-th normalized mean-square error(NMSEj)between thej-th input data(uj(n-kj))and thej-th reservoir(Rj)outputyj(n)，is calculated to measure the performance of the Rj， which is defined as

whereLis the total number of data in the testing data set;the term var represents the variance. The NMSE with subscripts ofjindicates how far the time seriesyj(n) generated by thej-th reservoir (Rj) deviates from thej-th delayed time seriesuj(n′j). NMSEj= 0 means thatyj(n) is perfectly matched withuj(n′j). When NMSEj=1 indicates that they are no similarities at all. Moreover， while NMSEjis less than 0.1， the trained reservoirs(RA，RBand RC)can infer the output chaotic trajectories from the lasers A1， B1， and C1， respectively. In other words，thej-th delayed input time seriesuj(n′j)from the laser-jelement in the TCL-SL1wishes to synchronize with the trained predicted valuesyj(n) from the Rjoutput， which can be characterized by using the correlation coefficient as follows:

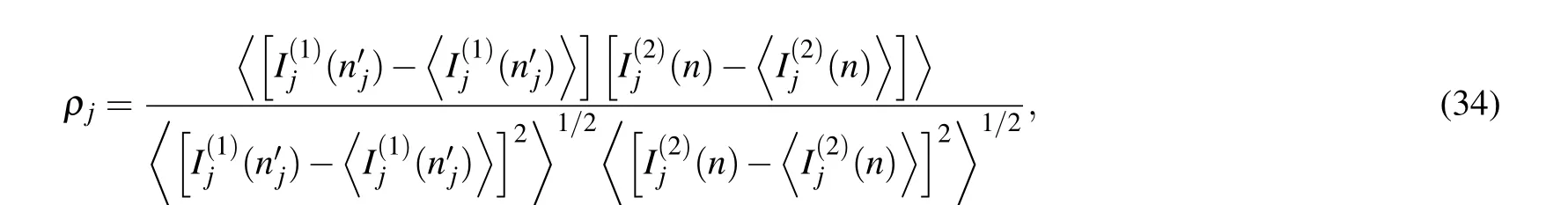
3.1. Training errors for the chaotic dynamics

To further explore the predictive performances of three parallel trained reservoirs to the chaotic trajectories of threechannel delayed probe signals. Figure 3 displays three training errors(NMSEA，NMSEBand NMSEC)as a function of the delay-timeτ2underθ=20 ps，τA=10 ns，τB=15 ns， andτC=20 ns. It can be clearly seen from Fig.3 that in the region ofτ2between 1 ns and 10 ns，these training errors are less than 0.065， but they show a rise in oscillation with the increase ofτ2. The reason that a longer delay-timeτ2results in an oscillation rising training error may be explained as follows. In this work，whenθis fixed at 20 ps，T=τ2-θandN=τ2/θ-1，a largerNis accompanied by a largerτ2，indicating that a higher dimension state space. In such a case， the predictions of the trained reservoirs to the delayed probe signals becomes unstable and more difficult，resulting in a larger NMSE. Moreover，for the prediction of three-channel delayed probe signals，figure 4 shows their training errors as a function of the virtual node intervalθ. One sees from this figure that withTfixed at 8 ns，these three training errors appear in a cliff-like decline whenθincreases from 4 ps to 12 ps，then gradually stabilize to 0.0474 with the increase ofθfrom 12 ps to 200 ps. The reason is explained as follows: a smallθinduces to the reduction of the trained reservoirs response，showing larger training errors. Asθincreases from 15 ps to 200 ps， the response of the trained reservoir will be further enhanced， resulting in less training errors. In addition，although the dimension of the state space further decreases with the increase ofθ， there are still enough virtual nodes for training reservoir，making these training errors small and varied between 0.0474 and 0.055.

Fig.3. (a)The NMSEA as a function of the delay-time τ2 for the prediction of the trained reservoir RA to uA(n′A); (b)the NMSEB as a function of τ2 for the prediction of the trained reservoir RB to uB(n′B);(c)the NMSEC as a function of τ2 for the prediction of the reservoir RC to uC(n′C). Here，τA =10 ns;τB=15 ns;τC=20 ns and other parameters except for τ2 are the same as those in Fig.2.

Fig.4. (a)The NMSEA as a function of the virtual node interval θ for the prediction of the trained reservoir RA to uA(n′A);(b)the NMSEB as a function of θ for the prediction of the trained reservoir RB to uB(n′B);(c)the NMSEC as a function of θ for the prediction of the reservoir RC to uC(n′C). Here，τA=10 ns;τB=15 ns;τC=20 ns and other parameters except for θ are the same as those in Fig.2.

3.2. Predictive learning of three-channel lag chaotic synchronizations

3.3. Synchronized chaotic lidar ranging to multi-target

Fig.7. (a)Time traces of the phases φmA and φ′mA;(b)those of the phases φmB and φ′mB;and(c)those of the phases. Here，τA=10 ns，τB=15 ns，τC=20 ns and other parameters are the same as those in Fig.2.

Fig. 8. (a) The temporal trace of the measured distance dA for the target TA; (b) that of the measured distance dB for the target TB; and (c) that of the measured distance dC for the target TC. Here，τA=10 ns，τB=15 ns，τC=20 ns and other parameters are the same as those in Fig.2.

Fig.9. Maps of the three relative errors evolutions in the parameter space of τ and τA (τB or τC). Here，(a)REA;(b)REB;(c)REC. State 1: 0 ＜RE j ≤0.1%and dark-blue; state 2: 0.1%＜REj ≤0.2%and light-blue; state 3: 0.2%＜REj ≤0.3%and blue-green; state 4: 0.3%＜RE j ≤0.4%and green; state 5:0.4%＜RE j ≤0.6%and yellow.

Finally，the relative errors REA，REB，and RECare introduced to describe the accuracy of the target ranging as follows:

where the symbol“||”represents absolute value. We quantize these relative errors for observation. State 1: 0＜REA， REB，REC≤0.1%;state 2: 0.1%＜REA，REB，REC≤0.2%;state 3: 0.2%＜REA， REB， REC≤0.3%; state 4: 0.3%＜REA，REB，REC≤0.4%;state 5: 0.4%＜REA，REB，REC≤0.6%.Under high-quality lag chaotic synchronizations， figure 9 depicts the evolutions of these three relative errors in the parameter spaces ofτandτA，τandτB，τandτC. It is found from Fig. 9 that their relative errors are all less than 1%， and stay in state 1 in these three large parameter spaces. In addition，when the channel delaysτA，τB，andτCare all fixed at 10 ns or 16 ns，their relative errors appear an increase in a slight fluctuation and reach to 0.55%.Therefore，all relative errors of these three targets ranging are small and less than 0.6%， indicating that the ranging scheme can achieve high accuracy.

From these results observed from Figs.6–8， under highquality lag chaotic synchronization obtained by the delayedbased reservoir computing approach， the ranging to three targets has good real-time stability. Their absolute errors reach millimeter magnitude， and their relative errors are very small and less than 0.6%.

4. Conclusions

To sum up，we proposed to use a machine-learning technique by means of three parallel optical chaotic reservoirs for realizing the ranging to three targets， respectively. The system proposed consists of the driving three-element laser array with self-feedback， multi-target detection， three input layers，three parallel reservoirs， three output layers， and ranging calculation. Here，these three optical reservoir computers are implemented by the chaotic three-element laser array with both delay-time feedback and optical injection. Three-channel delayed probe signals from the driving three-element laser array with self-feedback are modeled by these three trained reservoir computers，respectively. Our findings show that any onechannel delayed probe signal can synchronize well with its corresponding trained reservoir computer. In other words，high-quality lag chaotic synchronization between them can be achieved even despite the existence of some mismatches between the key parameters of the response three-element laser array and the driving three-element laser array. In addition，the three-channel synchronized probe signals are utilized for the ranging to three targets. Our investigation results indicate that stable and real-time ranging can be achieved for three targets.

Significantly，most previous works focused on laser-based on chaotic radar ranging by using the cross-correlation between the reflected return signal and the replica of the signal transmitted.[1–9，15，16]In these works， the resolution is used to judge the accuracy of the ranging to target. Such correlationbased methods take advantage of the broad bandwidth of the chaotic laser and can achieve resolution up to centimeterlevel，indicating that the absolute errors for the ranging to target reach centimeter level. Our previous works reported in Refs.[18，19]explored another new way of implementing the ranging to target by using the synchronized chaotic lidar between driving laser and response one，where the relative errors for the ranging were obtained as less than 2.7%and 11%，respectively，based on the traditional complete chaos theory. By comparison，in this paper，based on the optical reservoir computing approach， the absolute errors for the ranging to multitarget reach millimeter level， and the corresponding relative errors are very small and less than 0.6%. Therefore， the results presented in this paper are better than those in the other reported works. Moreover，when the driving lasers and the response ones consist of four or more-element laser array， four or more-channel delayed probe signals from the driving four or more-element laser array with self-feedback can be modeled by the four or more reservoir computers implemented by the response four or more-element laser array with both delay-time feedback and optical injection，respectively. Using the reservoir computing method，any one of the four or morechannel delayed probe signals can synchronize well with its corresponding trained reservoir computer. Under this condition， the stable and real-time ranging can be realized for four or more targets.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 62075168)， GuangDong Basic and Applied Basic Research Foundation (Grant No. 2020A1515011088)， and Special Project in Key Fields of Guangdong Provincial Department of Education of China(Grant No.2020ZDZX3052 and 2019KZDZX1025).