Development of an electronic stopping power model based on deep learning and its application in ion range prediction

Xun Guo(郭寻)， Hao Wang(王浩)， Changkai Li(李长楷)，Shijun Zhao(赵仕俊)， Ke Jin(靳柯)，†， and Jianming Xue(薛建明)

1Advanced Research Institute of Multidisciplinary Science，Beijing Institute of Technology，Beijing 100081，China

2State Key Laboratory of Nuclear Physics and Technology，School of Physics，Peking University，Beijing 100871，China

3Department of Mechanical Engineering，City University of Hong Kong，Hong Kong，China

4Center for Applied Physics and Technology，Ministry of Education Key Laboratory of High Energy Density Physics Simulations，and Peking University Branch of Ministry of Education IFSA Center，Peking University，Beijing 100871，China

Keywords: electronic stopping power，deep learning，ion range，reciprocity theory

1. Introduction

In the past century， the energy loss of energetic ions in matter has been a momentous subject and garnered great attention， since it is important for both scientific research and industrial applications， including radiation damage， ion beam analysis， nuclear physics， ion implantation and nano-device modification.[1–5]Extensive experimental measurements and theoretical studies by Bethe，[6]Bloch，[7]Lindhard，[8]Sigmund，[9]and Ziegleret al.，[10]have predicted electronic stopping power(Se)with varied degrees of success.Meanwhile， many computational codes， such as SRIM[11–13]and MSTAR，[14，15]have been developed to predict these values and to simulate the ion transportation behavior in solids.Particularly， with the help of time-dependent density functional theory，[16–18]the accuracy ofSehas been significantly improved，but still require being benchmarked against suitable experimental data.[19]Therefore， most of the existing models are actually driven by big data，and this idea has been successfully applied in many engineering applications.

On the other hand，describing and predicting the stopping power of energetic ions in solid is extremely complicated:both the ion and solid properties affect the energy transfer process.Though the contribution from many factors， such as binding energy， state of matter， electron structure， band gap and excitation energy， have been suggested to be important for this process，[1，2，20–22]most of the prevalent stopping power models only consider the influence of collision parameters，including the atomic number and mass for the incident ion(Z1，M1)and target material(Z2，M2)， along with the kinetic energy of the incident ion(Ein)，[11，14，23，24]because it is almost impossible for classical methods to find an appropriate fitting function to capture the complicated relations among many parameters. Therefore，their predictive accuracies are fundamentally restricted， the reason why a new method to overcome these problems has been highly desired for many years.

Recently，with the advent of machine learning technique，it becomes possible to take the raw features from large dataset directly，and mine their deeply implicit relations automatically.Especially， deep learning (DL) algorithm， which can be considered as a more complex network with multiple processing layers to represent data with multi-levels of abstraction，[25，26]has already brought about breakthroughs in many fields of science， e.g.， planning chemical syntheses，[27]acceleration of super-resolution localization microscopy，[28–30]classifying scientific data[26，31]and solving high-dimensional problems in condensed matter systems.[32–36]Considering the large number of energy loss data obtained in the past decades， the DL based models are expected to make better use of data than those classical methods，which strongly rely on the selection of oversimplified stopping power formulas and fitting functions.

In 2020，William and Richard proposed a machine learning based stopping power model，[37]which accomplished similar calculation accuracy compared with SRIM. However， in this article， we find that the deep learning based electronic stopping power (DL-ESP) model can not only achieve high predictive accuracy: the average relative difference is about 5.7%，which is comparable to other existing classical models，but also show high accuracy in the regime that is lack of experimental data，and it would be quite valuable in many practical applications: it could provide strong support of the reciprocity theory proposed by Sigmund，[38]and give a much better prediction in evaluating the projected range of slow heavy ions in light compounds，which have been long-time challenges in this field. We believe that this model could make a major breakthrough in physics.

2. Methods

2.1. Deep learning network

To deploy DL-ESP， we used the experimental ion collision dataset collected by Paul and International Atomic Energy Agency(IAEA)，which contains nearly all the published electronic stopping power data of different ions in solids，gases and compounds，since the 1990s.[39，40]According to our tests，a 5-layer network with a grid of 16×32×64×32×16 is good enough to give the required accuracy. Our model， which includes the generating，training and invoking of neural network，is built based on the Keras[41]with the TensorFlow[42]platform as the back-end， including the generating， training and invoking of neural network. In order to balance the prediction performance forEinin both high and low energy ranges， the mean absolute percentage error(MAPE)loss function，instead of the mean absolute error(MAE)loss functions，was adopted.Moreover， we chose the rectified linear unit (ReLU) activate function[43]and the adaptive moment estimation(Adam)optimizer[44]to make the network easier to converge. We exported the fully optimized model with the smallest validate after the training process， and invoked it at the following exploration and discussion. A simple illustration of our method is shown in Fig.1.

2.2. Datasets

In this study，only 16907 experimental data of electronic stopping power (Se) for different ions， with kinetic energy(Ein) within the range of 5–1000 keV/u， were selected， since most of the experiments were carried out within this energy range. We randomly chose 13526 (80%) of them as training dataset， while the rest 3381 (20%) were used for validation.Especially，some specific experimental data，such as Ti and Kr ion in Al， were collected but excluded from the total dataset，in order to verify the predictive accuracy of DL-ESP model.

Restricted by the shortage of experimental data whenEin＜5 keV/u，especially for some heavy ions，the general predictive accuracy in the low energy range(defined as 1–10 keV/u in this study)should be enhanced in another way:by introducing some additional boundary points into the training dataset.Considering that in the energy range of 1–10 keV/u， the LSS model[8，45–47]is accurate enough to describe theSeof ion in elementary material.[48]Therefore，in this study the boundary points were generated using the LSS model expressed as

where the units ofSeandEinare 10-15eVcm2/atom and keV，respectively. Using Eq. (1)， we calculatedSeof 80 different ions， with the incident energy of 1 and 10 keV/u， in 80 types of elementary materials， and then used the boundary points only in the training dataset.

2.3. Computational detail for ion range

In order to quickly estimate the projected range (Rp) of ion in compounds in an easy way， the classical Lindhard’s equation was applied in this study， since it is a widely used and simple enough method which only containsSeandSn:[49]

Here，M1andM2are the mass of projectile(e.g.，197 for Au)and target(e.g.，20 for SiC averagely)，respectively，andRrepresents the total ion path:

whereSnandSeare the nuclear and electronic stopping power，respectively. Since DL-ESP could only provideSefor elementary materials， the electronic stopping power can be simply calculated by using Bragg’s rule:[50]

whereaandbare the atomic fractions ofAandBinABcompound system，respectively. Though there are many more advanced and accurate computational method forRp， we still chose Lindhard’s equation and Bragg’s rule in this study， because this model only contains the least factors for the stopping problem， which means that we can minimize the influence of other factors， such as binding energy and displacement threshold. Moreover， to minimize the influence of nuclear stopping power(Sn)，theSnused in this work is also calculated by SRIM，so the difference exhibited in this study only represents the contribution ofSe.

3. Results

3.1. Overall accuracy

In this study，we tookSecalculated by SRIM as a benchmark to evaluate the accuracy of this model. In addition，considering that we mainly focus on elementary materials in this work， the minimum parameters need to be considered in the calculation model areZ1，Z2andEin， because other parameters (e.g.，M1andM2) are theoretically correlated withZ1orZ2.In order to verify this deduction，we explored a simple version of DL-ESP(DL-ESP-simple)and only input the training data with the minimal information(Z1，Z2，Ein，Se)，while the standard DL-ESP has more input parameters(Z1，M1，Z2，M2，Ein，Se)，as shown in Fig.1. Also a brief comparison between SRIM and these models was explored and exhibited in Table 1，to evaluate the accuracy of DL-ESP-simple and DL-ESP.

According to Table 1， though DL-ESP has better predict accuracy than DL-ESP-simple，there is no significant difference between them， which means that deep learning can indeed mine the inline relation betweenZ1–M1andZ2–M2.Thus，it could be concluded from Table 1 that the influence of other implied parameters，such as binding energy，state of matter， electron structure， band gap and excitation energy， which are also strictly corresponding toZ1orZ2， can also be somehow revealed by the deep learning network. Theoretically speaking，DL-ESP and DL-ESP-simple would have similar accuracy if the training dataset is large enough， because nearly all of these inline relations can be captured from the big data.

Fig. 1. Schematic of DL-ESP from the atomic collision dataset and how to use it performing a highly accurate prediction. This procedure involved training data set of evaluated experimental data and boundary points.

Table 1. A brief comparison of DL-ESP and SRIM，by exhibiting the average absolute relative difference(¯σ)between predicted Se and experimental results of H，He，Li and other heavy ions，and the general consistency within 5%and 10%， which represent the percentage of absolute relative difference (|σ|) to be smaller than 5%and 10%，for the experimental data used in this work.

In order to avoid the influence of isotope，we mainly discuss the performance of DL-ESP in this study. Although DLESP can not provide an analytical expression， it can still perform highly accurate predictions，which is far more advanced than the classical methods that rely on fitting data. As shown in Table 1，the average absolute relative difference(¯σ)of DLESP is about 5.7%， very close to the performance of SRIM(4.6%)and MSTAR(about 1%–2%at high energy，but for low energy ions it increases to 10%–20%).[15]As for the general consistency within 50%and 10%，which can be defined as the percentage of experimental data whose predicted value with absolute relative difference (|σ|) smaller than 5% and 10%，SRIM and DL-ESP have similar performance， especially for incident ion heavier than He.

It should be noted that the high accuracy of SRIM is based on a series of segment fitting functions for ions with different mass and energy， so it can provide well consistence with existing experimental results. However， for the conditions that lacks the support of experiments， the accuracy of these fitting functions becomes quite controversial， since they may overlook the influence of other potential factors. Considering that the experimental data of some specific ion types or energy ranges are nearly impossible to be measured by far，either because of the limit of ion source technique or measuring difficulty， the predictive accuracy of classical fitting models can hardly been further improved，so deep learning algorithm，which can grasp a deeper sense of the complex relations hidden in the existing experimental data， is a promising way to overcome these difficulties. As illustrated previously，the difference between DL-ESP and DL-ESP-simple reveals that DL network can indeed mine the inline complex relations deeply hidden in these experimental data， which could significantly enhance the accuracy of this model. Therefore， though DLESP can hardly achieve higher overall accuracy than SRIM，its ¯σis a macroscopic evaluation of the entire dataset equally for every data point，which means that the predictive accuracy of DL-ESP is more objective than other models that are based on segment fitting functions.

3.2. Validation of predictive accuracy

To verify the predictive accuracy of DL-ESP， we calculated theSefor some experimental points which were excluded from the total dataset. Meanwhile， this model combines the advantage of the LSS model and experimental data，so it is also very important to evaluate the necessity of this treatment. Figure 2 illustrates the predictive accuracy of this model， by excluding some experimental data(Ti and Kr in Al，H in Fe and Zn)from the deep learning network intentionally，and DL-ESP can still give an accurate enough prediction with high consistency compared with both SRIM and experimental results.

Fig.2. A brief illustration of the expansion capability of DL-ESP.The electronic stopping power of(a)Ti and(b)Kr in Al，as well as H in(c)Fe and(d)Zn，calculated by using DL-ESP，SRIM and LSS model，compared with the experimental data.

It is shown in Fig.2 that although we are not sure if SRIM have used these data， both DL-ESP and SRIM can give similar prediction ofSecompared with experimental data， which means that DL-ESP can indeed predict the value ofSewith the accuracy not lower than SRIM.Moreover，compared with the entire training dataset， the amount of the hidden data is very small， so such exclusion would not observably decrease the general accuracy of this model. Moreover，the accuracy of this model could be further improved if there are more experimental data included in the dataset. More importantly，combination of the LSS model and the experimental data is very necessary， because for many ions the experimental data ofSeare not sufficient enough whenEin＜10 keV/u， meanwhile the LSS model is not applicable for high energy ion:whenEin＞100 keV/u， theSecalculated by the LSS model obviously deviated from the experimental data， as shown in Figs.2(c)and 2(d). Therefore it can be concluded from Fig.2 that the treatment of combining experimental data with the LSS model is essential and would significantly improve the predictive accuracy of DL-ESP.

3.3. A new way to support reciprocity theory

It has been a long-standing problem that the electronic stopping cross sections of some slow heavy ions are inaccurate as predicted by classical methods， in which theSe’s are obviously overestimated for heavy ions(e.g. Au)in light targets(e.g. Al)，[51，52]as illustrated in Fig.3. The abnormal highSefor Au ion in Al in Fig. 3 in the low energy range (about 140 in units of 10-15eV·cm2/atom whenEin≈1 keV/u) is quite controversial.Considering that the low energy models of heavy ions used in SRIM simply extrapolate the fitting curve of light ions，this would obviously lead to systematical deviation.

Based on numerous experimental results， Sigmund proposed a conjecture named reciprocity theory， in which he believed that when the ion’s velocity is sufficient low，i.e.，slower than Bohr’s velocity(about 25 keV/u)，the ion and target atoms are interchangeable with the stopping power value unchanged:Se(AinB)=Se(BinA).[38]However，this conjecture has not been fully supported by existing models. In order to give a quantitative analysis of the reciprocity theory，the average relative coherent coefficient(¯σrec)was defined as follows:

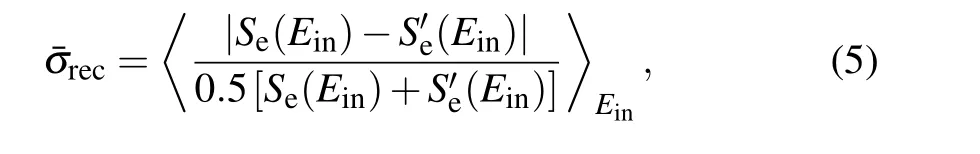
whereSe(Ein)is defined as the electronic stopping power ofAion incident intoBmaterial，whileS′e(Ein)represents the electronic stopping power ofBion intoAmaterial. BothAandBions have the same kinetic energyEin(in units of keV/u);and ¯σrecrepresents the average of absolute relative difference betweenSe(Ein)andS′e(Ein)in a certain energy range for differentEin. The ¯σrec’s forZ1andZ2from 1 to 80 at differentEinwithin the energy range of 1–100 keV/u were calculated using the DL-ESP，SRIM and LSS models，as shown in Fig.4.

As illustrated in Fig.4，we can roughly estimate the general consistency of reciprocity conjecture: the blue zone represents the high consistencyZ1–Z2pair，whose ¯σrecis smaller than 20%， and green zone represents medium consistency，with ¯σrecin the range of 50%–100%. Noticeably， in the red zone，the ¯σrecis over 100%，which means that the reciprocity theory can hardly be tenable under this condition. It can be shown in Figs. 4(a1)–4(a4) that most of the ¯σreccalculated by SRIM are green， especially for the energy range of 5–25 keV/u， which means that SRIM can hardly meet the requirement of reciprocity theory even whenEinsmaller than Bohr’s velocity. In addition，according to Eq.(1)，the ¯σreccalculated by the LSS model would not change with ion’s energy，which leads to the constant ¯σrecin Figs. 4(c)， which means these two models cannot give a reliable support for the reciprocity conjecture.

Fig. 3. According to SRIM’s calculation， there is an obvious difference between Se (Au in Al)and Se (Al in Au)in the low energy range.For DL-ESP， the predicted Se curves are basically coincident， and the Se values in the low energy range are significantly lower than SRIM’s results.

Fig.4. The average relative coherent coefficient(¯σrec)calculated using the DL-ESP(a1)–(a4)，SRIM(b1)–(b4)，and LSS(c)models.

Fig.5. The percentage of average relative coherent coefficient(¯σrec)calculated by(a)the DL-ESP model and(b)the SRIM model，compared to the LSS model(horizontal dashed line in each sub-figure)for different energy ranges.

For DL-ESP，though there are some red zone whenZ1orZ2close to 1， most of theZ1–Z2pairs are in the blue zone，which means that this model can be highly consistent with the conjecture of Sigmund， with the ¯σrecsmaller than 20%. As this model was built based on the combination of experimental data and the LSS model， it could have the advantages of both side at the same time: the behavior ofSefor ion between 5–25 keV/u is much more reasonable than SRIM，and in good consistence with the reciprocity theory. With the help of the DL-ESP model， this conjecture can hopefully be clarified， as shown in Fig.6.

According to Fig.5 that whenEinis under 25 keV/u，over 80% ¯σrecis smaller than 20%， which means thatSe(AinB)are highly consistent withSe(BinA) in this energy range.Moreover， the DL-ESP model also has the highest percent of¯σrec＜20%and ¯σrec＜50%among these models，so it is more in line with the theoretical expectation of reciprocity conjecture than SRIM and LSS.However，it should be noted that the reciprocity theory is just a conjecture based on existing experimental results，which is nearly impossible to be conclusively confirmed by experiments， due to the restriction of measurement technique. This theory is still generally applicable for many potential applications，and the DL-ESP can be hopefully used as a support to promote the validation of this conjecture.

3.4. Applications to ion range prediction

Furthermore，DL-ESP can be applied to give a quick and accurate prediction on the projected range (Rp) of ion in material， which is of great importance for many potential applications， such as doping technique in chip manufacturing.As shown in Fig. 6， we calculated theRpusing DL-ESP and SRIM separately， and compared them with the experimental results. The calculation of ion range using the DL-ESP model is mainly based on Bragg’s theory[50](to convertSeof elementary materials into compounds)and the Lindhard formula，[49]as shown in Eqs.(2)–(4).

As for the ion range calculation， the predictedRpfrom DL-ESP and SRIM are all very close to the experimental result whenEinis small enough(so that the nuclear stopping power dominates)，with the relative difference smaller than 25%，according to Fig. 6. However， whenEinbecomes greater，Rpfrom SRIM calculation becomes less accurate，while the DLESP’s results could still agree well with the experimental data:theRpof 700–5000 keV Au in SiC predicted by SRIM is about 20%–40% lower than experimental results，[53]mainly due to the incorrectly estimated electronic stopping power. Similar deviation is also widely observed in other ion-target combinations such as Cs in SiO2，[54]as shown in Fig. 6(b). As for DL-ESP， the relative difference could be close to 0.6%when 10000 keV Au ion in SiC，and smaller than 1.0%when 300 keV Cs ion in SiO2，which are much better than other classical models. Though Lindhard’s equation has less computational accuracy than Monte-Carlo-based ion range calculation methods(e.g.，the full cascade model in SRIM)，it is still convenient and good enough on many occasions. With the help of deep learning algorithm，the computational accuracy of Lindhard’s equation can be significantly enhanced， which means that a simple way can be provided to quickly estimate the ion range in homogeneous materials，instead of doing full cascade Monte Carlo simulations.

Fig. 6. The projected range (Rp) of Au in SiC predicted by SRIM and DL-ESP.It should be noted that DL-ESP cannot obtain Rp directly.These results are calculated with the help of Lindhard and Bragg’s theory.

4. Conclusion

In conclusion，we have developed a new electronic stopping power model based on the deep learning algorithm to describe the ion-material interaction process.Compared with the classical models，deep learning can extensively avoid the systematic error generated by the fitting model，capture more detailed information of experimental data，and completely eradicate the interference of subjective factors. All these features make DL-ESP exhibit high accuracy for both the conditions with and without experimental data. This model can not only increase the predictive accuracy of ion projected range，but also provide a new insight to challenge the classical puzzles， such as the reciprocity theory， which has been argued for decades. These findings should be of great importance to fundamentally understanding the novel physical phenomena related to the ion interaction with materials， and they are extensively useful for a vast of application areas， such as semiconductor manufacturing and nano-structures fabrication.

Appendix A:Data availability

In order to use DL-ESP to calculate electronic stopping power for a certain incident-target-energy combination， we generated a database for different ions with different energies in different materials. As shown in the supplementary material:there are 81 CSV files，each file represents one kind of incident ion，and the filenameZ1–M1.csv means:Z1andM1are the atomic number and mass of incident ion. In each CSV file，each column represents (from left to right):Z2(atomic number of target element)，M2(atomic mass of target element)，Ein(kinetic energy of incident ion， in units of keV/u)，Se(electronic stopping power，in units of 1×1015eV·cm2/atom). The training data used in this article are also attached in the supplementary material.

Acknowledgements

We are grateful for computing resource provided by Weiming No. 1 and Life Science No. 1 High Performance Computing Platform at Peking University， and TianHe-1(A)at National Supercomputer Center in Tianjin.

Project supported by the National Natural Science Foundation of China (Grant Nos. 12135002 and 11705010)，the China Postdoctoral Science Foundation(Grant No.2019M650351)，and the Science Challenge Project(Grant No.TZ2018004).