Solutions of novel soliton molecules and their interactions of(2+1)-dimensional potential Boiti–Leon–Manna–Pempinelli equation

Hong-Cai Ma(马红彩)， Yi-Dan Gao(高一丹)， and Ai-Ping Deng(邓爱平)

Department of Applied Mathematics，Donghua University，Shanghai 201620，China

Keywords: variable separation method，Hirota bilinear method，dromion solution，(2+1)-dimensional poten

1. Introduction

The exploration of the linear field is not enough to describe the complex natural phenomena， so the exploration of the nonlinear field is born at the right time， and the study of nonlinear system has become one of the important tasks in the field of nonlinear science. Nonlinear equations are widely used in mathematics， physics， biology， astronomy， communication， and many other fields， it is of great significance to solve nonlinear equations. The variables separation method has undoubtedly become one of the powerful tools for obtaining exact solutions of nonlinear equations. In recent years，scholars have spared no effort to perfect this method， and they have proposed many methods. For example， nonlinearization method[1](formal separation of variables[2])， multiple linear variable separation method，[3]function variable separation method，[4]derivative dependent variable separation method，[5，6]and so on.Up to now，after the unremitting efforts of scholars， the separation of variables has been successfully used to nonlinear equations.[7–16]

By solving the exact solutions of nonlinear system，many interesting local excitation modes have been found.[17–19]This diversity of exact solutions is also shown in the Hirota bilinear method.[20]In addition， Maet al.proposed a generalized algorithm to test Hirota’s condition and to prove the existence ofN-soliton solutions for nonlinear equations in Refs. [21–23]. This method has been applied to nonlocally integrable equations.[24]

Recently， the soliton molecules obtained by using the mechanism of velocity resonance has aroused a great deal of interest. The velocity resonance mechanism was first proposed by Lou in Ref.[25]，and a variety of soliton molecules were obtained by using this method.[26，27]Using velocity resonance mechanism， module resonance， and long wave limit method， researchers obtained new hybrid solutions between soliton molecules， lump waves， and breather waves， and explored their interactions.[28–36]In this article， we will apply the variable separation method to get the dromion molecules，ring molecules， lump molecules， and multi-instantaneous molecules of the (2+1)-dimensional potential Boiti–Leon-Manna–Pempinelli(pBLMP)equation， and we will show the interesting interactions between these molecules. The(2+1)-dimensional pBLMP equation[37]is

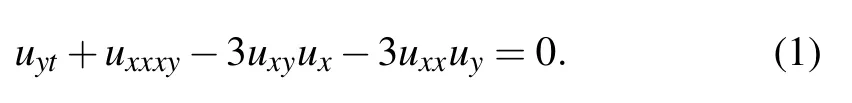
Many studies have been done for Eq.(1)by predecessors.Seadawyet al.used an improved extended assisted mapping method to obtain several exact and isolated wave solutions of Eq.(1).[38，39]Kaplan constructed the analytic solution by using transformation rational function method and exp(Φ(ξ))method in Ref.[40].Heet al.studied the“new”interaction solutions between block solutions and other multi-soliton(kink or banding) solutions by developing a “new” direct method based on Hirota’s bilinear form for(2+1)-dimensional BLMP equation.[41，42]Kumaret al.solved the exact solution by the theory of Lie group transformation and studied its physical properties in Ref.[43]. Huet al.obtained Pfaffian solution by using Pfaffian technique and real auxiliary functionφ(y).[44]Shenet al.derived the periodic wave solution by using Riemann function and constructed the respiratory wave solution by using the extended homoclinic test method.[45]

By giving the hypothesis，we can get the solutions by separating the variables of Eq.(1). Based on multi-linear variable separation method，we can further obtain many local excitation modes of Eq.(1).In Section 2，we use the multi-linear variable method to solve Eq.(1)，and under this assumption，we take it a step further to analyze the general quantities valid for a large number of separable systems with multi-linear variables. In Section 3， we draw three cases of dromion solution and explore the corresponding motion rules. The motion of dromion molecules at common velocity is also given. In Section 4，we draw ring molecule with symmetry and give two cases of ring solutions. In Section 5，we plot three cases of lump molecules that can formN×Mlattices and multi-instanton molecules with energy decaying but the shape unchanged. Finally we make some summaries and put forward some ideas.

2. Multilinear variable separation approach

Supposing the form of solution is[46]

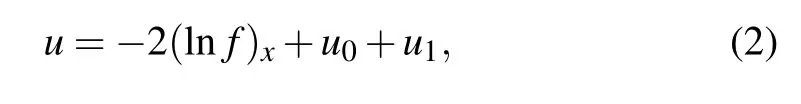
whereu0=u0(x，y)，u1=u1(t) are seed solutions， by substituting Eq. (2) into Eq. (1) and integrating aboutxonce， we obtain

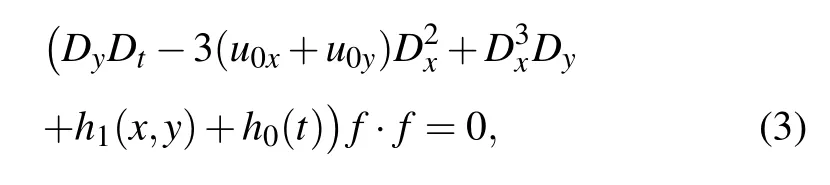
whereh1is a function ofxandy，h0is a function oft，and the Hirota’s bilinear operator is defined by

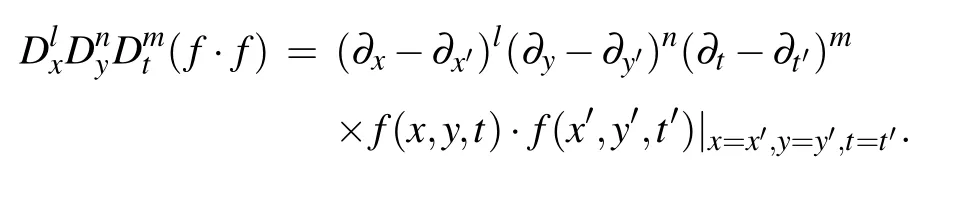
Supposingfhas the following form

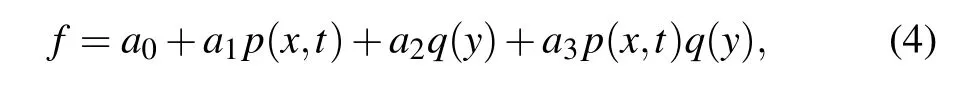
taking Eq.(4)into Eq.(3)，then we acquire

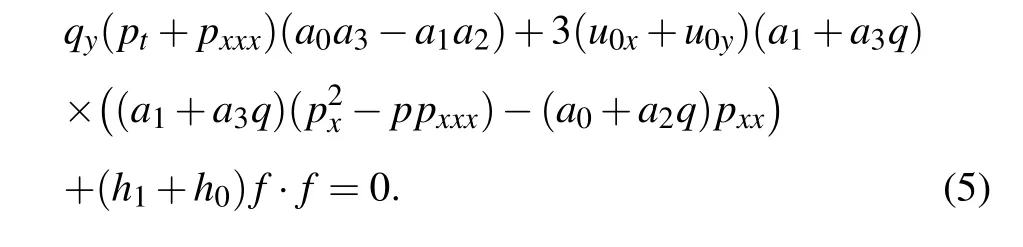
Obviously，when

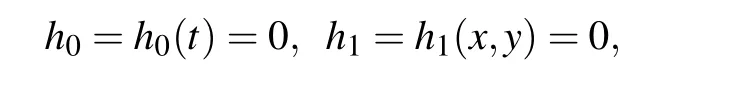
equation(1)can be solved by variabls separation. Therefore，we consider Eq.(1)as one of the multilinear variable separation approach (MLVSA) solvable models， and there are a lot of local excitation patterns. In the case of Eq.(4)，equation(2)becomes

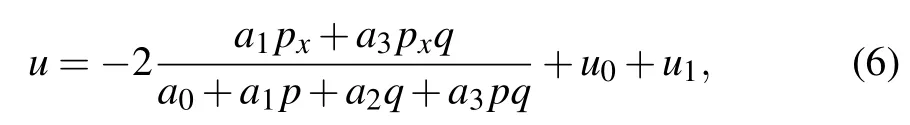
the potential fieldU ≡uyfrom Eq.(6)is written as

whereUis a general quantity valid for a large number of separable systems with multiple linear variables. It is the randomicity of the seed solutionu0that leads to the existence of a large number of different local excitation modes.[17，18，47]In the following sections， we will map four novel soliton molecules and their interactions.

3. Dromions， dromion molecules， and their interactions

In order to gain the dromion molecule of Eq.(1)，we takepandqas follows:

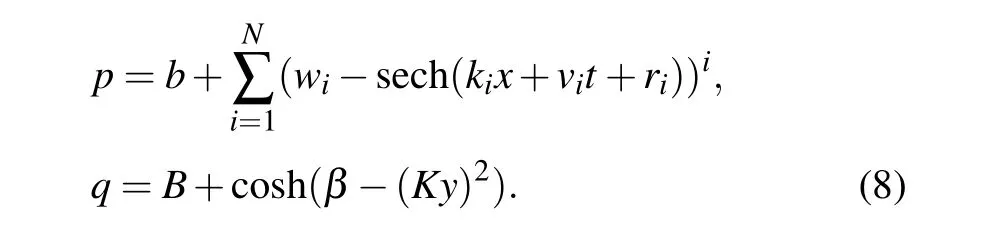
The parameter of Eq.(4)in this part is going to take the value ofa0=2，a1=1，a2=1，a3=1.

Case 1 ForN= 2， by taking the parametersb= 5，w1=3，k1=1，v1=3，r1=5，w2=1.5，k2=1，v2=-2，r2=-5，B= 2，β= 2，K= 1， we observed the collision phenomenon of dromion molecules with time increasing，then they separate， and there is no energy loss in collision processes， so it is considered as an elastic collision as shown in Fig. 1. If the parameters satisfyk1/k2=v1/v2， two dromion“atom” can be considered to have a common velocity and bound to a one dromion molecule by takingk1=3，k2=1，v1=6，v2=2，and other parameters remain unchanged.

As shown in Fig. 2， we observed that the new dromion molecule moves negatively alongxaxis with time increasing，but does not move inyaxis.We also note that the parameterwiis the main factor affecting the shape of dromion molecules.

Case 2 ForN=3，by takingb=3，w1=3，k1=1，v1=3，r1=5，w2=2，k2=1，v2=-3，r2=-5，w3=1，k3=2，v3=-1，r3=3，B=0，β=0，K=1，we plot a 3D diagram for dromion molecule of Eq.(8)as shown in Fig.3，it is obvious that the three dromion molecules move from their original position to opposite direction with the increase of time. Whent=-2，the three dromion molecules collide and fuse together，the collision is also elastic. And then they separate again. We found that the parameterβaffects the internal spacing of each molecule. Whenβ ＞0，the internal spacing of each molecule increases with the increase ofβ. Whenβreaches a certain value，we get six dromions which are situated in two rows and three columns.

Case 3 WhenN=3，we also study two cases of the common velocity. The first kind of circumstance is two molecules keeping pace consistent，by takingk1=1，k3=2，v1=2，andv3=4，other parameters beingb=3，w1=3，r1=8，w2=2，k2= 1，v2=-3，r2= 7，w3= 1，r3= 2，K1= 1，B= 0，β=0. Under these conditions， we draw a 3D plot of threedromion molecules moving with time increasing as shown in Fig. 4， two dromion “atoms” are bound to a single dromion molecule， which moves forward at a common speed and collides with the third “atom” att=-2.7. After this process，they move forward in the original direction. And the velocity does not change. The second case is to make a total of three molecules，namely under the parameters of the first kind of circumstance， changing byk2=1，v2=2， then meetimgki/kj=vi/vj， 1≤i ＜j ≤3， Fig. 5， we observed the three molecules along thexaxis at the same rate to the negative direction.

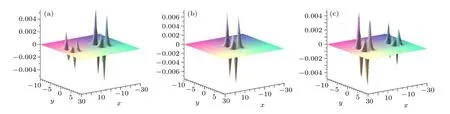
Fig.1. A three-dimensional(3D)plot of the dromion solution of Eq.(8)for N=2: (a)t=-8，(b)t=-2.2，and(c)t=4.

Fig.2. The 3D plot of dromion molecule of Eq.(8)for N=2 when k1/k2=v1/v2: (a)t=-5，(b)t=0，and(c)t=5.

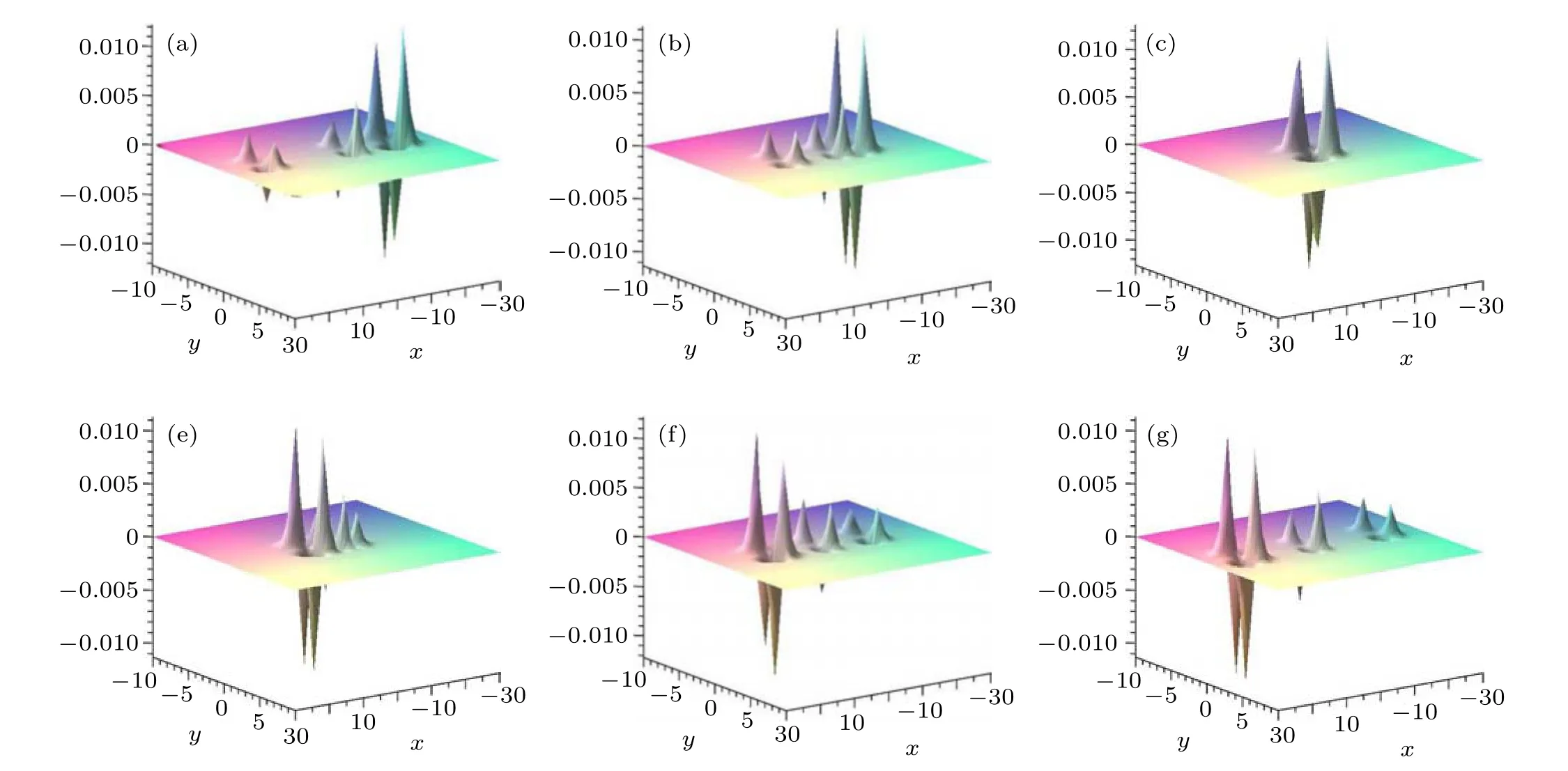
Fig.3. The 3D plot of three dromion molecules moving with time increasing for N=3: (a)t=-8，(b)t=-5，(c)t=-2，(d)t=0，(e)t=3，and(f)t=5.

Fig.4. For N=3，the 3D plot of the elastic collision of dromion molecule and new dromion molecule with time increasing when k1/k3=v1/v3: (a)t=-8，(b)t=-2.7，and(c)t=4.

Fig.5. For N=3，the 3D plot of dromion molecule moving with time increasing when ki/kj =vi/vj: (a)t=-4，(b)t=0，and(c)t=4.

4. Rings，ring molecules，and their interactions

In order to obtain the ring molecule of Eq.(1)，we takepandqas follows:

The parameters of Eq.(4)in this part are taken the values ofa0=2，a1=1，a2=1，a3=0.

Case 1 WhenM=N=1，by taking parametersd=1，w1=10，k1=1，b1=5，v1=-1，D=1，K1=-1，B1=5，θ1=1，equation(9)is the ring soliton solution which is the centrosymmetric graph of the central point at(-5，-5)as shown in in Fig.6.

Case 2 WhenM=2 andN=1，by takingd=1，w1=10，k1=0.8，b1=5，v1=-5，w2=5，k2=0.8，b2=-5，v2=2，D=1，K1=2，B1=5，θ1=1. We construct two ring molecules that are different in size and exactly the same in shape. In Fig.7，we plot the images and their corresponding density images att=0.4，t=1.5，andt=2.5，respectively. Whenv1／=v2／=0，the two molecules move alongxaxis at the speed oftx=(b1v2-b2v1)/(k1v2-k2v1).

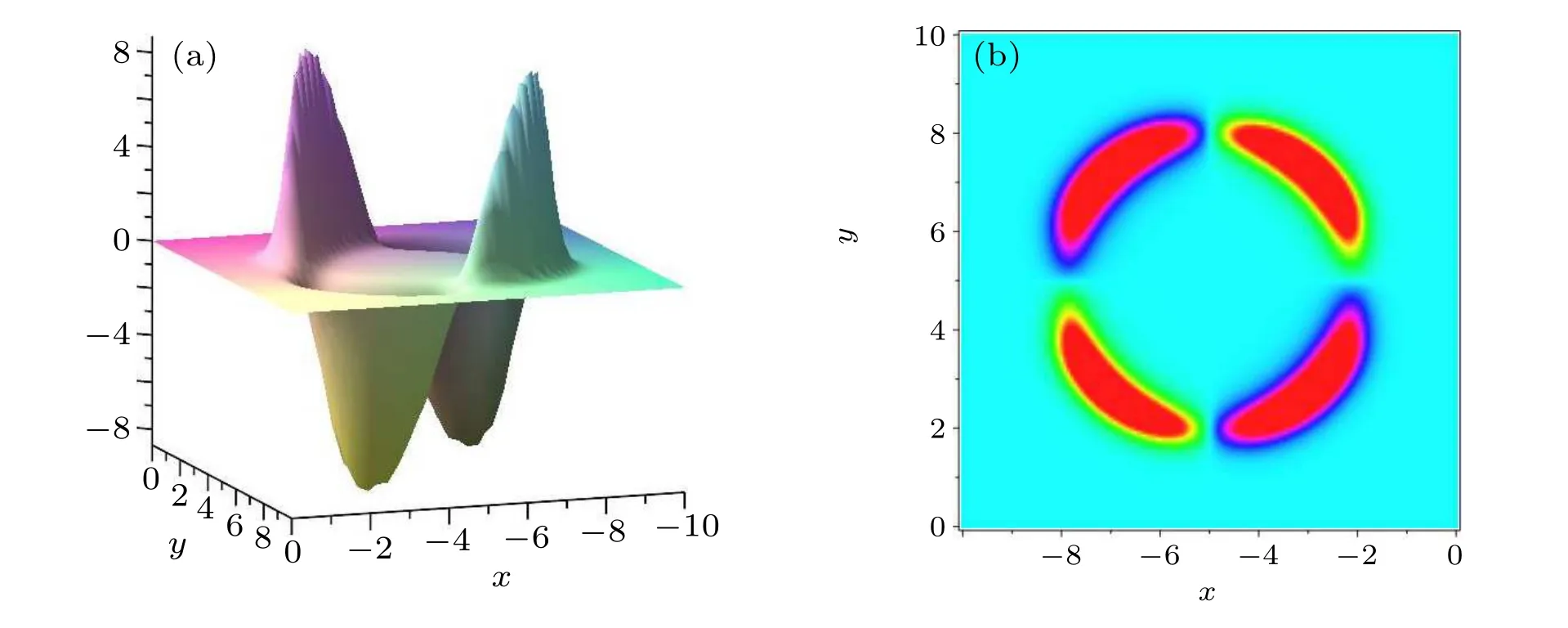
Fig.6. The 3D plot and density plot of Eq.(9)for M=N=1 at t=0.

Fig.7. The 3D plot and density plot of the interaction between two ring molecules when M=2，N=1 for(a)t=0.4，(b)t=1.5，and(c)t=2.5.

5. Other molecules

5.1. Lump molecules

In order to gain the lump molecule of Eq.(1)，we takepandqas follows:The parameters of Eq.(4)in this part are taken the values ofa0=1，a1=1，a2=1，a3=2.

Case 1 WhenM=N=2，the parameters are taken asc=1，v1=1，k1=1，b1=5，v2=3，k2=1，b2=-5，C=5，K1=1，B1=-8，K2=1，B2=8，we draw the 3D image and density diagram att=0 as shown in Fig.8.WhenM=N=2，equation(10)forms the lump molecule constituted of 2×2 lump“atoms”.

Case 2 WhenM=3 andN=1，the parameters arec=1，v1=-3，k1=1，b1=5，v2=1，k2=1，b2=-5，v3=3，k3=1，b3=15，C=-5，K1=1，B1=-2. Under these conditions，we construct the lump molecule for 1×3 lattice. The 3D image and the corresponding density diagram are shown in Fig.9 att=0.

Case 3 WhenM=2 andN=3，the parameters arec=1，v1=1，k1=1，b1=5，v2=3，k2=1，b2=-5，C=5，K1=1，B1=-4，K2=1，B2=4，K3=1，B3=12. Under this condition，we construct lump molecule for 3×2 lattice. The 3D image and the corresponding density diagram are shown in Fig.10 att=0.

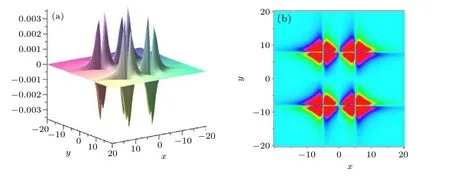
Fig.8. The 3D plot and density plot of Eq.(10)for M=N=2 at t=0.

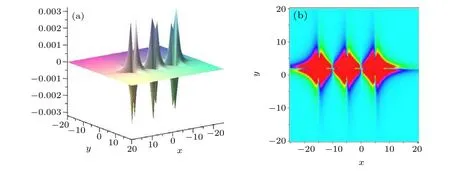
Fig.9. The 3D plot and density plot of Eq.(10)for M=3，N=1 at t=0.

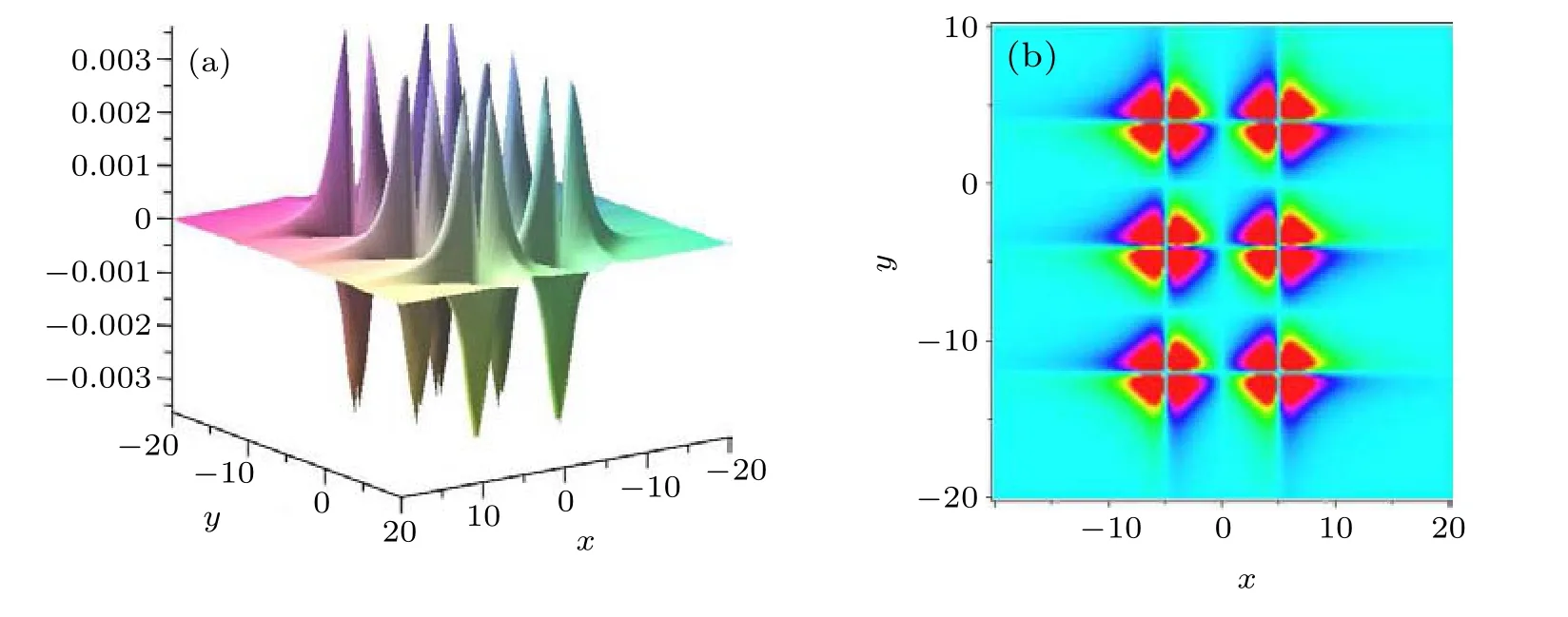
Fig.10. The 3D plot and density plot of Eq.(10)for M=2，N=3 at t=0.

Through the analysis of the above three cases，it is concluded that the lump solutions constructed by Eq.(10)can form lump molecules withNrows andMcolumns by choosing appropriate parameters，i.e.，the formation ofN×Mlattice.

5.2. Multi-instantaneous molecule

In order to gain the multi-instantaneous molecule of Eq.(1)，we takepandqas follows:

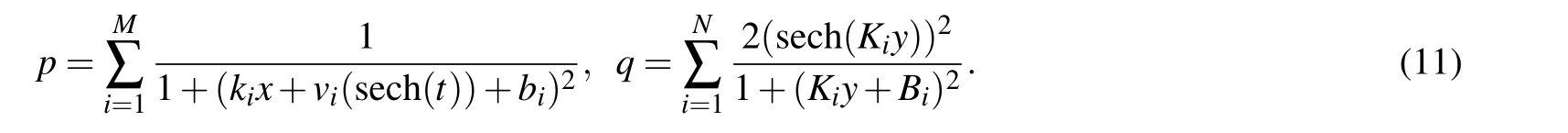
The parameters of Eq.(4)in this part are taken the values ofa0=1，a1=1，a2=1，a3=2.

WhenM=N=2， by choosinga0=1，a1=1，a2=1，a3=2，k1=1，v1=1，b1=5，K1=1，B1=-8，k2=1，v2=3，b2=-5，K2=1， andB2=8， we draw a 3D image of Eq. (11) and its density diagram att=5 in Figs. 11(a) and 11(b). By observing the image，we find the graph of density plot is centrosymmetric and(0，0)is the symmetric point. The image shape and position of the multi-instantaneous molecule does not change with time，but its energy decays with time until it decays to 0. In order to more intuitively observe the changing trend of the energy，we plot the energy curve att=0，t=1，t=2 in Fig.11.

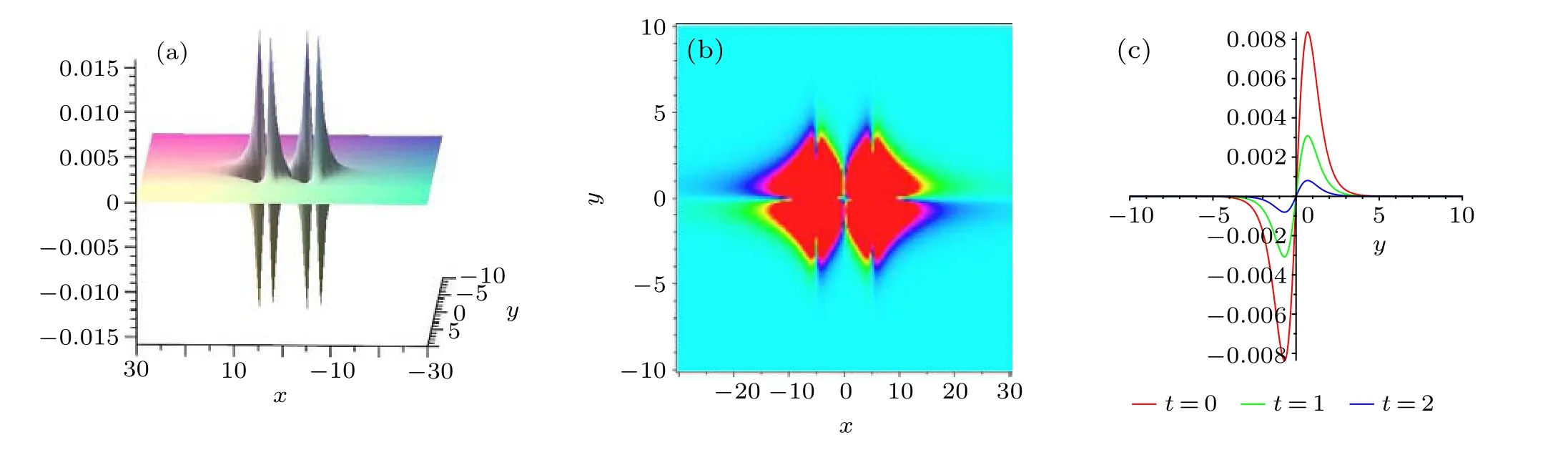
Fig.11. (a)and(b)The 3D plot and density plot of Eq.(11)for M=N=2 at t=5，(c)the energy curve of Eq.(11)at t=0，t=1，t=2.

6. Conclusion

In this paper，we first use the variable separation method to solve the(2+1)-dimensional potential BLMP equation. By taking appropriate assumptions，we conclude that equation(1)can be separated by variables under the given conditions. And the solutions under these conditions satisfy the general formulaUapplicable to most systems in which variable separation can be carried out. Then we know that Eq. (1) has a large number of local excitation modes in the form of Eq.(7).Therefore， we give four intuitive excitation modes， and draw the corresponding soliton molecules.

We plot dromion molecules whenN= 2 andN= 3，and add the covelocity conditions while studying the motion， so that we could study the motion behavior when two or three dromion“atoms”are bound into a dromion molecule.Through the above studies，we come to the conclusion that no matter how to change their motion forms，the interactions between molecules are always elastic and they move along thexaxis without changing their motion direction and speed. Then we plot the ring molecules and find that the interactions between the molecules are still elastic. We also plot two very interesting types of excitation patterns. Under the condition of Eq. (10) ， the 3D plot of the lump molecule ofN×Mlattice will always be formed by taking appropriate parameters. In addition，we also draw a multi-instantaneous molecule whose shape does not change with time，but the energy decays to zero with time.

In this article，we adopted a relatively simple assumption for the(2+1)-dimensional potential BLMP equation and carried out variable separations.In fact，there could be some other forms of solutions that could be used to separate variables.Besides the four moleculars mentioned in this paper， there are still a lot of interesting excitation modes waiting for readers to explore. We hope that our results can further explain and enrich the dynamic behavior of nonlinear evolution equations，and also hope that our research can make some contributions to the research of mathematics and physics.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos. 11371086， 11671258， and 11975145)and the Fund of Science and Technology Commission of Shanghai Municipality(Grant No.13ZR1400100).