基于DIN 743标准的电机转轴强度校核方法及其验证

张 焱

(上海电气集团上海电机厂有限公司，上海 200240)

0 引言

转轴在电机中起到支撑转子、传递扭矩的作用，是电机最关键的部件之一，因此，保证转轴强度满足要求对电机的安全性具有重要意义。目前国内常用的电机转轴强度校核方法种类较多，不同厂家均有各自的计算方法，同时，有限元分析技术也逐步得到应用。德国DIN机械工程标准委员会编写的《DIN 743轴类部件的承载力计算》标准涵盖了多种转轴几何结构特征的强度校核方法，计算较为准确，具有较高的应用价值。

1 DIN 743标准中的转轴校核方法

DIN 743标准主要通过计算安全系数对转轴的疲劳失效和永久变形进行校核，将计算得到的安全系数与固定值Smin=1.2进行比较，以判断轴是否处于安全状态。

1．1 防止疲劳失效的证明

疲劳安全系数的计算公式如下：

式中：σzda、σba、τta外力作用下产生的主动应力幅值，其作用形式为拉伸/压缩、弯曲和扭转，σzdADK、σbADK、τtADK为可承受幅值(拉伸/压缩、弯曲和扭转的强度)。

部件的疲劳强度σzd，bADK，(τtADK)通过抛光试棒的强度加以计算得出。作为名义应力，表示该部件在所述负载情况下的最大可承受振幅。应考虑以下因素：

(1) 热处理质量和淬火性：若无法通过相关截面的硬度测量等方式直接获得，可近似取决于部件的直径(工艺尺寸影响因子K1(deff))。

(2) 随着应力梯度的减小，弯曲振动强度随直径的增大向拉伸/压缩振动强度转变(几何尺寸影响因素K2(d))。

(3) 部件形状，尤其是缺口形状(疲劳缺口因子βσ(d)、βτ(d))。

(4) 表面粗糙度(粗糙度因子KFσ和KFτ)。

(5) 表面硬化和作用于表面的残余应力的影响(表面调整因子KV)。

(6) 平均应力对可承受应力幅值的影响(平均应力敏感度因子ΨσK和ΨτK)。

拉伸/压缩和弯曲的总影响因子Kσ

扭转总影响因子Kτ

其中βσ，τ定义为

式中：σzd，bWK、τtWK是在切口横截面处具有直径d的部件在反向应力下的疲劳极限(以公称应力表示)，σzd，bW(d)、τtW(d)是在另外相同条件下，直径为d的无缺口抛光圆形试验棒在反向应力下的疲劳极限。可通过实验计算或测定拉伸/压缩，弯曲βσ或扭转βτ的疲劳缺口系数，视具体情况而定。

1．2 防止永久变形的证明

屈服安全系数的计算公式如下：

式中：σzdmax、σbmax、τtmax为工作负荷引起的现有最大名义应力，使用最大发生负荷Fzdmax’、Mbmax、Mtmax来确定，σzdFK、σbFK、τtFK为部件拉伸/压缩、弯曲和扭转的屈服点。

部件的屈服点是计算防止永久变形安全系数的依据。以相关部件横截面的屈服强度σS(d)为起点，如果该信息未知，σS(d)可通过试棒直径dB(参考直径)的有效屈服强度和尺寸因子K1(deff)(即σS(d)=σS(dB)·K1(deff))取近似值确定。使用此方法时，部件的屈服点应使用下式计算

σzd，bFK=K1(deff)·K2F·γF·σS(dB)

式中：K1(deff)为工艺尺寸影响因子(热处理质量、淬火性)，见DIN 743-2关于屈服强度的描述；K2F为表面局部塑性变形后的静态支持因子。对硬表面，K2F=1(表面以下值的计算)；γF为圆周缺口处多轴应力条件和局部硬度增加而导致屈服点增加的因子。对于硬表面或无圆周缺口的情况，γF=1；σS(dB)为参考直径dB的屈服强度，见DIN 743-3；对于硬表面的情况，应使用核心的值。

2 与其他校核方法的对比

2．1 电指(DZ)21-63大型电机机械计算公式

利用《电指(DZ)21-63大型电机机械计算公式》校核转轴强度时，首先根据工况确定疲劳计算过载系数Kp，然后考虑转轴材料、结构、尺寸等因素，计算得到应力集中系数，从而进一步计算安全系数，相应参数曲线见图1。

图1 《电指(DZ)21-63大型电机机械计算公式》中相应曲线

式中：σ-1为材料的耐久限值；Kσ为应力集中系数；σx,d为按疲劳计算的相当应力。安全系数建议选用1.6～1.7。

2．2 《机械设计手册》

《机械设计手册》中校核方法形式与DIN 743较为接近，在具体公式和参数计算上有所区别，同样考虑应力集中、表面质量、尺寸、平均应力折算系数等影响因素。危险截面安全系数S的校核计算公式为

式中：Sσ为只考虑弯矩作用时的安全系数；Sτ为只考虑转矩作用时的安全系数。

2．3 DIN 743标准与上述校核方法对比

各校核方法对比情况见表1，可以看出，相较于其他标准，DIN 743对转轴结构覆盖更加全面，各参数均通过公式计算得到，准确性好，同时在国际上也有较高的接受度。因此，使用DIN 743标准进行转轴强度校核是较为合适的。

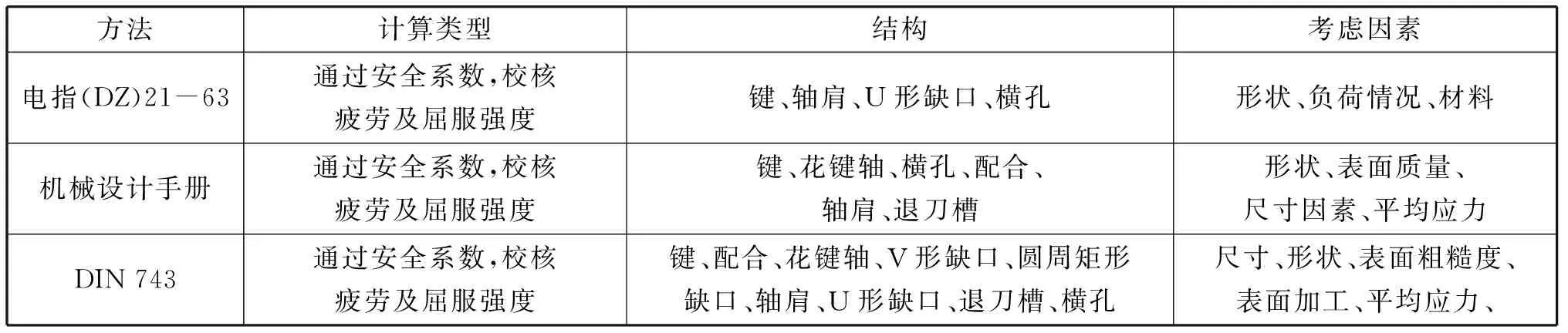
表1 各校核方法对比

3 校核方法的有限元验证

在依据DIN 743标准的工程计算中，可以根据截面几何参数，计算得到结构特征处应力集中系数α，其含义为此处最大应力与名义应力的比值：

式中：σmaxK是由于线性弹性材料性能的缺口效应导致的计算截面上表面的最大主应力；τtmaxK为最大局部扭转应力；σn，τtn为名义应力，通常是指根据基本强度理论(DIN 743-1)计算，在最小缺口横截面处的应力，不考虑具有线弹性材料性能的缺口效应。

因此，可以通过有限元仿真得到危险截面处缺口最大应力和名义应力，与工程计算结果相对比，验证计算的准确性。

3．1 验证案例1

针对某电机转轴轴伸端危险截面进行强度校核与对比分析，截面参数见表2：

表2 验证案例1截面几何参数

根据DIN 743标准计算得，截面1扭转应力集中系数ατ=1.7 587。

与图2有限元结果进行对比：

图2 验证案例1有限元结果

名义应力τn=202.95 MPa

最大应力τmax=375.13 MPa

DIN 743结果ατ×τn=356.93 MPa

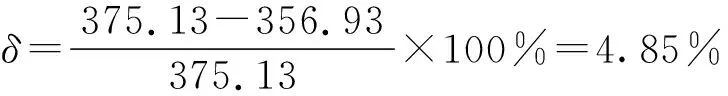
可以认为DIN 743计算结果与有限元计算结果相符。

3．2 验证案例2

针对某电机转轴轴伸端危险截面进行强度校核与对比分析，截面参数见表3：

表3 验证案例2截面几何参数

根据DIN 743标准计算得，截面1扭转应力集中系数ατ=1.8 274。

与图3有限元结果进行对比：

图3 验证案例2有限元结果

名义应力τn=142.17 MPa

最大应力τmax=268.54 MPa

DIN 743结果ατ×τn=259.80 MPa

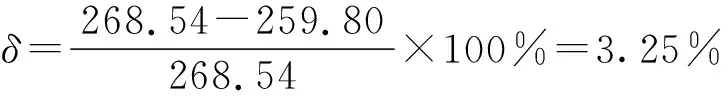
可以认为DIN 743计算结果与有限元计算结果相符。

3．3 验证案例3

针对某电机转轴轴伸端Ⅰ、Ⅱ两危险截面进行强度校核与对比分析，截面参数见表4、表5：

表4 验证案例3截面Ⅰ几何参数

表5 验证案例3截面Ⅱ几何及材料参数

3．3．1 截面Ⅰ

根据DIN 743标准计算得，截面Ⅰ扭转应力集中系数ατ=1.6 889。

与图4有限元结果进行对比：

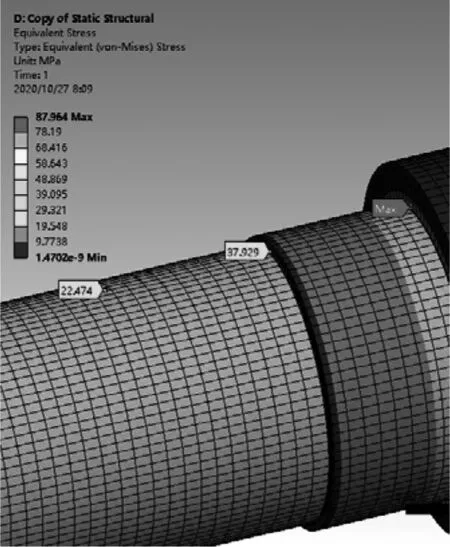
图4 验证案例3截面Ⅰ有限元结果

名义应力τn=22.474 MPa

最大应力τmax=37.929 MPa

DIN 743结果ατ×τn=37.956 MPa

可以认为工程计算结果与有限元计算结果相符。

3．3．2 截面Ⅱ

根据DIN 743标准计算得，截面Ⅱ扭转应力集中系数ατ=3.6 522。

与图5有限元结果进行对比：

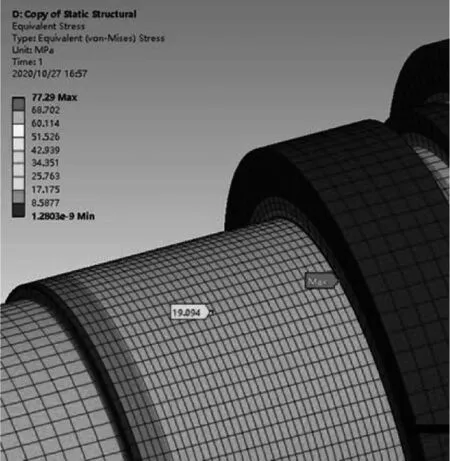
图5 验证案例3截面Ⅱ有限元结果

名义应力τn=19.094 MPa

最大应力τmax=77.29 MPa

DIN 743结果ατ×τn=69.735 MPa

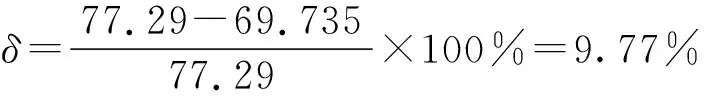
此案例误差较大，但仍在10%以内。

3．4 验证案例4

针对某电机转轴轴伸端Ⅰ、Ⅱ两危险截面进行强度校核与对比分析。

3．4．1 截面Ⅰ

根据DIN 743标准计算得，截面Ⅰ扭转应力集中系数ατ=1.7 396。

与图6有限元结果进行对比：

图6 验证案例4截面Ⅰ有限元结果

名义应力τn=35.626 MPa

最大应力τmax=64.432 MPa

DIN 743结果ατ×τn=61.975 MPa

可以认为工程计算结果与有限元计算结果相符。

3．4．2 截面Ⅱ

根据DIN 743标准计算得，截面Ⅱ扭转应力集中系数ατ=1.6 601。

与图7有限元结果进行对比：

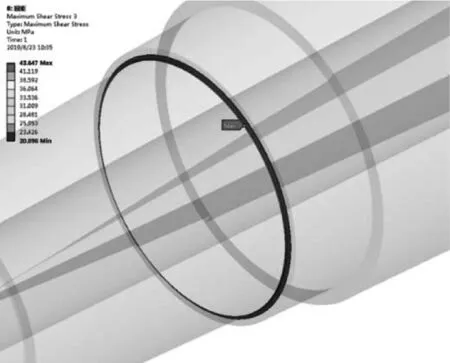
图7 验证案例4截面Ⅱ有限元结果

名义应力τn=25.015 MPa

最大应力τmax=43.467 MPa

DIN 743结果ατ×τn=41.527 MPa

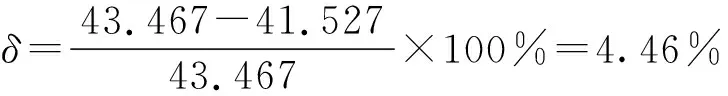
可以认为工程计算结果与有限元计算结果相符。

4 结论

本文对德国DIN 743标准中的转轴强度校核方法进行了介绍，并与其他几种转轴强度校核方法进行了对比，利用有限元仿真对方法的准确性进行了验证。结果表明，建立的电机转轴强度工程计算校核方法具有较高的准确性与适用性，可以用于电机转轴强度校核。