横观各向同性岩体平直-光滑节理双模型细观参数联合标定方法

王朝阳，林鹏，许振浩，王文扬，吴杰

(1.山东大学岩土与结构工程研究中心，山东济南，250061；2.山东大学土建与水利学院，山东济南，250061；3.山东大学齐鲁交通学院，山东济南，250061)

自然界中含定向组构单元的岩石(体)通常被作为横观各向同性岩石(体)进行研究[1]。颗粒流程序(PFC)将介质材料离散为刚性颗粒的集合，颗粒之间通过黏结键进行连接，使其在力的作用下可以发生分离，具备模拟岩土体大变形的能力[2-3]。但PFC颗粒之间采用接触本构模型，导致细观参数与真实材料的宏观参数不直接对应，为获得理想的宏观参数必须标定模型输入的细观参数[4-5]。

横观各向同性岩体采用PFC 进行模拟时通常被看作含平行节理的岩体，建模时采用生成岩石后再嵌入节理的方法[6-7]。传统嵌入节理采用降低节理区域黏结强度或去除黏结实现[8-10]，但是在节理滑动过程中颗粒相互阻挡，存在微观尺度的粗糙问题；光滑节理模型(SJM)设置平行于节理的平面，允许颗粒相互重叠或通过，从而解决了该问题[11]。目前，横观各向同性岩体建模大量采用光滑节理模型(SJM)[12-15]。在光滑节理模型引入后，岩石和节理采用不同模型建模，双模型建模的横观各向同性岩体虽然更接近于真实岩体，但对于细观参数标定存在2个问题：

1)双模型细观参数数量众多，导致宏观-细观参数对应关系复杂，从而造成标定困难。在PFC的接触本构模型中，平行黏结模型(LPBM)和平直节理模型(FJM)更适用于岩石材料的模拟，对于横观各向同性岩体多采用平行黏结模型(LPBM)对岩石部分进行建模[16-17]。众多学者发现平行黏结模型存在压拉比过高的问题，而平直节理模型能较好地解决这一问题[18-21]。但采用平直节理模型(FJM)和光滑节理模型(SJM)对横观各向同性岩体进行建模，需要标定的细观参数数量增加，带来了更复杂的宏观-细观参数关系，导致标定困难。

2)模型内和模型间细观参数共同影响同一宏观参数，即细观参数非独立，导致细观参数相互干扰，造成标定困难。宏观参数被多个细观参数显著影响，而每个细观参数又会影响多个宏观参数，在标定过程中，当一个细观参数改变，为保证宏观参数不变，其余细观参数必须做出调整，而调整后又会影响其他宏观参数，引发整个参数体系的改变，进而导致标定失败。较多学者对采用双模型建模的横观各向同性岩体的标定方法进行了研究[1,5,22-23]。目前，采用双模型对横观各向同性岩体进行标定，需要将不同模型参数先后标定，但是不同模型参数之间存在相互影响，所以在标定过程中需要充分考虑双模型之间的联系。

针对上述问题，本文提出了基于平直节理模型(FJM)和光滑节理模型(SJM)的横观各向同性岩体细观参数联合标定方法(CM-FJM&SJM)。该方法采用参数标定指标体系，分析细观参数的敏感性，得到了细观参数对宏观参数的影响关系，建立了FJM 和SJM 全参数标定优先级，构建了宏细观参数函数表征体系，并采用迭代校准方法来提高参数标定的准确性，最后给出了一套针对横观各向同性岩体的标准化细观参数标定流程。

1 标定参数指标体系

通过改变连接的性质，颗粒流程序中细观参数直接影响数值模型的宏观响应与宏观参数，为确定核心细观参数指标，需要对细观参数进行筛选与简化。

1.1 细观参数

本文采用FJM 和SJM 对横观各向同性岩体进行建模，探究细观参数标定方法。横观各向同性岩体采用平直节理模型生成岩石部分，平直节理模型需要输入的细观参数如表1所示，CUNDALL等[24]研究表明，当交界面段数N为4个，平直节理半径乘数λ*为1，平直节理内摩擦角φ*为0 时，数值模拟实验结果与岩石材料性能较一致。因此，细观参数强度比主要影响岩石压拉强度比，陈鹏宇等[25]在模拟灰岩力学行为时将细观参数强度比设置为9.4，得到压拉强度比为22.74。

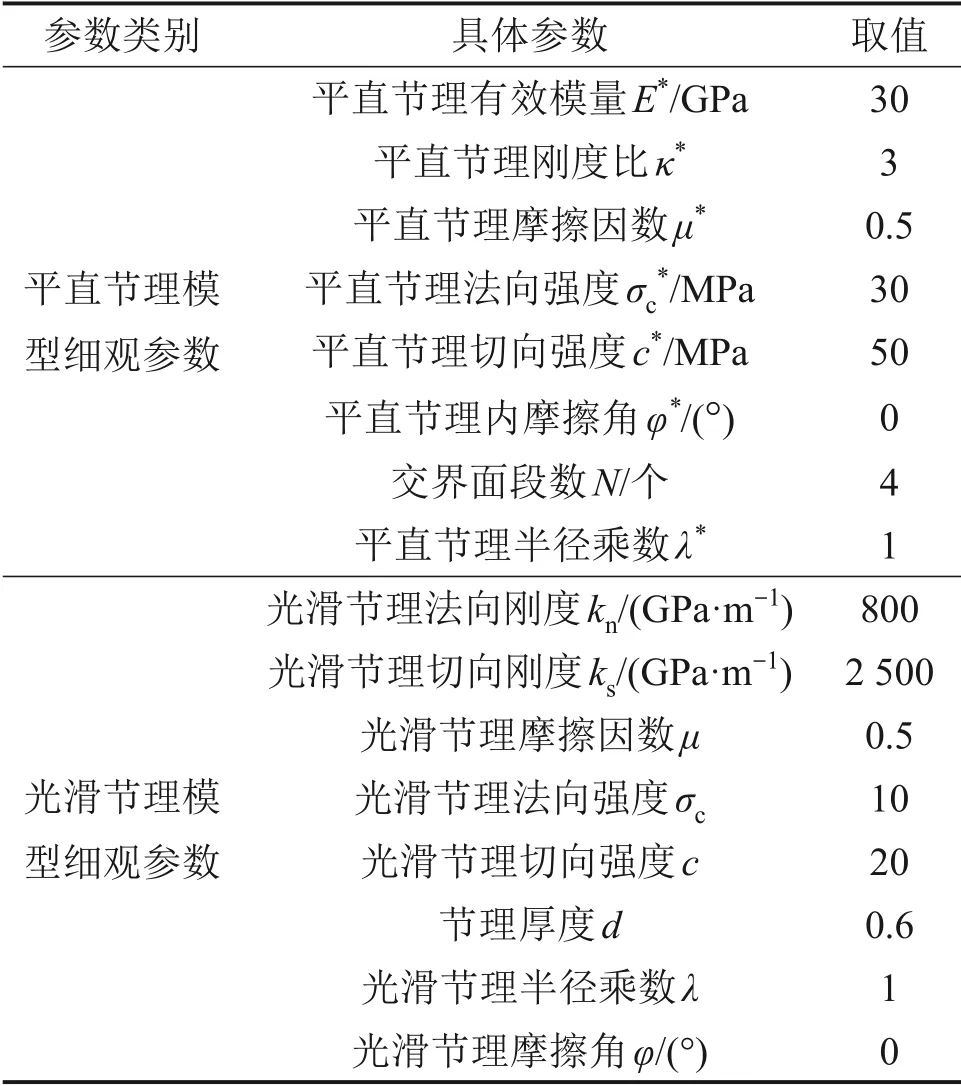
表1 横观各向同性岩体标定参数指标体系Table 1 Transversely isotropic rocks calibration parameter index system

生成节理部分的SJM 需要输入的细观参数如表1所示。YIN 等[5,22]模拟横观各向同性岩体时对半径乘数λ取1，对光滑节理摩擦角φ取0，取得了较好的模拟效果。节理走向设置为0°，节理倾角分别设置为0°，15°，30°，45°，60°，75°和90°。

1.2 宏观参数

开展数值单轴压缩试验，需要获取的宏观参数包括含不同节理倾角岩体的单轴抗压强度σθ、弹性模量Eθ、节理宏观法向刚度Kn、宏观切向刚度Ks。其中σθ和Eθ可以直接从应力-应变曲线获得。GOODMAN[26]提出，对于节理宏观刚度的获取，如果岩石被单一节理有规律切割，就有可能计算出与岩体等效的连续材料表征的弹性常数。假设岩石为各向同性，符合线弹性本构理论，节理面规则排列，横观各向同性岩体弹性模量的解析解可由式(1)获取：

式中：E为完整岩石弹性模量；θ为节理倾角；δ为节理间距。

对含不同节理倾角的岩体进行数值压缩试验，获取应力-应变曲线，提取σθ与Eθ信息。将Eθ代入式(1)，采用最小二乘法得到节理面的宏观刚度Kn和Ks。值得注意的是，式(1)使用条件为节理部分不承受走向的压力，但数值模型节理部分具有真实厚度且承担沿走向的压力，在倾角由0°增大的过程中，对于沿走向的压力承担逐渐增大。因为节理部分的弹性模量一般比岩石部分的小，导致Eθ一般偏小。

综合上述，本文作者提出横观各向同性岩体标定参数指标体系，见表1。

2 横观各向同性岩体建模与细观参数敏感性

横观各向同性岩体采用PFC3D进行建模，完整岩石部分颗粒间接触采用FJM，节理部分颗粒间接触采用SJM，采用标准圆柱形试件，试件高为100 mm，直径为50 mm，最小颗粒半径为0.5 mm，颗粒半径比Rmax/Rmin设置为1.66，共生成15 268 个颗粒；本文设置节理间距为10 mm，共7 个倾角(0°，15°，30°，45°，60°，75°和90°)，岩体试件数值模型如图1所示。

基于不同倾角的横观各向同性岩体数值模型进行数值单轴压缩试验，获取宏观参数。细观参数采用上文中标定参数指标体系，通过试错法选取一套基准细观参数如表1所示，将细观参数输入数值模型，获得岩体抗压强度与弹性模量的关系，如表2所示，节理宏观法向刚度为8 196.72 GPa/m，节理宏观切向刚度为3 039.51 GPa/m。

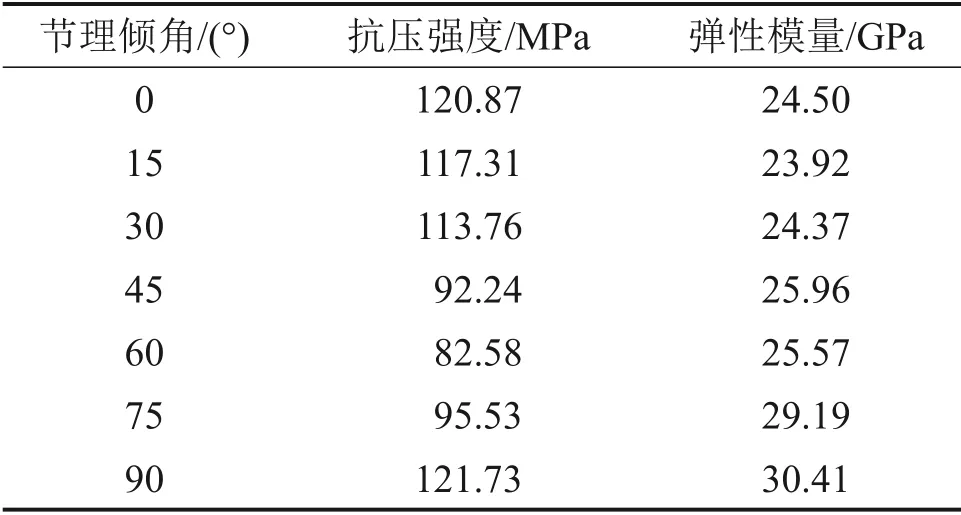
表2 数值模型宏观参数Table 2 Macroparameters of numerical models

2.1 FJM模型细观参数敏感性与强度比确定

参数标定的关键步骤是获取细观参数对宏观参数的影响。吴运杰等[27-30]采用平直节理模型(FJM)模拟岩土体力学性质，发现c*和σc*为影响宏观抗压强度的显著因素，E*为影响宏观弹性模量的显著影响因素。吴运杰等[27-28]通过正交试验得到岩石压拉比的显著影响参数为强度比c*/σc*。为获取岩石宏观压拉比σc/σt与细观参数强度比c*/σc*的函数关系，本文基于图1所示的数值模型，开展控制变量实验，实验结果及拟合曲线如图2所示。

本文以典型横观各向同性岩体即页岩为例进行细观参数标定。石妍茹等[31]对不同含水状态的泥岩进行单轴压缩试验和巴西劈裂试验，得到泥岩的压拉比范围为6～7；李昌进等[32]研究泥岩相似材料的强度与填筑形式，得到相似材料的压拉比为7～8。参考前人研究结果，本文将完整岩石的压拉比设置为7，由拟合公式得到细观参数强度比c*/σc*为2.2。

2.2 SJM模型细观参数敏感性

在建立完整岩石基础上，采用SJM 添加平行节理获得横观各向同性岩体。基于选定的基准参数，采用控制变量法进行单轴压缩数值试验，分析细观参数敏感性，SJM细观参数取值范围如下：kn为50～590 GPa/m；ks为1 000～8 500 GPa/m；μ为0.5～0.7；σc为2～30 MPa；c为10～40 MPa；d为0.4～0.9 mm。

2.2.1 宏观单轴抗压强度与弹性模量敏感性分析

为进一步分析各细观参数的影响规律，将kn和ks划分为细观变形参数，将σc，c和μ划分为细观强度参数，并单独讨论d。不同细观参数下横观各向同性岩体宏观参数随节理倾角的变化曲线分别如图3～5所示。由图3～5可见：随着节理倾角增加，单轴抗压强度和弹性模量曲线呈现先下降再上升的U 形，单轴抗压强度最小值出现在节理倾角为60°附近，弹性模量最小值出现在节理倾角为15°附近。

d是节理宏观参数的重要影响因素，它通过改变节理宏观刚度与细观刚度的比(Kn/kn和Ks/ks)直接影响节理性质[23]。如图3所示，在相同节理倾角条件下，d与单轴抗压强度、弹性模量呈现负相关的趋势，证明节理对岩体的劣化效应随厚度增大逐渐增加。

对于细观变形参数，kn对强度和弹性模量的影响随着节理倾角增加逐渐减小，对含90°节理的岩体强度几乎不产生影响(图4(a)和(b))，证明随着kn逐渐减小，节理对含小节理倾角的岩体强度的劣化作用更为明显；ks对抗压强度不产生规律性影响，为降低标定复杂性，在后文抗压强度标定过程中忽略ks的影响(图4(c))，ks对弹性模量的影响随着节理倾角增加逐渐增大，对含0°节理的岩体弹性模量几乎不产生显著性影响(图4(d))。

对于细观强度参数，c与抗压强度呈正相关关系(图5(a))；σc对0°和90°试件的抗压强度不产生显著影响，其余倾角试件的抗压强度呈正相关关系(图5(b))，但是σc过小会导致90°倾角岩体强度急剧下降；μ对抗压强度不产生显著影响(图5(c))。细观强度参数均对弹性模量不产生显著影响，文中不再展示。

2.2.2 宏观节理刚度影响因素分析

基于最小二乘法，在三维条件下计算得到不同工况下的节理宏观刚度，如图6所示。为方便展示，将各个细观参数进行标准化处理。由图6得到d作为影响节理性质的重要因素，与宏观刚度参数呈现非线性负相关关系。同时，细观变形参数(kn，ks)也是影响节理宏观刚度(Kn，Ks)的主要因素，其中kn与Kn和Ks都呈正相关关系，ks与Kn呈负相关关系、ks与Ks呈正相关关系。同时，细观强度参数对节理宏观刚度无显著影响。

3 细观参数标定方法

双模型细观参数叠加导致宏观-细观参数对应关系复杂，造成标定困难，这需要梳理各参数的优先级，形成优先级体系，按照重要程度依次进行标定；不同模型之间的参数不是独立的，需要考虑不同模型参数的联系，而非依次标定。

3.1 宏细观参数函数表征体系

XIA 等[23,33]研究表明，优先研究含0°和90°节理岩体的宏细观参数会大幅减小工作量，细观变形参数对弹性模量和抗压强度产生影响，细观强度参数只对抗压强度产生影响。所以，依次通过抗压强度标定细观强度参数，通过弹性模量标定细观变形参数是可行的。

首先，对SJM 细观参数进行分析，对于宏观弹性模量，E90的显著影响参数为d和ks；宏观刚度(Kn和Ks)的显著影响参数为d，ks和kn。对于宏观强度参数，完整岩石强度σ是含节理岩体强度σθ不可忽略的影响因素，所以σ作为影响参数加入宏观强度参数的讨论。σ90的显著影响参数为d，σ和c；σ0的显著影响参数为d，kn，c和σ。按照上述宏观参数顺序，对其相应的细观参数进行逐步标定，形成标定参数优先级。采用矩阵表示SJM 细观参数标定优先级，如式(2)所示。

最后，对FJM 参数进行讨论，由敏感性分析得到E的显著影响参数为E*，σ的显著影响参数为σc*(c*)，采用矩阵表示如下：

横观各向同性岩体σθ和Eθ的显著影响因素中，完整岩石的力学参数E和σ是不可忽略的，所以FJM 细观参数、完整岩石宏观参数、含节理岩体宏观参数、SJM 细观参数存在递进影响关系。因此，通过完整岩石的宏观力学参数沟通双模型的细观参数，解决双模型细观参数相互影响的问题，这是可行的。由式(1)得到90°倾角条件下E90与E数值相同，E*是完整岩石E的决定性影响因素，所以在90°倾角下，E*也就是E90的决定性影响因素；σc*(c*)是完整岩石强度σ的决定性因素，完整岩石强度σ又是横观各向同性岩体强度σθ的显著影响因素，因此，σc*(c*)是σθ的影响因素。采用上述理论联系双模型参数，基于式(2)和(3)，建立FJM 和SJM 全参数标定优先级，构建宏细观参数函数表征体系，见式(4)～(9)。

3.2 细观参数迭代修正方法

在标定横观各向同性岩体时，基于宏细观参数表征体系，对细观参数进行初步计算，得到基准参数值，将细观参数输入PFC3D数值模型进行单轴压缩实验，获取宏观力学响应后与物理实验值进行对比，在相对误差大于3%时，对各公式进行迭代修正。

为确定各步骤单变量函数关系，进行数值实验，结果如图7所示，可见宏观参数与细观参数呈线性关系，证明采用一次函数对细观参数进行迭代修正是可行的。基于一次函数得到迭代公式(式(10))及终止条件(式(11))如下：

式中：ΔX(k)为第k次迭代过程中实际宏观参数与数值模型获得宏观参数值的差值；x(k)表示第k次迭代细观参数；φ为迭代步长。

3.3 横观各向同性岩体细观参数标定方法

依据宏细观参数函数表征体系和细观参数迭代修正方法，提出一套标准化横观各向同性岩体细观参数标定流程，如图8所示。

首先，对与0°和90°节理岩体相关的细观变形参数进行标定，如步骤1)～步骤5)，再进行一次迭代修正步骤6)；

然后，对与0°和90°节理岩体相关的细观强度参数进行标定，如步骤7)～步骤8)，再进行一次迭代修正步骤9)；

最后，通过15°～75°倾角岩体标定其余参数，如步骤10)。

4 案例分析

为验证本文提出的双模型横观各向同性岩体细观参数标定方法(CM-FJM&SJM)，根据实验室压缩试验获得的页岩宏观参数[23]，如表3所示，节理宏观法向刚度为4 174 GPa/m，节理宏观切向刚度为2 438 GPa/m。

为获取横观各向同性岩体宏细观参数函数表征体系，需要对各公式的主要影响参数进行实验，通过最小二乘法获取回归公式系数，其中，式(4)为单变量函数，设计控制变量实验，采用一元一次函数进行拟合，剩余公式需要设计正交实验，采用多元一次函数进行拟合，达到了良好的拟合效果。具体过程如图9所示。

本文采用物理实验获取的页岩宏观力学参数作为参考标定对象，验证提出的标定方法。标定步骤如下：

1)细观变形参数标定。基于物理试验获取标定所需宏观参数σθ，Eθ，Kn和Ks，如表3所示。由式(4)计算得到E*=35 GPa。设置d的精度为0.1 mm，通过式(5)得到一系列d和ks组合，d1为0.65，0.75 和0.85 mm 时，ks分别为7 876，7 976和8 076 GPa/m。由式(6)得到d=0.65 mm时，kn不符合条件，删除此组参数，计算可得当d为0.75 mm 和0.85 mm 时，kn2分别为204 GPa/m 和7 976 GPa/m；kn3分别为763 GPa/m和7 976 GPa/m。由式(7)得到d=0.75 mm。

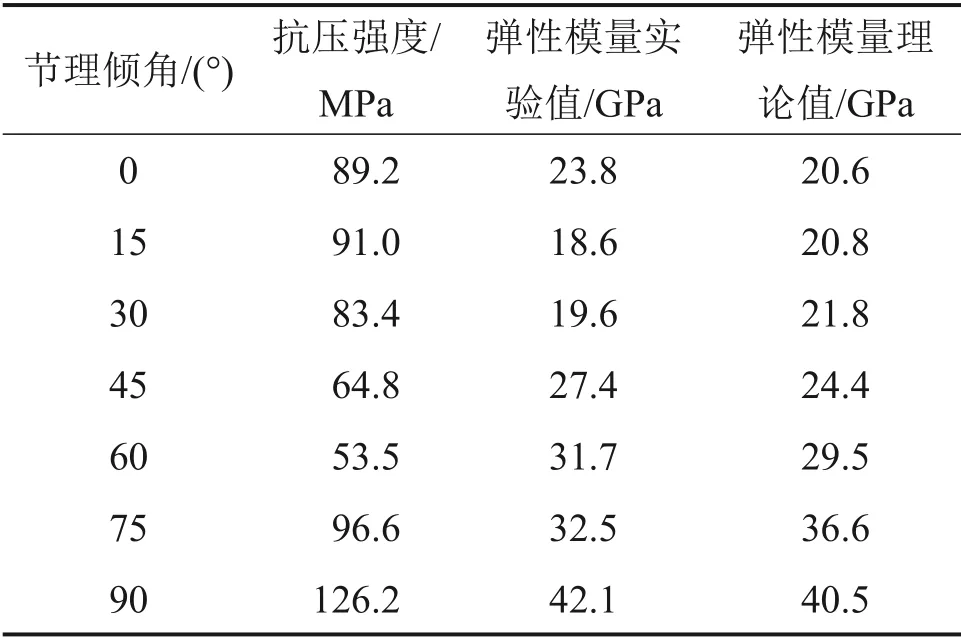
表3 实验室获取的页岩宏观参数Table 3 Macroscopic parameters of shale obtained in laboratory

2)迭代修正。将上述计算得到的初步细观参数，E*=35 GPa，d=0.75 mm，kn=204 GPa/m，ks=7 976 GPa/m，输入PFC3D开展数值压缩实验，其余还未标定的细观参数采用表1中数据，获得岩体宏观变形参数E90为40.63 GPa，Kn为4 032.26 GPa/m，Ks为2369.67 GPa/m。检查与岩体宏观变形参数是否复合相对误差要求，发现宏观参数Kn相对误差大于3%，不符合要求，需要进行迭代修正，迭代系数为2.1，计算得到kn为271 GPa/m。将上述修正后的参数再次输入PFC3D开展数值压缩实验，得到E90为40.73 GPa，Kn为4 166.67 GPa/m，Ks为2 398.08 GPa/m。宏观参数符合相对误差要求，接受此组参数。

3)细观强度参数标定。设置σc*精度为5 MPa，

由式(8)得到=24 MPa，c1=68.5 MPa；=29 MPa，c2=25.13 MPa；=34 MPa，c3=-18.27 MPa。由式(9)计算得到σc*=29 MPa。4)迭代修正。将上述参数输入PFC3D开展数值压缩实验，获得岩体宏观强度参数σ0为91.68 MPa，σ90为125.37 MPa。宏观参数符合相对误差要求，不进行迭代。

5)剩余参数标定。调整σc使横观各向同性岩体强度与参考宏观参数相关系数达到最大值。采用上述步骤得到的细观参数作为基准值，采用控制变量法获取相关系数如图10所示，结果表明在σc大于10 MPa后相关系数不再上升，所以选定σc=10 MPa。

将采用CM-FJM &SJM 获得的宏观参数，并与实验室结果进行比较，结果如图11所示。单轴抗压强度数值实验结果与室内实验结果的相关性系数为94.01%，而弹性模量的数值实验结果与室内实验结果的相关性系数为94.24%。

将采用CM-FJM &SJM 获得的破裂模式与实验室结果进行比较，如图12所示，PARK 等[33]的试验结果表明，随着倾角增大，软弱面对岩体破坏的作用逐渐增强，破裂面逐渐由完整岩石部分向节理面转移。由此可见，本方法适用于基于FJM 和SJM 建模的含平行结构面岩体的细观参数标定，能够得到宏观参数，同时本方法能较好地模拟破裂过程中节理对岩体强度的劣化作用。

5 结论

1)通过参数简化，形成了横观各向同性岩体标定参数指标体系，基于指标体系分析了参数敏感性，得到宏细观参数影响关系，获取了完整岩石宏观参数的显著影响参数为平直节理模型中的有效模量和细观强度参数。

2)0°和90°节理岩体宏观变形参数的显著影响参数为光滑节理模型中的节理厚度、法向刚度和切向刚度，宏观强度参数的显著影响参数为光滑节理模型中的节理厚度、法向刚度和切向强度。

3)通过FJM模型细观参数-完整岩石宏观参数-横观各向同性岩体宏观参数-SJM 细观参数之间递进的影响关系，以完整岩石和横观各向同性岩体的宏观参数为桥梁，沟通FJM和SJM细观参数，使得双模型参数可以共同参与标定优先级的建立，解决了模型内和模型间的细观参数共同影响同一宏观参数，导致细观参数相互干扰的问题。

4)基于敏感性分析得到的宏细观参数显著影响关系，依据影响各宏观参数的细观参数数量，形成了FJM 和SJM 全参数标定优先级，确定细观参数标定顺序，构建了宏细观参数函数表征体系，解决了双模型细观参数数量多，导致宏观-细观参数对应关系复杂的问题。

5)基于宏细观参数函数表征体系，给出了一套针对于横观各向同性岩体的标准化细观参数标定方法(CM-FJM&SJM)。将本方法应用于页岩进行验证，数值模型得到的强度和弹性模量参数与实验室结果相对误差小于3%，证明本文提出的标定方法是有效可靠的。