横风作用下悬挂单轨车桥系统动力响应研究

邹云峰，刘志鹏，史康，何旭辉，周帅，汪震

(1.中南大学土木工程学院，湖南长沙，410075；2.轨道交通工程结构防灾减灾湖南省重点实验室，湖南长沙，410075；3.重庆大学土木工程学院，重庆，400045；4.中国建筑第五工程局有限公司，湖南长沙，410007)

悬挂式单轨交通作为一种新兴的城市轨道交通形式，具有通行能力强、安全可靠、占地面积小等特点，可作为中运量或短途、低运量的轨道交通首选方式，能够有效缓解日益突出的城市交通拥堵问题[1]。悬挂式单轨交通系统已在德国和日本运营多年，我国目前仍处于发展阶段，在多地相继开展规划并建成试验线，具有广阔的应用前景。现有研究表明，横风作用对车辆运行安全性和舒适性的影响显著，而车辆的驶入和驶离也会对桥梁的气动特性产生明显影响[2-3]。由于悬挂单轨车桥系统中车辆运行于桥梁下方，导致风荷载作用下车辆和桥梁的动力问题更加突出[4-7]，但相关的研究报道较少。因此，研究横风作用下悬挂单轨系统的动力响应具有重要的意义。关于悬挂单轨车桥系统，目前的研究主要集中在动力性能方面。曹恺[4]基于ADAMS建立了悬挂单轨车辆的动力学仿真模型，对车辆悬挂参数进行优化，并对参数优化后的车辆动力学性能进行了预测；CAI等[5]基于多体动力学和有限元理论建立了悬挂单轨车桥系统的耦合模型，用于研究其动力特性；何庆烈等[8-9]针对我国第一条悬挂式单轨交通试验线开展了行车动力学试验，得到了车辆和桥梁详细的动力性能实测结果，并对悬挂单轨车辆的曲线通过性能和桥梁的振动特性进行了计算和分析；JIANG 等[10]采用FIALA 公式建立了轮胎模型并通过ANSYS 和UM 联合仿真对悬挂式单轨车桥耦合系统共振问题进行了研究。以上研究成果对分析悬挂单轨系统自身的动力性能提供了很好的参考，对工程实际具有重要的指导意义。目前，关于风荷载对车桥系统动力性能的影响的研究很少，既有文献仅有BAO 等[6]采用数值模拟方法对悬挂单轨车辆交会时风-车-桥耦合系统的气动性能和振动特性进行了研究，然而，该研究缺乏系统性的风洞试验来揭示悬挂单轨车桥系统的气动耦合特性，并缺乏横风对行车安全性的影响研究。相对数值模拟，风洞试验方法则更加直接、有效，得到的气动力系数可直接应用于风荷载作用下的车桥系统动力响应分析。为此，本文采取风洞试验与数值仿真相结合的方式，探讨横风作用下悬挂单轨车辆和桥梁的气动特性以及车速和横风风速对车辆和桥梁动力响应的影响规律，并以车辆运行安全性评判指标为标准，给出横风作用下悬挂单轨车桥系统安全运营的临界风速。

1 车桥耦合系统动力模型

1.1 车辆多刚体模型

悬挂单轨车辆是由车体、构架、轮对和悬挂装置等构成的复杂多体系统，本文对其进行适当简化，将单节车辆视为由1个车体、2个转向架(含摇枕、中心销和悬挂装置)、4个走行轮对和8个导向轮组成的质量-弹簧-阻尼系统，通过刚体(rigid body)和力元(force element)进行模拟。车辆不同构件相互联系构成了整体运动关系，车体的垂向和横向运动均受到悬吊装置、构架和走行轮等的限制，转向架也因导向轮在桥梁内部运行而被限位，因此，建立模型时每个车体和构架仅考虑横摆(y)、沉浮(z)、点头(β)、摇头(γ)和侧滚(α)5 个自由度，忽略纵向伸缩自由度(x)，对车轮和转向架上的摇枕、中心销和悬挂装置的自由度也进行简化，最后建立具有41 个自由度的车辆多刚体模型[11]，拓扑结构如图1所示。其中，数字0 和6 分别表示构建之间连接的自由度个数。

需注意的是，悬挂单轨车辆采用的是橡胶轮胎，而车轮是实现车辆和桥梁之间动态位移和作用力传递的构件，是正确建立模型的关键。由于橡胶轮胎的结构和力学特性复杂，在多体动力学模型中直接建立轮胎模型十分困难，故需要对轮胎模型进行简化。现阶段常用的轮胎模型有Pacejka 模型、Fiala 模型、Sakai 模型和Frank 模型等[12]。Pacejka 模型将轮胎变形视为张紧的弦，在驱动和制动状态下具有联合侧偏特性，得到了广泛使用。本文走行轮选用Pacejka模型进行模拟[12]。由于导向轮的轮胎侧偏角在直线和小半径曲线仿真过程中对结果几乎不产生影响，故在建立模型时只需考虑导向轮的径向作用，采用弹性阻尼并联的弹簧力元模拟[13]。

将建立的车辆模型按照文献[14]进行参数和工况设置，在曲线线路上运行时，轮胎径向力时程曲线如图2所示，导向轮和走行轮径向力变化趋势均与文献[14]中的一致。表1所示为本文轮胎径向力与文献[14]中径向力的比较，最大相对误差只有7%，验证了本文车辆模型的正确性。

表1 轮胎径向力最大值与文献[14]中的值对比Table 1 Comparison of the maximum radial forces of tire with those from Ref.[14]kN

1.2 桥梁有限元模型

据文献[15]选取桥梁结构关键部位的设计参数，采用有限元软件ANSYS建立悬挂单轨系统的桥梁模型。桥梁的单跨跨径为30 m，在距离梁端0.5 m处布置横向加劲肋，中间间隔1.5 m，具体构造如图3所示，支座处的约束条件[11]如表2所示。

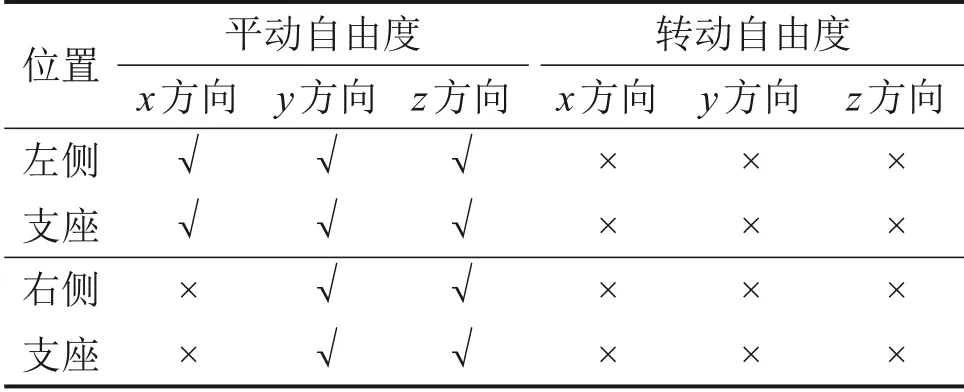
表2 桥梁边界条件Table 2 Boundary conditions for the bridge

针对悬挂式单轨桥梁的特点，采用ANSYS 中的SHELL63 单元建立有限元模型。将结构划分成一系列壳单元组合，在各个壳单元内部选择恰当的插值或位移函数模式，分别计算每个单元的动能、应变能以及整个结构的总动能和总应变能。由拉格朗日表达式建立桥梁结构的动力学方程，最后利用直接积分法或模态叠加法对结构动力响应求解。

对已建立的桥梁有限元模型进行模态分析，得到模型的前2 阶弯曲振型如图4所示。表3所示为模态计算结果与文献[15]中结果的比较，可见两者具有较好的一致性。

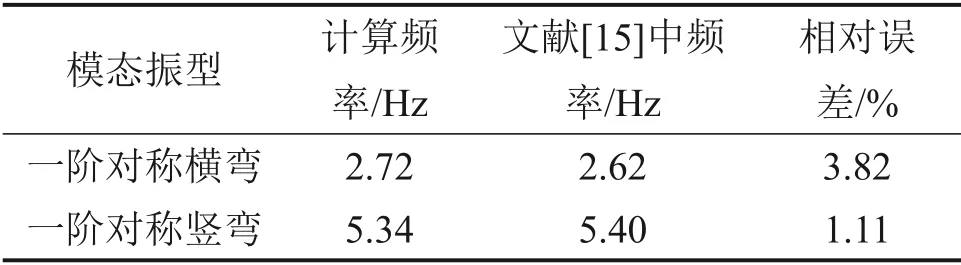
表3 桥梁前2阶弯曲振型及频率Table 3 The first two bending modals of bridge

1.3 车桥系统交互模型

悬挂单轨车桥系统由车辆子系统和桥梁子系统组成。首先根据设计参数在ANSYS中建立有限元模型，再进行子结构分析，得到包含桥梁质量矩阵和刚度矩阵的*.sub 文件和包含桥梁几何信息的*.cdb 文件。然后，通过多体动力学软件SIMPACK 的有限元接口程序FEMBS 调用文件，生成弹性桥梁输入文件*.fbi。车辆模型由SIMPACK 直接建立，与导入的弹性桥梁通过轮轨数据交换前处理程序进行数据交换，实现车-桥耦合振动的动力学仿真模拟[16]。基于SIMPACK 和ANSYS 联合仿真的车-桥耦合分析流程如图5所示。

在车桥耦合动力相互作用下，悬挂单轨车辆经过桥梁时会引起桥梁结构产生振动和变形，桥梁的振动和变形反过来又会影响车辆的运行安全性和舒适性。而横风作用是影响行车安全性和舒适性的关键因素之一[17]，有必要对横风作用下悬挂单轨车辆和桥梁的动力响应进行评价。由于目前国内没有规范对悬挂单轨车桥系统的动力响应指标作出明确规定，本文根据文献[11]给出的部分评价指标对悬挂单轨车桥系统的动力性能进行初步分析，具体选用的车辆和桥梁评价指标如表4所示。

表4 悬挂单轨车桥系统动力性能评判标准Table 4 Evaluation criteria for dynamic performance of SMVB system

2 车桥耦合系统风荷载模拟

2.1 车辆与桥梁气动特性

作用在车辆和桥梁上的风荷载包括平均风引起的静风力、脉动风引起的抖振力以及结构与流体之间产生的自激力。由于本文中模型较钝，宽度较小，不考虑车辆和桥梁受到的自激力作用[7]。车辆和桥梁的气动力系数由风洞试验测得，试验在均匀流场中进行，风速为12 m/s[19-20]，风洞试验照片如图6所示，风速谱如图7所示，测得的阻力系数CD、升力系数CL和力矩系数CM均值如表5所示。由表5可知：车辆和桥梁的阻力系数非常接近，但由于车辆模型的高度更大，所受的阻力大于桥梁所受的阻力；车辆和桥梁的升力系数正负相反，这是因为车辆和桥梁受到的升力方向相反。升力矩是阻力和升力共同作用的结果，力矩系数接近于0，与阻力系数和升力系数相比，其影响可以忽略不计。不难发现，车辆和桥梁的三分力系数中，阻力系数最大。由试验模型的尺寸特征可知，车辆和桥梁主要受到的是阻力作用，需要注意加强桥梁的横向刚度和车辆的抗侧滚能力。

车辆的平均风压系数和脉动风压系数分别如图8(a)和图8(b)所示。从图8(a)和图8(b)可见：迎风面AB和BC上的平均风压系数先增大而后略减小，在BC面中心处达到最大；背风面DE和EF以及底面CD上的平均风压系数几乎没有变化。由于峡谷效应[21]的影响，顶面AF的平均风压系数明显增大，其中，32 号测点处的平均风压系数增大最显著。从图8(b)可以发现：车辆的脉动风压系数在迎风面AB和BC面上几乎不变，且接近为0，而在底面CD和背风面DE和EF有明显波动，尤其在顶面31 号测点处脉动风压系数达到最大，这是因为上部桥梁改变了绕流，导致风压变化显著。桥梁的风压系数见图8(c)和图8(d)。从图8(c)可以看出：迎风面AB上1～5 号测点的平均风压系数因车辆干扰略有增加，此外，测点6和7的平均风压系数从-1.0明显增加到-2.0，其主要原因是车辆和桥梁模型之间存在一定间隙。由于峡谷效应，间隙很容易对BC面的风压产生放大效应。CD面和AD面的平均风压系数变化较小。就脉动风压系数而言，AB面上的脉动风压系数很小且基本保持不变，BC面的脉动风压系数受峡谷效应影响显著增大，CD面脉动风压系数则又减小。15 和16 号测点的AD面脉动风压系数呈下降趋势，而第17到第19号测点的脉动风压系数基本保持稳定。

2.2 车桥系统风荷载的实现

车辆和桥梁所受风荷载遍布结构表面各处，但在动力学仿真中无法据此施加风荷载，为此，将简化的气动力作为车辆和桥梁的动力激励输入，在SIMPACK中通过力元(force element)连接标记点(marker)的方式实现风荷载加载[22]。在车辆质心位置和桥梁顺桥向节点处建立风荷载作用标记点。需要注意的是，由于车辆运行时质心位置会发生变化，因此，需要在全局坐标系中建立跟随车体运动的移动标记点。而桥梁上的标记点是沿顺桥向方向间隔一定距离进行设置[23]，本文中，每隔3 m在桥梁上定义1个标记点，用于施加风荷载。

气动力计算公式为[24]：

式中：FD(t)，FL(t)和MT(t)分别为阻力、升力和力矩；CD(t)，CL(t)和CM(t)分别为阻力系数、升力系数和力矩系数，通过风洞试验测得；ρ为空气密度；U为模型高度的来流风速；D1为模型特征高度；B1为模型特征宽度；l0为特征长度，对于车辆，l0=14.8 m，对于桥梁，l0=3.0 m(每3 m 设置1个风荷载作用点)。

风荷载的施加包括加载、持续和卸载3 个过程。本文中设置加载时间为5 s 作为过渡段，以减小风荷载施加到车桥系统产生的冲击作用。风荷载沿横桥向垂直作用于车体和桥梁，加载过程如图9所示。

3 车桥耦合系统动力响应

3.1 车辆速度的影响

参考成都悬挂单轨试验线的最高运行速度65 km/h，为充分考虑车辆速度对该车桥系统动力响应的影响，采用直线线路，并施加美国6级谱轨道不平顺。车速范围为50～70 km/h，步长为5 km/h。风荷载由第2 节中风洞试验生成，风速为15 m/s。为便于观察风荷载的影响，还给出未施加风荷载作用时的响应结果。车辆和桥梁的响应随车速变化结果分别如图10和图11所示。

从图10(a)可以看出：在横风作用下，导向轮和走行轮的最大径向力随车速变化并不明显，在各车速下，走行轮最大径向力均满足行车安全性要求；导向轮的最大径向力小于走行轮的最大径向力，这是因为本文计算模型为直线线路，在风荷载较小时，车辆主要承受垂向荷载；与无风荷载时相比，在不同车速下，走行轮和导向轮的径向力均有较小幅度提升。从图10(b)可见：车体的横向加速度和竖向加速度均随着车速增加而增加，在车速为70 km/h时，横向、竖向加速度最大值分别为0.86 m/s2和0.80 m/s2，均满足限值要求。不难发现，随着车速增加，横风作用对车辆振动加速度的影响更加显著，尤其是横向加速度，其值超过了竖向加速度，最大增幅达到无风荷载时加速度的7倍多，在实际运行时，需加强车辆和桥梁的横向稳定性。从图10(c)可以看出：随着车速增大，竖向Sperling 指标有增大趋势，但最大仅为1.3，横向Sperling 指标最大值为1.8，两者均小于2.5，车辆舒适性指标为“优秀”。显然，横风主要导致横向Sperling指标大幅度增加，这与图10(b)中结果一致。由图10(d)可知：横风极大地加剧了车体侧偏程度，随着车速增加，车体侧偏角逐渐加大，最大达到了6.4°，虽然未超出7.5°的限值，但明显对行车不利；而在无风荷载时，车体侧偏角随车速增加虽有所增加，但因为车辆直线行驶，车体侧偏角最大仅为0.22°。由此可知，需要增大横风作用下车辆的抗侧滚能力。

从图11(a)可以看到：桥梁跨中横向位移和竖向位移受车速的影响均比较有限，在不同车速下，桥梁的横向位移在11.6 mm 左右波动，最大为12.0 mm，最大挠跨比为1/2 500；竖向位移在23.8 mm 左右波动，最大为24.0 mm，最大挠跨比为1/1 250，均符合限值要求。显然，横风主要导致桥梁横向位移响应大幅度增加，达到无风时的2倍多，而对竖向位移响应的影响几乎可以忽略。从图11(b)可知：桥梁的振动加速度随车速的变化较明显，总体上呈现随车速增大而增大的趋势，但均未超过限值。横风作用时，桥梁的横向加速度比竖向加速度对车辆运行产生影响更大，这与图10(b)中车辆振动加速度的规律是一致的。

3.2 横风风速的影响

为充分考虑横风风速变化对悬挂单轨车桥系统的动力响应影响，选取风速范围为5～25 m/s，步长为5 m/s，考虑车辆速度为65 km/h在直线线路运行的情况，采用美国六级谱轨道不平顺，对不同横风风速下的车桥系统动力响应进行计算分析。为便于观察与无风荷载时的动力响应区别，还给出未施加风荷载时该车速下的响应结果。车辆和桥梁的响应随横风风速变化结果分别如图12和图13所示。

从图12(a)可以看到：随着风速增加，走行轮和导向轮的最大径向力逐渐增大，在所选风速范围内，走行轮最大径向力始终满足行车安全性要求。与无风荷载时相比，横风风速越大，走行轮和导向轮的径向力增加越显著。需要注意的是，过大的径向力会加速轮胎磨损，影响车辆运行。从图12(b)可知：车体的横向和竖向加速度受横风影响明显，两者均随风速增加而增加；当风速小于15 m/s 时，车体加速度增幅较小，而当风速大于20 m/s 时，车体加速度显著增大；当风速为25 m/s 时，车体横向和竖向加速度均超出限值要求，此时，应对车辆进行限速或视具体情况停运。从图12(c)可见：随着横风风速增加，车辆的横向和竖向Sperling 指标均明显增大，行车舒适性降低；当风速为25 m/s时，横向Sperling指标达到最大，为2.46，竖向Sperling 指标为1.93，两者均属于“优秀”。显然，横风对横向Sperling 指标影响更加显著，这与图10(c)中结果是一致的。从图12(d)可知：随着风速增加，车体侧偏角显著增大；当风速达到20 m/s时，车体侧偏角为8.9°，超出限值要求，此时，行车安全有待加强，应视情况进行限速或停运，以确保行车安全。

从图13(a)可见：桥梁跨中位移随风速增大而增大，尤其是跨中横向位移增幅显著。这是因为风速增大不仅导致桥梁所受风荷载增大，而且带有横向风压的移动车辆也会对桥梁产生动力作用。由桥梁气动力可知，桥梁所受阻力显著大于升力，这也解释了桥梁跨中横向位移增幅大于竖向位移增幅的原因。当风速为25 m/s 时，桥梁跨中横向和竖向位移均达到最大，分别为23.0 mm 和24.6 mm，对应的挠跨比分别为1/1 304 和1/1 220，均满足限值要求。从图13(b)可见：桥梁横向和竖向加速度均随风速增加而增加，且横向加速度增幅显著大于竖向加速度增幅；当风速小于10 m/s时，桥梁竖向加速度大于横向加速度；相反，当风速大于15 m/s时，横向加速度大于竖向加速度，此时，车辆运行主要受到桥梁横向加速度的限制。

4 结论

1)横风作用会导致车辆和桥梁的动力响应大幅度增加。由于车辆和桥梁受到的气动力均以阻力为主，导致车辆和桥梁的横向响应增幅大于竖向响应增幅，需要注意加强桥梁的横向刚度和车辆的横向稳定性。

2)在横风作用下，车辆速度增大会导致车辆的动力响应呈增大趋势，但增大幅度有限，其中，以车体侧偏角增大最明显，最大达到6.4°，显然对行车舒适性不利，需要增大车辆的抗侧滚能力。车辆速度增大同样会导致桥梁的动力响应增大，但均未超过限值要求。

3)随着横风风速增加，桥梁的动力响应满足限值要求，但当风速达到20 m/s 时，车体侧偏角达8.9°，超过限值要求，影响到行车安全；当风速达到25 m/s 时，车辆的横向和竖向加速度均已超出限值，行车安全性和舒适性均不符合要求。因此，当风速达到15～25 m/s时，建议对车辆进行限速或视具体情况停运；而当风速超过25 m/s 时，建议停止车辆运行。