基于TOF相机的超近程空间非合作目标的位姿估计

姜丽辉， 郑循江， 杨逸峰， 赵 旸， 张徐玮， 孙朔冬

上海航天控制技术研究所,上海 201109

0 引 言

从20世纪60年代太空时代开始，地球轨道上的人造飞行器就开始急剧增加，包括已经使用过的火箭残骸、爆炸产生或者碰撞产生的碎片、失效或者失控卫星等.这些失控人造空间残骸的运动状态又是各有不同，可能高速运动、高速原地旋转或者静止，而绝大部分是高速运动状态.随着现在人类空间活动的急剧增加，一是该类空间残骸在急剧增加，占用着十分珍贵的地球轨道资源；二是该类空间残骸也威胁着后续正常的人类空间活动，对后续的飞行器有着不可预知的威胁.针对这一问题，除了利用各个国家应该遵守的国际空间法规约束各国空间活动外，通过科学技术途径主动去解决该问题的研究也在近几年活跃起来，主要包括了在轨服务(OOS)任务，主动空间碎片清除(ADR)任务等[1-2]，实现该类空间活动必须使空间飞行器具备高度的自主能力，在轨高度自主完成相应任务，尽可能减少地面人员干预.因为该类任务需要飞行器超近距接近空间非合作目标去执行高风险的高机动动作，由于地面无线通讯的延迟以及存在通讯无法覆盖的通讯盲区区域，无法做到地面实时操控干预，因此需要一套高度自主制导、导航与控制系统(GNC)在轨自主完成以上任务.本文主要关注超近程的相对位姿测量问题，因为不管是在轨服务(OOS)还是主动空间碎片清除(ADR)任务，目标都是不可控的且无法与目标进行通讯获取其姿态信息，因此必须通过光电传感器比如被动传感器双目相机、主动传感器激光雷达去获取目标的实时运动状态信息[3].现有公开文献关于超近程相对位姿测量方案包括了多种传感器组合以及不同算法方案策略，后续在该问题上的解决方案在硬件配置上应该是多传感器冗余配置、融合使用的趋势，该方案可以融合不同体制传感器的优势，同时可以进行不同体制进行相互备份，保证在近程执行任务过程的稳定可靠.利用不同传感器进行冗余配置进行数据融合获取目标相对位姿应用主要包括两种方案，第一种方案是将原始数据(包括2D图像数据以及3D点云数据等)根据目标的纹理结构以及安装几何约束，在原始数据层面进行融合，构建位姿解析框架，获取目标相对位姿，比如近几年比较热门的人工智能方向，利用多源数据构建姿态估计学习网络框架，通过训练以及学习获取可用网络结构，应用该网络进行回归获取目标相对位姿；第二种方案是分别利用不同的传感器获取目标的姿态，根据不同传感器的应用环境以及误差特性，将获取的相对姿态融合(比如构建卡尔曼滤波器)获取最终的目标姿态.本文主要说明利用新体制传感器TOF相机进行超近程位姿测量的问题[4-6]，该体制相机可以同时获取目标的二维灰度与三维点云数据，因此提出融合目标二维灰度信息与三维点云信息的位姿估计算法框架，采用基于弧段的椭圆提取方法和ICP点云迭代方法求解非合作目标的相对位姿信息，该算法框架同时弥补了二维灰度图像缺少深度信息的不足和三维点云数据缺少目标纹理特征信息的不足，同时结合卡尔曼滤波跟踪算法，确保基于TOF相机的非合作目标相对位姿解算稳定可靠.

1 TOF相机

1.1 TOF技术原理

TOF是通过主动发射调制激光，经目标表面反射到探测器后解调探测器与目标之间光的飞行时间，最终获取目标的距离的技术.根据测量时间的方式不同，该技术可分为脉冲式、连续波式、伪随机数序列式以及压缩感知式等多种不同飞行时间测量系统[5].本文采用的连续波式飞行时间系统，测距原理图1所示，其中黑色波形为激光器发射调制波，红色波形为经目标反射进入探测器波形，Δφ为反射激光与回波激光的相位差，探测器通过解调获得该变量，最终利用式(1)获取目标点的距离信息，其中z表示目标深度、c为光速、ω为激光调制频率.

(1)

1.2 TOF相机组成

根据TOF技术原理设计本文使用的TOF相机，相机组成框架示意图如图2所示，主要由远场光学系统以及对应激光器和探测器、近场光学系统以及对应探测器和激光器、图像采集与信息处理模块、供电模块以及接口模块组成.如图3为相机产品示意图，其中远近双视场设计是为了满足目标由远及近(100～1.5 m)逼近过程中进行全程位姿测量，图像采集与信息处理模块则完成探测器驱动、图像采集与解调、位姿解算以及对外通信功能.

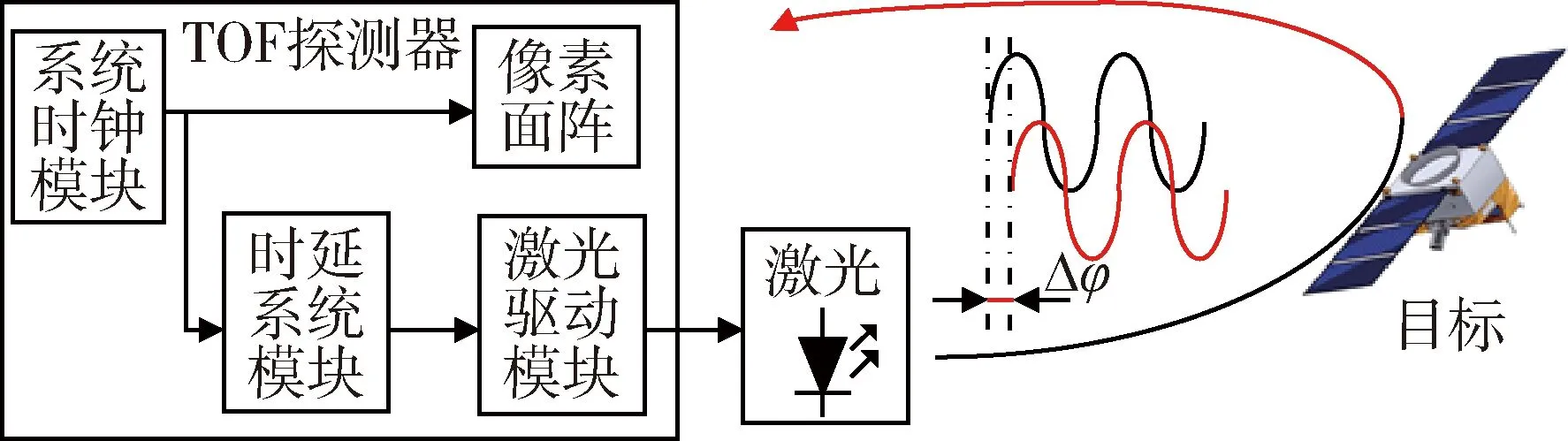
图1 TOF相机原理示意图Fig.1 Schematic diagram of TOF camera principle

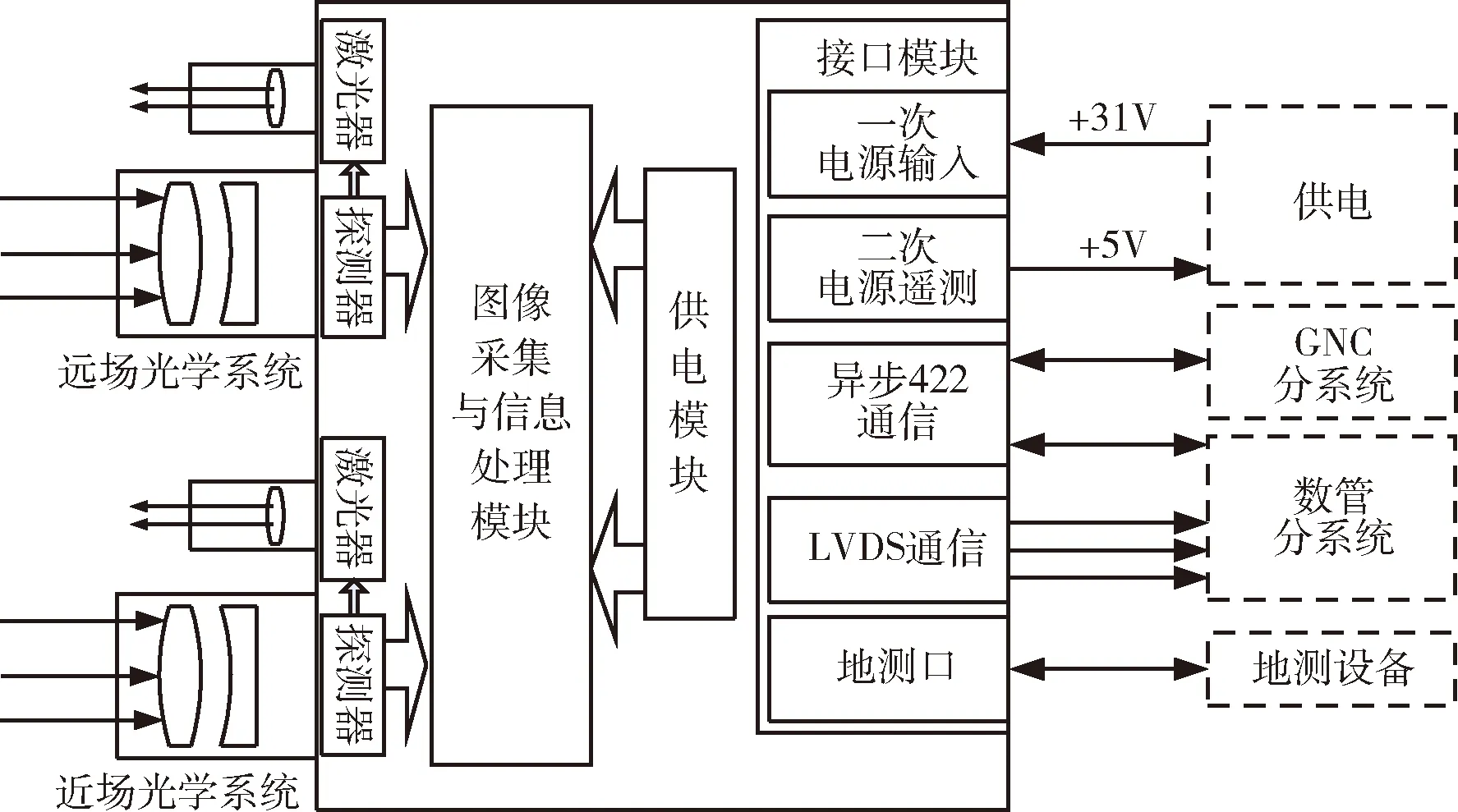
图2 TOF相机组成框架图Fig.2 Frame diagram of TOF camera

图3 TOF相机结构示意图Fig.3 Schematic diagram of TOF camera structure

1.3 TOF相机主要技术指标

本文根据空间非合作目标的目标特性分析相机的主要技术指标如表1所示，其中远场光学视场角为25°，近场光学视场角为75°，探测器分辨率为320 pixel×240 pixel以及调制频率为24 MHz、12 MHz、6 MHz、3 MHz、1.5 MHz、0.75 MHz可调，上述指标满足100-1.5 m非合作目标的探测需求.

表1 TOF相机主要技术指标Tab.1 Main technical index of TOF camera

2 数学模型

2.1 相机模型

TOF相机为小孔成像模型，针对空间中的三维点 成像过程如图4所示.根据小孔成像原理具有以下模型：

(2)

其中P=[xyz]T为三维点，p=[uv]T为在探测器像素平面投影点，K为相机内参，fx、fy为焦距，cx、cy为相机主点.

图4 TOF相机成像模型Fig.4 TOF camera imaging model

根据上述相机模型定义，相机内参K标定已知后，像素点对应的深度z通过探测器解析出来，即可利用小孔成像模型恢复目标点的三维空间坐标，具体恢复公式如下式.

(3)

TOF相机解析像素点对应的深度z的原理为利用调制激光的相位偏置进行解调，图5为解调原理图.

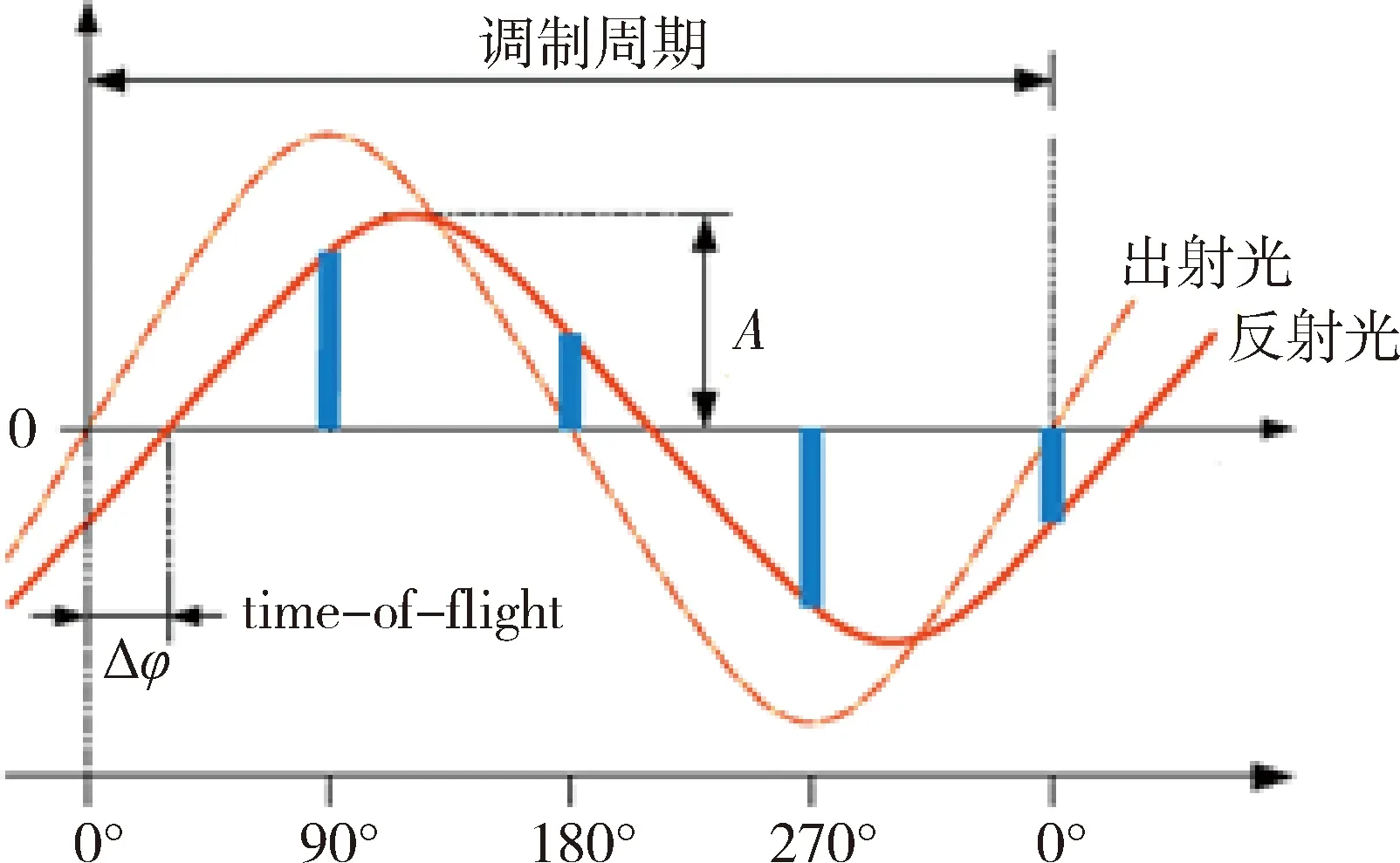
图5 TOF相机测距原理Fig.5 TOF camera ranging principle

假设出射光的正弦信号s(t)振幅为a，频率为ω，则出射光信号可表示为

s(t)=asin(ωt)

(4)

经目标表面反射后接收到的信号为r(t)，衰减后的振幅为A，时间延迟为Δt，对应相位延迟为Δφ，由环境引起的强度噪声为B，则反射光信号可表示为

r(t)=Asin(ω(t-Δt))+B=Asin(ωt-Δφ)+B

(5)

设置等间隔采样点，即保证相邻采样点间相位差为1/4调制周期，所选采样点为τ0=0°，τ1=90°，τ2=180°，τ3=270°.

4个采样点时刻信号如下：

(6)

根据式(6)计算相位偏移

(7)

利用式(1)计算物体深度信息.

计算接收信号振幅A，该信号反应目标的灰度信息.

(8)

2.2 坐标系定义和相对位姿定义

考虑追踪星和空间非合作目标两个目标，其中追踪星前端安装有TOF相机.由于TOF相机固定在追踪星上，追踪星的连体坐标系与TOF相机的连体坐标系相差一个已知且不变的变换矩阵，因此追踪星与非合作目标之间的相对位姿可以用TOF相机与非合作目标之间的相对位姿来表示.空间非合作目标运动状态不可知，但是当仅考虑追踪星与非合作目标之间的相对位姿，当以非合作目标为参考对象，仅追踪星在运动，因此不失一般性可以假设非合作目标不动，追踪星(即TOF相机)在运动.定义坐标系统以说明TOF相机和非合作目标之间的相对位姿，如图6所示.其中OS-xSySzS为TOF相机测量坐标系，坐标系原点OS位于相机光心，xS轴与yS轴分别与TOF相机图像坐标系的u轴和v轴相互平行；OT-xTyTzT为非合作目标对接环坐标系，该坐标系是根据TOF相机的灰度图像提取非合作目标的对接圆环，结合恢复的非合作目标的三维点云信息进行构建；OC-xCyCzC为非合作目标质心坐标，该坐标系不可知.

为了求解TOF相机与非合作目标之间的相对位姿，需要确定计算过程中的基准坐标系.由于非合作目标的质心坐标系OC-xCyCzC是不可知的，这导致无法将非合作目标的质心坐标系作为位姿估计过程中的基准坐标系.因此本文TOF相机求解可获得的非合作目标对接环坐标系OT-xTyTzT与TOF相机OS-xSySzS测量坐标系之间的相对位姿关系.如图6所示，TOF相机与非合作目标之间的相对位姿用Hi表示，该位姿量由6个位姿参数定义，包括3个旋转分量和3个平移分量，Hi表达式为

(9)

其中，0为一个元素均为0的3维向量，旋转矩阵Ri和平移矩阵Ti的表达式分别为

(10)

(11)

其中，αi、βi、γi分别表示依次绕OC-xCyCzC的X轴、Y轴、Z轴旋转的滚转角、俯仰角、偏航角，Δxi、Δyi、Δzi分别表示沿OC-xCyCzC的X轴、Y轴、Z轴的3个平移分量.

图6示意了TOF相机位姿变换量R1i，T1i，该旋转与平移矩阵表示TOF相机自身的运动量，该量可以通过H1与Hi表示

(12)

H1i=H1(Hi)T

(13)

追踪星对空间非合作目标进行逼近过程，需要TOF相机提供非合作目标对接环坐标系OT-xTyTzT与TOF相机OS-xSySzS测量坐标系之间的相对位姿关系，因此本文需求解Hi该相对位姿量.

图6 坐标系定义Fig.6 Coordinate system definition

3 位姿估计算法框架

非合作目标的位姿估计算法框架主要包括两个步骤：位姿初始化和跟踪，如图7所示.其中位姿初始化主要是通过获取的灰度图像和三维点云数据通过几何特征的提取、PCA主成分解算或者基于模型采样的模板匹配获取当前位置的初始位姿，然后利用基于点云的ICP迭代优化算法进行相对位姿优化；跟踪过程则是当初始化过程获取的相对位姿满足一定条件(前后角度变化小于某个阈值或平移量小于某个阈值等判别条件)时进入跟踪模式，该模式下主要利用前序位姿以及运动模型预测当前的相对位姿，最终仍利用基于点云的ICP迭代优化算法进行位姿优化[7-15].

本文利用TOF相机进行非合作目标的相对位姿解算，TOF相机可以同时获取非合作目标灰度图像和深度图像，因此采用基于灰度图提取目标几何特征的初始化方案，位姿优化使用ICP迭代算法，跟踪采用卡尔曼滤波模型估计，整体算法框架如图8所示，后续分别将上述模块进行阐述.

3.1 基于弧段的椭圆提取

椭圆为空间目标常见的几何特征，利用算法检测空间目标中的椭圆信息进行解算位姿在相对位姿解算有着比较广泛的应用.传统椭圆检测算法主要分为两类：第一类是基于边缘点的椭圆检测算法，该类算法主要是利用图像中的边缘点通过RANSAC或者随机椭圆算法进行椭圆监测拟合；第二类是基于弧段的椭圆监测算法，该类算法是聚合边缘点为弧段，然后利用弧段满足同一椭圆的约束条件将同一个椭圆的弧段筛选出来完成椭圆监测[16].本文采用基于弧段的椭圆提取算法，具体算法流程如下.算法效果如图9所示，其中红色椭圆为提取获得椭圆.

图7 位姿估计算法流程图Fig.7 Flow chart of pose estimation algorithm

图8 位姿估计算法框架图Fig.8 Frame diagram of pose estimation algorithm

表2 算法1流程Tab.2 Algorithm 1 process

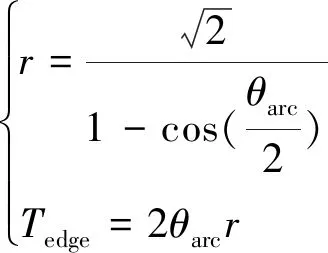
(14)

其中，θarc为弧段的弧长，r为对应弧段的半径长度，Tedge表示边缘弧段长度.

Ax2+Bxy+Cy2+Dx+Ey+F=0

(15)

其中，A、B、C、D、E、F为椭圆方程6个参数，x、y表示椭圆上的坐标点.

图9 椭圆提取示意图Fig.9 Schematic diagram of ellipse extraction

3.2 基于点云数据的ICP算法

针对刚性物体的运用采用点云配准算法进行相对位姿求解，ICP算法最早与1992年已经被提出用于解决相对位姿求解问题[12].该算法主要解决点集之间的匹配与位姿求解，如图10所示为算法示意图，其中蓝色点集为运动参考点，红色点集为待配准点，通过算法获取两者之间的相对位姿.

图10 点云配准示意图Fig.10 Point cloud registration diagram

具体算法主要分为4步：

1)搜索最近点；

2)通过配准点对进行SVD(singular value decomposition)分解；

3)计算姿态变换矩阵Rk,k-1、平移矢量tk,k-1；

4)求解误差，通过阈值判断是否继续迭代.

3.3 位姿跟踪

跟踪利用经典Kalman滤波算法建立参数方程，将角度信息作为系统状态输入.具体为将本帧的角度信息作为观测信息，与利用前一帧的信息计算出来的预估状态进行对比，求解出误差项，重复此过程，对参数方程进行递推，不断求解参数并进行更新，使预估状态与观测状态的趋于一致.当目标跟踪失效时，无法得到观测信息，将Kalman算法求解得到的预估状态作为TOF相机与目标之间的角度信息，使系统在恢复后依旧能正常跟踪目标.

假加速度为常数的运动模型，根据加速度模型，卡尔曼滤波模型中状态方程和观测方程分别为

xk=Φxk-1+Gwk-1

(16)

zk=Hxk+vk

(17)

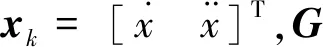
Kalman滤波算法为

(18)

(19)

(20)

(21)

(22)

4 实 验

4.1 地面实验

根据上述算法框架设计，利用TOF相机进行试验验证，试验现场示意图如下所示，利用双机械臂分别模拟追踪星与空间非合作目标，图中红色为TOF相机，具体试验流程为：右机械臂模拟空间非合作目标进行章动，左机械臂模拟追踪星利用TOF相机进行三轴位姿解算，将相对位姿输出给GNC/模拟数管，加入GNC导航控制算法获取机械臂控制量，驱动左机械臂向前逼近.

图11 地面验证试验示意图Fig.11 Schematic diagram of ground verification test

如图12为试验中目标成像效果图，图13(a)为逼近过程中三轴相对位置数据，图13(b)为逼近过程中三轴相对姿态角数据.由数据可知整个过程数据稳定可靠，TOF相机姿态精度优于2°，位置精度优于5 cm.

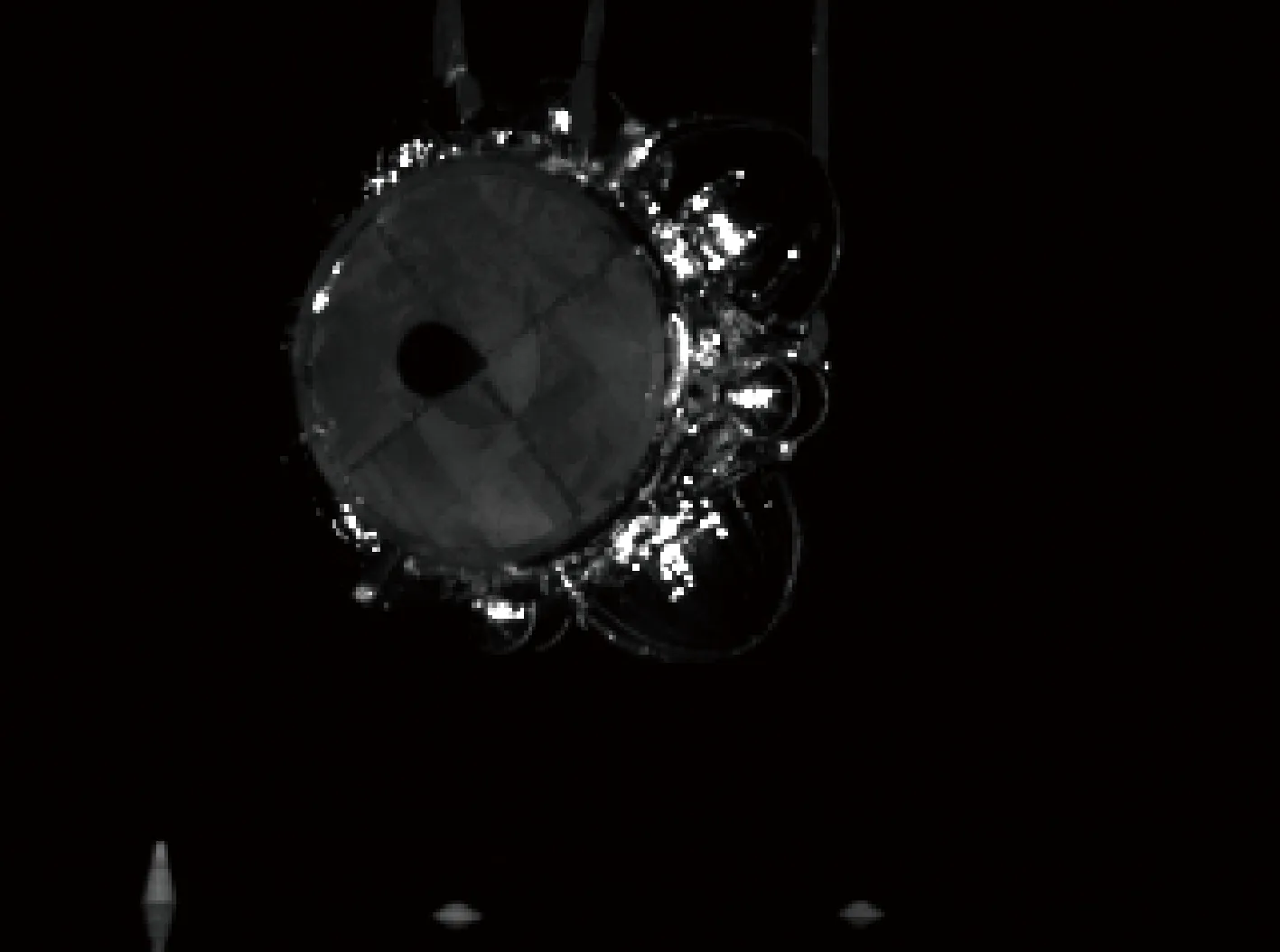
图12 TOF相机目标成像示意图Fig.12 Schematic diagram of TOF camera target imaging

图13 TOF相机输出三轴位姿曲线Fig.13 TOF camera output three-axis pose curves

4.2 在轨试验

TOF相机配套某卫星型号进行在轨服务任务验证试验，作为超近程逼近主份测量单机进行应用，在轨逼近过程在轨数据如图14所示，整个过程数据稳定可靠且与地面测试精度相当，保障了任务圆满完成.

图14 TOF相机输出三轴位姿曲线(在轨)Fig.14 TOF camera output three-axis pose curves (in orbit)

5 结 论

本文利用TOF新体制主动光成像相机对非合作目标进行探测，同时获取非合作目标的灰度与三维点云信息，提出融合非合作目标的二维灰度与三维点云数据的相对位姿估计算法框架，该算法框架弥补了灰度图像缺乏距离信息和三维点云数据缺乏目标纹理特征的不足，最后结合卡尔曼滤波的跟踪模型，解决了空间一类诸如星箭对接环具有圆几何特征的非合作目标相对位姿估计的问题.地面与在轨试验表明TOF相机位姿估计稳定可靠，相对位姿精度优于2°、5cm，因此本文所提方案可行，可为后续针对空间非合作目标的相对位姿估计需求提供工程设计参考.