航天器多约束空间抵近掠飞轨迹优化方法

张庆泽， 尹龙逊， 张 强， 王 博， 叶 东*， 王佐伟

1. 哈尔滨工业大学,哈尔滨 150001 2. 北京空间飞行器总体设计部,北京 100094 3. 北京控制工程研究所,北京 100094

0 引 言

由于航天器在通信、数据中继、预警等方面的应用,其军事价值也越来越为世界各国所重视，空间攻防对抗已成为太空领域的热点问题，这其中就包括对敌方的目标航天器实施侦查、破坏其部件结构，干扰航天器的正常运行等任务，这些任务均以破坏目标航天器相关功能、扰乱对方部署为战略目的.受观测距离和地面测站分布的限制，现有地基空间监视系统很难实现对目标航天器进行全域、精细的观测.为此，利用观测航天器近距离接近目标航天器，实现对航天器的抵近观测就成为空间态势感知技术发展的一个重要方向.由于航天器本身携带的燃料极为有限，很难通过机动完全规避目标，同时也会影响到自身的正常工作，如何对己方航天器进行合理的轨道规划，从而使得在实现燃料最省的同时满足任务需求就成为了重点关注的问题.

针对轨道优化，许多学者提出了相关算法.刘恒等[1]建立了脉冲轨道机动参数优化模型，确定了燃料最省的最优脉冲次数.杨俊[2]采用改进的遗传算法，得到了共面、异面下的多脉冲交会轨道燃料最优解.李玉玲[3]提出了一种基于自适应遗传算法的多星协同攻击轨道规划方法，规划了多星协同下燃料最优的轨道设计.蒯政中[4]采用序列二次规划间接法，基于脉冲和电推进，针对特定轨道航天器位置保持和转移策略进行了研究.任仙海等[5]运用了优化算法针对序列访问进行了研究.梁记源[7]考虑单一成像问题，利用启发式算法对多目标进行了访问序列规划.肖余之等[8]利用三维重建技术，形成了基于轨道机动平台的高轨目标精准感知技术，可对来袭目标进行跟踪监视.曲耀斌等[9]考虑光照约束的地球同步轨道航天器自主绕飞，设计了一种GEO轨道附近的绕飞策略.

陈阳等[10]对高轨道航天器进行可见性建模，进行了多约束下的隐秘轨道转移仿真分析.为了得到在现有燃料条件下航天器在空间中的可达范围，于瀚[11]通过矢量推导得到了一定燃料下航天器的可飞行区域.崔红正等[12]针对非合作空间目标轨道机动检测问题，提出普适性轨道机动检测策略，研究了不同推力条件下的轨道机动能力.盛靖[13]利用遗传算法，建立了小椭圆条件下的应急轨道模型，提高了航天器快速机动能力.LUO等[14]提出了加速机动转移轨道策略问题，并对其进行了仿真验证.

李九天[15]研究了多目标小行星访问问题，采用高斯伪谱法进行全局优化，得到了价位理想的结果.CAO等[16]考虑轨道及姿态特性，优化了电推力下的轨道转移机动策略.刘胜男[17]结合进攻收益、进攻成本、燃料消耗、目标覆盖度、毁伤度等建立了综合效能函数，基于Nash均衡理论，建立了针对多目标航天器的进攻路径分配.

上述参考文献大多侧重于轨道优化策略的研究，而任务背景性或优化目的性不强.本文提出了一种基于序列二次规划算法和多步优化相结合的方法，将近程观测任务转化为非线性约束问题，并采取适合的模型将非线性约束简化，从而得到燃料最优解.该方法具有计算效率高、鲁棒性强、收敛快的特点，适合多种抵近观测任务的规划.

1 问题描述与规划

1.1 任务描述

航天器抵近观测有多种方式，本文研究的问题主要针对掠飞观测任务.掠飞观测是指任务航天器沿轨道从目标附近自由掠过时，根据航天器与目标之间的相对位置关系，控制其姿态使观测轴始终指向目标进行连续观测的过程，如图1所示.

图1 掠飞观测示意图Fig.1 Flyby observation

整个任务过程分为远程和近程两个阶段，任务航天器通过远程机动段机动至目标航天器附近的停泊点处，停泊一段时间后进行近程机动至目标附近进行观测任务，同时需满足观测时段的约束条件.在近程段，为具有对目标成像的能力，还需满足成像距离、成像光照角、姿态机动角速度、姿态机动角加速度等要求.

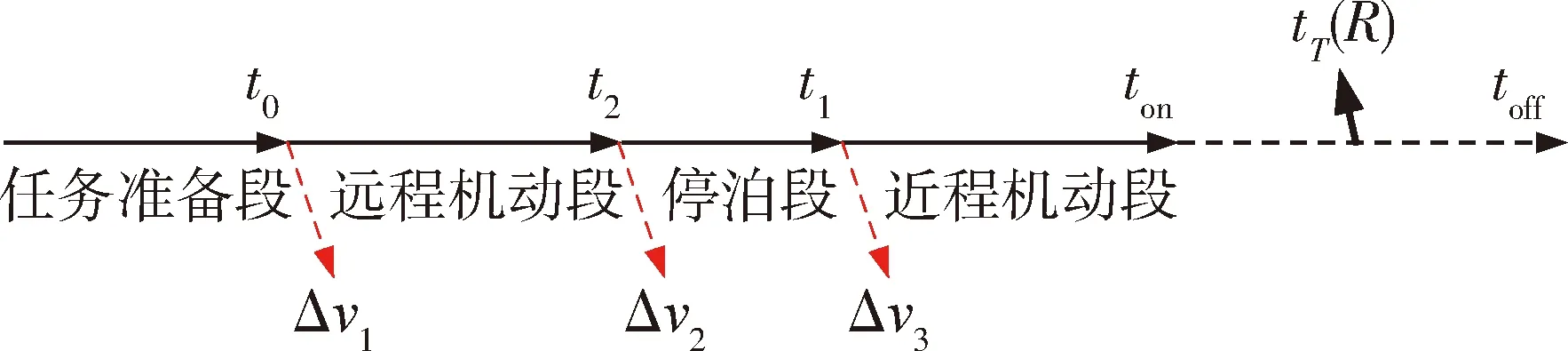
图2 任务时段Fig.2 Task time intervals

事件轴如图2所示，任务航天器经过起始准备段和远程机动段到达目标附近的停泊点，停泊一段时间后近程机动至目标附近，于任务要求时刻进行成像观测任务，观测时段为ton至toff，tT为观测时段时间中点，R为该时刻观测距离，以上过程形成如下优化问题：

优化变量X=(t0,t1,t2,R)，目标函数J=|Δv1|+|Δv2|+|Δv3|.

整个任务过程理论上存在无数个能够完成任务的可行解，因此选取合适的优化解，找到满足观测时段约束条件同时使得整个任务燃料消耗最少的轨道即为优化目的.

1.2 任务规划

任务航天器需要对目标航天器实施抵近侦察成像的任务.为此，整个过程需要得到目标执行任务的大概时间，以获得任务星的机动窗口，从而确定整个任务时间.将近程段的成像光照条件、姿态机动能力、观测距离等任务需求，根据所用的近程相对运动简化模型，转化为近程优化所需满足的约束.以燃料最优为优化指标，采取多步优化得到最终的结果，输出相关数据，验证方法的有效性和正确性.

整个优化过程采用序列二次规划(SQP)算法[6]，该算法具有计算精度高、收敛速度快、稳定性好等优点，在求解含有等式约束和不等式约束的非线性规划问题都具有很好的收敛性.

2 约束模型及其简化处理方法

通常而言，近程段初始时刻目标航天器在轨运行，观测航天器从目标航天器附近的停泊点处开始机动，抵近目标航天器.在合适的时段内观测相机开机并对任务目标执行近距离的观测任务.在观测时段内航天器需满足约束条件，几种基本约束如下：

1)太阳光约束：若使观测航天器具有对目标观测及成像的能力，两星相对位置需满足良好的成像光照角度.

2)姿态角速度约束：在近距离观测的过程中，观测航天器自身的姿态机动能力具有最大姿态角速度的限制.

3)观测距离约束：航天器的成像相机具有最大观测距离，近距离观测过程中两星距离不能超过该值.

4)安全距离约束：通常任务星与目标星的距离不能过于靠近，观测航天器需始终位于目标的安全距离以外.

上述提到的约束直接用于优化处理容易造成计算量大、优化器处理时间长、算法不易收敛等缺陷，因此需要将模型进行简化便于算法处理相关优化问题.

约束处理的基本思想为：以任务航天器的机动时间为优化变量，燃料消耗为优化指标，基本约束通过模型简化的方式处理为非线性约束，将掠飞观测任务转化为一个优化问题.

(1)使任务航天器(记为A星)于tT时Lambert机动至目标航天器(记为B星)与太阳连线方向，观测距离为R，机动起始时刻A星的速度增量可解，A星的机动轨迹便可求取.D、E分别为观测航天器成像相机的开机点与关机点，tT为二者的时间中点，设A'为观测时段(DE弧段)内具有最大成像光照角的空间位置(图3中假设为E点)，则太阳光约束要求：

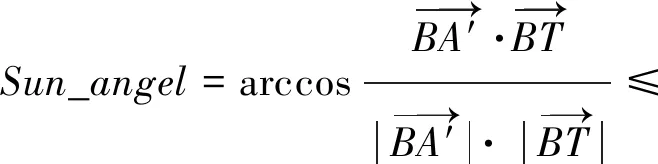
(2)A星观测时段内需满足姿态角速度约束，要求：

其中delta_t=t_off-t_on，为A星实际掠飞观测窗口时长.

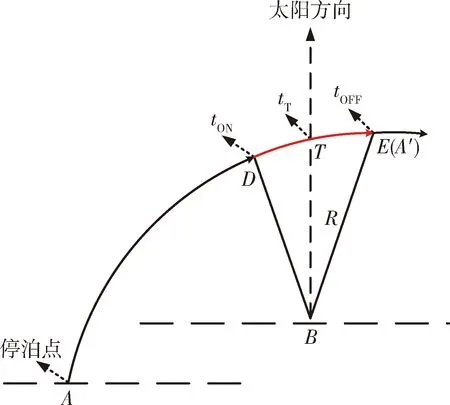
图3 约束处理示意图Fig.3 Constraint processing diagram

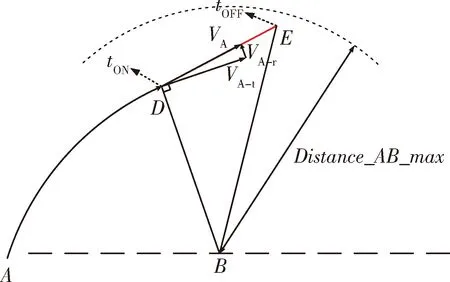
图4 观测距离约束简化模型Fig.4 Simplified model with observation distance constraint

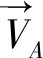
图5 安全距离约束简化模型Fig.5 Simplified model of safe distance constraint

对于上述约束的模型简化处理在仿真结果分析中可以看出，该模型相对于真实轨道模型更加保守，因而可以更加满足约束从而完成任务.

3 高效多步优化策略

上节描述的简化模型可作为非线性约束进行添加，从而将任务转化为非线性规划问题.非线性规划问题是目标函数或约束条件中包含非线性函数的规划问题.通常，解非线性规划要比解线性规划问题困难得多.并且，不同于线性规划有单纯形法这一通用方法，非线性规划目前还没有适于各种问题的一般算法，各个方法都有自己特定的适用范围.

本文选取序列二次规划算法(SQP)进行优化求解.序列二次规划的基本思想即是利用泰勒展开将非线性优化问题的目标函数在迭代点处简化为二次函数，同时将约束函数简化为线性函数.

非线性约束最优化问题可以描述为

minf(x)
s.t.gu(X)≤0(u=1,2,…,p)
hv(X)=0(v=1,2,…,m)

利用泰勒展开把非线性约束问题的目标函数在迭代点Xk简化成二次函数，把约束函数简化成线性函数后得到的就是二次规划问题.

与遗传算法等传统算法相比，SQP算法在使用过程中无需频繁调整某些因数使得算法更快速得到某一结果，具有广泛适用性，同时它的收敛性好、计算效率高、边界搜索能力强，符合星上解算实时求解、实时规划的要求.

但SQP方法也存在对初值有一定的敏感性，某些情况下易陷入局部最优的问题.因此为了避开这些缺陷，本文设计了一种多步优化的策略，将上一步的结果作为下一步优化初值的参考值或边界进行优化，避免陷入局部最优的同时加强了算法搜索能力.

针对任务需求存在停泊的优化流程图如图6示，包括以下步骤：

1)首先输入执行任务相关初始条件，确定任务时间，即航天器A的默认抵近观测时间.

2)在输入完成后，首先进行的是近程优化.由于远程段的机动变轨消耗燃料远多于近程段燃料消耗，而一般远程时间越长燃料也就越省因此第一次优化近程段在满足任务需求的前提下以时间为优化变量，通过算法找到满足近程约束的最短执行任务时间，以该时间作为下一步远程优化的上界，使得远程变量选取的范围得到确定.

3)得到从初步近程优化的时间上界后，远程优化变量范围确定，该阶段包括两个时间变量t0、t1，前者是A星自由飞行时间，后者是机动后的自由飞行时间.远程优化的目的在于远程段燃料最优，这一步骤得到的t1将作为第二次近程优化的下界.

4)得到远程规划确定的时间下界后，对近程进行第二次优化，与第一次优化目标是时间最短相比，第二次近程优化的目标是燃料最省，优化后得到满足任务需求下的燃料最省的近程机动时间.

5)将远程和近程二次优化得到的时间变量 放入全局优化中进行最终优化，得到满足任务需求下的燃料最省的全部机动时间和所消耗的燃料.

具体流程图见图6.

图6 轨迹优化流程示意图Fig.6 Schematic of trajectory optimization process

4 数值仿真及分析

本节中，任务航天器针对特定轨道上的目标进行掠飞观测任务，要求24 h后执行观测任务，观测时长1 h，停泊点处至少停泊1 h.通过两种不同场景的仿真实例(工况条件和约束指标不同)，对所设计的多步优化策略进行仿真验证.

场景1：A星(任务航天器)对B星(目标航天器)执行掠飞观测任务，远程机动至停泊点，停泊点停泊等待后近距离机动至B星附近，于规定时刻进行观测成像任务，A星成像过程中需满足四种基本约束.该问题的优化变量X=(t0,t1,t2,R)，优化指标J=|Δv1|+|Δv2|+|Δv3|，即任务全程燃料最优.场景1观测时段内任务航天器约束指标如表1所示；表2为两星初始轨道根数，任务停泊点位于B星轨道前方30 km共轨处(相位差+0.04°)：

表1 场景1任务约束Tab.1 Task constraints of scenario 1

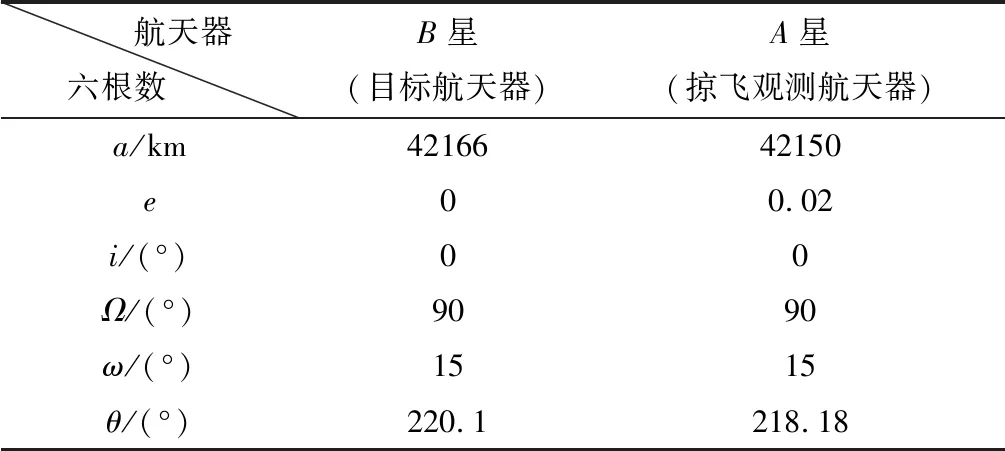
表2 场景1轨道初始参数Tab.2 Initial orbit parameters of scenario 1

利用本文提出的多步优化策略进行求解(③)，与按未优化的可行解(①)、直接优化(未采用多步优化)(②)的结果进行对比，仿真结果见表3.

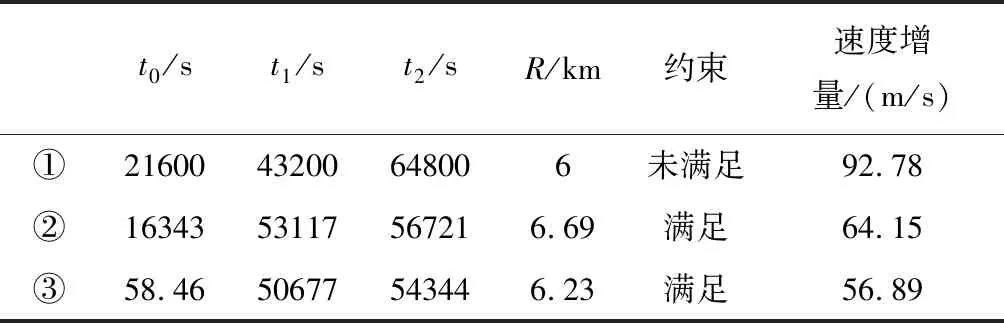
表3 场景1优化结果对比Tab.3 Comparison of optimization results of scenario 1

根据多步优化仿真结果，得到任务各指标在观测时段内的变化曲线如图7-9所示，均满足观测时段内的约束指标.

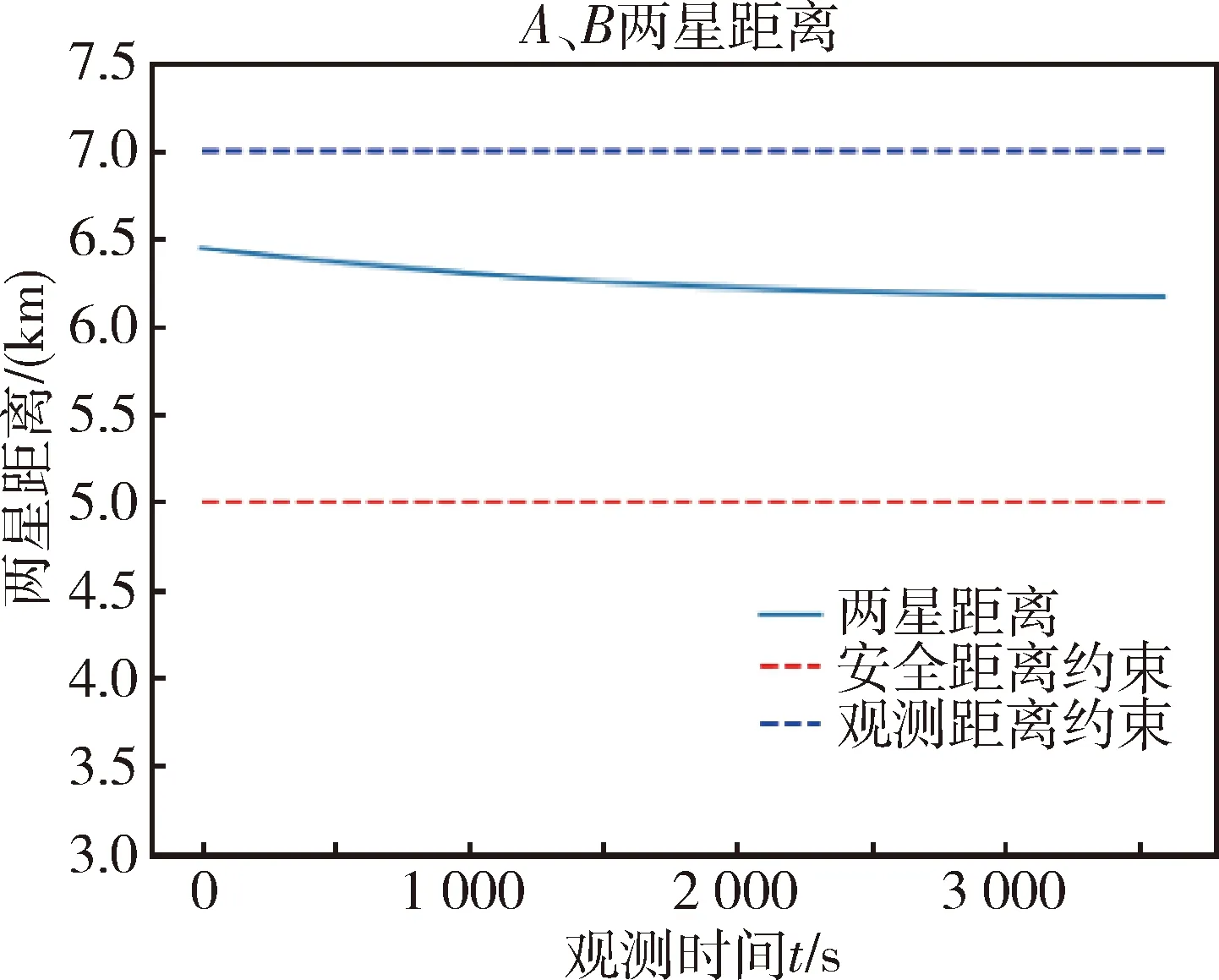
图7 两星距离变化曲线Fig.7 Changes of the distance between two satellites

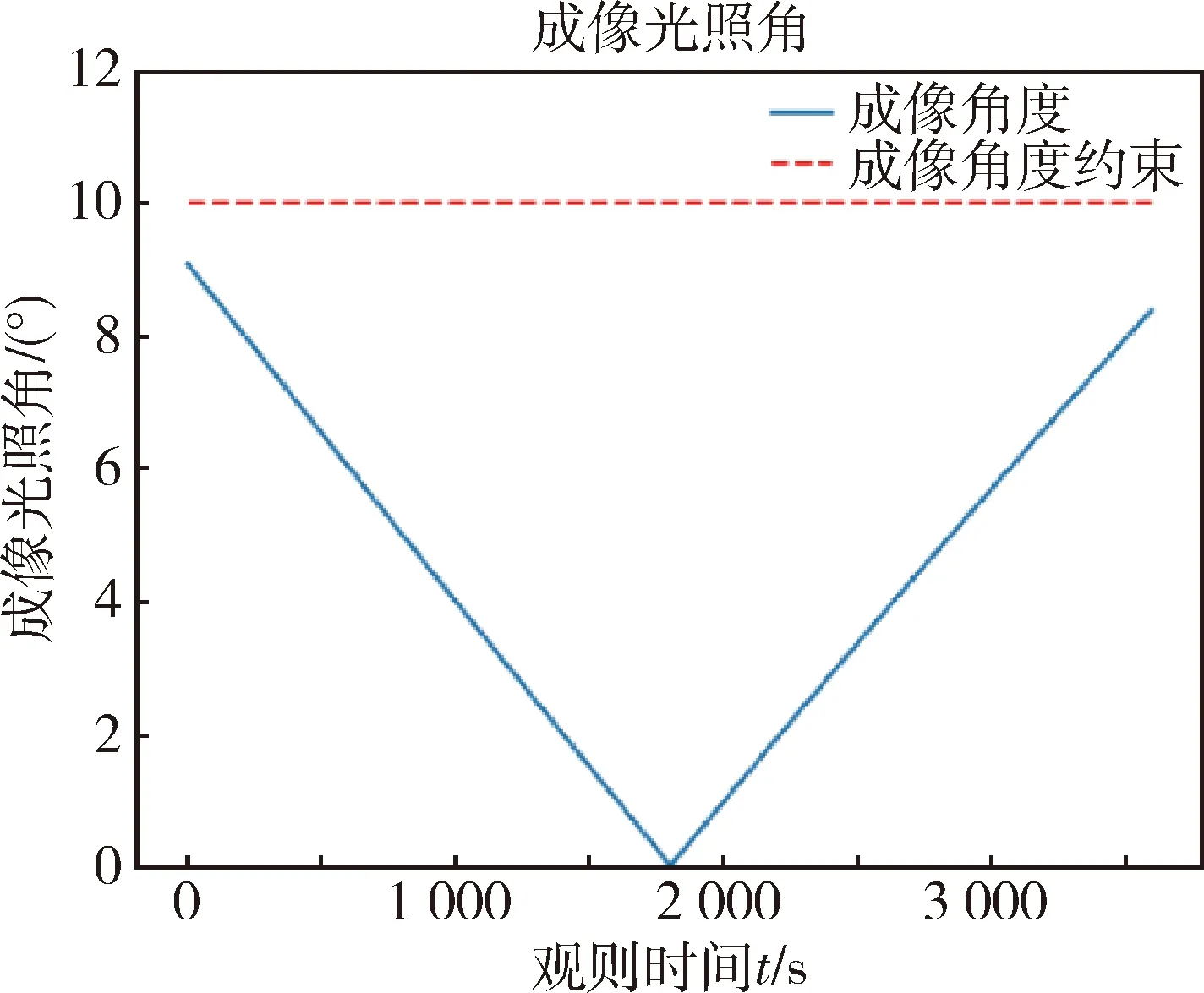
图8 成像光照角变化曲线Fig.8 Changes of imaging light angle

图9 A星姿态角速度变化曲线Fig.9 Changes of satellite A attitude angular velocity

场景2：场景2观测时段内任务航天器约束指标如表4所示；两星初始轨道根数如表5，任务停泊点位于B星轨道后方100 km共轨处(相位差-0.14°)：

表4 场景2任务约束Tab.4 Task constraints of scenario 2

表5 场景2轨道初始参数Tab.5 Initial orbit parameters of scenario 2

通过本文提出的多步优化策略进行求解(③)，与按未优化的可行解(①)、直接优化(未采用多步优化)(②)结果进行对比，结果见表6.

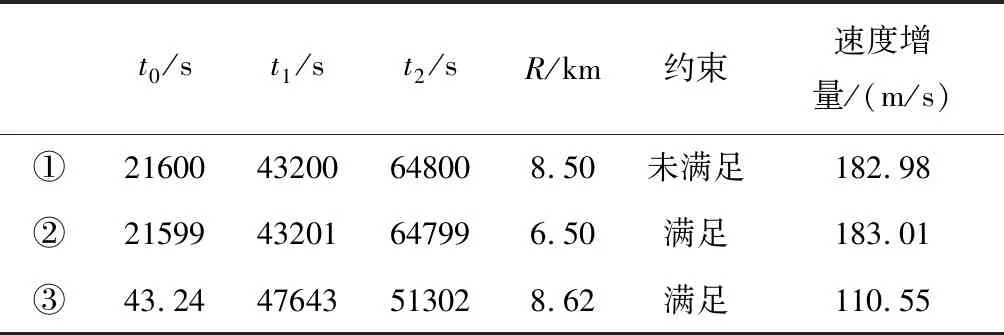
表6 场景2 优化结果对比Tab.6 Comparison of optimization results of scenario 2

根据多步优化仿真结果，得到任务各指标在观测时段内的变化曲线如图10-12所示，均满足观测时段内的约束指标.

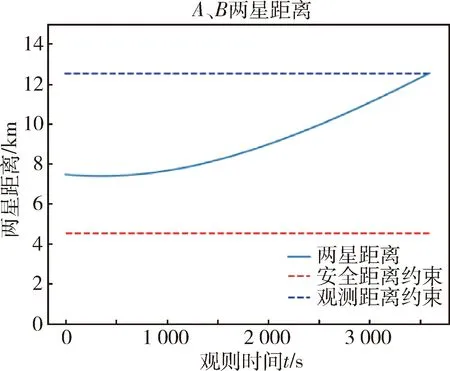
图10 两星距离变化曲线(实例2)Fig.10 Changes of the distance between two satellites (example 2)

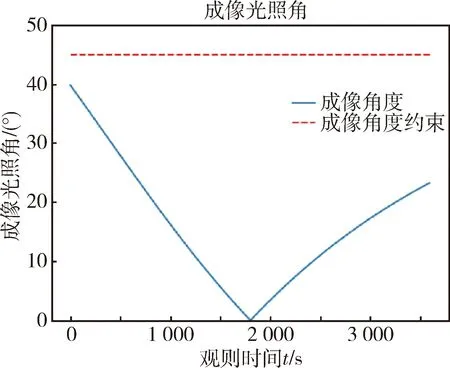
图11成像光照角变化曲线(实例2)Fig.11 Changes of imaging light angle (example 2)

多步优化流程：以场景2为例，按多步优化方法求解的具体流程见图13.

以上两个仿真实例，通过将本文所设计的多步优化策略所得的优化解，与任一可行解、直接优化解(未采用多步优化)进行对比，可知任一解由于未采用优化，约束和燃料消耗情况均不能到达理想效果；在实例一中，直接优化解与任一解相比，燃料消耗已明显减少，但未达到最优，且稳定性不高(实例二中未能成功优化)，而多步优化策略均能成功收敛到最优解，且满足掠飞观测任务所需的约束条件.当然，代价是计算量及优化时间略有增加.

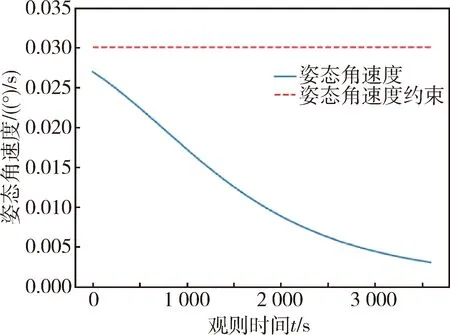
图12 A星姿态角速度变化曲线(实例2)Fig.12 Changes of satellite A′s attitude angular velocity(example 2)

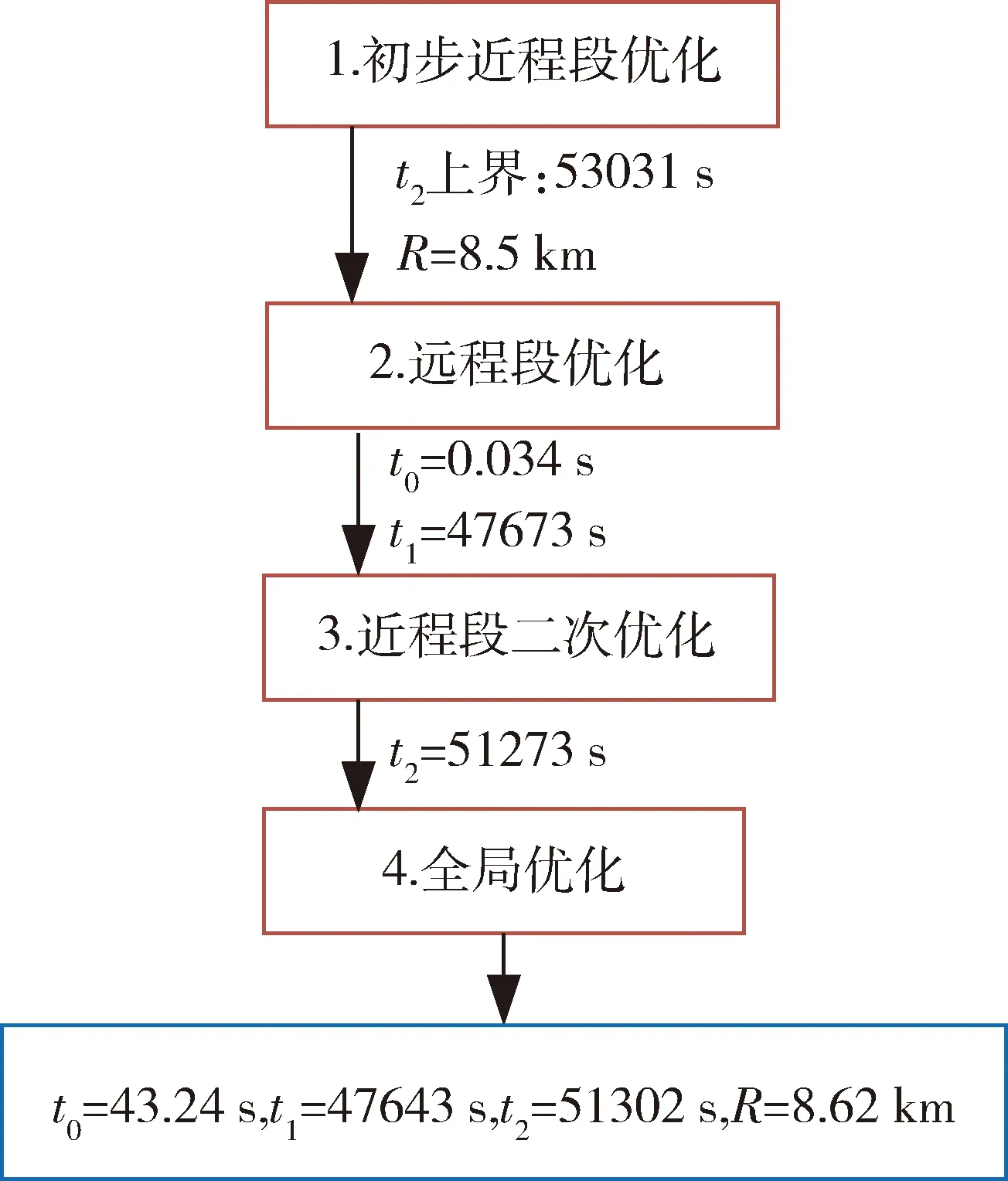
图13 多步优化流程(场景2)Fig.13 Multi-step optimization process (scenario 2)

5 结 论

针对目标航天器采取的掠飞观测任务，本论文采用多步优化与序列二次规划相结合的方法，将所要执行的任务转化为具有非线性约束的优化问题，同时设计了一种多步优化策略，与任一解和直接优化结果相比，该策略具有较高的精确度，便于快速收敛到最优解，同时仿真结果证明算法具有较强稳定性，得到了在任务规定时间内满足任务需求且燃料消耗最优的转移轨道.

由于该方法具有较高的计算效率和收敛性，因此适用于多种不同策略的抵近观测任务，可保证在轨应用所必须的实时性和鲁棒性.