空间机动飞行器末级火控机构目标控制量修正方法

宁 宇， 王露莎， 邓家权， 宫经刚， 王明明

1. 北京控制工程研究所,北京100094 2. 航天器在轨故障诊断与维修重点实验室,西安 710043 3. 63798部队,西昌 615606 4. 西北工业大学,西安 710072 5. 航天飞行动力学技术重点实验室,西安 710072

0 引 言

随着太空军事化发展，控制太空已成为未来战场的“战略新高地”,以太空为背景的多域融合作战已成为大国间战争的重要形态.自2001年以来，美军已进行了十余次“施里弗”演习[1-2]，大国间的太空对抗已逐渐显性化和常态化.美国空军提出“全球警戒、全球到达、全球作战”的战略思想，确定了要构建“全球到达、全球存在、全球感知”的太空空间侦察监视体系，以满足太空威胁实时响应需求.在GEO轨道上运行着大量高价值航天器，美国早在2006年，已经开始在高轨部署了，包括MiTEx、GSSAP、ANGELS、EAGLE、Mycroft、S5等型号[3-4]在内的，能够用于实战的攻防航天器，对我国高轨高价值航天器的威胁尤为严重.

为保障良好的空间安全，各国积极研制主动和被动空间安全系统[5-6]，一般包括软载荷和硬载荷，如动能、激光、网电等载荷[7].在轨安全载荷安装在主动航天器平台上，对目标跟瞄时，两个航天器一般处于轨道面交会点位，航天器间相对运动切向速度和视线角速度都达到峰值，并且航天器尺寸相比于相对距离，一般相差2-4个数量级，同时主动航天器处于空间失重状态，平台没有外部稳定支撑.上述条件大幅提升了主动航天器载荷持续命中目标航天器的难度，由此对空间安全平台在轨火控技术提出了高精度指向要求.

空间载荷一般安装在一级或二级平台上，载荷输出端配置末级控制机构.由多级平台联合[8]完成对空间目标指向精确测量和控制，并将实时测量结果向末级控制机构反馈.该结果是末级控制机构的控制量输入来源之一，其精度对脱靶情况有直接影响.采用常规算法对指向矢量进行控制，一般过程是通过测量所得指向矢量，将载荷旋转至期望方向.该过程中存在随机误差，其二阶项通常被忽略，这是由线性化矢量观测模型导致的.当控制量输入值与随机误差比值在一定范围内时，若继续忽略该项，则会产生几何观测与代数计算不匹配现象，对指向精度影响显著.对测量所得指向矢量的描述若采用加法观测模型[9]，则实际矢量与误差矢量相加后获得在使用的测量矢量，一般认为误差矢量与实际矢量正交，这就导致测量矢量失去单位性.MARKLEY[10]研究了该项超出单位化约束的误差项，认为由于先进视线矢量测量元件具有极高精度[11]，导致该误差项在误差协方差矩阵中作为小量可以忽略.MORTARI[12]提出了能够反映真实旋转的非线性乘法观测模型，包含了二阶项，保证了观测的单位性，经分析认为二阶误差项在特定情况下仍然对估计具有较大影响[13]，并将该模型应用于对相对导航中位置估计[14].

本文通过分析现有单位矢量观测误差对空间平台末级火控机构指向的影响，利用乘法观测原理获得了对指向误差的修正方程，对修正方程有效性进行了检验，由简化运动模型进行数值计算，获得有效修正区域，并对空间平台控制状态下采用修正方法对载荷指向进行修正算数值仿真，验证了修正方法的有效性.

1 修正方法理论基础

平台姿态测量误差会传递至当前载荷指向控制中，该误差在数学上，由单位矢量的观测方程描述.通过加法观测模型和乘法观测模型比较，提出对末级火控机构控制量(指末级转动控制输入)修正方法的理论基础.

1.1 加法观测模型

对单位矢量观测的描述通常采用加法观测模型[9]，即观测量等于真实矢量与误差矢量之和，误差矢量服从高斯分布.

bi=Cri+vi

(1)

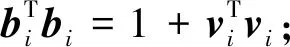
(2)

其中，σi为噪声标准差，I为单位阵.bi在Cri正交面上投影为

(3)

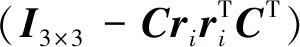
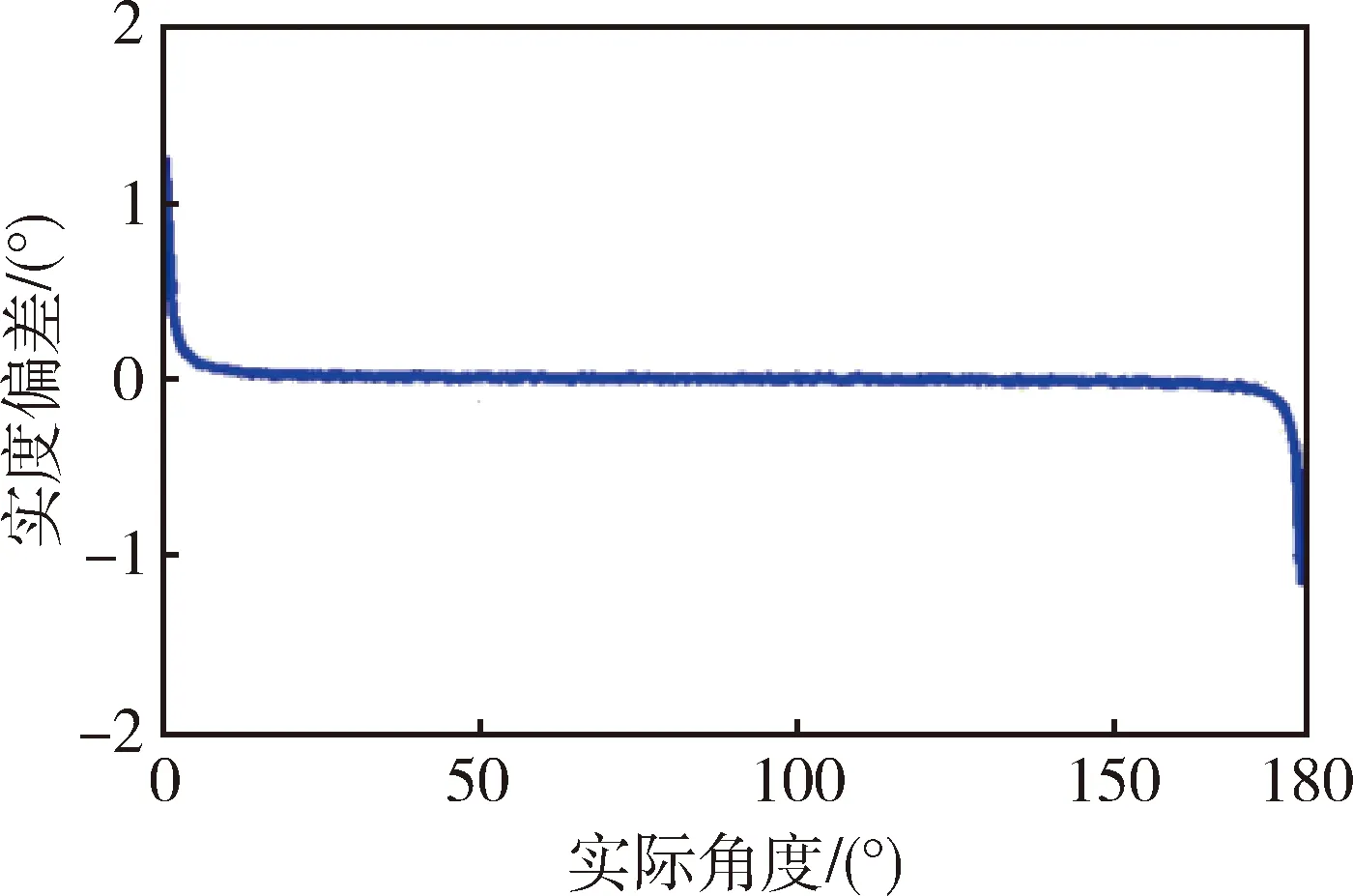
图1 加法观测模型误差Fig.1 Additive measurement model error

图1给出了加法观测模型的角度误差，即30000次误差均方差为1°的rj观测量与ri的夹角均值和加法观测模型期望值之间的差值.当两个矢量接近时，加法观测模型误差较大.

1.2 乘法观测模型

乘法观测模型[12]通过矢量旋转描述观测矢量，观测量等于真实矢量与噪声矩阵乘积，即

bi=Roti(mi,φi)Cri

(4)

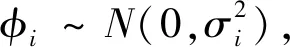
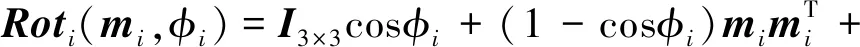
(5)

bi=Roti(mi,φi)Cri=Cricosφi+nisinφi

(6)

由于

(7)

故

(8)

非线性的乘法观测模型保证了观测矢量的归一化和噪声的正交性，比加法观测模型更准确地反映了实际观测.从数学意义上而言，角度不能服从高斯分布，因为角度变化范围有限.但是由于单位矢量观测敏感器一般具有较高精度[11]，角度在[0,π/2]内的变化时可以近似认为其服从半边的高斯分布.

1.3 测量矢量内积计算

(9)

其中

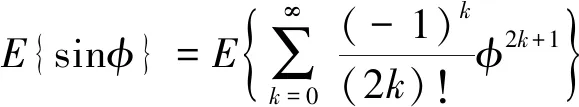
(10)

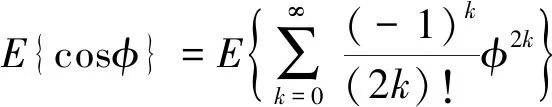
(11)

根据文献[15]，有

(12)

将式(12)代入式(11)，有

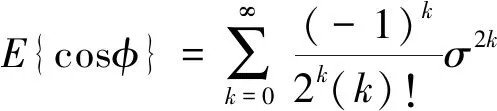
(13)

1.4 矢量内积偏差几何原理

采用加法观测模型计算两个观测矢量内积是无偏的，而乘法观测模型所得式(13)表明内积是有偏的.两个单位矢量观测值之间夹角余弦值期望小于真实矢量余弦值，故观测量间夹角期望会大于真实矢量夹角.如图2所示，若bi数量充足，分布在Cri周围圆锥中，被绕Crj的圆锥切割为两部分，其中A区内观测矢量数目统计上多于B区，故观测夹角均值应大于真实夹角.

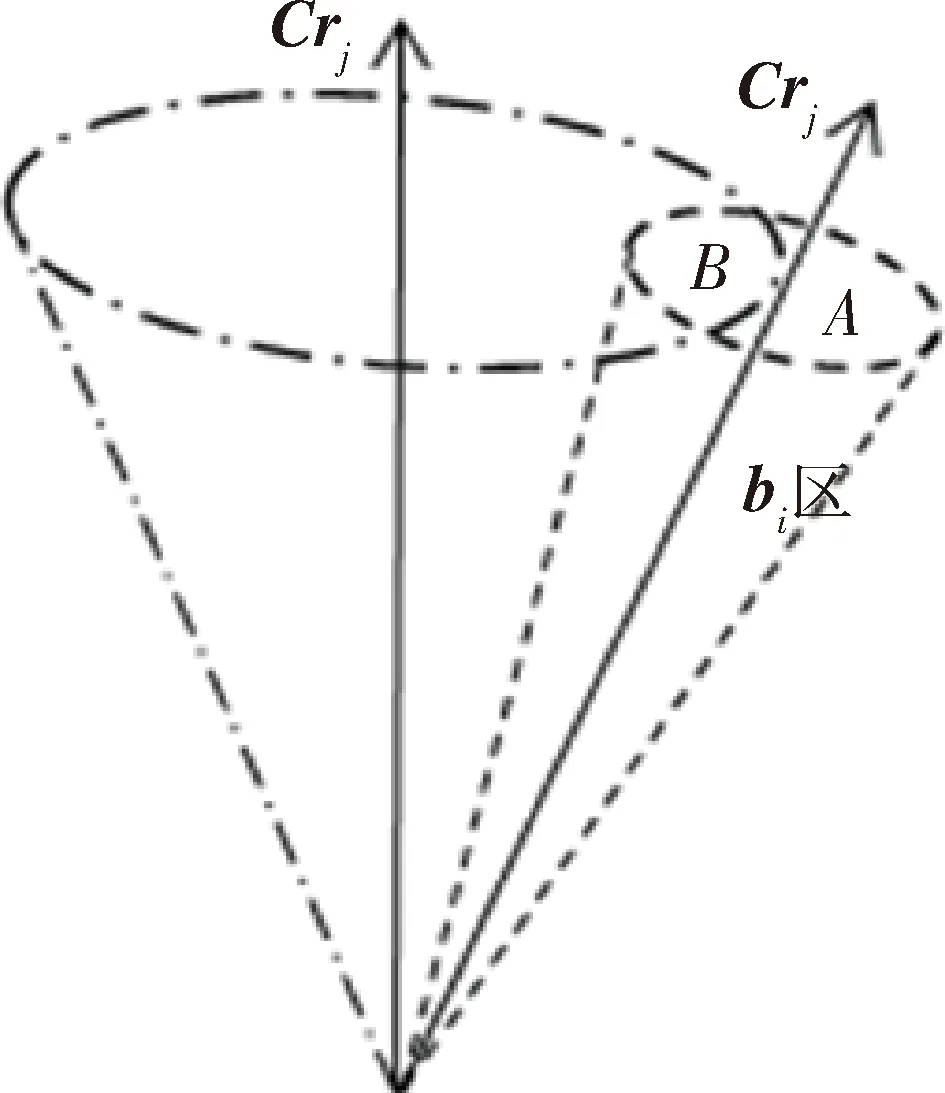
图2 性质的几何说明示意图Fig.2 Geometric explanation of characters

2 修正算法和效果评估

2.1 修正方案

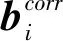
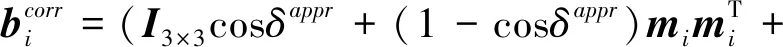
(14)

其中

(15)

2.2 修正算法

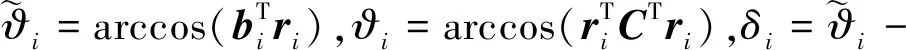
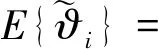
(16)

有

(17)

若δi为小量，假设

E{sinδi}=E{δi}

(18)

(19)

则修正角误差均值为

(20)

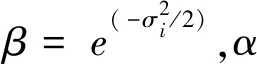
2.3 修正方法检验

根据上述修正角计算方法，对修正角效果进行评估.图3所示为修正角误差曲线.横坐标为理想修正角δideal(即当前实际指向ri与期望指向Cri的夹角αideal)与指向估计误差均方差σ(即测量值误差统计值)的比值，表征当前实际指向与期望指向的接近程度；纵坐标为修正角误差ε与指向估计误差均方差σ的比值，表征对控制量的修正精度.其中，ε分为真实修正角误差εreal、理论修正角误差εtheo、近似修正角误差εappr.

(1)真实修正角误差εreal

图3中每个“*”号点表示，由30000次测量产生的修正角的误差均值.即每次测量所得指向bi与期望指向夹角uideal的夹角αmeas、与当前实际指向Cri与期望指向夹角ri的夹角αreal的差值Δα，取均值Δαmean，与指向估计误差均方差σ的比值，得到真实修正角误差εreal.

(2)理论修正角误差εtheo

图3中实线是由式(20)计算所得δtheo，其中取α=1.25，δtheo称为理论修正角.理论修正角对真实修正角拟合情况如图所示，式(20)能够解析表示误差变化.

(3)近似修正角误差εappr

图3中虚线是由式(20)计算所得δappr，需要注意理论修正与近似修正的区别.理论修正是指用实际指向矢量Cri修正，近似修正是指用测量获得的矢量bi进行修正.

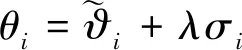
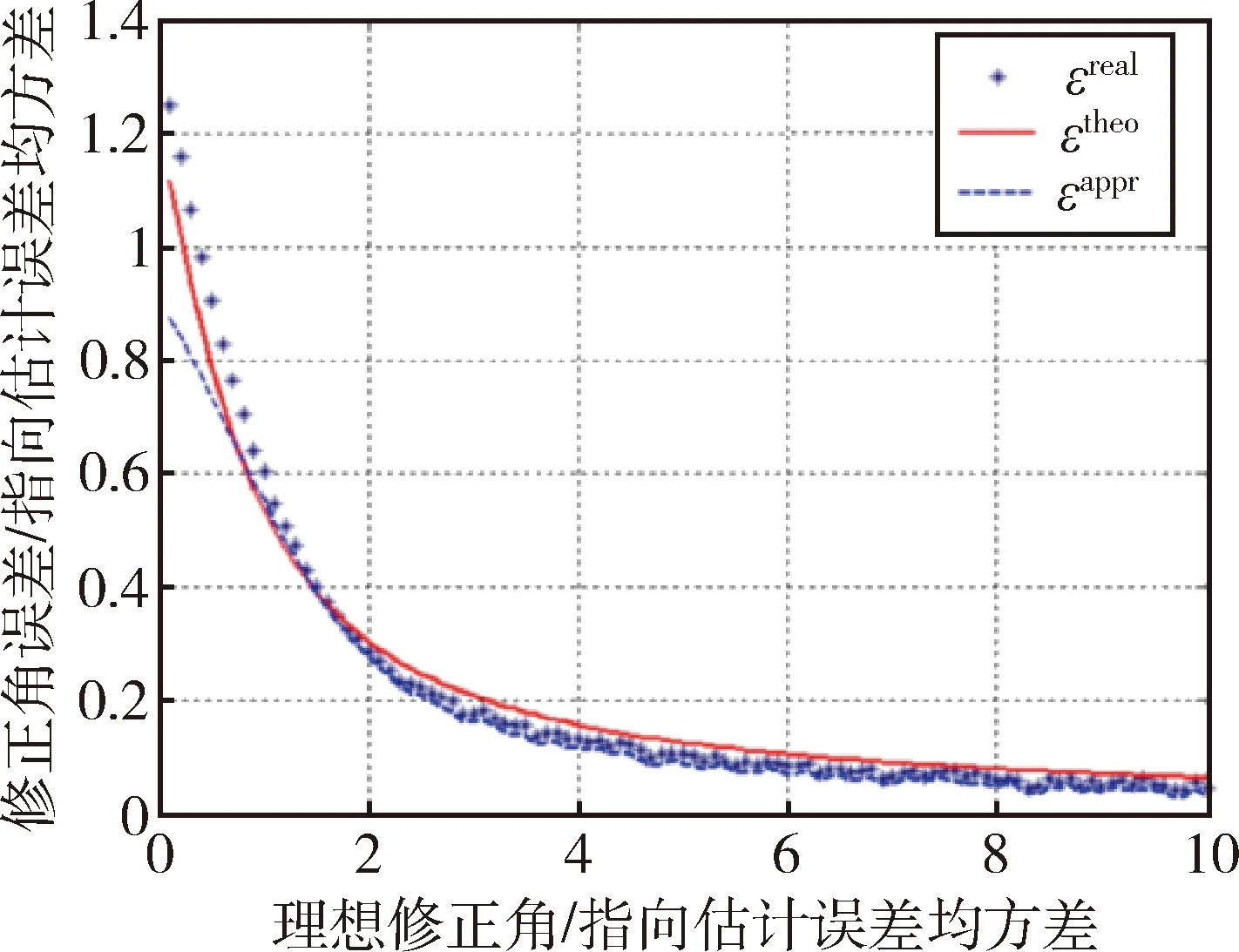
图3 修正方法检验曲线图Fig.3 Verification of correction method

2.4 修正效果分析

通过随机运动和正弦曲线运动产生的扰动，模拟分析对控制量的修正效果.此处运动是指受扰动后一级或二级平台指向与期望指向夹角变化.对于随机运动扰动，其计算结果与图3所示曲线相同.若模拟运动为正弦曲线，ϑi=Asin(ωt)，数值计算结果如图4所示，各坐标轴分别表示振幅变化、采样时间变化和修正误差均值变化.采样时间是指在正弦曲线在其过零点附近所取统计时间长度.自上而下三层数据分别为不加修正、近似修正和理论修正后控制量误差均值.图4所示修正效果规律和图3在趋势上一致，当统计时间较短、振幅较小时，期望指向和实际指向夹角也较小，修正效果明显.当统计时间增长时，修正效果急剧降低，这是由于夹角按正弦曲线变化增大导致的.

下面给出一个简单算例.假设σ=50 μrad，A=500 μrad，ω=π/3600.若统计时间t=1200 s，不加修正、近似修正和理论修正后误差均值分别为40 μrad、35 μrad和32 μrad，均方差为31 μrad、27 μrad和25 μrad.若统计时间t=120 s，则误差均值分别为56 μrad、35 μrad和26 μrad，均方差为33 μrad、28 μrad和20 μrad.

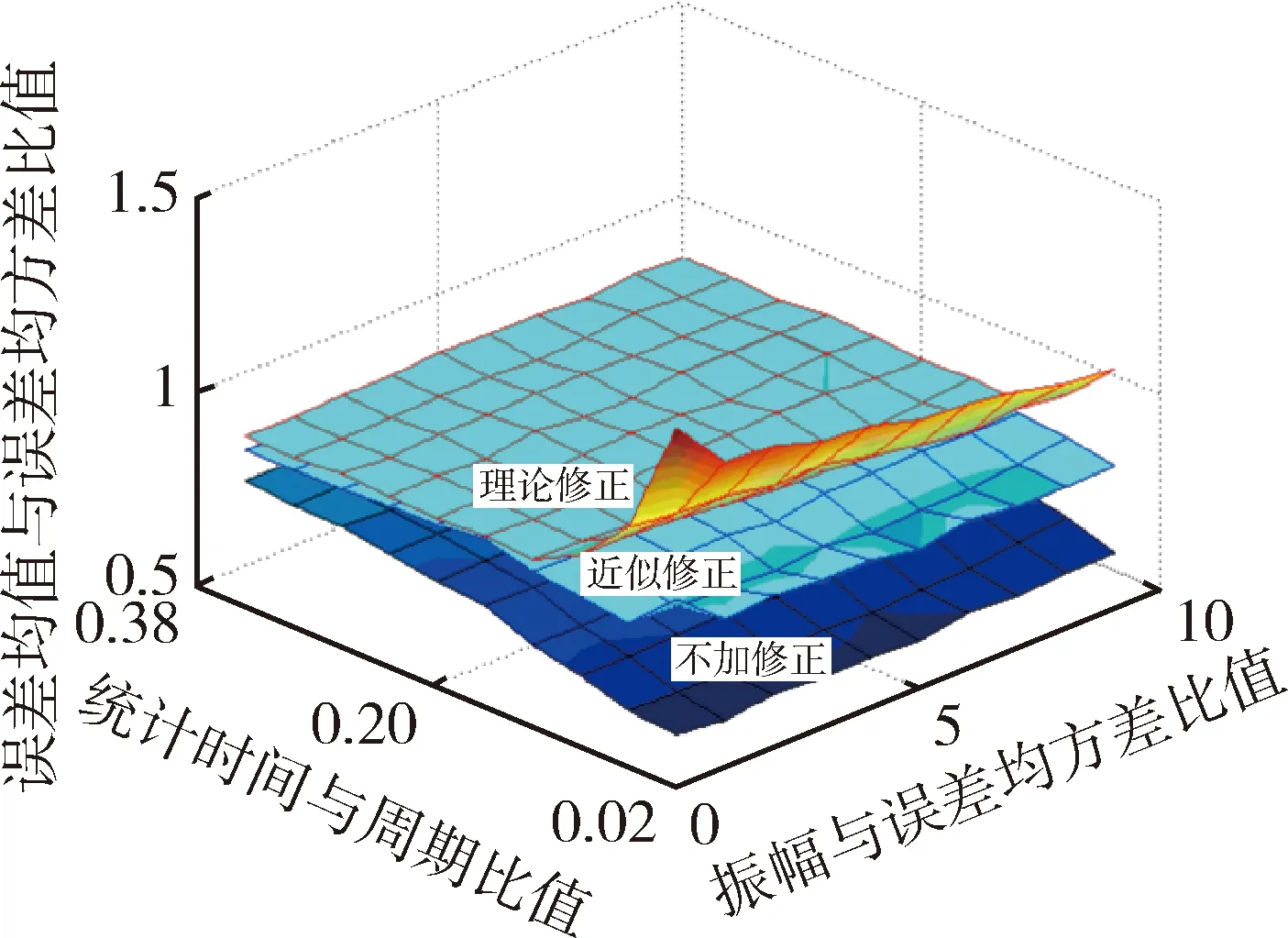
图4 正弦曲线模拟运动修正效果Fig.4 Correction effects under sine function simulated motion

3 控制-测量修正联合仿真校验

前文所述修正算法中控制量偏差由测量矢量绕实际矢量获得，而指向误差可以由绕3个姿态轴生成的姿态误差矩阵获得，令Cri为实际指向，bi为测量指向，Δi为测量误差矩阵，当姿态估计误差较小时，有

bi=ΔiCri≈(I3×3-[wi×])Cri

(21)

其中，wi=[δφiδθiδψi]T，δφi、δθi和δψi为绕姿态轴估计误差.式(19)所表示的观测方程与式(1)是相同的，故对姿态运动测量产生的控制量误差可以直接使用上述修正算法.

假设卫星运行于地球静止轨道，本体采用比例微分控制，卫星转动惯量、载荷转动惯量和转动机构转动惯量分别取为diag{1900,1800,2300}kg·m2，diag{0.02,0.04,0.06}kg·m2，diag{0.4,0.1,0.4}kg·m2，太阳帆板表面积10 m2，转动惯量55 kg·m2，姿态估计误差均方差为20 μrad，仿真时间为3000 s.

基于上述典型参数为卫星控制-测量修正联合仿真，所得到结果如下：不加修正、近似修正和理论修正后误差均值分别为21 μrad、15 μrad和11μrad；均方差分别为13 μrad、11 μrad和9 μrad.图5所示为仿真周期内误差统计，每1s记数30次.从图中可以直观看出加入修正后精度在统计意义上更优.修正后偏差仍大于理论修正，可以通过调节参数α和λ，或者对θi进行分段计算，以获取更好的修正.

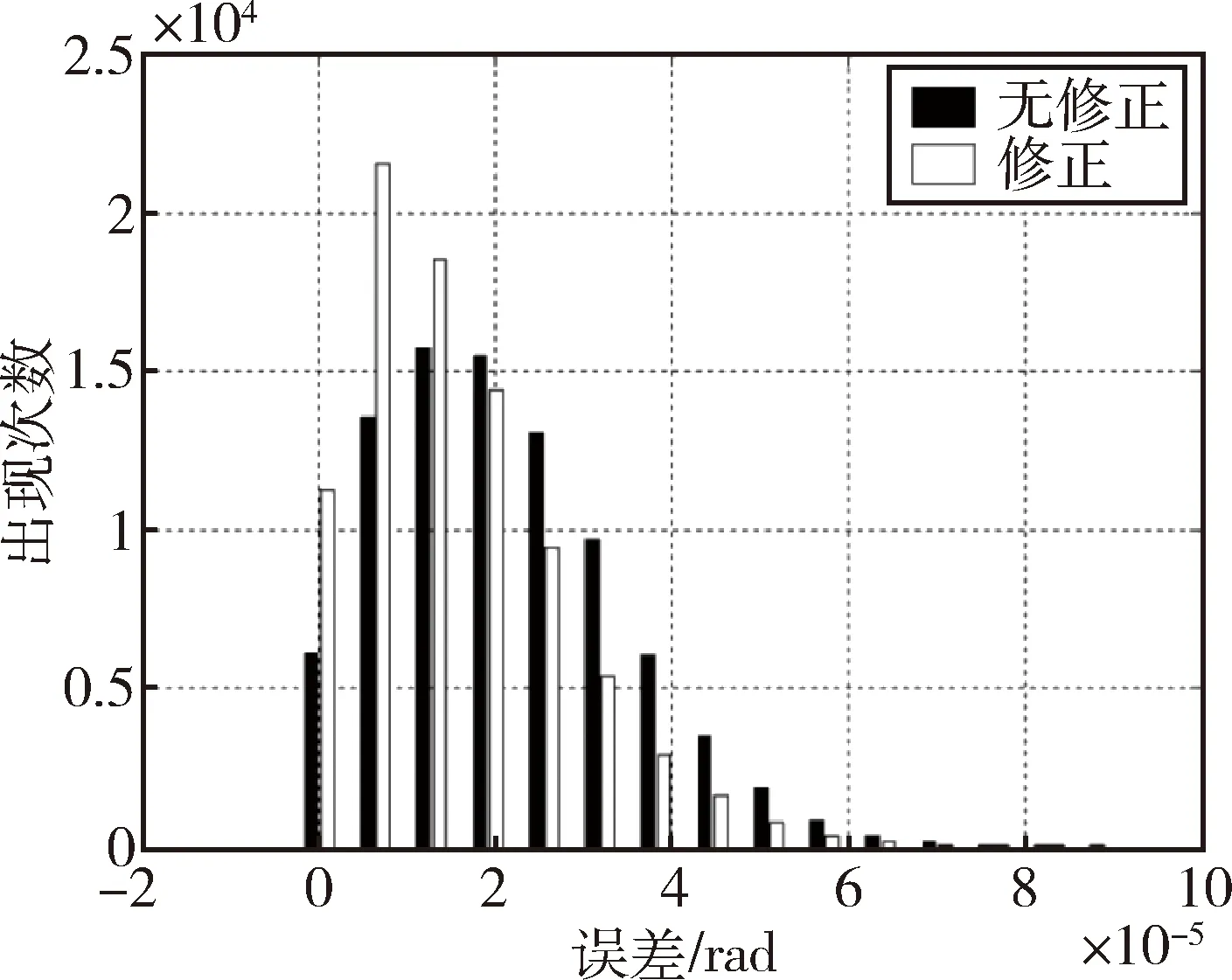
图5 姿态扰动修正精度比较Fig.5 Comparing of compensation accuracy for attitude disturbances

4 结 论

在空间平台火控系统中，对指向精度的要求是重要指标之一.在现有指向控制量输入模型中，由加法观测模型线性化所产生的误差，会对高精度系统产生影响.对单位矢量的观测采用非线性乘法观测模型能够消除加法观测模型线性化带来的误差，并且乘法观测模型揭示了一个由于采用加法观测导致的代数计算与几何过程不匹配问题，即两组不同观测矢量间夹角的期望是有偏的.

该问题对星上载荷指向运动的控制量输入存在明显影响，可以通过计算修正角误差期望值加以修正.文中给出了理论修正的解析计算公式，但在轨实际应用中，无法使用该公式直接计算获得修正角，可以采用近似公式计算.通过数值仿真算例，验证了修正方法的有效性.

修正效果取决于期望指向和实际指向的夹角，与测量所得指向的误差的比例.比例越小，修正效果越明显.在轨应用中，适用于安装在高精高稳空间平台的转动火控系统.