大跨度曲线组合结构人行天桥设计与振动特性分析*

周 萌 王 琳 薛 准 魏晓晨 高劲洋 张屹垚 许立言 樊健生

(1.中冶建筑研究总院有限公司, 北京 100088； 2.清华大学, 北京 100084；3.珠海深圳清华大学研究员创新中心, 广东珠海 519080； 4.北京航空航天大学交通科学与工程学院, 北京 100191)

随着计算分析方法的进步和轻质高强材料的应用，桥梁设计不断向大跨、轻盈、柔性等方向发展。此类新结构在承载力、变形等静力性能指标上一般能满足结构设计和使用要求，制约此类新结构应用的是其动力性能、特别是人致激励下的振动问题[1]。对于大跨人行天桥，当结构自振频率接近人行步频时，桥面会发生明显的振动响应，从而对桥上行人的使用舒适度造成影响，同时也使结构面临倒塌的风险[2]。

对人行振动舒适度的研究最早可追溯至二十世纪初期，Reither和Meister在不同外部激励条件下对卧姿、坐姿、站姿等不同姿态的行人舒适度进行了试验研究，将人对振动的感觉分为6个等级：无感觉、稍有感觉、明显感觉、使人厌烦、使人不悦、不可忍受[3]。Mallock对人体在振动环境下的舒适度进行了定量研究并得出结论：当结构加速度响应超过1.0 m/s2时，人体感到无法接受；当结构物加速度响应超过0.5 m/s2时，人体感觉到不舒适；当结构物加速度响应小于0.1 m/s2时，人体无法感受到[4]。Dieckmann研究则认为人体共振频率在5 Hz附近，在此范围内行人能忍受的结构加速度限值最小[5]。Irwin基于前人大量的试验结果和自己的实测数据，提出将加速度均方差作为舒适度的评价标准[6]。从上述研究可见，行人对结构振动的舒适度感受具有较大的主观性。同时，行人的身体素质、行走方式、结构环境等因素也会对舒适度评价造成影响。

为避免结构振动对行人带来的不舒适感，我国CJJ 69—95《城市人行天桥与人行地道技术规范》[7]规定：天桥上部结构竖向自振频率不应小于3 Hz。但该规范对较柔的人行桥要求过于严格，且未考虑人行桥的横向振动，无法保证工程设计的合理性和有效性。

除避开敏感自振频率外，人行天桥舒适度还可通过限制结构的动力响应来保证。英国规范BS 5400[8]、德国规范EN 03[9]等欧美国家规范在评价桥梁振动舒适度时，采用行人步行激励，然后将结构振动的速度和加速度响应与人振动舒适度阈值进行比较，从而确定结构的动力性能是否满足使用的要求。这种方法将结构自身质量、刚度、阻尼以及外界荷载激励条件考虑在内，相较于国内规范更为详细、合理。近年来，许多学者将加速度响应作为舒适度评价体系的重要指标，并提出了评估大跨结构的振动加速度响应的有效方法。杨娜等采用人群集度荷载模型预测大跨结构在人群荷载作用下的加速度响应，适用的工况范围较广[10]。谢伟平等[11]基于自激励人体模型，分析了人-桥竖向相互作用的变化规律及影响因素，研究表明结构固有频率和人与结构质量之比对人-结构相互作用有较大影响。操礼林等通过研究人群协同性对结构人致振动的影响，建立了考虑行人同步率的随机行走人群模型，其可准确反映人群行走荷载对人行天桥的实际作用、并合理评估桥梁结构的人致振动响应特征[12]。

本文以珠海市情侣路香炉湾城市阳台大跨度曲线人行天桥项目为背景进行分析与设计。介绍了针对大跨度、大曲率异型桥梁所采用的钢-混凝土组合连续梁桥方案，利用有限元软件ANSYS对结构施工过程及成桥阶段中应力、挠度等关键设计指标进行分析和验算。根据国内外设计规范对结构的动力性能进行了分析，结合规范指标对人行天桥的舒适度进行了评估。进而提出使用多重调谐质量阻尼器(MTMD)的减振方案，为大跨度曲线人行桥的工程设计提供参考。

1 工程概况

珠海市情侣路香炉湾城市阳台项目作为综合性开放式公园，是情侣路“城-海”沿线的核心景观风貌的重要节点。如图1所示，情侣路城市阳台人行天桥连接了道路的人行系统，是代表珠海慢行系统和城市文化发展的一项标志性工程。

a—城市阳台人行天桥总体平面布置；b—人行天桥俯视视角；c—人行天桥平视视角。图1 珠海城市阳台人行天桥建筑效果Fig.1 Renderings of pedestrian bridge of City Balcony project in Zhuhai

从打造情侣路城市阳台人行天桥的全方位观景平台并兼顾缓解交通干道通行压力的角度出发，该项目采用了“又”字形的复杂曲线平面布置，桥梁全长151 m，最大净跨度36.5 m，桥面宽3.4～8.9 m不等，总面积890 m2。同时结构希望通过尽可能降低界面高度促进桥梁与环境的融合，减小对步行道上过路行人的压迫感和对自然环境产生的突兀感。为实现上述功能目标，城市阳台人行天桥采用如图1所示的钢-混凝土组合连续梁桥的总体结构方案，充分发挥了混凝土和钢材两者的性能优势，形成具有优越力学性能的桥梁结构体系[13]。

如图2所示，按照下部结构墩柱以及下部支承桁架的位置，可将全桥分为主跨段、悬挑段、梯道段1、梯道段2、梯道段3。主跨段为钢箱梁-钢桁架复合结构，净跨36.5 m，总长度46.6 m；悬挑段同为钢箱梁-钢桁架复合结构，净悬挑10.2 m，总长48.8 m；梯道段1～3均为钢箱梁结构，长度分别为15.3，20.0，20.0 m。

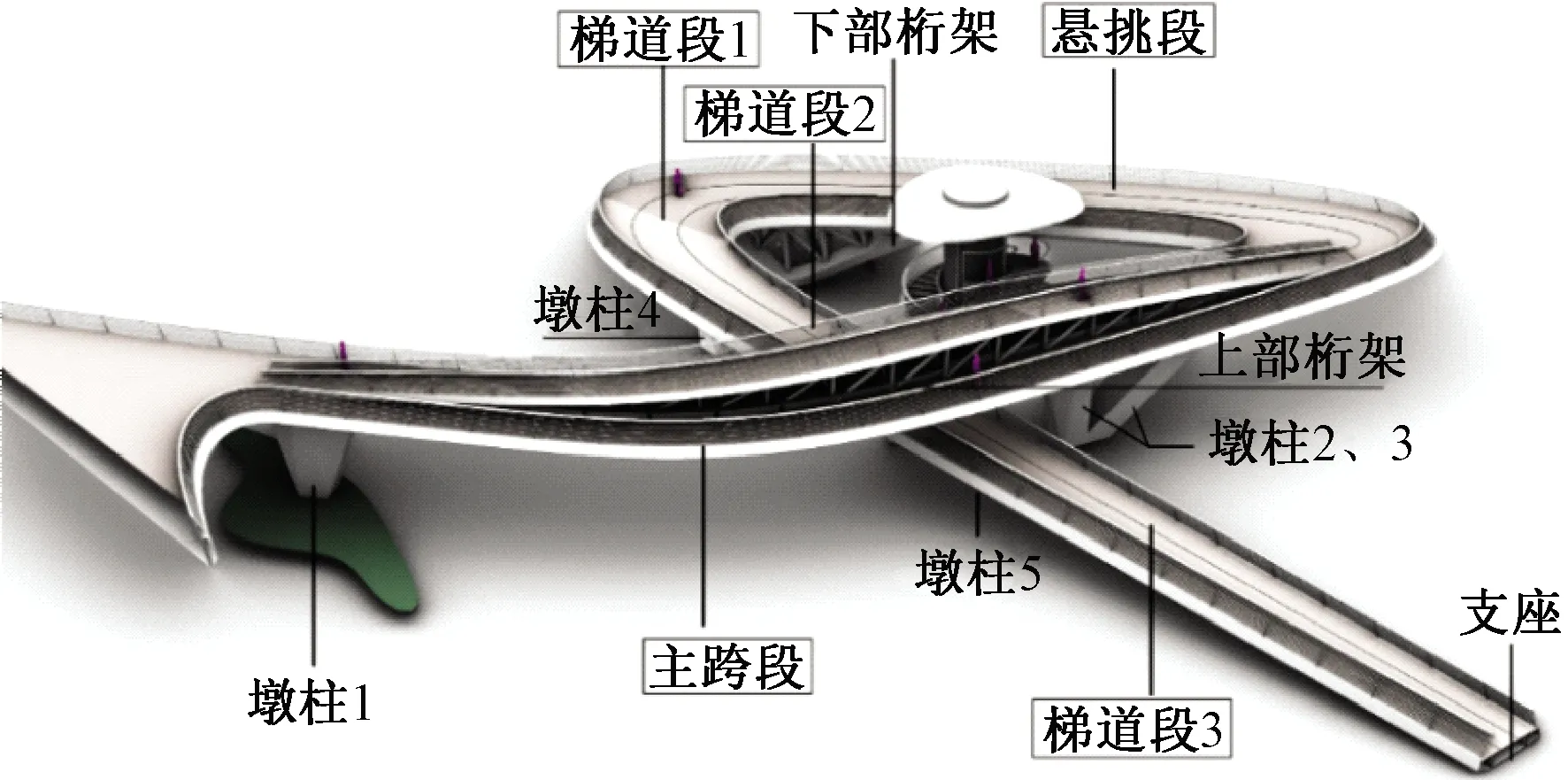
图2 人行天桥结构分段示意Fig.2 The segmentation schematic diagram of the pedestrian bridge structure

桥梁空间造型复杂，其大跨度曲线型布置以及大悬挑区段均对结构设计提出了挑战，为有效提高结构刚度、减轻结构自重、降低结构高度，主梁截面采用如图3所示的钢箱梁-超高性能混凝土(UHPC)组合截面。

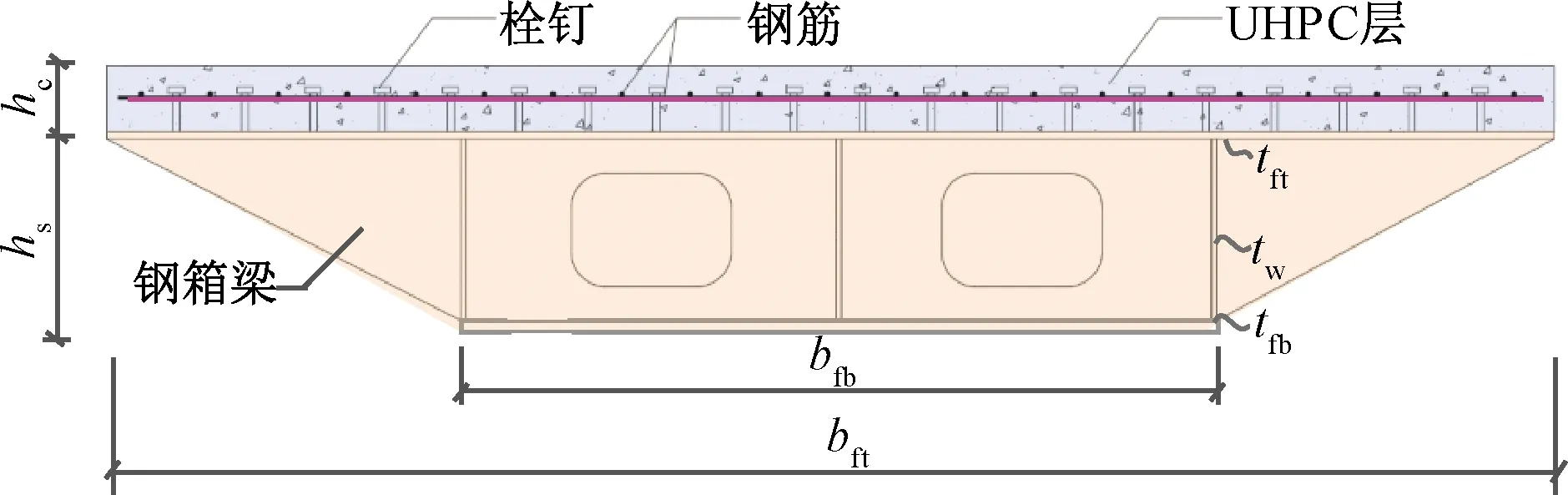
图3 主梁组合箱梁截面示意Fig.3 Schematic diagram of the cross section for the main composite box girder

组合钢箱梁使用栓钉作为抗剪连接件，栓钉直径13 mm，高度35 mm，布置间距为200 mm，栓钉与钢箱梁顶板焊接，沿全桥均匀布置。栓钉材料性能等级为4.6级，栓钉极限抗拉强度取fu=400 MPa。钢箱梁顶板宽度bft随桥形变化，为3.4～8.9 m不等，顶板厚度tft为30 mm。底板宽度bfb同样随桥形变化，为1.35～5.6 m不等，底板厚度tfb为30 mm。箱梁腹板厚度tw为16 mm，箱梁梁高hs采用变高度设置，主跨段梁高为0.8 m，悬挑段梁高1.1 m，梯道段梁高由1.1 m渐变为落地端的0.5 m，不同节段间梁高采用线性变化。

对于本桥桥墩，为避免侵占下部人行道空间，设置墩柱位置及编号如图4所示。其中，墩柱1为钢管柱，墩柱2～墩柱5为钢管混凝土柱，混凝土强度等级为C50。墩柱2～4顶部钢管与钢箱梁通过焊接刚性连接，墩柱1、5顶部设置橡胶支座简支连接，梯道段端部落地处同样设置橡胶支座简支连接。所有墩柱柱脚均与基础刚接，下部桁架落地支承处同样与基础刚接。

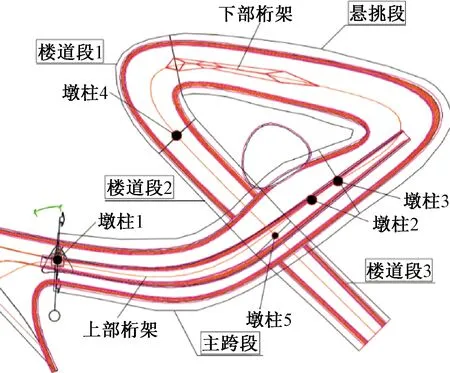
图4 墩柱位置及编号Fig.4 Location and number of piers

对于钢箱梁-钢桁架复合结构的桁架部分，其上部桁架杆件采用圆钢管，杆件可分为三类：竖向腹杆、斜腹杆以及连接两榀桁架的腹杆，不设置水平弦杆，杆件布置如图5所示。对于不同杆件，根据其所受内力大小，分别给出两种截面尺寸。上部桁架最高点左右各三格范围内，杆件内力较大，采用较大截面尺寸；其他位置的杆件采用较小截面尺寸。杆件间通过焊接进行连接，上部桁架杆件底部焊接于桥面板的纵、横隔板交点处。

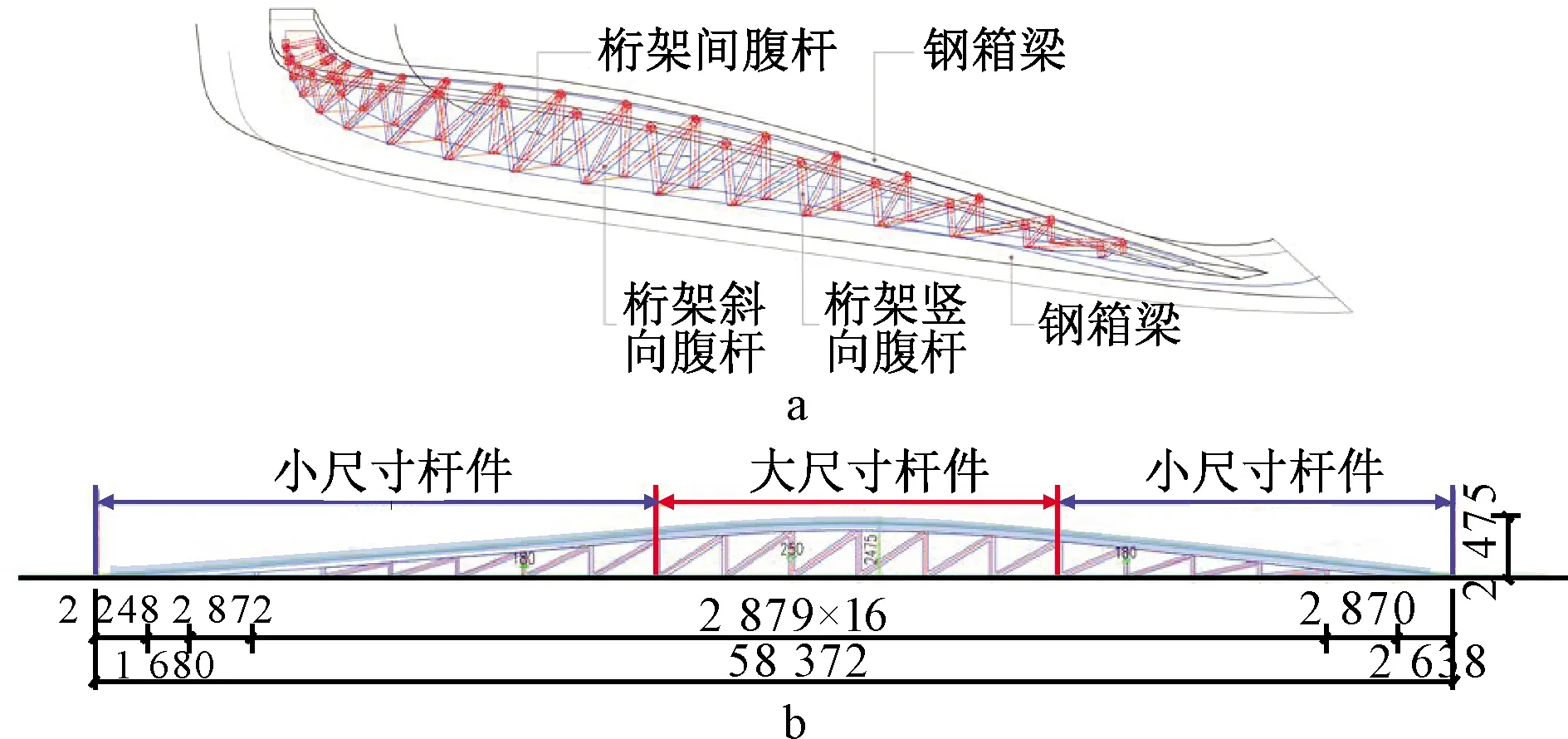
a—桁架结构的杆件分类；b—桁架杆件的截面分类，mm。图5 上部桁架杆件布置Fig.5 Arrangements of upper truss members

上部桁架顶部同样设置钢箱梁，用于承受二层步道的人行荷载。钢箱梁高度为300 mm，顶、底板厚度为20 mm，其宽度随桥梁线形变化，平均宽度约2.4 m，腹板厚度16 mm。箱梁截面中间设置一道纵隔板，厚度为16 mm，每隔2.5 m左右设置一道横隔板，其厚度为10 mm。对于钢箱梁底板与桁架杆件连接处，局部应设置加劲肋。箱梁的典型截面图6所示。

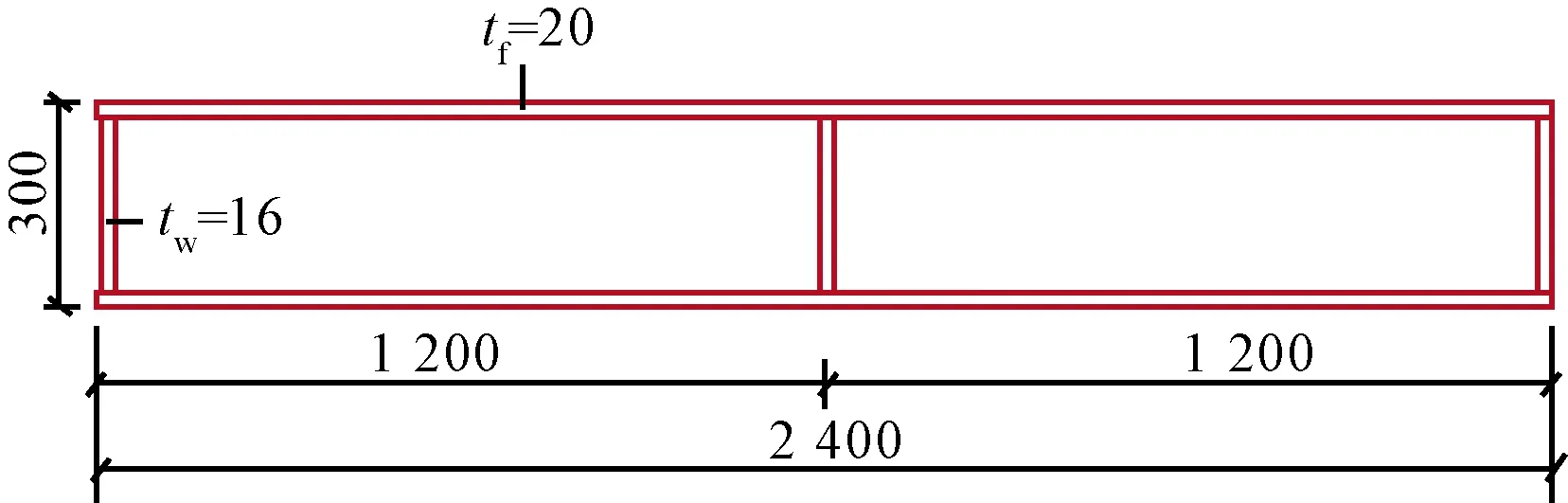
图6 上部桁架钢箱梁截面示意 mmFig.6 The section diagram of upper truss steel box girder

下部桁架的作用是协助墩柱支承悬挑段主梁(图7)，其弦杆采用方钢管，截面尺寸为1 000 mm×1 000 mm，壁厚30 mm；腹杆采用圆钢管，所有腹杆尺寸相同，直径273 mm，壁厚20 mm。杆件间通过焊接进行连接，下部桁架落地点与基础刚接。全桥钢主梁、纵(横)隔板、加劲肋、钢桁架、钢柱等均采用Q355QC级钢材，在工厂分节段制作完成，运输到现场后进行焊接拼装。

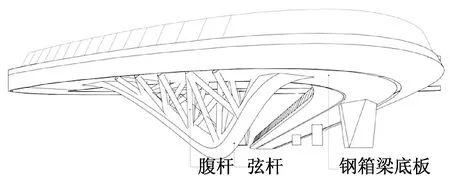
图7 下部桁架结构的立体示意Fig.7 The stereoscopic diagram of the lower truss structure

2 有限元模型及静力分析结果

采用通用有限元软件ANSYS对主桥结构进行受力分析。主桥结构的静力计算包括施工阶段和运营阶段，计算中根据JTG D60—2015《公路桥涵设计通用规范》[16]相关规定进行内力组合和应力安全验算。

2.1 有限元模型

图8为建立的全桥有限元模型，其中主梁顶底板、腹板、纵横隔板以及上部人行桁架钢箱梁板件均采用Shell 63壳单元，UHPC层也采用壳单元Shell 63，墩柱及桁架杆件采用Beam 188梁单元。墩柱顶部结点与主梁下翼缘对应范围内的结点采用所有自由度耦合的方式模拟梁柱的刚接，柱脚结点约束所有自由度，天桥两端释放沿桥梁纵向的位移自由度。主梁上下翼缘及桥面板采用三角形网格，腹板及纵横隔板采用四边形网格，所有壳单元及梁单元的网格尺寸均为0.2 m。模型中不考虑加劲肋的作用。其中假设组合梁在完全剪力连接设计条件下UHPC层与钢箱梁能够共同工作并忽略钢-混界面的滑移，UHPC与钢箱梁顶板采用共结点的方式进行连接。

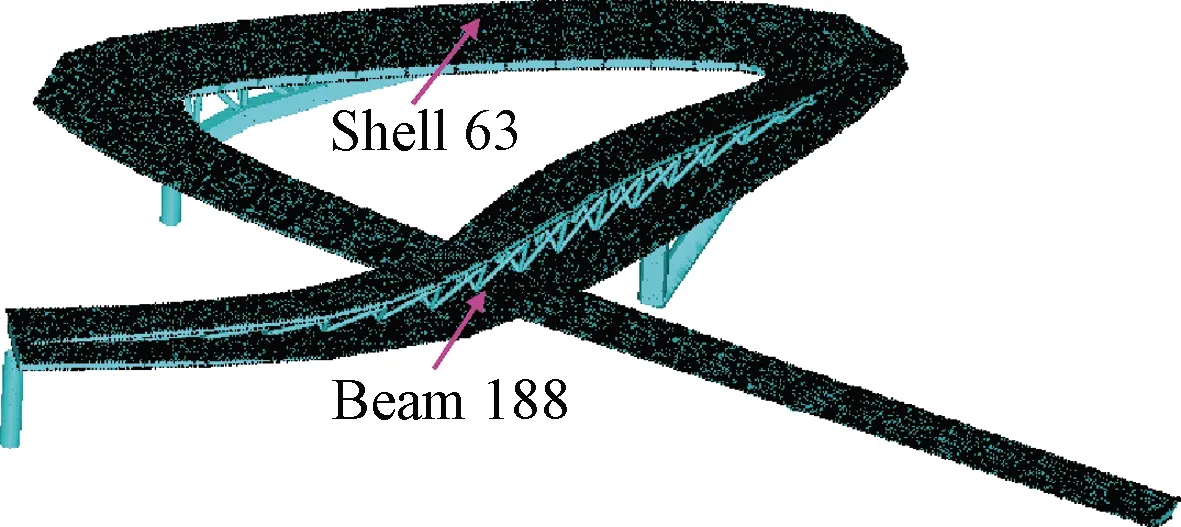
图8 桥梁结构的三维有限元模型Fig.8 3D finite element model of bridge structure

2.2 施工阶段受力性能分析

2.2.1 施工阶段定义

钢箱梁按照图9所示分割为11个节段(图中黑线为节段分割线)，其中主跨段分3个节段，悬挑段分4个节段，梯道段1～3共4个节段。考虑到节段运输与施工，控制各节段长度不超过16.5 m。

各节段在工厂预制完成后运输至现场，依据图10所示施工顺序进行吊装拼接，全桥不同节段间顶板、底板及腹板均采用焊接连接。同一位置的临时支撑包含两道，分别布置于钢箱梁两腹板内侧(图9中红圈)。布置临时支撑处应考虑局部承压，并采取相应构造措施，如设置加劲肋等。根据该工程的施工工序，在有限元软件中定义的施工阶段信息见表1。

表1 施工阶段定义Table 1 Definition of construction stage

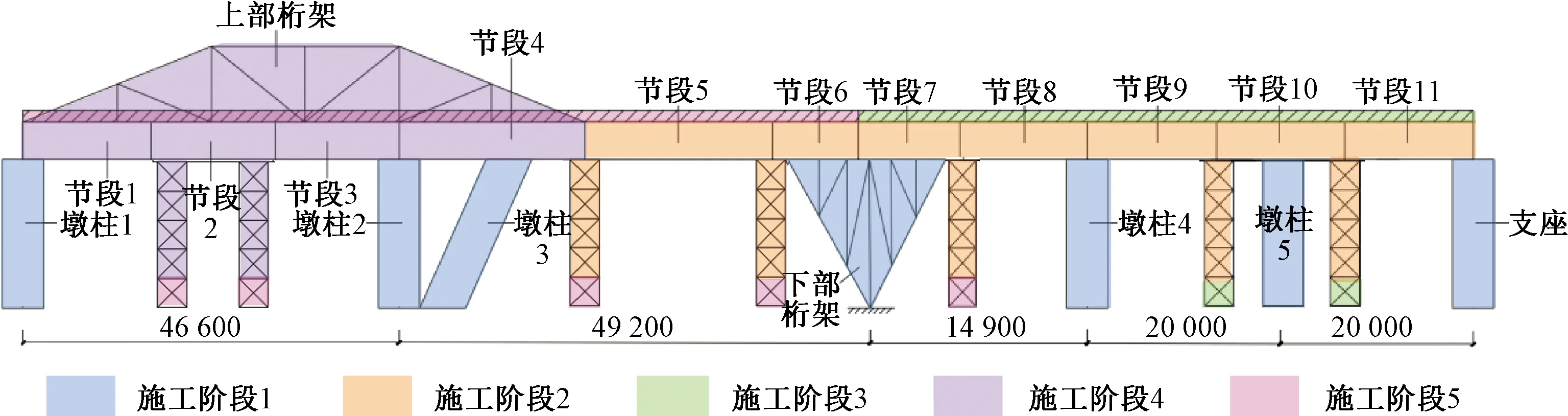
图10 结构施工顺序示意 mmFig.10 The schematic diagram of construction sequence of the structure

2.2.2 施工阶段计算结果

经计算得到钢结构部分在各施工阶段的应力水平包络图，选取钢箱梁底板、主跨桁架底板以及主跨桁架腹板的代表性计算结果，如图11所示。结果表明钢梁在施工阶段的最大von Mises应力为128 MPa，出现在主跨桁架腹板处，可见施工阶段结构整体应力水平较低，不起控制作用。

a—钢箱梁底板；b—主跨桁架底板；c—主跨桁架腹板。图11 施工阶段钢结构应力水平 MPaFig.11 Stress distribution of the steel structure in construction stage

图12为全桥在施工阶段的竖向变形包络云图。由图中结果可知：施工阶段主跨段最大挠度为43.0 mm，悬挑最大挠度为27.5 mm。施工阶段产生的竖向挠度可以通过预拱度抵消，在本项目中为减小主梁在正常使用阶段出现过大挠曲变形，钢箱梁在工厂制作时按照恒载+1/2静活载作用下的主梁挠度预先设置预拱度。

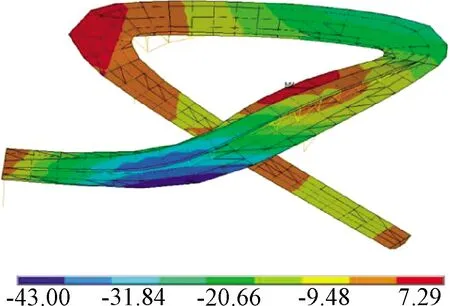
图12 施工阶段钢结构竖向位移 mmFig.12 Vertical displacement of the steel structure in construction stage

2.3 成桥状态受力性能分析

2.3.1 成桥状态承载力验算

根据CJJ 69—95，人行天桥在成桥阶段承受的荷载作用主要包括永久荷载(结构自重、二期恒载、基础沉降)，可变荷载(人群荷载、风荷载、温度荷载)，以及偶然荷载(地震作用、汽车撞击力)。具体荷载取值见表2。

桥梁承载能力极限状态验算按JTG D60—2015考虑基本组合、偶然组合、地震组合，对各种荷载工况进行最不利组合。图13为钢结构部分的应力水平包络图，选取钢箱梁的底板和隔板以及主跨桁架底板和腹板的代表性计算结果：其中主梁上、下翼缘的最大应力为196 MPa，腹板及纵横隔板最大应力为254 MPa，腹板及隔板在桥墩位置发生明显的应力集中现象。主跨段桁架的上部钢箱梁翼缘最大应力为199 MPa，腹板及隔板最大应力为261 MPa，有明显应力集中现象。总体上主桥应力值小于设计抗拉强度，满足承载力要求。

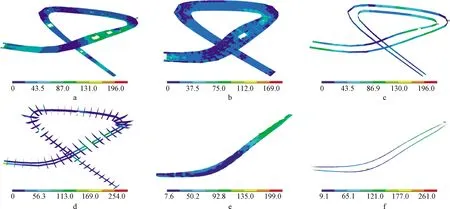
a—钢箱梁底板; b—钢箱梁顶板； c—钢箱梁腹板; d—钢箱梁隔板； e—主桁架底板; f—主桁架腹板。图13 成桥阶段钢结构应力包络图 MPaFig.13 Stress envelope diagrams of the steel structure in post construction stage

2.3.2 成桥状态变形验算

城市阳台人行天桥为大跨度、大曲率曲线异型桥，主跨跨中及悬挑段跨度大、变形大，因此主梁采用了钢-混凝土组合结构形式，特别是在主跨和悬挑段的钢梁部分采用了钢箱梁-钢桁架复合结构形式。考虑不同的人群荷载布置方式，挠度验算可分为三种工况：1)工况1，1.0全桥满布人群荷载+1.0其他活荷载；2)工况2，1.0主跨段人群荷载+1.0其他活荷载；3)工况3，1.0悬挑段人群荷载+1.0其他活荷载。

对以上三种工况计算结果取包络，可以得到主跨段跨中最大挠度为24.2 mm，悬挑段最大挠度为24.1 mm。其他位置挠度小、无需验算。根据CJJ 69—95，由人群荷载产生的竖向挠度为：梁板式主梁跨中，取1/600计算跨径；梁板式主梁悬臂端，取1/300悬臂长度。本工程主跨段计算跨径为36.5 m，挠度限值60.8 mm>24.2 mm；净悬挑10.2 m，挠度限值34.0 mm>24.1 mm。全桥的挠度验算均符合CJJ 69—95的要求。

2.3.3 成桥状态混凝土抗裂验算

针对组合梁UHPC桥面板的抗裂验算，可根据JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》将桥面板作为矩形截面钢筋混凝土受弯构件，按照式(1)计算全桥负弯矩区的最大裂缝宽度。

(1)

式中：Wcr为最大裂缝宽度，与钢筋应力σss、钢筋弹性模量Es、最外排纵向受拉钢筋的混凝土保护层厚度c、纵向受拉钢筋直径d、纵向受拉钢筋的有效配筋率ρte有关；此外,C1为钢筋表面形状系数、C2为长期效应影响系数、C3为构件受力性质有关的系数。

裂缝宽度验算应按荷载短期效应组合并考虑长期效应的影响，其引起开裂截面的纵向受拉钢筋应力σss按式(2)计算：

(2)

式中：Ms为验算截面按作用频遇组合计算的弯矩值；As为受拉区纵向钢筋截面面积；h0为截面有效高度。

根据如图14所示的有限元模型计算结果，UHPC桥面板应力最大位置位于节段3和节段4的拼接截面，忽略结构明显的应力集中区域，对危险截面的裂缝宽度验算结果如表3所示。结果表明：主桥结构在正常运营阶段主桥结构混凝土桥面板负弯wmax为裂缝宽度计算最大值；wlim为裂缝宽度规范验算限值。

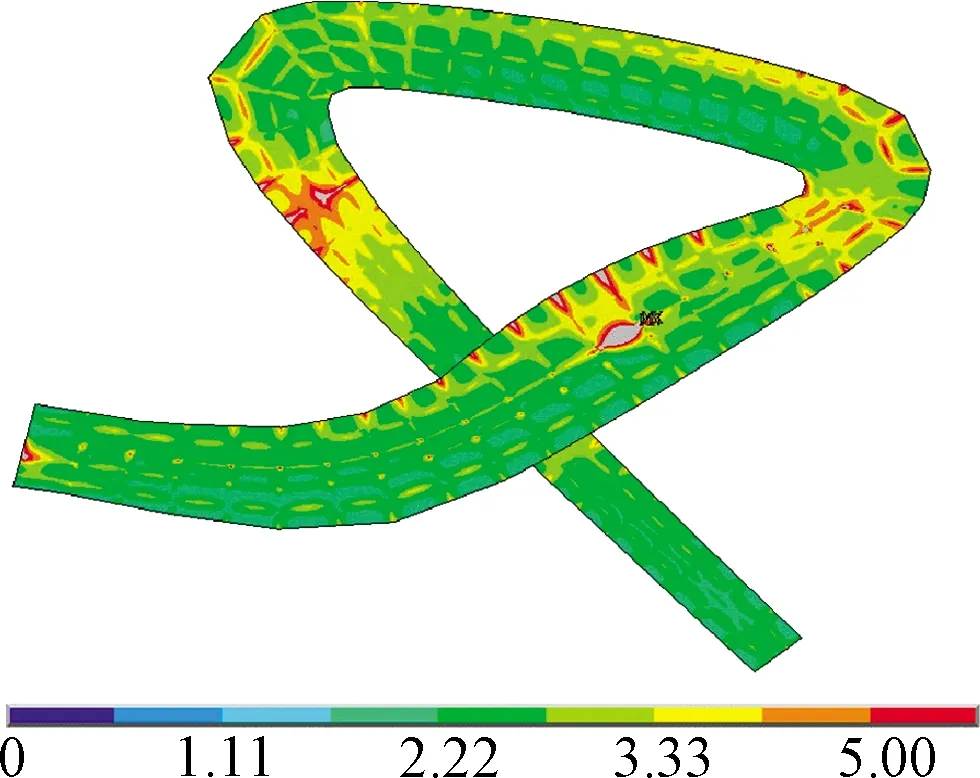
图14 作用频遇值组合下成桥阶段UHPC板主拉应力 MPaFig.14 Principal tensile stress distribution in UHPC slab under the combination action of frequent values

表3 混凝土板裂缝宽度验算Table 3 Checking calculation of crack width in concrete slab

矩区的裂缝宽度均小于JTG 3362—2018限值0.15 mm，满足设计要求。

3 振动及舒适度验算

为保证行人激励下人行天桥的舒适度要求，现行的各国规范主要用两种方法解决人行天桥的振动问题：避开敏感频率法和限制动力响应值法。

避开敏感频率法就是指通过改变结构的刚度使结构基频在行人步行频率范围之外，避免桥梁在行人步行力激励下发生共振。我国CJJ 69—95规定桥梁第一阶竖向频率必须大于3 Hz；日本道路协会规定人行桥的竖向自振频率不应落在1.5～2.3 Hz范围之内；瑞士SIA 160[17]要求人行桥的竖向振动固有频率要避免落入1.6～2.4 Hz和3.5～4.8 Hz；欧洲EN 1990∶2002[18]及加拿大OHBDC[19]等规范规定桥梁竖向第一阶自振频率超过5 Hz时结构舒适度即可满足要求，也属于避开敏感频率法的范畴。此外欧洲EN 1990∶2002对天桥的侧向自振频率也有相关要求：侧向第一阶自振频率需超过2.5 Hz才无需验算结构的侧向振动响应。一般情况下，避开敏感频率法可以满足大部分人行天桥的舒适度验算要求，但对于较柔的人行桥要求过于严格，这类人行桥的固有频率虽然不满足规范规定的频率要求，但其振动响应是在可接受范围内的。因此，避开敏感频率法对于部分工程可能偏于保守，不利于人行桥设计的合理性和有效性。

限制动力响应值法指当结构固有频率无法满足规范要求的频率范围时，需要验算桥梁在行人步行激励下的振动响应，确保桥梁振动的加速度响应在规定的限值之下，从而满足人行天桥的舒适度要求。欧盟EN 1990∶2002、英国BS 5400、德国EN 03等国外规范都建议采用限制动力响应值法评估人行桥的舒适度。

3.1 结构动力特性分析

以本工程为例，利用建立的ANSYS有限元模型进行模态分析，计算得到结构的前五阶自振频率及其变形模态如表4所示。

从表4可以看出，该人行天桥不满足我国CJJ 69—95中规定的第一阶竖向频率必须大于3 Hz这一硬性要求。考虑到德国《人行桥设计指南EN 03(2007)》(以下简称“德国规范”)对振动及舒适度的要求更能反映桥梁建成后的实际振动舒适度情况，因此本例同时参照德国规范对人行天桥的振动及舒适度进行分析验算。

表4 人行桥结构模态分析结果Table 4 Modal analysis results of the pedestrian bridge structure

3.2 人致振动响应分析

德国规范对行人舒适性指标的具体规定见表5。根据德国规范要求，结构一阶竖向自振频率为2.345 Hz，满足1.25 Hz≤fi≤2.4 Hz(fi为落在行人步频范围内的桥梁模态频率值)，位于竖向频率敏感范围，需进行人致振动响应分析。结构一阶横向自振频率为3.426 Hz，不满足0.5 Hz≤fi≤1.2 Hz，不在敏感范围内，认为结构横向振动满足要求。

表5 德国规范中的人行桥舒适度指标Table 5 Comfort indicators for pedestrian bridges in specification EN 03 m/s2

针对人行桥结构在竖向的人致振动响应特性，按照德国规范按如下两种设计工况进行计算。规范中给出步行荷载的表达式为：

p(t)=P·cos(2πfit)×n′ψ

(3)

式中：P为荷载幅值，对竖向振动，P=280 N；ψ为折减系数；n′为等效同步人群密度，1/m2，其计算方法如式(4)所示。

(4)

式中：ξ为结构阻尼比；S为加载面积；D为人群密度,1/m2；n为总行人数。

结合主跨及悬挑桥面面积等结果参数，确定结构分析工况中单位面积上竖向步行荷载取值以及对应舒适度级别见表6。

表6 人致振动分析工况及相应舒适度级别Table 6 Human-induced vibration analysis conditions and corresponding comfort levels

根据结构一阶振型，将工况一和工况二的步行荷载竖向简谐函数分别施加在振型计算模型上，施加形式如图15所示。

图15 步行谐波荷载的加载方式Fig.15 Loading mode of walking harmonic load

得到结构悬挑及主跨的最大竖向加速度响应值如图16所示。计算结果表明：1)工况一主跨最大竖向加速度为0.403 m/s2，小于加速度限值0.5 m/s2；悬挑最大竖向加速度为0.328 m/s2，小于加速度限值0.5 m/s2，可进行振动控制设计。2)工况二主跨最大竖向加速度为1.886 m/s2，大于加速度限值1.0 m/s2；悬挑最大竖向加速度为1.533 m/s2，大于加速度限值1.0 m/s2，需进行振动控制设计。

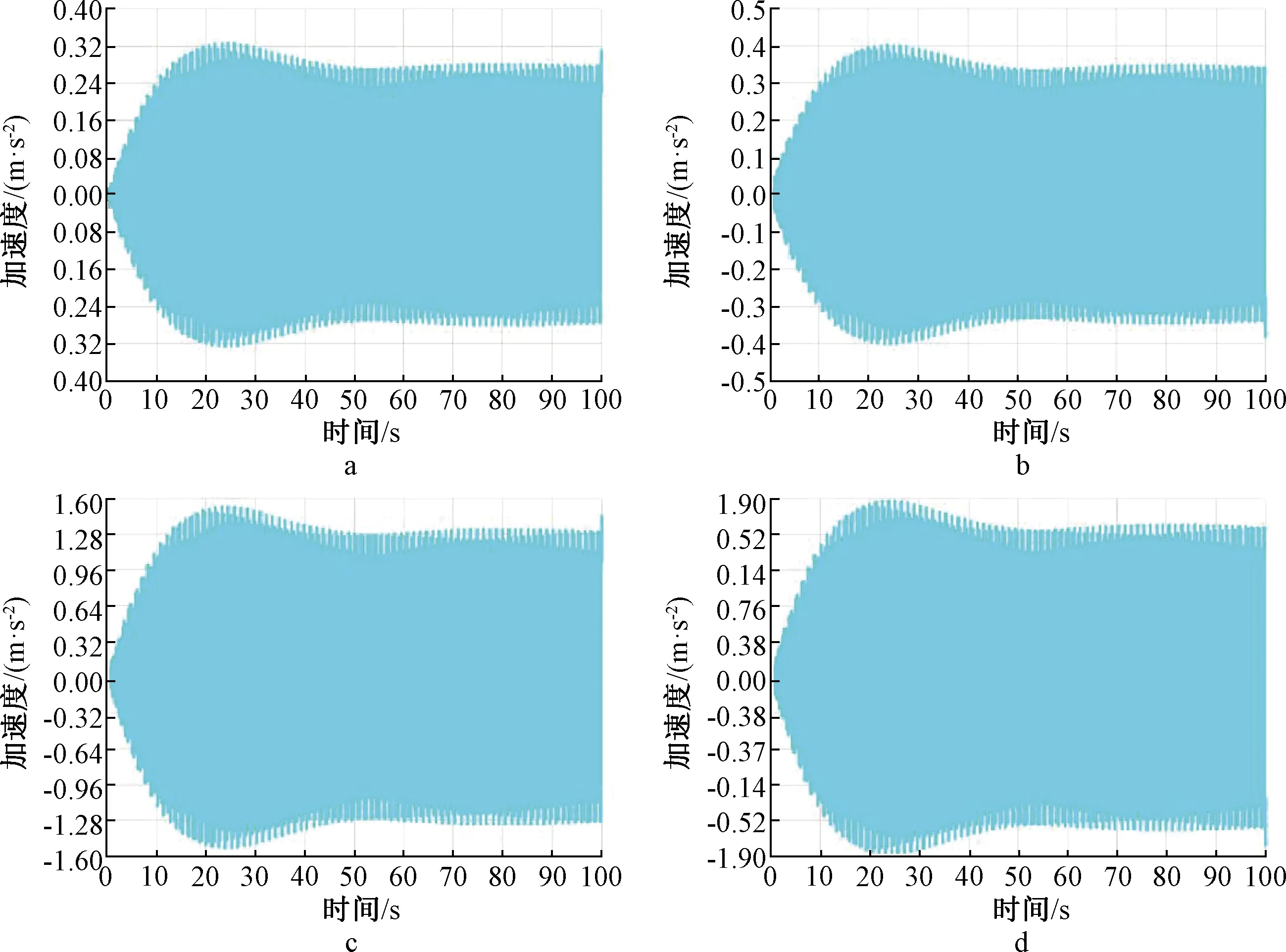
a—工况一时悬挑最大竖向加速度时程； b—工况一时主跨最大竖向加速度时程; c—工况二时悬挑最大竖向加速度时程； d—工况二时主跨最大竖向加速度时程。图16 主跨段和悬挑段在不同工况下的最大竖向加速度时程Fig.16 Maximum vertical acceleration time history of main span and cantilever section under different working conditions

4 振动控制设计

调谐质量阻尼器(TMD)是一种被动减振手段。其减振机理是：TMD系统通过调整频率与阻尼参数，使主振动系统的能量向TMD转移并由其耗散，从而降低主振动系统的振动。但在实际工程应用中发现，TMD的频率调谐很难达到预期效果，于是Xu等提出多重简谐质量阻尼器(简称MTMD)的概念[20]，即由固有频率接近结构频率的多个TMD组成的减振系统，相较于单个TMD，MTMD具有一定宽度的频带，从而频率调谐方面有更好的鲁棒性。

根据本工程的特点，在原设计结构方案的基础上，加装多重调谐质量阻尼器(MTMD)以改变结构阻尼，从而实现控制结构振动的目的，MTMD的具体布置位置如图17所示。

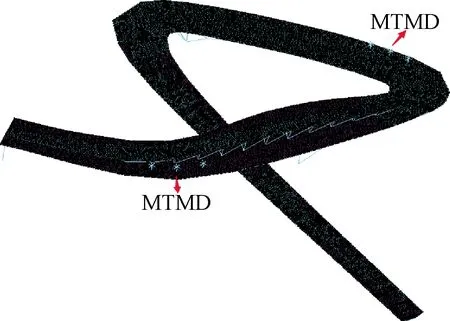
图17 MTMD布置位置Fig.17 Arrangements of MTMD

两套MTMD参数计算如下：每套MTMD的个数为3个，总质量比为2%，频率间隔β=0.2，平均阻尼比ζt=0.028，由此确定各个TMD的自振频率、刚度、阻尼及质量。汇总TMD的设计参数如表7所示。

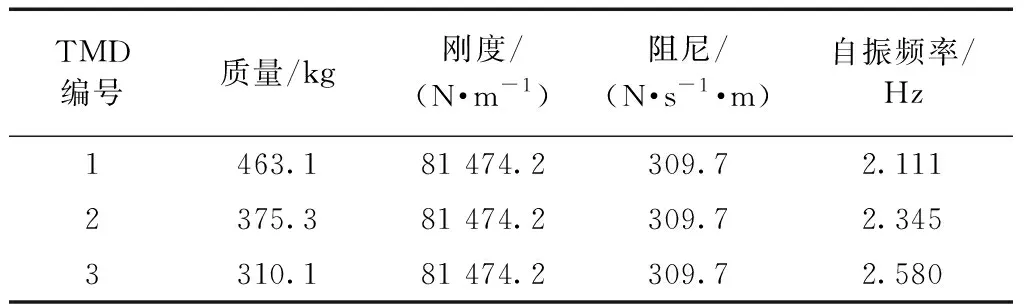
表7 TMD装置的基本设计参数Table 7 Basic design parameters of the TMD device

在原结构主跨及悬挑加速度最大的位置安装MTMD后，得到结构悬挑及主跨的最大竖向加速度响应如图18所示。从计算结果可得：1)工况一，主跨最大竖向加速度为0.073 m/s2，小于加速度限值0.5 m/s2；悬挑最大竖向加速度为0.057 m/s2，小于加速度限值0.5 m/s2，满足舒适性要求。2)工况二，主跨最大竖向加速度为0.340 m/s2，下降82.0%，小于加速度限值1.0 m/s2；悬挑最大竖向加速度为0.268 m/s2，下降82.6%，小于加速度限值1.0 m/s2，同样满足舒适性要求。

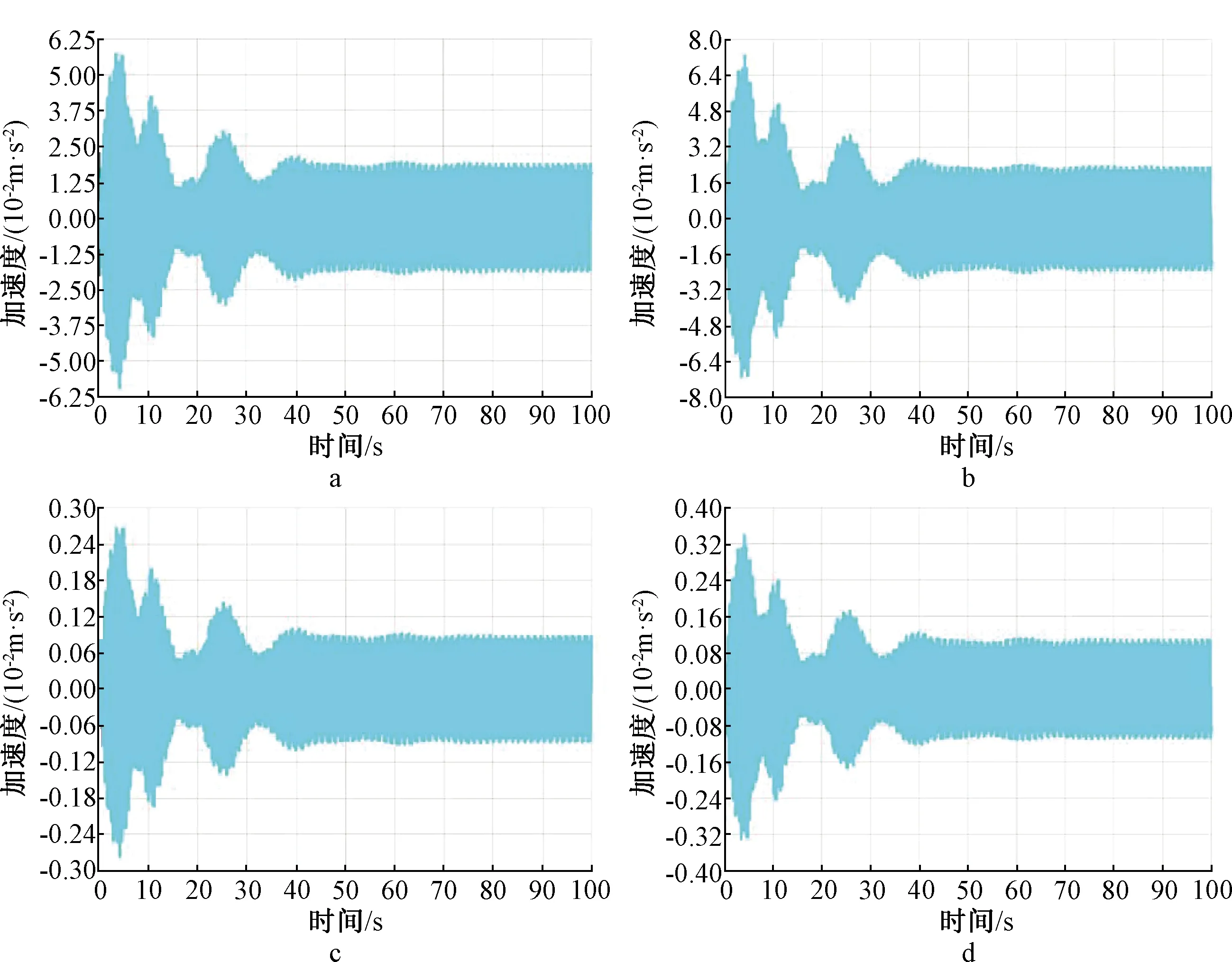
a—工况一时悬挑最大竖向加速度时程； b—工况一时主跨最大竖向加速度时程；c—工况二时悬挑最大竖向加速度时程； d—工况二时主跨最大竖向加速度时程。图18 增设MTMD后主跨段和悬挑段在不同工况下的最大竖向加速度时程Fig.18 Maximum vertical acceleration time history of main span and cantilever section under different working conditions after adding MTMD

5 结束语

1)珠海市情侣路香炉湾大跨度曲线人行天桥通过采用钢-混凝土组合结构形式，特别是在主跨和悬挑段的主梁部分采用钢箱梁-钢桁架复合结构，有效提高了结构刚度、减轻了结构自重、降低了结构高度、提升了人行桥的跨越能力。实例分析结果表明，钢-混凝土组合结构为城市大跨度曲线复杂人行天桥提供了有效的解决方案。

2)大跨度曲线人行天桥振动舒适度设计方面，仅考虑竖向自振频率限值作为唯一评价指标的方法过于简单保守、较难适用，宜采用多种步行激励荷载工况进行全面深入的计算分析，并将人行天桥的人致竖向及侧向振动加速度等舒适度指标纳入综合考虑。

3)合理设置调谐质量阻尼器能够有效控制大跨度曲线人行天桥的人致振动，本文案例中，在人行天桥主跨及悬挑部分加速度响应值最大处各设置一组多重调谐质量阻尼器(MTMD)，可使结构加速度响应峰值分别下降82.0%、82.6%。