基于贝叶斯优化的LSTM高速交通流量预测

沈 括，朱怡帆，孟祥毅，李海济

（安徽大学互联网学院，合肥 230031）

0 引言

由于城市可利用土地不断减少，而机动车流量持续增加，城市的交通系统建设速度无法满足日益增长的交通需求，交通拥堵的情况日益常态化。百度地图公布数据显示，2020 年中国交通拥堵排名前三的城市分别是重庆、贵阳和北京，长期的交通拥堵不仅增大了交通管理难度，还容易发生交通事故。如何缓解交通拥堵、提高通行效率是如今智慧交通面临的重要课题。

在现如今的大数据时代背景下，交通数据的规模不断增大，累积的数据颠覆了传统数据的规模，甚至可以达到PB 级别。基于传统统计模型的数学方法已很难处理这些海量数据，而利用大数据平台所提供的强存储和强计算能力，结合一些神经网络模型、机器学习算法等，可以较好地对大规模交通流量进行预测。

早期的交通流量预测模型，如整合移动平均自回归法（ARIMA）、支持向量机（SVM）、马尔科夫链模型（Markov chain model）等，虽然取得了不错的预测效果，但无法深入挖掘数据之间的内在联系。长短期记忆神经网络LSTM 可以挖掘大数据之间的深层关系，而且能满足神经网络需要大量数据训练的特征，因此该模型在交通、电力等领域的预测中应用广泛，并呈现出良好的长期与短期预测性能。

目前，国内外很多学者对LSTM 模型及应用领域都开展了广泛的研究。瑞典首都斯德哥尔摩、东京、纽约等一些国际性大都市，近些年来也一直致力于交通信息系统解决交通拥堵问题。Altché 和Fortelle在第20 届智能运输系统国际会议上提出利用LSTM 模型预测车辆行驶轨迹。Santosh 等使用大数据技术结合LSTM 模型预测疟疾发病率。国内，程肇兰等基于LSTM研究铁路货运量预测。本文在LSTM 基本模型基础上，构建了基于贝叶斯优化的LSTM 模型，探究交通流量预测，并验证模型的有效性与准确性。

1 基础理论简介

1.1 LSTM神经网络

LSTM是一种在RNN的基础上提出的特殊循环神经网络。相较于传统的循环神经网络，LSTM 可以很好地解决梯度消失和梯度爆炸的问题。其核心之处在于设计一个记忆细胞，具备选择记忆的功能，可以选择记忆重要信息，过滤掉噪声信息，减轻记忆负担。LSTM 使用遗忘门、输入门、输出门来控制信息，完成该网络功能的实现。图1给出了LSTM的工作原理。

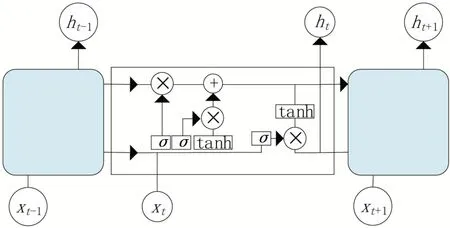
图1 LSTM工作原理

（1）遗忘门。遗忘门的作用是选择性保留细胞中的信息并舍弃价值低的信息，其计算公式为：

W为遗忘门的权重矩阵，h为上一时刻输出向量，x为当前输入向量，b为偏置项，为激活函数。

（2）输入门。输入门的作用是将重要的信息选择性地记录到细胞中，根据细胞状态决定当前时刻的输入，其计算公式为：

W为输入门的权重矩阵，x为当前输入向量，h为上一个时刻输出向量，b、b为偏置项，、tanh为激活函数，f为遗忘门的输出，i是要保留下来的新信息，͂是新数据形成的控制参数，最终实现状态的更新。

（3）输出门。输出门的作用是基于细胞状态决定最终输出结果。其计算公式为：

W为输出门的权重矩阵，b为偏置项，最终得到h可以作为LSTM 的输出值和下一个状态的输入值。

1.2 贝叶斯优化算法

普通求函数极值的问题，可以利用基于梯度的优化来解决。但在LSTM 模型调参的过程中，不能够直接确定对应的函数关系，所以无法使用传统的优化算法来对超参数进行调优。而贝叶斯优化算法是一种black box 优化算法，不需要知道目标函数的表达式，以极其简洁的框架来寻找全局最优解，非常适用于LSTM 模型的调参。

算法的思路是利用目标函数的先验概率分布及已知观测点来更新后验概率分布，然后根据后验概率分布寻找下一个极小值点，使极小值不断减小，最终得到最优超参数。定义贝叶斯优化目标为：

式中是最终优化的超参数，( )是待优化的目标函数。

式中Σ(,)是协方差矩阵：

由贝叶斯定理可知：

通过不断的迭代更新使= x,最终得到最优化的超参数。

算法流程如下：

表示模型未知的目标函数，即所谓的black box；表示所要优化超参数的搜索空间；表示数据集；表示采集函数；表示高斯模型。

1.3 评价指标

本文采用均方根误差和平均绝对误差指标来对不同模型的预测结果进行评估。

（1）均方根误差（RMSE）

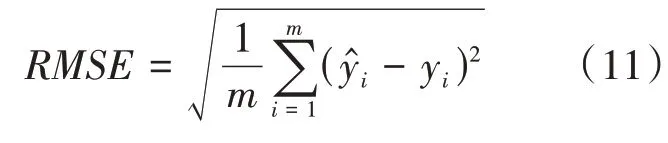
均方根误差指预测值与实际值偏差平方的平均值再取平方根，用来衡量预测值和实际值之间的偏差。

（2）平均绝对误差（MAE）

平均绝对误差指各次预测值与实际值的绝对偏差的平均值，可以避免误差相互抵消的情况。

2 基于贝叶斯优化的LSTM模型

在传统的LSTM 神经网络训练过程中，需要人为调节超参数。超参数的取值对模型的性能有很大的影响，但超参数的选择无规律性，且具有很大的偶然性，这对人为调参很不友好，往往无法得到最优超参数。针对这一问题，本文引入贝叶斯优化算法，贝叶斯优化算法主要包含概率代理模型和采集函数两个部分。概率代理模型可以利用高斯过程寻找目标函数的近似，得到目标函数的后验概率分布；采集函数根据后验概率分布，在未知区域和已观测到出现最优结果的区域进行采样，选择合适的样本点使得目标函数取极值。综上分析，本文引入基于贝叶斯优化的LSTM模型。

该模型分为三个阶段，第一阶段训练LSTM模型，第二阶段将需要进行优化的超参数传入贝叶斯优化模型，第三阶段利用优化后的LSTM模型输出预测结果。图2给出了基于贝叶斯优化的LSTM模型流程。

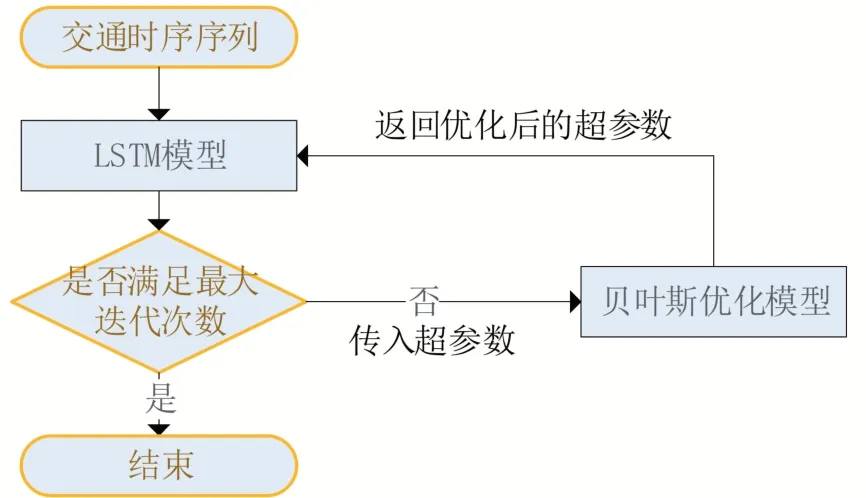
图2 基于贝叶斯优化的LSTM模型流程

（1）LSTM训练阶段

步骤1 超参数初始化。

步骤2 输入训练集进行LSTM 神经网络的训练。

步骤3 输出与训练集维度一致的数据，并不断地对超参数进行更新。

（2）贝叶斯优化阶段

步骤1 定义需要优化的超参数，并设置参数空间。

步骤2 定义优化目标函数，并将定义的超参数带入LSTM模型进行训练。

步骤3 利用高斯过程求目标函数的后验概率分布，根据后验概率分布对超

参数样本点进行采样，优先选择最优超参数，实现对超参数的更新。

步骤4 不断更新目标函数的后验概率分布和超参数，直至满足模型的要求。

（3）LSTM预测阶段

步骤1 将验证集传入训练好的LSTM模型，输出预测结果。

步骤2 根据预测结果求出误差。

3 实例分析

3.1 数据来源

本文使用的数据集是2018 年英国高速公路数据集，该数据集以十五分钟为周期，连续观测高速公路的流量。其基本信息如表1所示。

表1 数据集的基本特征

3.2 数据的预处理

（1）原数据集主要包含时间、不同种类车流量和速度等信息，但存在某些缺失值和异常值，需要对数据集进行清洗，去除缺失值和异常值。

（2）根据原数据集的不同种类的车流量计算某一时刻的总车流量。

（3）对数据进行归一化处理（按最大最小值中心化，再按极差缩放），去除量纲影响。

（4）将前90%的数据集作为训练集，后10%的数据集作为验证集。

3.3 模型对比

本文使用keras 框架来进行神经网络模型的训练，引入序贯模型来描述各层网络。为了进一步探究贝叶斯优化的LSTM 模型处理时序序列的优越性，本文建立了RNN 神经网络模型、GRU神经网络模型与其进行对比。

3.3.1 RNN神经网络模型

RNN 是指随时间推移重复发生的结构，一般适用于处理序列数据。RNN 记忆模块可以获取计算过的信息，具体表现为对上一时刻的信息进行记忆并应用到当前时刻的输出。其最大的特点是循环利用不同时刻的信息，但隐含层的输入会随着时间的推移覆盖原有信息，造成梯度消失问题。

3.3.2 GRU神经网络模型

与LSTM相似，GRU的设计也是为了解决长期记忆依赖中的梯度消失和梯度爆炸等问题。相较于LSTM复杂的重复网络模块，GRU只有更新门与重置门，结构大大简化的同时也保持了较好的效果。更新门的作用是决定更新的效果，控制上一时刻的特定信息保存到当前时刻，重置门的作用是控制上一时刻的特定信息被忽略。通过两个门函数，GRU 最终将重要信息保存下来。

4 实验结果与分析

4.1 实验结果

图3给出了不同模型在验证集上的预测效果，表2 给出了不同模型预测结果的误差指标，可以看出贝叶斯优化的LSTM 模型预测的结果最优。

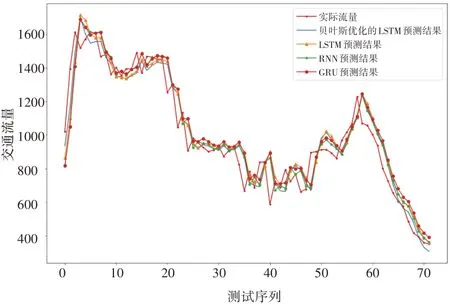
图3 各模型流量预测结果

根据表2 的结果可知，贝叶斯优化的LSTM模型预测结果的RMSE、MAE 分别为95.683、75.373。相较于LSTM 模型，均方根误差降低了6.30%，平均绝对误差降低了5.67%；相较于RNN 模型，均方根误差降低了10.10%，平均绝对误差降低了7.44%；相较于GRU 模型，均方根误差降低了16.12%，平均绝对误差降低了13.20%。可以看出贝叶斯优化的LSTM模型预测结果更接近真实值，精度更高。

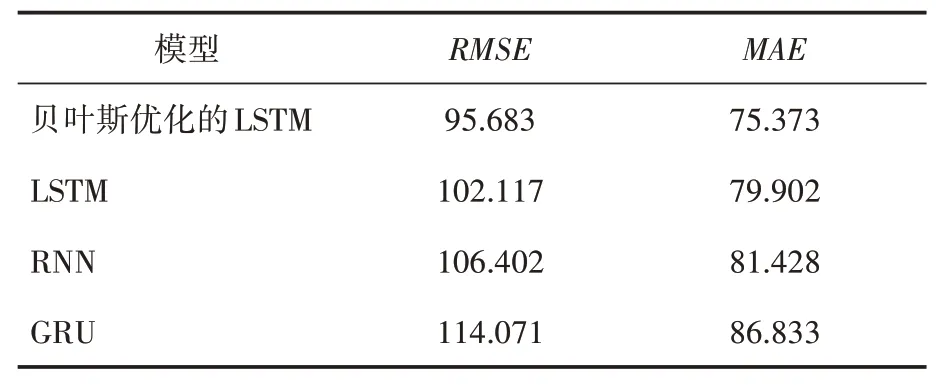
表2 对高速公路时间序列预测结果

4.2 误差分析图

图4给出了不同模型的误差对比柱状图，图中的柱状图越高则说明误差越大。从图4可以看出，GRU 模型的RMSE 和MAE 对应的柱状图最高，贝叶斯优化的LSTM 模型的RMSE 和MAE对应的柱状图最低，说明贝叶斯优化的LSTM 模型误差最小，相较于其他模型优势明显。

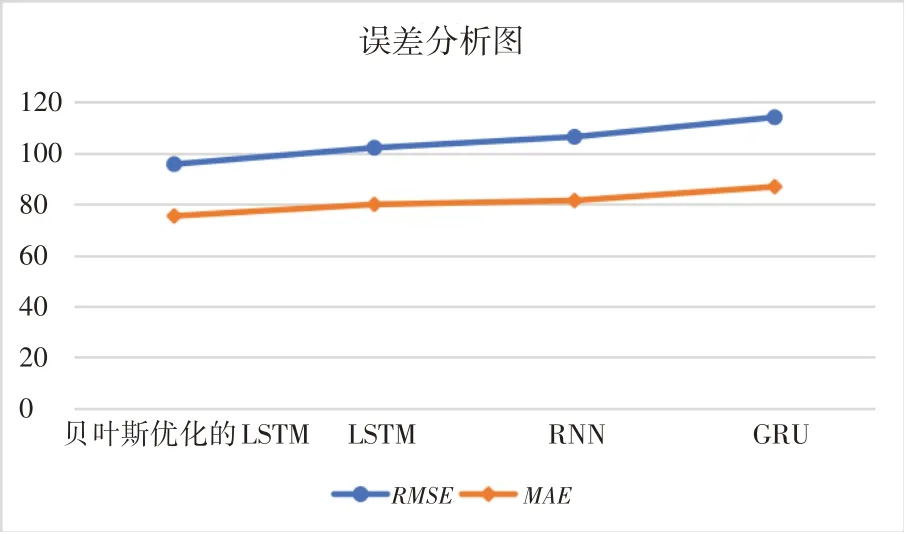
图4 不同模型的误差分析

5 结语

本文提出了基于贝叶斯优化的LSTM 模型，用于探究高速交通流量预测问题。首先对模型的基本理论进行了分析，然后引入贝叶斯优化的LSTM 模型，最后进行实例分析来验证模型的优越性。通过实验结果可以看出，基于贝叶斯优化的LSTM 模型预测精度高于其它模型，能够准确地预测高速交通流量，具有一定的应用价值。在高速交通流量预测过程中，影响因素复杂多变，探究多因素模型对预测精度的影响将是下一步的研究方向。