浅论如何提升高等代数教学效果
周瑞铭 张会平
1.中央民族大学理学院 北京 100081;2.中国人民大学数学学院 北京 100872
高等代数课程是数学、物理、计算机、金融工程等学科的一门重要学科基础课和必修课,其内容深广、抽象程度高[1-9]。在高等代数教学中,抽象的概念、烦琐的论证与复杂的计算相交织,这使得许多知识点的讲解存在一定难度,学生们也不容易提起学习兴趣,教学较难达到好的效果。在教学过程中有没有适合这门课程特点的、有效的方法来促进学生的学习、提升教学效果?笔者在教与学的实践中体会到几个有效的方法,与读者共享。
一、让抽象的概念“接地气”
在高等代数这门课程的学习过程中,接触每个知识模块之初都会接触到一些抽象概念,学生对这些概念的理解直接影响到他们的学习自信心以及对整个课程的学习效果。因此,如何设计教学方案并付诸实施,使得学生能够顺利理解并内化这些概念就尤为重要。在教学实践中,我们发现用一些学生们能够看得见摸得着的例子做引导,教学效果明显提高。
我们来看一个例子。现代代数学是研究“结构与关系”的学科,教师在讲授并培养学生这一观念的时候,许多同学对结构与关系这两个抽象的概念不能理解。在教学中尝试把这些概念代入学生的具体生活中,使抽象的概念“接地气”,教学效果明显提升。比如在本例中,教师先提出问题:“教室里就座的所有人是否构成一个非空集合?”学生们很容易理解并给出肯定答案。
其次,教师引导学生们建立这样的意识:如果教室中所有人相互之间都不认识,都不打交道,那么这个集合就仅仅是一个“人的集合”,没有活力。
最后,教师提出假设:如果在教室里的人与人之间建立一种“互动”的方式,互相产生联系(注意提醒学生这种联系的方式需要遵守一定的规则,比如要文明有礼不能打人骂人),紧接着提出问题引导学生思考:请问这个时候这个教室里的所有人构成的集合与刚才没有“互动”的集合有没有区别?学生思考后可以发现,“有互动”的这群人的集合和“无互动”的人的集合是不同的。此时,教师板书或PPT演示如下内容:

这样学生们很快就能理解代数中“结构”这个观念的核心与本质:即“结构”是一个配备着运算的集合(当然,这个或这些运算需要遵守一定的规则)。
以上例子取自于由学生们自己构成的集合,学生们有参与感、很容易产生兴趣,而且该例子也易于理解,从而教学效果良好,使学生们初步建立了“结构观”这一重要理念。
此时教师趁热打铁,再以实数域R上的n维向量集合Rn为例,指出这是一个非空集合,该集合上有向量之间的加法运算,以及R中的数与Rn中向量之间的数乘运算,且这两种运算满足一系列的性质,这样的配备着加法与数乘运算的集合Rn就是一个代数结构,称之为实数域上的n维向量空间。通过此例,学生对“结构”观念的理解进一步加深,且对课程所学习的具体内容n维向量空间Rn有了更深一层次的观照,抽象思维能力得到训练与提升。
二、把烦琐的叙述形式“变简单”
高等代数中许多问题的叙述或论证过程在形式上十分烦琐复杂,这往往使学生们望而生畏,裹足不前。在教学中针对这些情况,教师不同的处理方式造成的教学效果差异很大。教师如果在合适的地方简化形式表达,把烦琐的叙述变简单,或者依托具体的例子来讲解问题的本质,可以使学生的注意力从复杂的数学公式表达和烦琐的语言叙述转到问题的核心,教学效果会有大幅提升。
例如,“矩阵的秩”是矩阵、向量、线性方程组等研究对象的连接点,是教学中的重点,其中矩阵秩的定义与矩阵的行秩和列秩的关系是教学中的一个难点[1-5],尤其在证明“矩阵的秩=矩阵的列秩”的时候,教材中的证明过程叙述烦琐,造成学生看不到问题的核心和学习上的困难。对于这个情况,教师在课堂上如果采用简单的例子来展示思维过程,比如选取低阶矩阵为例来证明该结果,简化形式,在学生可以够得着的地方做引导,学生会觉得这个困难的内容并不是高不可攀,从而理解证明的思路并进一步顺利解决更广泛的情形下的类似问题。
又如初等矩阵在矩阵论中是一个重要的研究对象,它完全确定了初等变换前后两个矩阵的关系,同时在求逆矩阵及求二次型的标准形中起着核心作用,因此,对初等矩阵性质的研究就尤为关键。但是在说明“初等矩阵左乘或右乘一个矩阵的结果是什么”的时候,如果证明一般n×n矩阵的结果,论证过程的叙述形式就十分烦琐,学生的注意力很容易放在这些“令人头大”的高阶矩阵表示上,从而对问题本质的关注不够、理解不透彻。这个时候,教师选取几个低阶具体矩阵作为例子演示,并引导学生自己举几个具体例子算一算,那么教学的效果将事半功倍。
类似的,对于线性方程组理论中齐次线性方程组基础解系的求法、线性方程组求解的矩阵消元法等内容,如果直接讲解多元线性方程组理论,则问题的叙述及解决过程冗长,学生抓不住重点。在这种情况下,教师若精心选取几类具体的、有代表性的三元或四元线性方程组分类演示解决问题的过程,则学生得以窥见复杂形式下的核心理论与方法。
三、从“看热闹”到“摸门道”
在高等代数学习过程中,有些定理的证明由于篇幅过长或涉及的知识模块较多显得十分困难。对于这些问题,如果教师引导学生把它们当作“名画”或“名曲”来慢慢欣赏、细细品味,那么学生也将可能在轻松愉快的心情中获得知识与美的感受,建立起对数学的学习兴趣,继而从“看热闹”逐步过渡到“摸门道”,数学素养不断提高,教学效果显著提升。
怎样才能让学生看出门道?这主要在于教师要重视展示思维的过程。以处理比较困难的或比较大的知识体系为例,一个有效的办法是先把整个内容拆解为几个模块,容易理解的模块只说明这一模块在整个体系中的地位与作用,涉及的详细证明过程教师略讲或不讲,以培养学生们独立解决问题的能力和建立自信心;难以理解的模块教师细细讲、慢慢讲,并在学生提出问题的地方反复多次多角度分析讨论;而知识体系中的核心部分更需要精讲,尤其要点明该模块在整个理论体系中的作用与地位。
以处理伴随矩阵这一知识点为例,把整个知识点的学习分成五个模块:准备、概念引入、性质、地位与作用、补充说明。下面我们详细说明具体处理的过程。
首先,在准备阶段教师指导学生复习代数余子式以及行列式理论中的一个常用结果:
对于n×n矩阵A=(aij)n×n,有:
其中|A|是该矩阵的行列式,Aij是aij的代数余子式。
做好这些准备后,第二步给出伴随矩阵的定义,伴随矩阵的定义比较简单,只需要提醒学生牢记伴随矩阵中代数余子式的位置。接下来第三步给出伴随矩阵的基本性质:对于n阶方阵A,有:
AA*=A*A=|A|E
这一性质的证明并不困难,教师引导学生尝试独立运用前面的准备知识进行证明,教师不需要讲解,这样可以让学生更好地记住该结论,也有助于培养学生的学习信心。
接下来,教师指出重点,明确告诉学生现在进入该知识点的关键部分,引导学生思考引入伴随矩阵的作用是什么?然后证明以下定理:
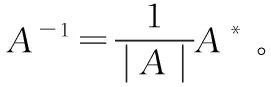
这个定理的结论非常重要,为了加深印象,教师在此处需要带领学生一起进行证明。同时更重要的是指出该定理的作用:该定理给出了用行列式的值是否为零来判别矩阵是否可逆的方法。教师在此处需要明确多次反复强调这一点,并指出用该办法判断一个具体的方阵是否可逆非常有效。进一步,教师需要点明课程中引入伴随矩阵这一知识点的最主要作用也是为了得到该定理,即在课程中,伴随矩阵是可逆矩阵这一知识模块的一个附属工具。
利用该定理还能够得到一个非常重要的推论。
推论:对于n阶方阵A,如果存在矩阵B使得AB=E(或BA=E),则A可逆。
这个推论的结果与可逆矩阵的定义相比较,显然用该结论判断方阵是否可逆比用定义要简单,因此在实际应用中,对于判断非具体的方阵是否可逆常用的是该推论。教师在此处需要再次强调伴随矩阵的出现是为了证明以上定理及其推论,它们都是判断方阵是否可逆的重要且简单的办法。
最后补充说明:对于定理中的另一个结果,即用伴随矩阵求逆矩阵是不是求逆矩阵的有效办法?教师需要举两个具体的例子给学生独立计算,这样做的益处是,学生在做题的过程中自己就能够感受到用该办法求逆矩阵的计算量大出错率高,从而他们可以体悟到对于一个具体的可逆矩阵,利用伴随矩阵来求其逆矩阵的可行性不高。
从上面的例子我们可以感受到教师把握了整个教学节奏,学习内容的处理详略得当;教学中学生有实践、有思考、有体会,清楚了为什么引入伴随矩阵、伴随矩阵的地位与作用,更重要的是学生深刻理解并能应用核心结果:即用行列式的值来判断矩阵是否可逆。这样的教学过程让学生们逐步感受到了数学中层层相扣的逻辑美,感受到了跌宕起伏的节奏美,感受到了全面分析问题的结构美,摸到了学习的“门道”。
结语
以上几点是笔者在高等代数教与学过程中的几点小的体悟。高等代数是一门常学常新、常教常新的课程,如何提高学生的学习兴趣和提升教学的效果,还需要不断地探索与学习。希望本文起到一个抛砖引玉的作用,期待与读者朋友共同探讨、交流沟通。

