基于机构随机振动分析的载荷谱非参数上限统计归纳方法对比研究
冯志杰,肖慧婷,杨永锋
1.航空工业航宇救生装备有限公司航空防护救生技术航空科技重点实验室,湖北 襄阳 441000
2.西北工业大学,陕西 西安 710072
机构在使用过程中会受到各种因素的影响,其中振动环境会影响机构关键部件的使用寿命,甚至影响整个机构的安全性及可靠性。而载荷谱作为机构关键部件疲劳寿命及环境可靠性研究的重要组成部分,能否对其进行正确的数据处理与编制,对于保障整个机构的安全性及可靠性具有十分重要的意义。
李雷[1]等建立了某型弹射座椅的有限元计算模型,提出了飞机弹射座椅振动响应的有限元计算方法。基于该方法,冯志杰[2]等对某型飞机弹射座椅椅载设备进行了随机振动仿真研究,获取了椅载设备两个不同测点处的振动载荷谱,并对其进行数据归纳。当选取少量测点对振动数据进行归纳时,出现偶然误差的概率较大,可能导致得到的载荷谱过考核或欠考核,因此需对部件多个测点响应进行归纳分析。丰志强[3]等针对飞机机载设备在振动环境可靠性试验剖面的编制需要,依据标准对机载设备振动试验数据进行了归纳。田永卫[4]等对某型飞机多个舱位和主要结构部位进行了振动量值的飞行实测,并对多个不同测点的试验数据采用参数归纳法进行了数据处理。依据GJB 150A的准则,参数归纳法仅适用于总体近似服从正态分布的数据集[5],但由于测点位置的选取可能会影响响应数据集概率分布情况,因此当测得的数据集总体不完全服从正态分布时,参数归纳法便不再适用,应采用非参数归纳法处理不同测点数据。
本文对于机构部件载荷谱获取方法进行了研究,首先对机构进行随机振动分析,然后提取机构关键部件上不同测点的响应数据,再通过非参数上限统计归纳方法处理响应数据。基于有效性和无偏性分析,评价了不同归纳方法的载荷谱归纳结果,最终得出较优的机构关键部件载荷谱归纳结果,为后续关于部件的可靠性及寿命的研究提供帮助。
1 机构部件动力学响应获取方法研究
若直接将机构安装位置载荷谱作为关键部件安装位置处的载荷谱对部件进行动力学研究[6-7],则不能考虑从激励输入点到关键部件之间的传力路径,因此提出更符合实际的机构关键部件载荷谱获取方法[8-12]。
将机构安装位置处的载荷谱作为机构载荷谱,对机构进行随机振动仿真分析,提取关键部件安装位置附近不同测点处的响应,对不同测点处的响应进行归纳包络,将归纳后的曲线作为关键部件的载荷谱,以探究关键部件在振动环境下的动力学响应及寿命等。机构关键部件载荷谱获取过程如图1所示。
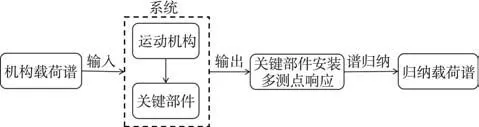
图1 机构关键部件载荷谱获取流程Fig.1 Load spectrum acquisition process of key components of mechanism
随机振动的计算过程包括两个阶段[13]:(1)计算系统响应特性,在时域内用脉冲响应函数h(t)表示,在频域内用复频响函数H(ω)描述,其物理意义为系统响应与激励之比;(2)通过系统响应特性和随机激励计算功率谱密度矩阵Sxx(ω)。
通过随机振动分析得到关键部件不同测点的响应后,对结果进行归纳。以往在对机构关键部件响应数据进行处理时,直接用仿真或实测的某一个点或某两个点的包络作为关键部件的载荷谱[1-2]。取点数目较少时,得到的部件载荷谱不够准确,因此需对关键部件多个测点响应进行归纳研究。
2 振动数据归纳方法研究
GJB 150A 的18A[5]中规定了5 种数据集上限的统计分析方法,包含两种参数上限统计估计方法和三种非参数上限统计估计方法。两种参数上限统计估计方法分别是正态单边容差上限法(NTL)和正态预测上限法(NPL);三种非参数上限统计估计方法分别是包络上限法(ENV)、无验前分布容差上限法(DFL)和经验容差上限法(ETL)。参数上限统计法适用于满足正态分布或者经转化后满足正态分布的数据集,而非参数上限统计法适用于不满足正态分布或者转化后不满足正态分布的数据集。在对部件不同测点响应进行数据归纳时,测点位置的选取会影响数据集分布,因此采用非参数上限统计方法归纳部件不同测点数据集。
2.1 ENV法
ENV 法的计算方法为选取数据集中最大估计值作为最大上限,以谱曲线一个频段上的谱线作为研究对象,所有样本在该段谱线上的容差上限为

式中:N表示数据集的样本容量,xi表示第i个样本的谱线值。
该方法计算简单,忽略了样本的分布特性,无法给出超过该值的概率。当估计集有异常的情况下,包络上限法可能过于保守,对于谱线带宽也很敏感。
2.2 DFL法
DFL法计算方法同ENV法一致,取数据集的最大值作为上限估计值,但不同于ENV 法的是,DFL 法引入了置信度和覆盖率。
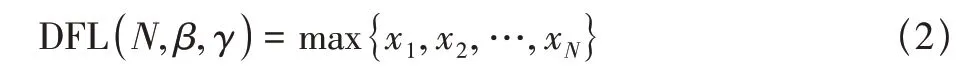
式中:β表示覆盖率,γ表示置信度。用xβ代表数据集样本的真实上限,则数据集样本小于xβ的概率为β,即

若要使样本中的最大值xmax小于xβ,则数据集中每一个样本都应小于xβ。每个样本之间相互独立,故有
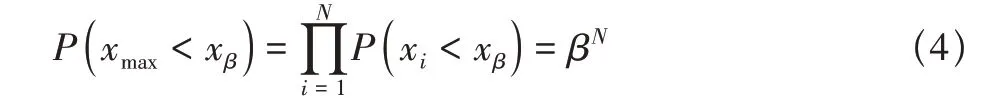
xmax≥xβ的概率为
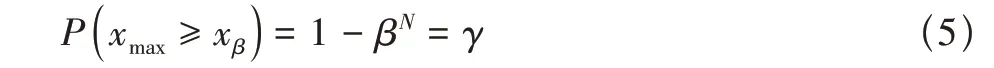
工程中通常使用的置信度至少为50%,覆盖率为95%[11]。若要使估计上限置信度γ≥50%且β= 95%,由式(5)计算得N≥14;若要保持置信度大小不变,取覆盖率较大时(β>0.95),计算所需的样本数量较大。
2.3 ETL法
经验容差上限一般表示为ETL(β)。假设共有N个测量点,每个测量点的输出响应谱曲线有M段谱线,则总数据集中共包含NM个样本

式中:j= 1,2,…,M,i= 1,2,…,N,mj表示第j段谱线的样本均值。在M段谱线上构造的正则化估计集为
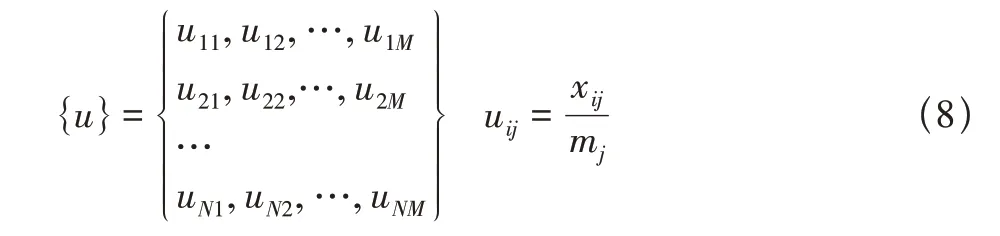
将正则化估计集{u}中所有数据按从升序排列,数据集中第k个元素以u(k)来表示。构造{u}的经验分布函数FN

取覆盖率为β时,有

采用经验分布函数FN代替实际分布函数F,取覆盖率为β,由式(9)计算得k值,用u(k)作为容差上限uβ的估计值。每段谱线上的经验容差上限为
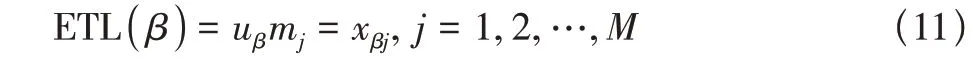
取置信度为50%,此时xβj表示在第j段谱线上,EBL(β)以50%的置信度超过所有值的100β%。若选择大于xβj的值,置信度会增加。当样本容量N达到一定要求时,不同频率分辨率带宽上的正则化估计集应服从同一分布。
ETL法是根据整个频带分布计算各频率段谱线上的容差上限,因此可以消除一些偶然因素带来的误差,可以得到相对稳定的结果,但其样本量通常应大于10[10]。
3 上限估计方法优劣性评价
不同方法归纳得到的载荷谱必然存在优良之分,故需要评价哪个估计方法相对较好。评价标准主要有无偏性评价和有效性评价。(1)无偏性评价:对于真实容差上限θ,其估计量̂满足E=θ,则称估计量̂为真实容差上限θ的无偏估计量。(2)有效性评价:设总体X~F(x;θ),对于真实容差上限θ的两个无偏估计量̂,,如果,则比有效。
本文通过对不同归纳方法得到的载荷谱结果的有效性和无偏性评价,对比分析归纳结果的优良性。取总样本容量为N,将每段谱线样本按样本观测值升序排列,取第95%N个样本作为总体覆盖率为95%的理论上限。基于无偏性和有效性,评价各方法得到的容差上限估计量的优劣性。当各容差上限估计量均值越接近理论上限,方差越小,则说明该方法估计得到的载荷谱越接近真实工况。
4 实例分析
以某型弹射座椅为例,通过有限元分析获得仿真结果,将椅载关键设备安装位置不同测点处的响应结果进行载荷谱归纳。能准确获得人椅系统弹射座舱的各种参数是提高救生性能的关键[12],但在紧急状况下弹射座椅帮助飞行员顺利出舱的首要前提是保证弹射座椅关键设备在飞机正常飞行过程中的安全性和可靠性。采用程序控制器作为弹射座椅关键部件,讨论不同数据归纳方法得到的载荷谱归纳结果的优良性。
4.1 模型建立及响应计算
以保证主结构完整性、传力路径不变为原则,对某型飞机弹射座椅模型零部件进行简化。该型飞机弹射座椅主要材料为铝合金,其各项材料参数见表1。

表1 材料参数Table 1 Material parameters
座椅激励谱是通过加速度传感器实测得到,再根据GJB 150[5]中相关规定对试验数据归纳处理得到。以某型弹射座椅振动耐久垂向载荷谱为例进行计算分析,载荷曲线如图2所示。
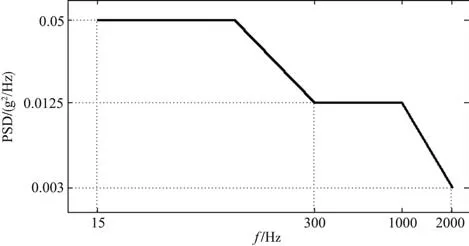
图2 飞机座舱振动耐久垂向加速度载荷谱Fig.2 Aircraft cockpit vibration endurance vertical acceleration load spectrum
完成有限元模型处理后,先对模型进行频率响应分析获取频响函数,再对其进行随机响应分析,获取测点处振动响应。在程序控制器安装位置附近各取900个节点作为响应输出测点,座椅简化模型及程序控制器安装位置如图3所示。

图3 弹射座椅简化模型及程控器安装位置Fig.3 Ejection seat simplified model and installation position of program controller
4.2 正态性检验
当谱密度曲线样本的每个频率分辨率带宽数据集服从正态分布时,加速度均方根值(RMS)也近似服从正态分布[10]。各测试点的加速度RMS值可由式(12)计算
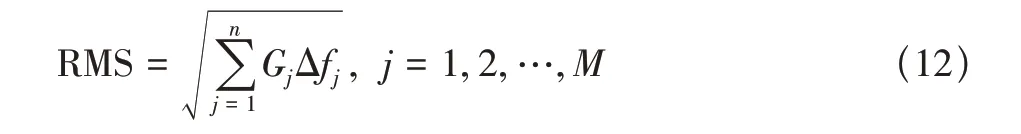
式中:Gj和Δfj分别为第j个谱线上的谱密度和频率带宽。
加速度RMS值的分布特性可以反映信号的采样点数、平均值和方差,因此可以通过对不同测点RMS值的分布研究谱密度曲线样本是否服从正态分布。分别绘制程控器安装位置不同测点处振动响应的加速度均方根值Q-Q 图和直方图,如图4和图5所示。

图4 程控器各测加速度点RMS值Q-Q图Fig.4 Quantile-Quantile diagram of RMS value of each accel eration point measured by the program controller

图5 程控器各测点加速度RMS值直方图Fig.5 Histogram of acceleration RMS value of each measuring point of the program controlle
通过程控器安装位置附近不同测点处的加速度RMS值Q-Q图和直方图,可判断该谱密度曲线集不完全满足正态分布,因此需对其进行非参数上限统计归纳。
4.3 归纳结果
对于ENV、DFL 法,计算方法较为简单,按照第2 节所述连接各段谱线上最大值,最终得到载荷归纳谱;ETL方法需将各个测试点的所有频段上的谱线数据提取出来作为估计集,依据式(6)将所有样本值进行正则化,得到正则化估计集,对该正则化估计集取覆盖率为β= 95%,利用式(9)~式(11)计算得到每段谱线宽上的经验容差上限值,终得到95%覆盖率下的载荷归纳谱。采用ENV、DFL和ETL方法绘制得到的归纳曲线如图6~图8所示。
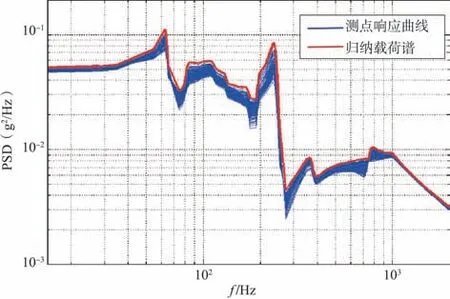
图6 ENV法归纳谱曲线Fig.6 The spectrum curve induced by ENV method
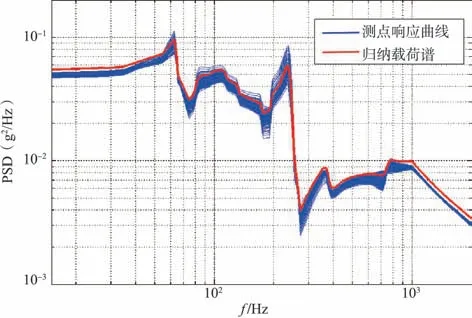
图7 DFL法归纳谱曲线Fig.7 The spectrum curve induced by DFL method

图8 ETL法归纳谱曲线Fig.8 The spectrum curve induced by ETL method
图6和图7中的载荷归纳谱一样,原因是ENV法和DFL法计算容差上限估计值的方法是一样的。两种方法的区别在于DFL法引入了参数置信度和覆盖率,可以通过样本容量和其中一个参数计算另一个参数。在本文后面讨论中将ENV 法和DFL 法归并讨论。对比ENV/DFL 法和ETL 法的归纳结果(见图9)可看出,由于ETL法考虑了整个频率范围内的分布,消除了一部分由取点位置随机性等因素产生的谱线值波动,导致其在峰值点的上限估计值均小于ENV/DFL法峰值点的上限估计值。为了验证计算的准确性,对比参考文献[2]中的试验结果与ETL 法归纳结果(见图10)可看出,试验结果与归纳结果幅值及趋势基本一致。计算得归纳谱加速度RMS=4.8844g,试验测得加速度RMS=5.0893g,计算得误差为4.02%。
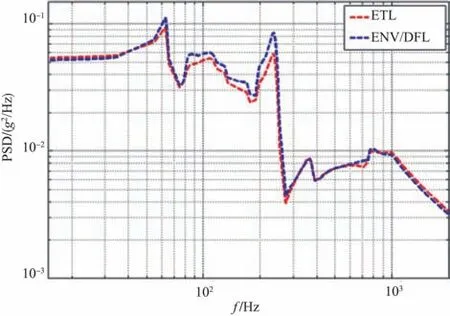
图9 ENV/DFL法和ETL法归纳结果对比Fig.9 Comparison of inductive results between ENV/DFL and ETL

图10 ETL法归纳结果与试验结果对比Fig.10 Comparison between ETL inductive results and experimental results
4.4 归纳结果优劣性评价
对三种方法的归纳结果进行无偏性和有效性评价。取总体样本容量N为900,按升序排列各谱线值,取第855 个数据(95%覆盖率)作为理论上限值。样本容量分别设定为5、13、30、45、60、75 和90,每个容量下重复抽样10 次,计算10次抽样的载荷谱归纳结果的均值和方差。载荷谱线的加速度RMS值能反映信号的平均能量,峰值点的波动大小能反映载荷对机构部件的破坏性强弱,因此取载荷谱线的加速度RMS 值和峰值f= 62.78Hz 处的归纳结果作为讨论对象进行优良性评价。首先分别计算各样本容量10 次抽样归纳结果的均值和方差,然后将计算所得均值除以理论上限进行归一化处理。计算得到的结果见表2~表5,对比不同归纳方法得到的峰值点和加速度RMS 值的归一化均值及方差可以发现:(1)无论是对于峰值点还是加速度RMS值,ENV/DFL 法得到的归纳结果随着样本容量的增加,归一化平均值不断增加,且方差波动幅度较大,无法趋于稳定;(2)ETL 法由于考虑了各测点每段谱线整体分布,其归纳结果消除了一部分波动。所以随样本量增加,其归纳结果的归一化均值变化幅度较小,方差逐渐趋于稳定。

表2 不同抽样次数下各归纳方法在f=62.78Hz 处的归一化上限平均值Table 2 The normalized upper bound mean of each inductive method at f=62.78Hz under different sampling times

表3 不同抽样次数下各归纳方法在f=62.78Hz处的上限值方差((g2/Hz)2⋅10−6)Table 3 The upper bound variance of each inductive method at f=62.78Hz under different sampling times

表4 不同抽样次数下各归纳方法加速度RMS值的归一化上限平均值Table 4 The normalized upper bound mean of each inductive method of acceleration RMS under different sampling times

表5 不同抽样次数下各归纳方法加速度RMS值的上限值方差((g2/Hz)2⋅10−4)Table 5 The upper bound variance of each inductive method of acceleration RMS under different sampling times
综上所述,ETL 方法得到的载荷谱归纳结果的无偏性和有效性均优于ENV/DFL方法得到的归纳结果。
5 结束语
本文建立了一种机构关键部件载荷谱获取方法。首先对机构进行随机振动分析,获取关键部件测点响应,然后对响应数据集进行归纳处理,最终得出部件的载荷谱。通过对比不同归纳方法的理论分析以及实例结果,得出以下结论:当样本容量N≤13时采用ENV/DFL方法得到的估计结果波动较大,故采用ENV/DFL 法时样本量不宜过小;ETL方法相对ENV/DFL方法得到的估计结果更稳定,但当样本量较大时ETL法对于载荷谱波动较小的频段上限估计值较大,而波动较大的峰值附近其上限估计值较小,因此采用ETL法时样本量不宜过大。

