风速对自然通风教室内咳嗽飞沫液滴扩散的影响

曾凯磊 陈燕 谭堰琴 朱清源

东华大学环境科学与工程学院

室内环境中的呼吸道传染病一直是困扰人们的公共卫生问题，比较典型的呼吸道传染病有——从发现之日起一直与人类共存的流感和肺结核，曾造成巨大危害但逐步被消灭的SARS 以及2019 年年末爆发的至今仍在世界各地蔓延肆虐的新型冠状肺炎疫情。呼吸道传染病的病原体主要以人体呼出的飞沫为载体实现人群之间的传播，而人体飞沫在室内的传播输运特性受唾液滴的释放位置，释放速度，粒径大小以及室内通风方式的影响[1-3]，Chen 等[4]人在分析了影响飞沫液滴扩散的众多因素后指出室内通风方式和初始呼气速度的影响占主导地位。当前所进行的飞沫液滴等颗粒污染物的扩散研究大多基于机械通风背景，而机械通风背景下的飞沫等颗粒污染物的扩散分析并不一定都适用于自然通风，因此有必要对自然通风背景下的飞沫液滴进行扩散分析。学校教室内人员相对密集，且大多数不具备机械通风条件，本文以自然通风教室为背景，数值分析教室进风风速对人员咳嗽飞沫液滴颗粒扩散的影响。

1 物理数学模型

1.1 物理模型

原型为东华大学第一教学楼1107 教室，桌椅为组合式桌椅，未固定可灵活摆放，具体的摆放方式为9排5 列。根据实地测量结果对教室及教室内桌椅、门窗进行尺寸取整，桌椅均简化为实体方块，人体模型则参考相关文献[5]进行简化，仅考虑人体模型的身躯和头部。实际情形下教室开窗一侧的外墙由砖墙和玻璃外墙组成，而开门一侧的内墙上方位置设有常年关闭的廊窗，本文暂时不考虑廊窗和外墙上悬窗的开启。模型及相关尺寸数据如图1 和表1 所示。

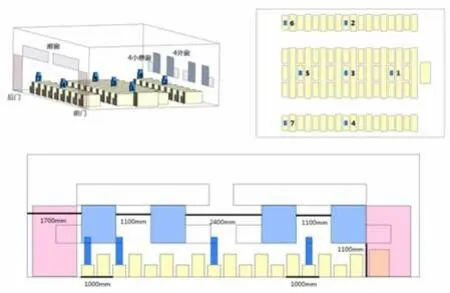
图1 教室模型示意图

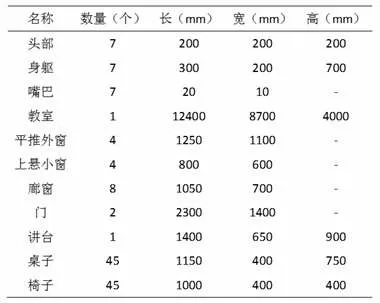
表1 人体及教室内相关布置物个数与尺寸

1.2 数学模型的选择

模拟飞沫液滴扩散的CFD 方法有欧拉-欧拉法和欧拉-拉格朗日法两种，前者将飞沫颗粒相看为连续介质，可以预测飞沫颗粒浓度分布，而后者将飞沫颗粒相看作离散相，可以对每一个粒子的运动轨迹进行跟踪[6]。何其斌等人[7]指出由于欧拉法忽略了室内颗粒物的颗粒特性，故只适用于模拟微小的能够较好跟随气流流动的中性浮力颗粒物，而拉格朗日法则主要用于预测粒子的运动轨迹和瞬态运动。本文主要研究的时咳嗽飞沫液滴的瞬态扩散过程，因此选用欧拉-拉格朗日法对咳嗽飞沫颗粒进行轨迹跟踪研究。对于室内连续场，综合计算速度和流场模拟精度要求，选择计算速度适中且能很好地预测自然通风空间流场的基于RANS 方程的标准k-ε 模型进行模拟[8]。

2 边界条件设置

本文研究的是夏季呼吸道传染病疫情爆发期间教室前后门、4 扇平推外窗完全开启时，自习状态下的咳嗽飞沫液滴的瞬态扩散。设定自习状态下教室内人数为七人，位置编号从1 到7，具体的人员分布如图1所示。七人中仅有一人为潜在患者（潜在患者标红），忽略其他人员咳嗽或呼吸时的液滴扩散影响，在设定的不同进风风速下分别对潜在患者处于位置1、位置3时的咳嗽液滴扩散进行分析。正常呼吸过程中产生的颗粒物液滴较少对室内影响较小，而咳嗽会产生更多的微粒或液滴，这些微粒或液滴会传播很远的距离[9]，所以本文忽略潜在患者正常呼吸时产生的飞沫液滴扩散。

2.1 连续场边界条件设置

自然通风空气流动的动力为室内外压力差（热压、风压或二者都有），空气流动物理过程的复杂性以及室外环境的多变性导致通风率难以预测，因此，控制自然通风以获得所需的室内环境条件具有挑战性，并且自然通风无法控制通过门窗口的气流方向，室内自然通风流场的模拟难度较大[10-11]。而有关自然通风的模拟方法主要有两种，一种是建立建筑的实际模型，根据当地的气象资料直接给定通风口的风度大小和温度。另一种是在建筑周围加一个外场，扩大计算模型，在外场的入口给定当地气象条件下对应的速度大小和温度[12]。如果对进口风速、风向、温度进行实时模拟，不仅计算成本巨大而且也很难实现，因此本文采用第一种自然通风模拟方法对进风边界条件进行简化。根据当地气象条件假设入口进风平均速度（方向垂直于进风口），并假定进风参数在模拟过程中不发生变化，即在特定的通风模式下进行稳态模拟。

具体数值设置参照《民用建筑供暖通风与空气调节设计规范》[13]选取，上海地区夏季室外平均风速为3.1 m/s，本文分别选取1 m/s，2 m/s 的进风风速进行研究，进风温度和相对湿度选用夏季通风室外计算温湿度，数值分别为31.2 和69%。进风口选用速度进口（velocity-inlet），水蒸气质量分数计算约为0.0194，出风口（门）采用出流边界条件（outflow），认为出口流动达到完全发展状态。教室墙壁、天花板、地面、桌椅表面设置为绝热壁面边界条件，仅考虑人员显热忽略潜热和辐射，人员皮肤发热率取40 W/m2[14]。

2.2 离散相边界条件设置

关于咳嗽过程的飞沫液滴，已有大量文献使用不同的方法进行了研究，加之人员个体存在差异使得研究结果略有不同。孙炜等人[15]发现初始直径大于150的飞沫液滴释放之后很快会沉降到了地板上，Chao 等人[16]通过粒子图像测速技术（PIV）发现健康志愿者咳嗽时平均呼气流速为11.7 m/s，而Zhu 等人[1]所测量的咳嗽平均气流数据为11.2 m/s。实际咳嗽过程中的呼气速度是变化的，本文对人体以咳嗽方式产生飞沫的过程进行简化——飞沫仅从嘴巴以水平方向咳出，飞沫速度与咳嗽呼气速度相同，取平均流速11.7 m/s，一次咳嗽持续时间设定为0.5 s[17]，潜在患者进行间隔时间为0.5 s 的两次咳嗽，咳嗽喷出的气流相对湿度设定为100%，气流与飞沫颗粒温度均取体温309 K，呼出气流中的水蒸气质量分数计算约为0.0372。

本文选取粒径范围为2～150 μm 的飞沫液滴为研究对象，此范围的飞沫液滴短时间内不会迅速沉降到地面上[15]，一旦携带有病原体微生物则潜在危害极大。数值模拟时将飞沫液滴的物性简化为水，密度稍微夸大设定为1003 kg/m3，蒸发温度设定为273 K，蒸发后的液滴核粒径设为初始液滴粒径的32%[18]，通过计算得出蒸发性组分（水）的质量分数约为96.6%。结合Chao 等人[16]总结的咳嗽产生的不同粒径范围的液滴数量，依据密度估算出各个液滴组的质量，再根据飞沫液滴对应的质量百分数采用python 软件对在2～150 μm 范围内非均匀分布的飞沫液滴进行Rosin-Rammler 粒径分布拟合，质量分数表和拟合图像见表2 和图2。

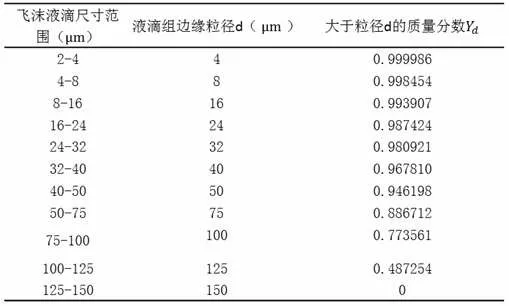
表2 一次咳嗽飞沫液滴质量分数表

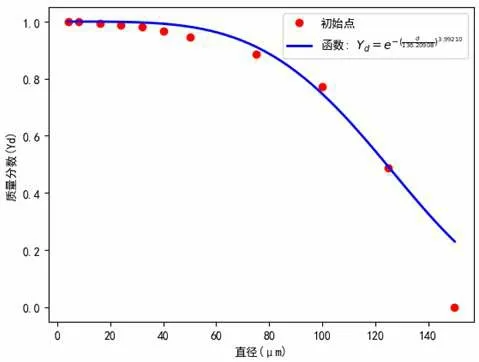
图2 咳嗽飞沫液滴粒径分布拟合

此外，设定飞沫颗粒在门窗开口，嘴巴开口处的离散相边界条件为“escape”；在室内人体表面、桌椅表面、地板的离散相边界条件为“trap”，即沉降到接触表面；而各个壁面则设为弹性壁面条件“reflect”，即颗粒到达壁面会反弹回室内空间，考虑到颗粒在壁面切向和法向上的动量损失，恢复系数均减小为0.5。

3 结果与分析

本文模拟了自然通风教室内两种进风风速下，潜在呼吸道疾病患者分别在位置1，位置3 进行连续两次咳嗽后释放的特定粒径范围飞沫液滴的分布扩散情况。由于计算机性能和内存有限，从第一次咳嗽起共模拟了100s 的咳嗽液滴扩散情形。数值模拟首先利用SIMPLEC 算法求解稳态的自然通风室内连续相流场，之后流场中加入飞沫液滴离散相并采用PISO 算法进行非稳态的两相相间耦合计算[19]，直至收敛。不同进风风速下的两种情形下的咳嗽飞沫液滴分布图如图3 所示。

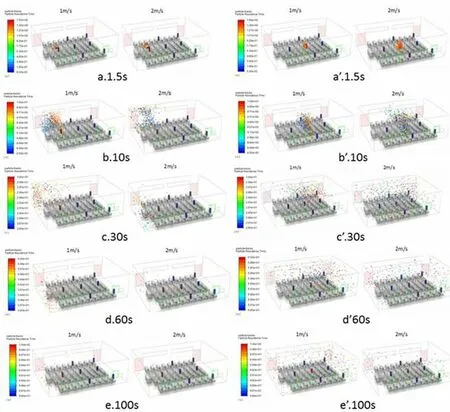
图3 潜在患者位于1、3 位置时不同进风风速下的飞沫液滴分布图

根据飞沫液滴分布图可以看出，在位置1、3 处咳嗽释放的飞沫液滴伴随着进风风速的增大，空间残留的飞沫液滴数量明显减少，位置1 右前方为飞沫液滴的主要影响区域，而在位置3 释放的飞沫液滴，由于中间两扇外窗的间距较大，位置3 没有直接位于气流流动路径上，位置3 附近存在气流回流，飞沫液滴向位置3 左右两侧空间扩散，液滴弥漫于整个教室空间，风速一定程度上加快了飞沫向左右侧的扩散。

当人员咳嗽位置确定后，进风风速是唯一变量，而进风风速对教室空间残存液滴数量的影响，可以用特定时刻的室内空间液滴包（parcels）个数与第二次咳嗽结束后的室内空间液滴包个数的比值的变化来表征，详见图4。每个液滴包可以包含多个但不限于整数个飞沫液滴颗粒。从图4 可以看出，进风风速增大可以加速1、3 位置处释放飞沫液滴的空间数量减少速度，通过对飞沫液滴的沉降，捕获，逃逸作用的促进来实现这一过程。与1 位置咳嗽情形不同，3 位置处释放的飞沫液滴在100 s 后的残存数量随着风速增大明显减少。由于教室空间较大，为了进一步了解咳出飞沫液滴的扩散情况，对潜在患者位于1、3 位置时不同进风风速下的坐姿呼吸平面高度（y=1.2 m）上的飞沫液滴浓度云图进行分析，液滴浓度云图如图5 所示。本文对浓度云图中的最大液滴浓度进行了缩放（由实际值调整缩小为1.00e-10kg/m3），以便于更好的显现出飞沫影响范围随时间和进口风速的变化情况。

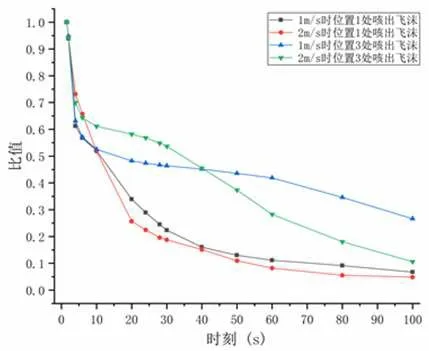
图4 不同进风风速下的教室空间飞沫液滴数量变化情况

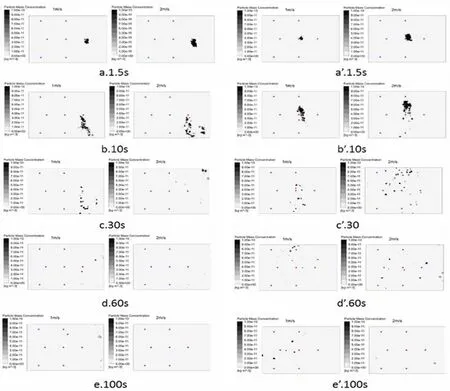
图5 潜在患者位于1、3 位置时不同进风风速下坐姿呼吸高度平面上的飞沫浓度云图

从飞沫液滴浓度云图可以看出，当进风风速为1 m/s 时，1 位置处释放的飞沫在呼吸平面上的浓度影响大约60 s 后很轻微，而增大风速为2 m/s 后该时间约提前到了30 s，飞沫影响区域局限于位置1 右前方。对于3 位置咳嗽情形，飞沫液滴的影响范围更大，影响时间更长，并且飞沫对于3 位置左侧附近空间呼吸高度平面区域的影响明显强于右侧，增大进风风速同样会加快飞沫液滴浓度向3 位置左侧的扩散。对于咳嗽位置周围飞沫液滴的具体变化情况，本文在潜在患者左右方坐姿呼吸平面高度上各截取一个1200 mm×800 mm 长方形平面，分析截取平面上飞沫液滴平均浓度随时间和进风风速的变化情况。位置3 释放的飞沫液滴向该位置左右两侧扩散，并有可能对位置2，位置4 上的人员产生影响，在位置2，位置4 前方坐姿呼吸平面高度截取相同的长方形平面，依据是否出现平均浓度非零情形来评估飞沫影响。坐姿呼吸高度小截面上的飞沫液滴平均浓度变化折线图及相关散点图如图6 所示。

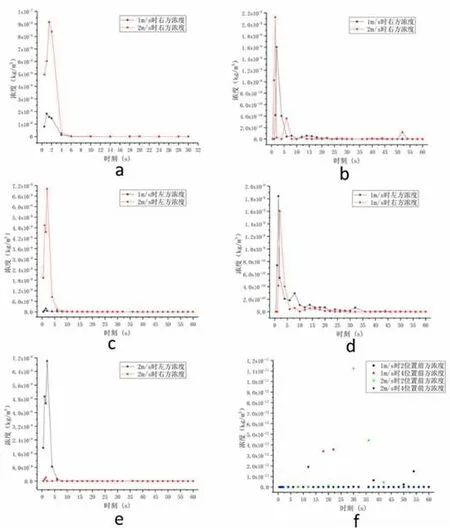
图6 坐姿呼吸高度(y=1.2 m)小截面上的飞沫液滴平均浓度变化情况

折线图a 为潜在患者在位置1 咳嗽时两种进风风速下的右方呼吸高度小平面上的平均液滴浓度随模拟时间的变化情况。折线图b，c 分别为潜在患者在位置3 咳嗽时两种进风风速下的位置3 右方和左方呼吸高度小平面上的平均液滴浓度的变化情况，折线图d，e 分别为1 m/s 和2 m/s 进风风速下的位置3 左方和右方呼吸高度小平面平均飞沫液滴浓度的变化情况。散点图f 为潜在患者在3 位置咳嗽时100 s 模拟时间内飞沫液滴对位置2，位置4 上同室人员影响情况分析。

依据图像可以看出各个呼吸高度小平面上的平均飞沫液滴浓度在1.5 s 左右到达峰值，并且峰值浓度随进风风速增大而增大。对于在位置1 咳嗽的情形，2 m/s 进风风速下的平均液滴浓度变化较为剧烈，大约在4 s 时两种风速下位置1 右方的平均液滴浓度开始平齐。对于在位置3 咳嗽的情形，当进风风速由1 m/s增大至2 m/s 后，初始时刻位置3 右侧平均液滴浓度值总体上稍有增加，而位置3 左侧平均液滴浓度则在8s 之前有大幅度提升。此外，1 m/s 进风风速下，初始时刻位置3 左右两侧平均飞沫液滴浓度差值较小，大约5s 以后左侧液滴平均浓度开始一直高于右侧，直至两方浓度平齐趋向于0。2 m/s 进风风速时，初始时刻位置3 左右侧平均飞沫液滴浓度差较大，左侧浓度一直高于右侧，大约8s 以后两侧液滴浓度开始平齐并趋向于0。位置2 和位置4 分别位于距位置3 较远的左右两侧，根据散点图f 可知：位置3 释放的飞沫液滴会对位于位置2 和位置4 的同室人员产生影响，尽管影响可能很轻微。并且相较于位置2，飞沫液滴会很快扩散至位置4 呼吸高度平面，但随着进风风速的增加，大风速下的位置2 前方的最大平均液滴浓度要高于位置4 前方的最大平均浓度，飞沫对位置2 的影响要强于位置4。

4 结论

本文在模拟过程中对进风状况，教室热边界条件，人员的呼吸状态，飞沫液滴的物性参数均进行了一定简化。得出的主要结论如下：

1）进风风速增大可以加快1、3 位置处释放的飞沫液滴数量的减少。但相比3 位置处释放的飞沫液滴，模拟时间内增大进风风速对1 位置处释放的飞沫液滴的最终残存数量影响不大。

2）对于位置1 情形，大风速时位置1 右方呼吸高度小平面上的平均液滴浓度在4 s 之前始终比小风速下的高。对于位置3 情形，随着进风风速增加飞沫液滴向左侧的扩散效应加剧，左侧平均液滴浓度在8 s之前均有大幅度提升，且同一进风风速下位置3 的左侧平均浓度在初始时刻一直高于右侧，大进风风速时左右两侧的平均飞沫液滴浓度差较大。

3）位置1 释放的飞沫液滴仅对该位置右前方区域产生影响，而位置3 释放的飞沫液滴影响范围较广，会对位于位置2 和位置4 的同室人员产生影响。进风风速的增加会加快位置3 释放的飞沫液滴向位置2，位置4 呼吸平面的扩散，飞沫向位置4 呼吸平面的扩散速度相对要快些，但大进风风速下位置2 前方飞沫液滴最大平均浓度要高于位置4 前方的最大平均浓度，飞沫在大风速下对位置2 的影响较强。