不同形状系数超瘦高中庭烟气自然蔓延研究

陶红菲 张无敌

新疆工程学院安全科学与工程学院

0 引言

中庭一般由建筑底部到顶部贯穿联通多个楼层，是建筑物的其他组成部分所围绕而形成的巨大空间[1]。北京、上海等一线城市中，因土地资源紧张，所建中庭高度节节攀升，一种形状系数ζ＜0.1，且高度匀＞50 m 的新型超瘦高中庭应运而生。

发生火灾时，超瘦高中庭因烟囱效应更加显著，烟气的蔓延过程与普通中庭存在差异，破坏性更强。但我国现有相关建筑防火规范中并未对此类特殊建筑做出针对性规定，而是沿用普通中庭的设计规范。

1 火灾模拟参数设置

对于建筑火灾而言，全尺寸实体实验需要投入大量人力、财力，且难以对同一工况进行重复实验以验证数据的准确性。计算机模拟为此类问题提供了解决方法，以其投入资金少、用时短、可多次改变参数设置重复实验工况等优点，越来越受到研究学者的青睐。本文采用FDS 软件仿真模拟与理论数值计算两种方法，进行探讨对比研究。

中庭面积在100～1000 m2的大约占有统计总数的70%，本文设置底面积20 m×20 m 为不变量，单层层高5 m。中庭形状系数为ζ。

式中：A 为中庭底面积，m2；匀为中庭总高度，m。

统计数据表明，中庭的形状系数最小值可以达到0.008[2]，例如上海交银金融大厦、北京保利国际广场T1 等建筑，本文中研究超瘦高中庭不同形状系数及对应总高度如表1 所示。

表1 不同形状系数超瘦高中庭

根据上海市工程建设规范《民用建筑防排烟技术规程》（DGJ08-88-2000），考虑最不利因素，取无喷淋中庭火灾场景（密闭空间），为简化模型，将火源设置为快速t2火，功率4 MW，火灾增长系数为0.04689。火源面积8 m2，尺寸为4 m×2 m，位于中庭的正中央，单位面积火源功率500 kW/m2（火焰临界温度1427 ℃）。

环境温度20 ℃，中庭内纵向温度梯度0.2 ℃/m。

火源正上方每升高5 m 分别设置感烟探测器、烟羽流纵向速度探测器；中庭内壁边缘竖直方向每升高5 m，分别设置感烟探测器、测量烟气层高度的层区探测设备Layer Zoning Device。

为兼顾运行时长与计算结果精确性，本文采取混合型网格，如图1 所示。火源部分及其以上空间的网格尺寸为0.25 m×0.25 m×0.25 m，其他区域网格尺寸为0.5 m×0.5 m×0.5 m。默认大涡模拟VLES（Very Large-Eddy）类型，模拟时长根据Case 不同条件，酌情控制于300～900 s 之间。

图1 中庭网格划分俯视图

2 数据分析

2.1 烟气层高度

国际常用计算烟气层高度的半经验公式[3]，不考虑排烟与补风等外界因素影响，如表2 所示。

表2 烟气层高度预测公式模型

根据FDS 中Layer Zoning Device 的设置，可直接得到数据模拟中烟气层高度随时间变化的规律。因篇幅有限，选Case4 为图示，如图2。

图2 Layer Zoning Device 测量烟气层高度

对比数据模拟与半经验公式计算结果，以Case4为例。如表3 及图3 所示：

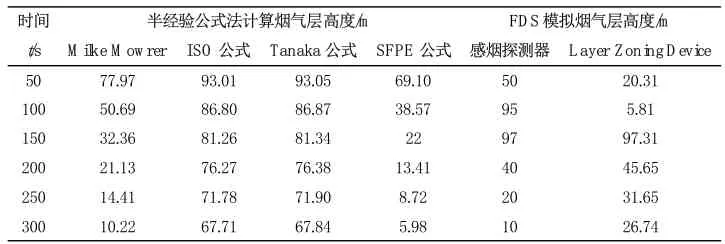
表3 Case4 烟气层高度数据模拟与半经验公式计算结果对比

图3 Case4 烟气层高度数据模拟与半经验公式计算结果对比

由表3 和图3 可知，半经验公式计算烟气层高度结果与数值模拟感烟探测器监测结果出入较大。ISO公式与Tanaka 公式不适用于超瘦高中庭烟气层高度的预测计算。Milker Mowrer 公式和SFPE 公式[4]，在烟气触顶并向下填充至250 s 后，二者计算结果和感烟探测器监测结果较为接近。

层区探测设备Layer Zoning Device 的原理是根据温度来区分热烟层与冷空气层，本文设置了温度梯度随高度变化，在火灾初期会对层高判定产生干扰，导致其所测结果与感烟探测器所测烟气层高度存在较大偏差。

2.2 烟气触顶分析

根据FDS 模拟结果，得到不同Case 中的烟气触顶时间，如表4 与图4 所示：

表4 烟气触顶时间

图4 烟气层触顶时间与中庭形状系数关系图

随着中庭形状系数ζ 的减小，虽然烟囱效应越来越明显，但是烟气的触顶时间依旧呈现增加趋势，且当形状系数小于0.02 时，烟气触顶时间急剧上升。

根据Origin 软件对离散点进行数据拟合，可得到图4 所示拟合曲线1，拟合精度达到0.97，以本文初始条件设置，所得公式如下：

式中：T0=55.85；A=196.05；B=0.0125；C=0.023。

由式（2）可知，当中庭横截面积A 与温度梯度（dTa/dZ）保持不变时，烟气触顶时间t 与中庭形状系数ζ，是以自然常数e 为底数的递减指数函数。初始条件改变，所得公式参数会有变化。

2.3 烟气触壁分析

超瘦高中庭烟气填充方式为蔓延式填充，烟气触壁过程，本文以经验公式法与数值模拟法对照分析。

常用计算烟气触壁高度的经验预测公式[5]，如表5所示：

表5 烟气触壁高度预测公式模型

用FDS 的Smoke View 窗口可以直接观测到数据模拟的烟气触壁高度，但由于人眼存在误差，本文以中庭内壁所设感烟探测器收集数据为准。Smoke View 窗口观测以Case4 为例，如图5 所示。

图5 Case4 SmokeView 烟羽流触壁观察图

对比数据模拟与理论公式计算结果，因9 个Case的底面积都相同，理论公式计算触壁高度结果相同。如表6 所示：

表6 烟羽流触壁/触顶论公式计算与数据模拟结果对比

由计算结果可知，Morton 公式计算结果与FDS 模拟数据对比明显偏大，不适用于超瘦高中庭中烟气触壁高度的计算。

NFPA92 公式与贾鹏飞修正公式计算结果接近，经验公式计算法与数值模拟的Case1、Case6、Case7、Case8、Case9 的模拟结果略有差距。其余4 个Case 的模拟结果与经验公式相比差距不大，可认为二者结果符合较好。

根据模拟结果，舍去误差较大的数值点，做出烟气分层高度ZC/总高匀随形状系数ζ 变化的图像，如图6所示：

图6 烟气层触壁高度/中庭总高度与形状系数ζ 关系图

由图6 可知，中庭形状系数越小，虽然烟囱效应更加明显，但烟气分层高度占总高的占比也越小。根据Origin 软件拟合曲线，发现二者为二次函数相关，拟合精度达到0.977，以本文初始条件设置，所得公式如下：

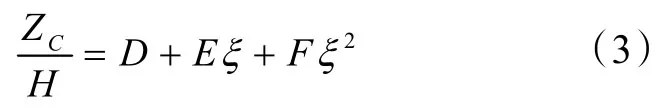
式中：D=0.086；E=5.76；F=33.29。

烟气触壁时间与中庭形状系数的关系具体如图7所示：

图7 烟气触壁时间/中庭总高度与形状系数关系图

由图7 可知，中庭形状系数越小，烟气触壁时间与中庭总高度的比值也越小。根据Origin 软件拟合曲线，发现二者为二次函数相关，拟合精度达到0.968，以本文初始条件设置，所得公式如下：

式中：G=0.17；M=16.32；I=-85.77。

3 结语

本文利用经验计算法、数值模拟即曲线拟合三种方式，对超瘦高中庭密闭空间烟气自然蔓延过程进行了探讨研究，得出以下结论：

1）ISO 公式与Tanaka 公式不适用于超瘦高中庭烟气层高度的预测计算。Milker Mowrer 公式和SFPE公式，在火灾后期烟气向下填充较低的位置时适用性较好。层区探测设备在火灾初期所测层高偏差较大。

2）随着中庭形状系数减小，烟气触顶时间增加，并在形状系数小于0.02 时急剧攀升。二者拟合曲线关系式为。

3）Morton 公式不适用于超瘦高中庭烟气触壁高度的预测计算。NFPA92 公式与贾鹏飞修正公式，二者和模拟结果也有所差距。

4）烟气层触壁高度与触壁时间和形状系数各自拟合曲线皆为二次函数相关，分别为和