裂隙岩体注浆扩散理论研究进展

张 勇 高岗荣 高晓耕

(1.煤炭科学研究总院,北京 100013;2.北京中煤矿山工程有限公司,北京 100013)

0 引 言

注浆技术作为一种经济实用的岩土加固与防渗堵水的有效手段,已在水利、交通、矿山、电力、建筑、市政等工程领域得到了广泛应用。我国注浆技术的研究与应用发展较晚,但注浆理论与技术在注浆机理、注浆方法工艺、注浆材料、实验技术等方面已有长足的发展[1-5]。注浆理论以浆液的流动运移规律为研究目标,建立扩散半径、注浆流量、注浆压力和注浆时间等因素的关系,用以指导注浆工程的设计与实施。当前,较常见的注浆理论分类有:多孔介质渗透注浆理论、裂隙岩体注浆理论、劈裂注浆理论、压密注浆理论和动水注浆理论。理论推导、模型试验、数值计算与现场原位试验作为注浆理论研究的重要手段,除原位试验受制于本身开展的难度与局限性,成果相对较少外,其余三种手段在国内外均有广泛的研究,取得了较多的研究成果。笔者对国内外裂隙岩体注浆理论的相关研究进行归纳分析,并就裂隙岩体注浆理论研究的现状与发展谈几点认识。

1 裂隙岩体注浆扩散规律的理论推导

理论推导作为研究浆液在裂隙岩体中扩散规律的重要手段,国内外专家学者建立有平行板裂隙单向扩散、平板裂隙间辐向扩散等理论模型,结合牛顿流体和非牛顿流体的本构方程,对不同条件下的扩散情况求出解析解。

1.1 优化裂隙模型求取浆液扩散解析解

求取裂隙中浆液扩散的解析解,采用的裂隙理论模型通常为平板模型。起初学者研究的都是无水或静水条件下,单一水平光滑裂隙中浆液的扩散规律,随着研究的不断深入,不少学者开始采用考虑粗糙度、倾斜以及包含动水影响的平板裂隙模型。

对于牛顿流体在水平光滑平板裂隙中的平面辐向扩散,刘嘉材推导出浆液扩散区内沿程压力降与扩散半径的公式;Baker对于相同扩散模型,利用图解法得到浆液注入量与注浆压力差的计算式[6]。DAI G 等[7]由平行板间宾汉姆流体单向扩散规律,推广得到宾汉姆流体在两平行圆盘间辐向扩散的解析解。黄春华[8]推导出水平光滑平面裂隙中宾汉姆流体的辐向流动运动方程。Mohamed[9]推导出水泥浆作为宾汉姆流体在水平光滑裂隙中辐向扩散的公式,引入黏度对扩散过程中能量耗散的影响,得出的扩散最大距离公式同Lombadi G 与Wittke W 提到的一致,并提出自身模型的假设局限性。

在水平粗糙充满地下水的裂隙中,Baker视浆液为牛顿流体,分别建立浆液流动区与水流动区的流动方程,求解得到浆液扩散半径与注浆时间的关系式[6]。Amadei B等[10]求解了一维平板裂隙(光滑或粗糙)中宾汉姆流体流动微分方程的稳态无量纲解,对比Louis成果,在压力梯度无量纲表达式分母中引入粗糙度,来间接考虑影响,认为,忽略粗糙度时(C=1),与Wallner由其他方法推导出的结论一致;恒定压力梯度时,流量公式经过化简,同经典立方定律一致。杨米加等[11]则是通过引入粗糙度影响的修正系数,对幂律流体和宾汉姆流体原本在光滑平行裂隙中的扩散公式进行调整,来考虑粗糙度的影响,并应用于有限元计算程序的编制。

对于等宽光滑倾斜裂隙中宾汉姆浆液流动模型,罗平平等[12]推导了浆液平均流速的计算式(参数包含:注浆压力水头、裂隙倾角、裂隙宽度、浆液黏度、浆液初始剪切强度和浆液密度),参照此式,通过控制变量,分别讨论各参数对流速的影响。

在单一水平光滑裂隙动水条件下,湛铠瑜等[13]建立了牛顿流体注浆扩散模型,分别求出浆液扩散与水流方向一致和相反时,扩散时间与扩散距离的关系式。Yang H 等[14]得出水平钻孔注浆时,幂律流体在倾斜裂隙中扩散距离与时间的关系式,推导出该式在动水影响下的形式,并与湛铠瑜等在单一裂隙动水注浆扩散模型中推得的解析解相比较。

1.2 调整浆液本构方程求取浆液扩散解析解

对于不同种类的浆液,由具体试验得出恰当的本构方程,并用于浆液在平板裂隙中扩散时解析求解。黏度作为本构方程中重要的流变参数之一,许多学者研究了在浆液扩散中时间、空间对黏度的影响。对于宾汉姆流体,屈服剪切应力作为其本构方程中的另一重要流变参数,也是学者们研究的一个方面。

由单一光滑平板裂隙化简来的一维平面通道,Hässler等[15-16]先是推导出仅有宾汉姆流体时的流动控制方程,在此基础上推导出通道内充满地下水、以及倾斜一维通道中包含几种不同宾汉姆流体时的流量方程,进而应用于平面裂隙网络的模拟计算。

阮文军[17]在试验中发现水泥基浆液的黏度与屈服剪切应力均随时间变化,但屈服剪切应力随时间变化不大,可视为无时变性,黏度随时间的变化规律满足指数函数分布。Zou L C等[18]认为水泥浆在扩散过程中,硬化所造成的黏度与屈服剪切应力随时间的变化都应考虑,均采用指数函数定义。

实测水泥水玻璃浆液,李术才等[19]视其为本构方程中黏度随时间变化满足指数函数的宾汉姆流体,计算浆液在等开度水平平板裂隙中的运动,求取在流量一定情况下注浆压力的分布式。张庆松等[20]基于相同的黏度时变性宾汉姆流体本构模型,对C-S浆液在静水条件下水平裂隙中的注浆扩散过程,推导出恒定注浆速率条件下浆液扩散区内黏度及压力时空分布方程。

2 裂隙岩体注浆模型试验

进行裂隙岩体注浆的模型试验需要选择简单、合理的裂隙模型,以便得到浆液压力、浆液流量、扩散距离与扩散形态等现场试验中难以直观、有效观测的重要物理量,进而揭示裂隙中浆液的扩散规律。通常学者选用不同材质的板材,平行放置于平台上,构成单一平板裂隙注浆模型,如图1所示。依照试验目的,在平板上安设压力、流量等相关参数的测量元件;为了满足一些特定试验要求,结合实际试验条件,一些学者对平板裂隙模型的具体型式做出相应的调整,用近似平板裂隙的模型进行了一些研究;另外,部分学者也尝试构建相对复杂的模型,进行多裂隙或裂隙网络的模型试验。

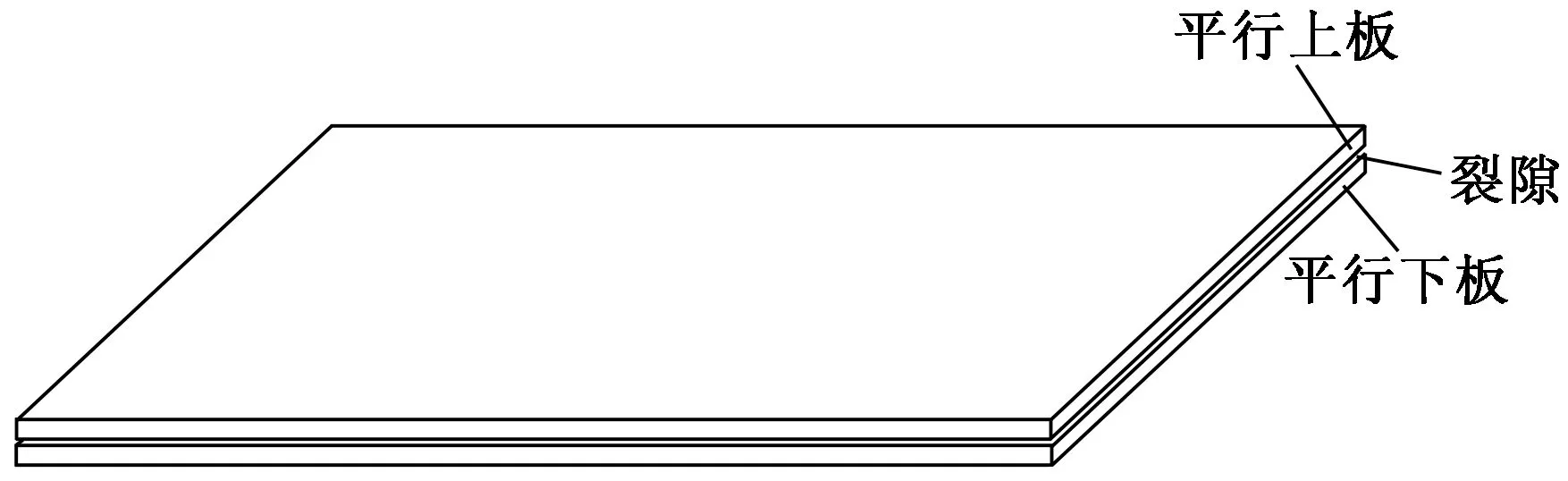
图1 单一平板裂隙注浆模型

2.1 单一平板裂隙模型试验

对于单一平板裂隙注浆模拟试验,研究的学者较多,发展也较为完善,由最初单纯研究浆液在裂隙模型中的扩散,逐渐发展到考虑实际注浆过程中裂隙的地下水环境影响。地下水环境大致分为静水环境和动水环境。静水环境在模型试验中相对较好实现,且影响因素较少;动水环境中浆液在不同裂隙情况下的扩散(包括裂隙倾角、模型边界条件、裂隙形态等),很多学者都进行了研究。

Funehag J等[21]用两块矩形亚克力板,制成平板光滑裂隙注浆装置,在板面上布置注浆孔和扩散测压孔,在两侧短边施加1 MPa以下的静水压力,用水泥基浆液进行试验。通过采集的流变参数(黏度和屈服应力)数据,对扩散影响解析解进行了验证。

张霄等[22]开发了裂隙动水注浆模型试验台,对在裂隙动水条件下的水泥浆液、抗分散浆液和化学浆液的扩散机制与封堵机理进行了研究,总结出浆液压力扩散与运移规律,为工程实际应用提供了参考。

湛铠瑜等[23]设计了动水条件下单裂隙注浆模拟试验系统,用两块有机玻璃板模拟裂隙。裂隙中除施加动水条件外,还可利用胶粘砂提供粗糙裂隙环境,可以完成扩散状态、出水采集与压力变化的监测。为了模拟裂隙粗糙度,Yang P等[24]参照Barton模型设计了木制模具,浇筑水泥浆,得到一侧裂隙起伏、满足Barton模型的透明平板裂隙动水注浆模型。

2.2 近似单一平板裂隙模型试验

除形式同图1中裂隙模型相类似的平板模型外,为更好地验证解析解、营造高水压注浆环境以及观察浆液渗滤效应,不同学者对模型具体形式做出调整,以便达到试验目的。

依据质量守恒,借助平板狭缝缝宽与圆管管径之间的等效关系,Funehag J[25]用塑料管路作为扩散路径设计试验系统,通过该装置证实了硅溶胶(黏度时变牛顿流体)扩散一维平板流动解析解。

为满足高压注浆试验要求,周兴旺[26]设计圆管状高压裂隙注浆模拟试验台,采用图2所示裂隙注浆试件。裂隙总长通过试件连接调节,测压钢管模具可以安装压力测量装置,系统整体末端可连接水压控制装置,模拟地下水。在考虑静水压力条件下,周兴旺用不同水灰比浆液在不同隙宽单裂隙模型中进行了系列试验。针对深井软岩巷道低渗透性微裂隙,王凯等[27]构造试验模型,研究了超细水泥浆在微裂隙中的渗滤效应。

图2 高压裂隙注浆模型[26]

2.3 多裂隙与裂隙网络模型试验

为了直观探索浆液在多裂隙甚至裂隙网络中的扩散情况,以便于同解析计算或数值计算结果对比分析,得出较为实用可靠的规律与算法,一些学者在单一平板裂隙模型基础上,构建多裂隙(交叉、分叉裂隙)和裂隙网络(均匀、固定夹角的裂隙网络)模型。

刘滨等[28]研制了利用预切割大理石拼装的单条裂隙和图3所示裂隙网络(含分叉与交叉裂隙)模型,用于可视化岩体裂隙恒压注浆试验系统。裂隙尺寸变化可通过大理石板微调实现,裂隙上、下各设置PMMA 有机玻璃板,整体置于不锈钢支架上,并安装摄像机和压力传感器,监测试验中浆液迁移扩散与关键位置压力的动态变化。此系统可以对注浆压力、浆液性质、隙宽、裂隙倾角进行调节。

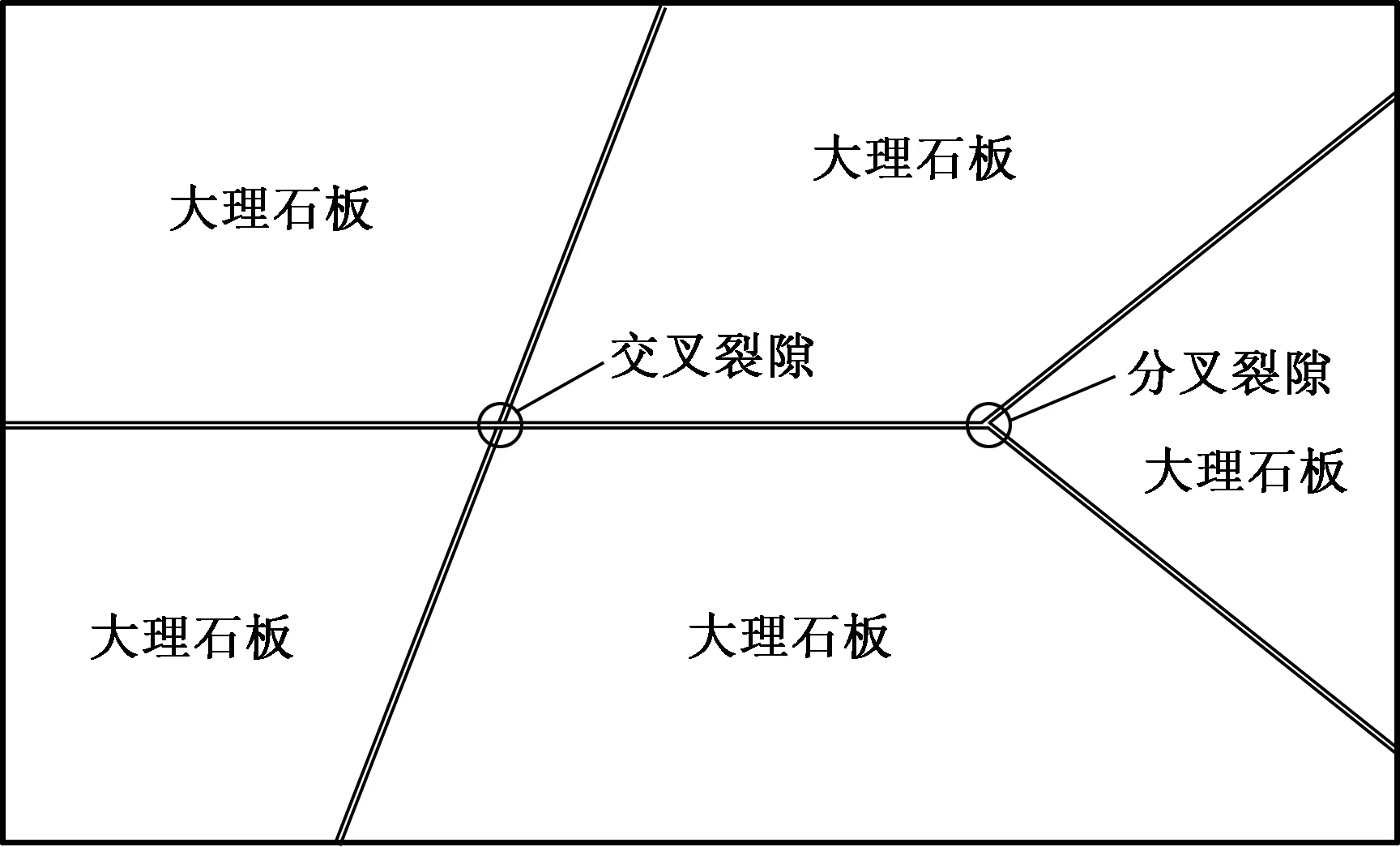
图3 多裂隙注浆模型[28]

国外也有学者利用平板间夹置方板,形成正交裂隙网络进行注浆模型试验。Hässler等[15]用两块平行叠放亚克力板,中间夹若干方板模拟岩体介质中的节理平面,用纯膨润土-水混合物代替浆液进行扩散试验,验证宾汉姆流体在含水单裂隙中扩散规律,并应用于裂隙网络的数值计算程序;Zou L C等[29]针对幂律流体在裂隙网络中的两相平流模型扩散,设计试验,采用图4所示两块平行叠放有机玻璃板,在上部板正中留孔注浆,长度方向封堵,宽度方向施加固定水头,并用玻璃板均匀地夹在其中,构成裂隙网络,利用试验数据对得到的数值解进行验证。

图4 裂隙网络模型[29]

3 裂隙岩体注浆数值计算

对国内外学者关于模拟计算的一些成果,按照学者自行编制计算程序或直接利用现有商用软件来进行分类。

3.1 使用商用软件进行数值计算

对于使用不同区域离散化方法的数值模拟软件,学者根据研究目的不同,选择不同特点的软件进行数值求解,获得所需的研究结果。

赵林[30]根据现场调查和实测数据,使用VBA 对AutoCAD 二次开发,进行岩体结构面网络模拟,生成的结构面网络,通过盒计维数法对其分形维数进行控制,随后引入UDEC,并利用UDEC可以进行固液全耦合分析的特点,考虑裂隙浆液压力与裂隙力学变形的相互影响。

方良[31]利用基于有限体积法的FLUENT 软件,对各种模型在静水条件下牛顿流体的流动进行模拟。另外采用VOF 模型对动水条件下,牛顿流体平板裂隙注浆扩散情况进行模拟分析。

COMSOL软件是以有限元为基础求解偏微分方程组,很多学者用其计算分析浆液在裂隙中的扩散。杨坪等[32]利用COMSOL 对动水环境下粗糙单裂隙中水泥浆液的扩散进行模拟,选择用四面体剖分网格,基于JRC 对裂隙粗糙度量化,用两相流模块计算扩散中浆液体积分数,用模拟结果分析扩散距离与注浆时间、注浆压力、粗糙度的关系。

3.2 自行编制算法进行数值计算

3.2.1 算法关注岩体裂隙情况

国内一些学者采用Monte-Carlo 的模拟方法,建立岩体裂隙介质的模型。郝哲等[33]得到岩体裂隙几何参数的概率分布函数和相应参数,再利用Monte-Carlo法生成服从这些分布规律的裂隙网络图形,用于注浆模拟计算程序的编制;杨米加等[11,34]利用Monte-Carlo法生成满足一定假设条件的裂隙网络,模拟包含复杂裂隙的岩体介质,再利用随机有限元计算方法,依据宾汉姆浆液在平行板光滑裂隙中的扩散规律,对浆液扩散过程中裂隙网络的单元与节点进行计算模拟;罗平平等[35]利用Monte-Carlo法,由实测裂隙几何参数建立概率模型,再用随机数产生符合模型的随机变量,用于岩体裂隙网络的生成。

为考虑裂隙粗糙度的影响,崔溦等[36]向单一光滑裂隙中黏性流体流动立方定律中引入W-M 分形函数,对立方定律进行修正,并用试验对其验证。结合岩体随机裂隙网络(DFN)模型,用修正立方定律对浆液扩散进行模拟和研究,研究三维随机裂隙网络中,粗糙度对以岩体渗透性和连通性为表征的裂隙网络特性和注浆压力的影响。

针对超细水泥浆在高压微裂隙中的渗流过程,王凯[27]对微裂隙注浆中浆液渗流与裂隙变形的耦合作用进行研究,利用MATLAB 开发步进式算法,以相同时间间隔离散浆液渗流区域,基于浆液流动与裂隙变形的控制方程建立渗流过程的理论模型,根据能量守恒和递推法对时步迭代求解,分析了裂隙开度和注浆压力对微裂隙注浆渗流的影响。

3.2.2 算法关注浆液流变参数

在裂隙岩体注浆扩散规律数值计算的研究进程中,对于浆液流变性质,起初从单纯区分浆液与裂隙中水环境,以及不同浆液间流变参数的不同,逐渐进一步考虑浆液本身流变参数在注浆过程中的变化情况,不但引入浆液流变参数随时间变化对扩散规律的影响,而且还需要考虑浆液在流动扩散过程中空间位置与时间的交互影响。

Hässler等[15-16]在研究之初,宾汉姆流体在单一通道中的扩散控制方程,在考虑地下水时对含水一维平面通道网络中浆液渗流情况,采用模拟计算方式求取数值解;另将Wallner公式推广至考虑地下水后,再推广到不同宾汉姆流体在单一倾斜通道中的流动,并将其应用于模拟程序,求解三维通道网络中交叉节点处压力变化;对于浆液在充满水的裂隙中扩散,Zou L C 等[18,29]视浆液为宾汉姆流体,水为牛顿流体,利用有限元方法求解,凭借界面压力场连续的优点,用拉格朗日方法确定浆-水界面;参考Hässler求解两相流数值方法,求取考虑浆液硬化的一些算例数值解,并进行分析,将求解两相流算法推广到幂律流体,应用于隙宽满足两点分布的裂隙网络中。

在固定注浆流量的条件下,考虑浆液黏度时空变化,对牛顿流体在粗糙的倾斜单裂隙中的辐向扩散,Mu W Q 等[37]利用MDS-SSM 算法,量化JRC值描述微元的隙宽,引入浆液扩散控制方程,计算环形微元间的压力变化,最终完成对整个扩散区域内的压力分布的估算。

对于浆液在裂隙中扩散进行的数值模拟,单纯考虑浆液流变参数随时间的变化,忽略流变参数的空间变化特性,会造成浆液在模拟注入过程中参数时变性的非正常累积。潘东东[38]提出一种注浆分序扩散固化模型与数值模拟方法(SDS方法),分序次对浆液赋予不同黏度时变函数,解决了因浆液黏度时空变化难以表征和数值实现的问题。

4 结论与展望

(1)笔者针对注浆理论研究中一个重要的分类——裂隙岩体注浆理论研究,从三个主要研究手段方面对国内外学者的研究成果进行评述。由于实际注浆条件的复杂性,依靠理论推导求取解析解或是单纯通过模型试验寻找规律,在时间、成本和精力上都不如模拟计算高效。未来相关裂隙岩体注浆理论的研究,应当用理论推导为指引,以模拟计算为主,辅以模型试验验证。

(2)未来研究需要进一步发展的方向:

在同一注浆段内,浆液在平行并存或交叉、分叉的裂隙中扩散时,对各裂隙中浆液相互间耦合规律研究;

当前研究成果较多的还是平板裂隙模型或与之相近的模型,较复杂的裂隙网络大多属于均匀分布裂隙,基于概率统计的随机裂隙网络也有一定发展,关于裂隙的描述能否更加合理,以满足生产实践的需要,有赖于相关现场裂隙岩体测量与评价手段的进一步发展,进而完善裂隙岩体注浆理论研究;

对于裂隙中地下水环境的控制,现有研究基本集中于低压或无压状态,少有在10 MPa以上的水压环境中对浆液扩散进行研究的报道,这与当下注浆技术在深部地下工程中的广泛应用是不相匹配的;

裂隙岩体注浆研究多集中于水泥基改性浆液和化学浆液,应加强对煤炭行业广泛应用的黏土水泥浆的研究;由于测量与定义方式囿于现有理论限制,缺乏更符合实际情况的浆液本构方程用于扩散理论;针对浆液流变参数在实际工程中应用时的变化规律,应当采取更加行之有效的描述或评价方式,以使理论研究更加贴近实际。