基于大数据分析的汽轮机缸效劣化研究

金宏伟，徐云柯，邵建宇，王丽娜，苑志猛

（1.浙江浙能台州第二发电有限责任公司，浙江 台州 317109；2.浙江浙能电力股份有限公司，浙江 杭州 310063；3.山东鲁软数字科技有限公司，山东 济南 250001）

0 引言

汽轮机作为发电机组将蒸汽热能转换为机械能的核心设备，其设备效率直接影响机组的能耗水平［1-3］。而随着其设备运行时间的增长，其各项性能指标必将逐步劣化。通过分析历年运行数据，掌握汽轮机缸效率的劣化趋势，对电厂的安全运行和节能降耗有着重要意义。传统方法通常需要进行大量试验获取高压缸性能数据分析劣化趋势，试验周期较长，成本代价大，且试验数据往往不能满足全工况分析要求。

20 世纪90 年代以来，通过分析大数据逐步成为工业优化领域方向重要的方案［4-5］。文献［6］使用ARMA 模型预测方法，用历史数据预测得到的预测值与实际值做对比得到劣化数值，以此方法得出的劣化数值与预测模型的精确度有较大关系，难以保证其结果准确性，文献［7］提出了利用经验模态分解方法与特征流通面积去计算劣化数值，而这种方法无法对后期微小劣化算得结果。

从电厂实际运行数据入手，采用一种完全基于历史数据的数值分析方案，通过对历史数据进行处理，以理论经验为基础设置工况判别条件，结合大数据分析手段挖掘并处理，在大量杂乱的历史数据中筛选出真实有效且符合理论依据的缸效劣化结论。

1 算法原理

1.1 最小二乘法矩阵运算

最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配，由Adrien-Marie Legendre 在19世纪提出［8］，E(w)=∑(y-wx)2，其中y表示多组样本的观测值，wx为假设拟合函数的理论值，目标函数E(w)即为损失函数。

假设函数y=anxn+a(n-1)x(n-1)+...+a0，其中y为因变量，x为自变量，目标为求系数an、a(n-1)、a0将其构建矩阵

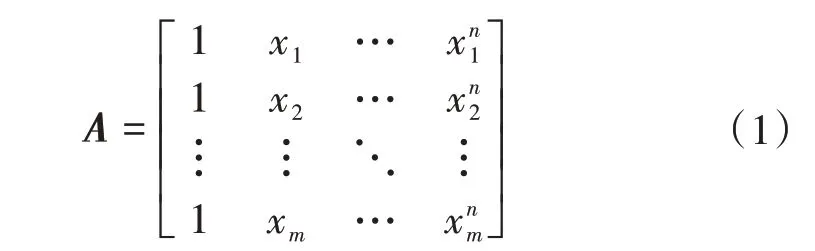
目标方程为Aw=Y，w=[a0，a1，…，an]T，Y=[y1，y2，…，ym]T，在m=n的情况下有w=A-1Y，在m≠n的情况下有ATAw=ATY，令T=ATA，则 得到（2）式：

1.2 SG滤波法

SG 滤波法（Savitzky Golay Filter）也称多项式滤波，核心思想为对窗口内数据进行加权滤波，本质上同是一种基于最小二乘原理的多项式平滑算法的信号处理方法［9-11］。相比于滑动平均法、指数滑动平均法，SG 滤波法在滤波平滑过程中能够有效地保留信号的变化信息。

设滤波窗口长度为n=2m+1，使用k阶多项式对窗口长度内数据点进行拟合，信号x(t)可以表示为时间t的函数

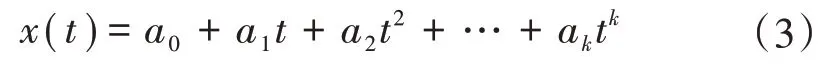
令θ=[a0，a1，…，ak]T为模型的参数向量，r(t)=[t0，t1，…，tk]T为回归变量，则得到

在已知n个这样的方程后，应用最小二乘法确定拟合参数θ的最优估计

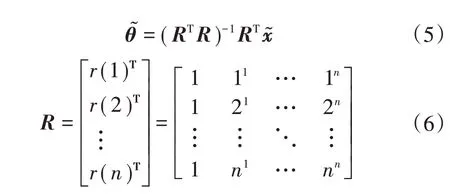
在计算出矩阵后，即可快速地将观测值转为滤波值，某时刻电厂负荷数据滤波前后效果如图1。

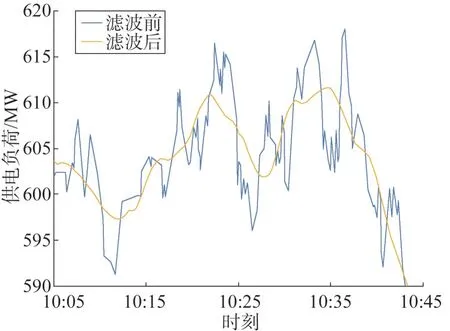
图1 SG滤波效果

1.3 MCD异常检测算法

最小协方差行列式（Minimum Covariance Determinant，MCD），是一种常用的多元位置参数和尺度参数抗差估计，而MCD 异常检测算法核心为利用均值向量与协方差阵，结合马氏距离计算思想得到更准确的离群点探测，属于一种鲁棒性很强的位置和分布估计算法［12-15］。

假设有一组数据有n个样本，每个样本包含p个元素，构成矩阵

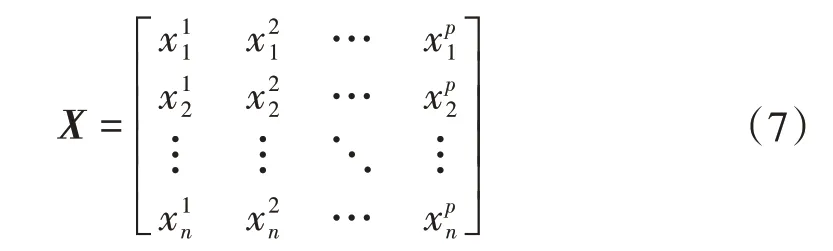
经典的容忍椭圆定义为一组数据x，马氏距离为

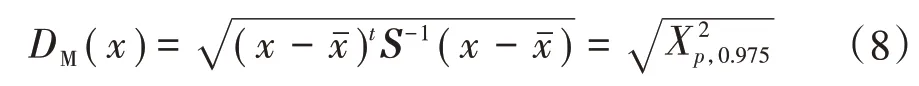
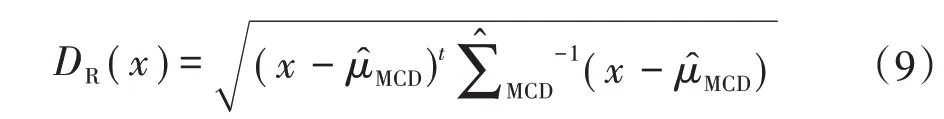
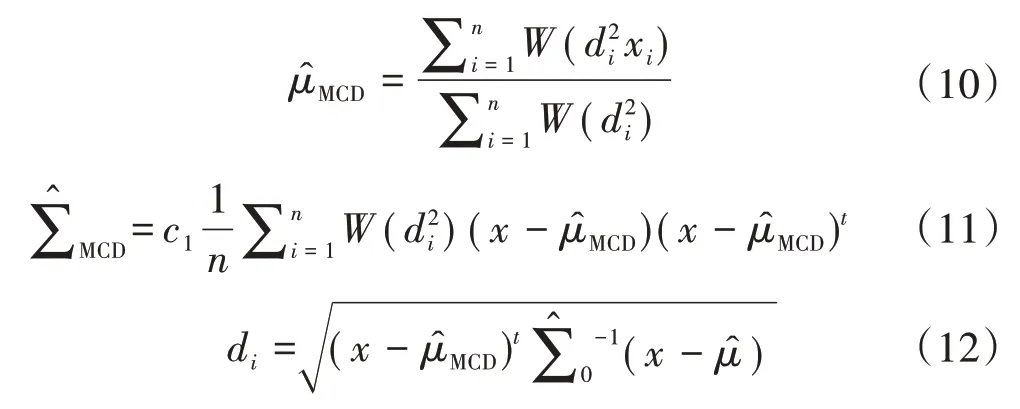
式中：W为权重函数；c1为一致性因子；为数据集的协方差矩阵；W最为快捷有效的选择为

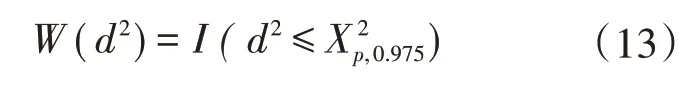
2 具体流程

流程分为10步，如图2所示，首先对历史数据进行稳态非稳态识别与筛选，找到机组运行稳定阶段的有效数据；通过等间距的划分负荷与调阀参数的距离区间，将原始数据划分成若干个区块作为工况划分；分别对每个区块进行包含异常值与小样本工况剔除的数据筛选工作；对筛选后的数据集计算高压缸效率；等间距划分，将数据集中的z轴（即高压缸效率）分为多层；对调阀与负荷两个测点扩维，通过最小二乘法拟合权重方法进行曲面拟合，并对各层缺失数据的区块进行填补；对各年各区间数据进行统计与分析历年高压缸效率值，根据历年高压缸效率值的变化情况即可得到汽轮机高压缸的具体劣化情况。具体步骤如下。

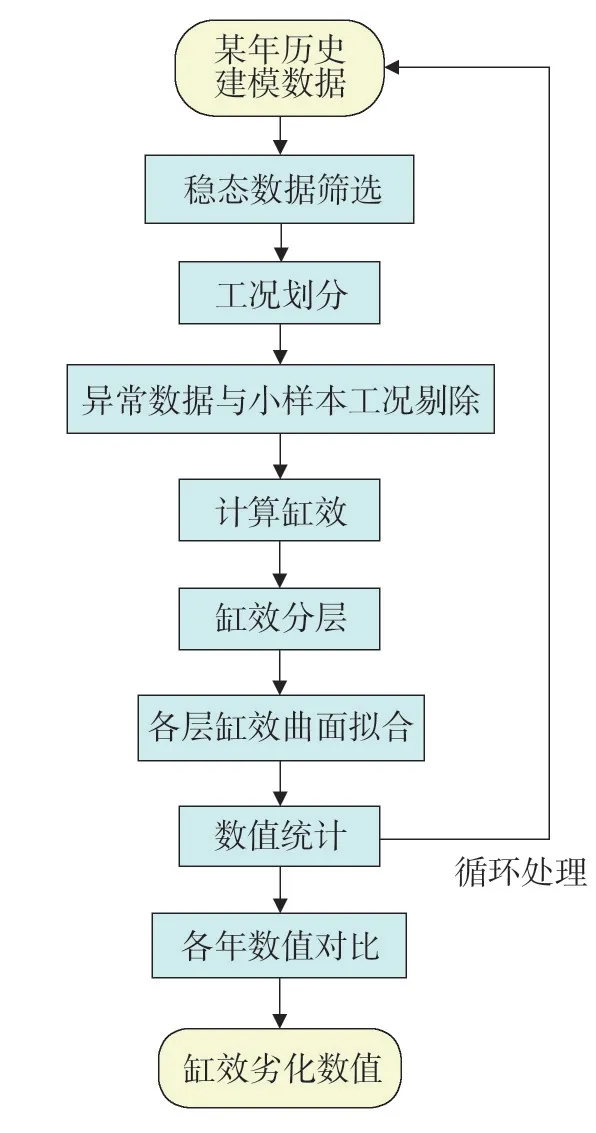
图2 高压缸劣化研究流程

1）获取某年历史数据中与高压缸效率计算相关测点。

2）通过对相关测点进行稳态识别，具体步骤包含：分别对各个参数的历史数据进行多项式滤波，得到新的数据集；对滤波前的数据指定时间窗口T1，计算其时间窗口内数据的方差，滑动时间窗口，得到方差数据集；对滤波后的数据集时间窗口T1内数据进行一阶线性拟合，滑动时间窗口得到的斜率数据集；通过设定合适的方差与斜率的阈值，在方差数据集与斜率数据集筛选同时处于方差与斜率阈值内时间段的数据，判定其时间段内的数据为稳态工况数据。

3）通过不同的负荷与调阀开度对数据进行工况划分，将稳态工况数据集分为若干个区块。

4）对样本量足够多的区块进行保留，若该工况下样本量低于N条，则舍弃该区块下全部数据。随后对不同区块下的数据使用MCD算法进行异常值剔除。

5）对步骤2）处理后得到的新数据集进行逐条计算高压缸效率，得到缸效数据集。

6）对不同的区块获取其历史最大缸效值与历史最小缸效，按照其差值将其等间距的划分为10 层。再将不同工况下相同层的数据进行合并得到同层数据集，共10个。

7）对同层数据表进行负荷、调阀与缸效之间的进行扩维后再使用最小二乘法拟合各个参数与缸效之间的权重，共得到10 个不同的非线性回归拟合模型。

8）将稳态数据中每一条数据的负荷与调阀分别带入10 个非线性回归拟合模型中得到10 个推算缸效值，并与业务计算得到的计算缸效值做差，找到其距离最近（差值绝对值最小）的推算缸效值。并将距离最近的推算缸效值所对应的模型建立层级视为该历史数据的层级。

9）对所有稳态数据都按上一步骤获取层级，统计不同层级下不同负荷调阀工况下的高压缸效率均值与样本量。

10）再代入下一年的历史数据，重复上述步骤，比较两年历史数据10 层中的均值与样本量即可得到其高压缸性能变化数据。

3 算例测试

以华南某电厂百万机组高压缸的数据对本文所提方法的有效性进行验证，使用2016 年1 月1 日00：00 至2019 年12 月31 日24：00 的数据进行逐年建模分析。

3.1 数据获取

测点共选取主蒸汽压力、大气压力、主蒸汽温度、高压缸排汽压力、高压排汽温度、机组负荷、调阀开度共计7项指标。

利用厂级信息监控系统选取2016—2019 年共计4 年的运行数据，为保证后续稳态数据筛选精度，采用5 s 一条的采样频率进行插值取数。每年样本量均为620 万条。通过前5 项指标主蒸汽压力、大气压力、主蒸汽温度、高压缸排汽压力、高压排汽温度通过业务计算得到每条数据的计算缸效值。

3.2 稳态数据筛选

对4 年数据的机组负荷与主蒸汽压力分别进行多项式滤波算法，通过选取某点前后各30 条数据进行该点数据的2阶多项式拟合计算，最终得到4年每年620 万条数据的新扩维参数机组负荷滤波值与主蒸汽压力滤波值。

由于在负荷与主蒸汽温度稳定的情况下缸效在短时间内即可以稳定，不会有很强的滞后性，故这里分别对机组负荷滤波值与主蒸汽压力滤波值通过滑动时间窗口10 min，步长为5 s 的方式逐段进行一阶线性拟合，将一阶线性拟合出的斜率作为该段滤波后数据的斜率，得到4年每年620万条数据的新扩维参数机组负荷斜率与主蒸汽压力斜率。

分别对机组负荷与主蒸汽压力进行原始参数的方差计算，选取与步骤2）滑动相同时间窗口10 min与步长5 s 的方式逐段计算方差，得到4 年每年620万条数据的新扩维参数机组负荷方差与主蒸汽压力方差。

通过设定合适的斜率与方差阈值，这里通过分别计算两个测点的斜率与方差频次分布直方图。在斜率频次分布直方图获取其拐点附近合适的数值作为斜率阈值设定值；在方差频次分布直方图获取其双峰结构中的波谷点附近合适的数值作为方差阈值设定值（前峰为稳态数据集中分布峰，后峰为非稳态数据分布峰）。2016 年斜率频次分布如图3 所示，方差频次分布如图4所示，最终斜率阈值选定0.035，方差阈值选定7.6。

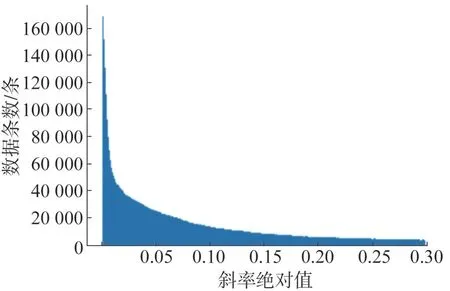
图3 斜率频次分布

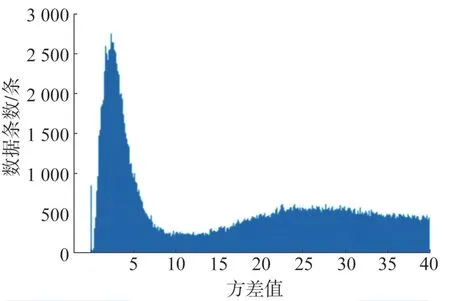
图4 方差频次分布

通过上一步中所得阈值对数据进行筛选，阈值内的作为其稳态数据段，阈值外的作为非稳态数据段。

对所得每段稳态数据各剔除首尾各6 条数据（30 s）。

最终在稳态筛选完成后，2016 年数据留存181万条，2017 年留存194 万条，2018 年留存187 万条，2019年留存202万条。

3.3 各工况下异常数据剔除

以2016 年相关数据为例，分别计算在稳态识别前调阀开度、负荷与高压缸效率的spearman 相关系数，得到负荷与高压缸效率的相关系数为0.31，调阀开度与高压缸效率的相关系数为0.76；稳态识别后负荷与高压缸效率的相关系数为0.14，调阀开度与高压缸效率的相关系数为0.93。其余3年的相关系数数值也表明其调阀开度与高压缸效率相关性较强，负荷与高压缸效率相关性较弱。

由步骤1）的结果得出结论，稳态条件下，缸效与调阀开度有绝对正相关关系，与负荷关系较弱，因此以调阀开度每1 个单位，负荷每10 个单位从业务逻辑上划分工况，将数据分割区间。

由于机组运行条件下负荷范围为400～1 050 MW，调阀开度为20%～97%，所以在将稳态数据按步骤2）条件分割区间后，共产生65×77 块数据，分别对每一块数据运用MCD 算法进行异常值剔除，以此保证异常值剔除的准确性。

在异常值数据剔除完成后2016 年数据留存174万条，2017 年留存186 万条，2018 年留存180 万条，2019 年留存196 万条。剔除异常值后数据的三维散点图如图5所示。

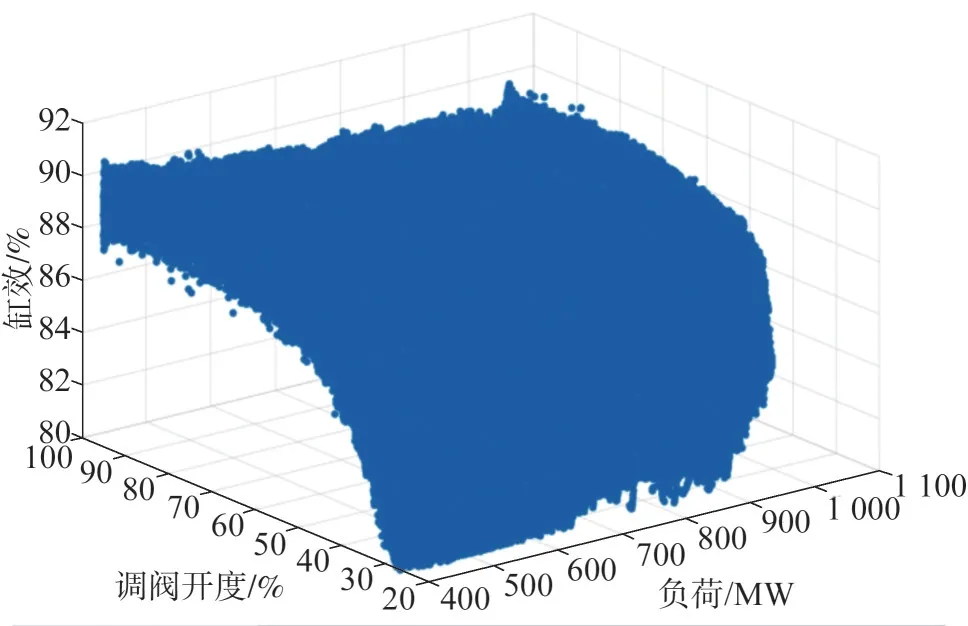
图5 剔除异常值后数据的三维散点图

3.4 数据分层

分别统计上述每一个工况下数据量，若数据条数低于500，则将该区间下的数据全部舍弃，未舍弃的数据则统计其最大值与最小值，将其按照等间距方式在最大值与最小值中划分成十层；再将该工况下的所有数据分别放入十层中，以此类推将全部工况下的数据放入十层中，以此达到模糊工况划分的目的。

3.5 缸效拟合与曲面构建

由于在机组真实运行阶段会出现某些工况的发生次数较少或完全不出现，故需要对这些未发生的工况或者发生次数较少因此在分层阶段中舍弃掉的数据进行推测补全。

同样基于前述其2016 年两个相关系数分别为0.93 与0.14 的原因，假设其调阀开度、负荷与高压缸缸效有直接关系，故可以简单地用其前两个参数推算高压缸缸效。以缸效率作为因变量Yk，调阀开度、机组负荷作为自变量，分别计为a，b进行3阶扩维，得到参数a，b，ab，a2，b2，a2b，ab2，a3，b3，加上常数项z的后的权重分别为w1，w2，w3，w4，w5，w6，w7，w8，w9，w10最终得到

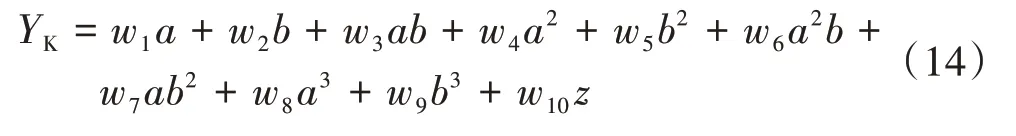
将2016 年各层现有数据作为训练数据，通过最小二乘法拟合式中各参数权重w1，w2，w3，w4，w5，w6，w7，w8，w9，w10，最终分别得到十层数据拟合出的各层公式作为各层的非线性回归拟合模型。

在填入全部数据后，得到2016 年十个非线性回归拟合模型的曲面，各层曲面图形极为相似，但其在高调阀开度上的，相同调阀开度与相同负荷对应下的缸效值会有明显差异，以其中第1 层为例曲面图形如图6所示。

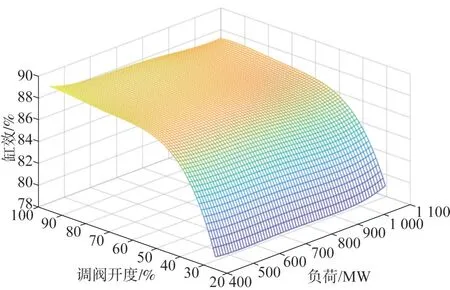
图6 2016年第一层数据回归拟合曲面图

3.6 数值统计与比较

将前述数据分层步骤前的2019 年全部数据逐条利用其机组负荷和调阀开度两个参数代入至基于2016 年数据的十个非线性模型中，得到推测出的十个推算缸效值。

将该条数据的计算缸效值与推测得到的十个推算缸效值进行差值计算，统计与其差值绝对值最小的推算缸效值隶属于基于第几层数据所建立的非线性回归预测模型。则该条数据应属于第几层。

在将剔除异常值的稳态数据全部统计完后，分别对每一层不同工况数据计算其均值，则当年处理年份的数据获取完毕。

在用同样的方法将2016—2019 共4 年的数据全部统计完毕后，通过选取其具有典型性与代表性的几种运行工况，分别得到该工况下每一年数据每一层数据的均值。

通过对4 年均值进行逐条对比即可得到其高压缸在未发生异常情况下逐年劣化情况。

展示算例中所选机组在2019 数据各层的均值如表1所示，各年各层平均缸效数值如表2所示。

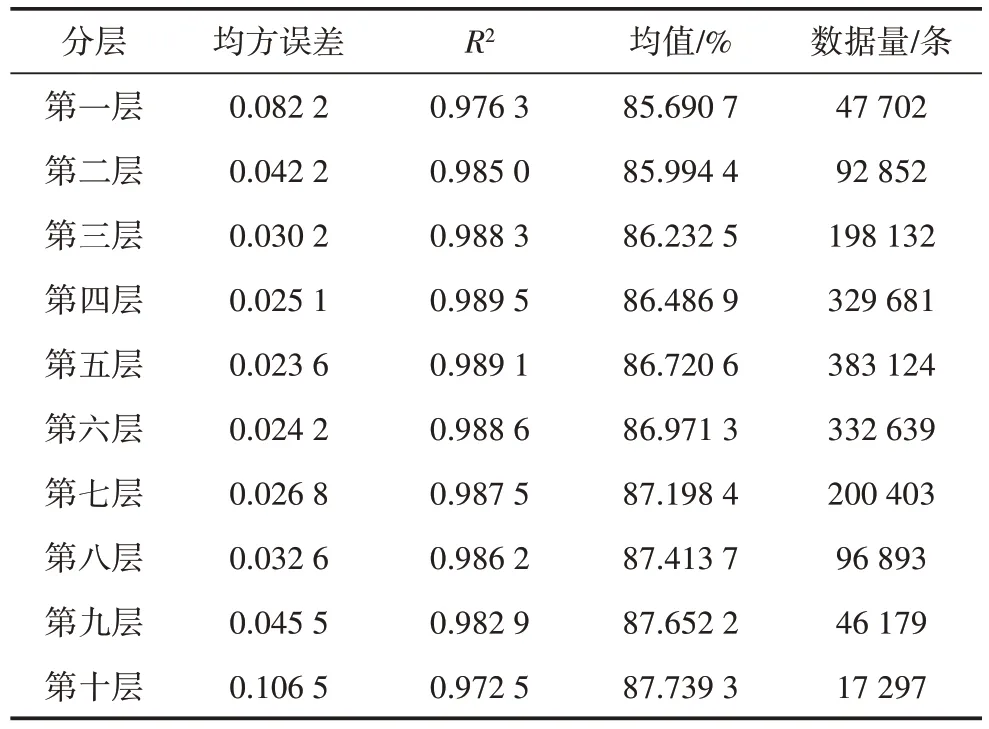
表1 2019年各层非线性拟合函数各项数值

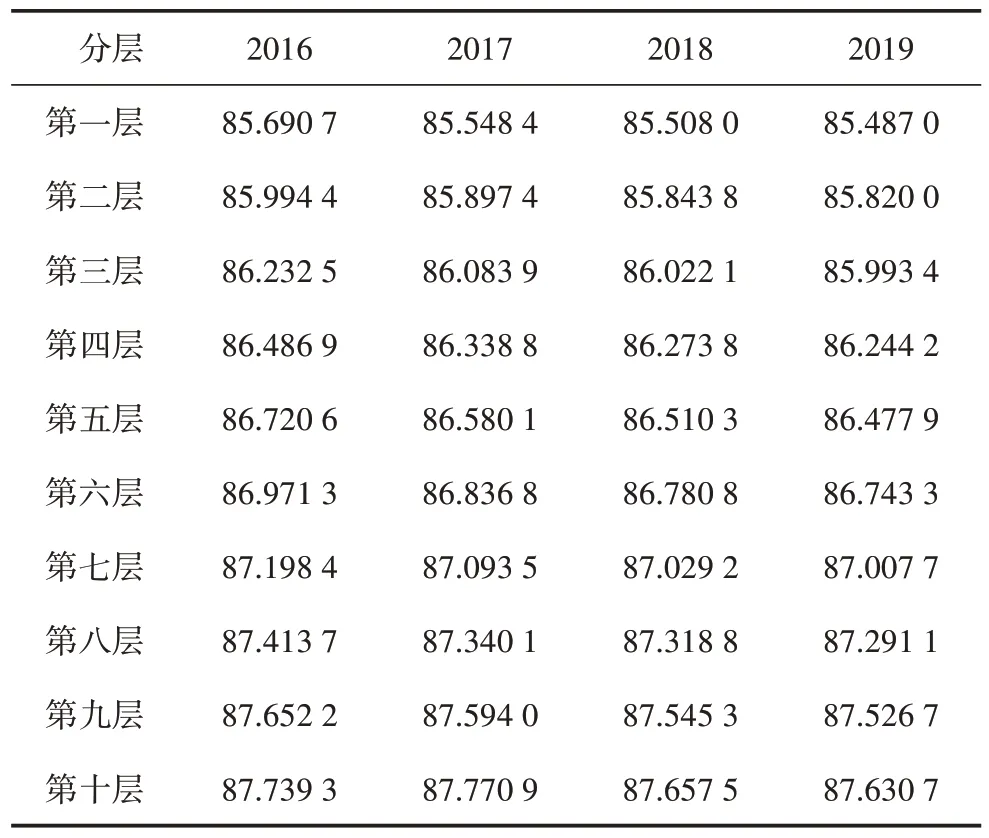
表2 2016—2019年各层拟合后缸效平均值 单位：%

4 结语

将大量历史运行数据进行处理分析，得出了高压缸性能逐年劣化趋势的具体数据。机组在2016 年至2019 年中，基本展现出以每年0.03%～0.15%的劣化趋势发展，如图7 所示，其中2016 年至2017 年平均劣化0.143%，2017 年至2018 年平均劣化0.06%，2018 年至2019 年平均劣化0.03%。利用该方法不仅能够做到较为准确地劣化数值，用于分析设备劣化情况，对机组的运行及优化同样具有着指导意义。以该方法得出的劣化趋势数据为基础，分析近期高压缸性能数据亦可进行短期设备风险预测，若设备参数偏离正常劣化区间则可判别高压缸内发生异常情况，为机组的安全评估与能效优化方面提供帮助。

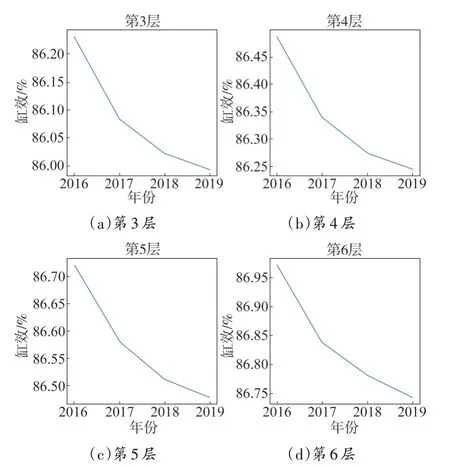
图7 2016-2019年各层缸效