变压器运行数据缺失值修复研究

秦佳峰，周 超，林 颖，白德盟，郑文杰

（国网山东省电力公司电力科学研究院，山东 济南 250003）

0 引言

随着电力系统信息化程度的提高，电网的运行和监测数据均呈指数级增长［1-3］。巨量的数据为智能调度和决策提供了信息基础，但也对数据处理手段提出了更高的要求［4-6］。变压器作为电网中的重要一环，其运行数据对后续的设备状态评估至关重要，但是由于设备故障、通信故障、操作失误等原因，实际取得的运行数据往往存在缺失的情况，从而降低后续数据挖掘算法的性能。因此，修复缺失的变压器运行数据对提升智能电网的运行效率，提高电网系统的可靠性和自愈能力至关重要。

关于电力系统缺失数据的修复，目前已有多种方法［7-9］。张晓星等［7］基于聚类的思想计算电力负荷曲线的特征函数，利用该特征函数修复缺失数据，但这种方法对数据的日曲线相似度要求很高。严英杰等［8］将输变电设备状态数据看成时间序列，用差分整合移动平均自回归模型（Autoregressive Integrated Moving Average，ARIMA）拟合并迭代检验的方法修复缺失数据，但这种方法利用的信息较少，且不适合连续缺失的情况。刘沅昆等［9］提出了一种基于Pearson 相关系数的历史数据挖掘恢复方法，但这种方法本质上是在做线性回归，很难刻画出数据的实际波动情况。

通过分析真实的变压器运行数据，希望找到一种缺失数据修复方法，不仅能利用不同日曲线之间的相似性，并且适用不同的缺失点分布情况。函数型主成分分析（Functional Principal Component Analysis，FPCA）作为一种高维特征提取方法，能够通过对同一观测对象的重复测量，在低维函数空间上表示出数据最主要的波动情况［10-11］，能够很好地拟合出数据波动的整体趋势。小波变换作为信号处理的常用方法，能够通过对函数的多尺度细分，聚焦函数的局部细节，提取出其中的有效信息［12］。

因此，结合FPCA和小波变换处理函数型数据的优势，提出了一种变压器缺失数据修复方法。该方法能够自动提取数据波动的特征，并使恢复所得的数据在局部上更符合实际情形［13］。

1 FPCA原理

1.1 根据FPCA构建模型

具体到变压器的运行数据修复，考虑其中一类运行数据，可以将第i天内变压器的该类运行数据视为一个观测对象Yi，传感器在第j个观测点对应的时间点tj测得的数值Yij为该时刻的观测值，记第i天的观测点数量为ni。由于同一个变压器在连续的几天内运行数据的波动趋势有一定的相似性，因此可以将N天的数据Yij，1 ≤i≤N，1 ≤j≤ni视为一组纵向数据进行分析。首先，利用FPCA 方法估计函数型数据的低频部分Xi(t)。根据Karhunen-Loève 表示［14］，Xi(t)可表示为

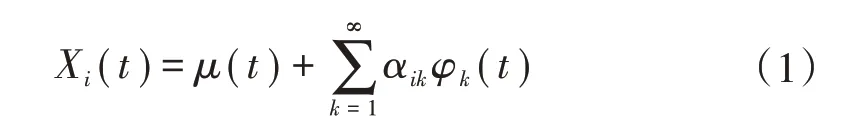
式中：μ(t)为均值函数；φk(t)为协方差曲面的特征函数，即主成分；αik为Xi(t)在主成分上的得分。

利用FPCA方法分别估计均值函数μ(t)、特征函数φk(t)、系数αik。由于通过FPCA方法估计的Xi(t)忽略了数据高频部分的信息，利用小波刻画函数数据细节的能力，通过对残差函数ξi(t)做小波变换，提取出其中高频部分的信息。因此整体模型可以改写为

关于残差函数ξi(t)的处理将在下文叙述。同时，将第i天的第j个测量时间点tj记为Tij，将观测值Yi(tj)记为Yij。

1.2 均值函数及协方差曲面估计

采用加权最小二乘的方法估计均值函数μ(t)。对某一固定的时间点t，假设β0(t)和β1(t)为两个参数，其中β0(t)为均值函数μ(t)的估计，β1(t)为线性修正函数的斜率，因此Yij-β1(t-Tij)即为t时刻Yij对应的修正值。取高斯核函数为权重值，因此，可通过求解如下极小化问题得到对均值函数μ(t)的估计为

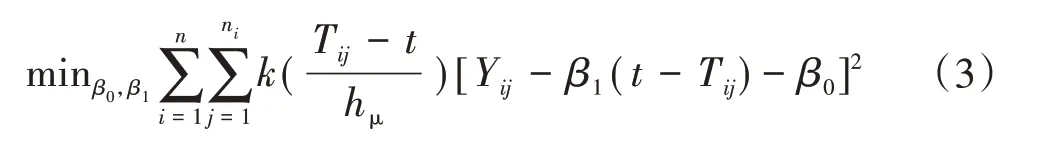
式中：β0、β1为关于时间t的参数函数；hμ是带宽，为了使算法有更强的自适应性，采用广义交叉检验的方法选择带宽；k(·)是高斯核函数，其表达式为

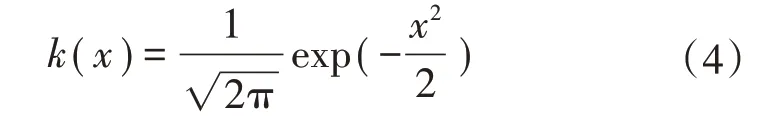
通过求解式（3）中的极小化问题，得到对均值函数μ(t)的估计为

对协方差曲面的估计同样可以采用加权最小二乘的方法。与估计均值函数μ(t)一样，对某一组固定的时间点(s，t)，β0(s，t)，β11(s，t)和β12(s，t)都是待估计的参数，其中β0(s，t)为对协方差曲面G(s，t)的估计，β11(s，t)和β12(s，t)分别为两个方向上线性修正函数的斜率。

首先估计在s≠t时的协方差曲面，可以通过求解如下极小化问题得到，即为

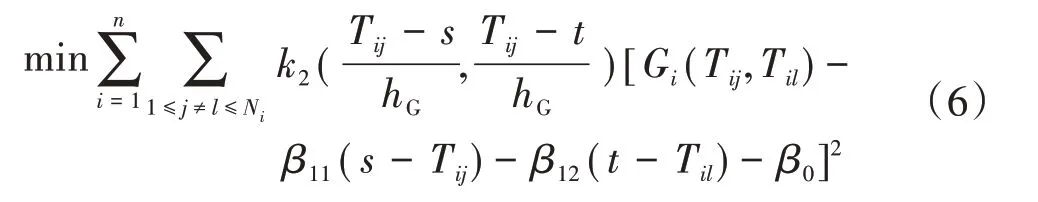
式中：hG为带宽，可通过广义交叉检验的方法选择带宽；k2(·，·)为一个二元高斯核函数。k2(·，·)和Gi(Tij，Til)的表达式分别为：

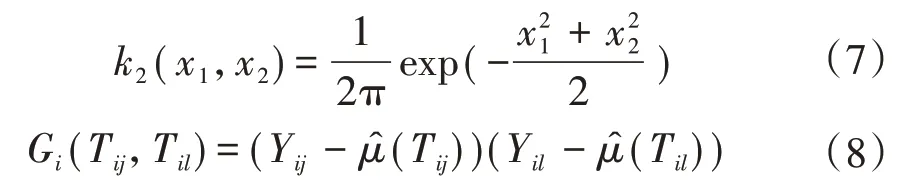
通过求解式（6）中的极小化问题，得到在s≠t时协方差曲面的估计为

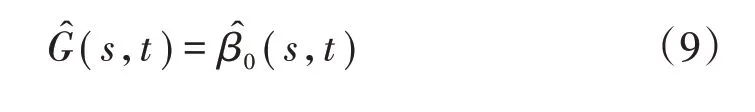
当s=t时，由于协方差曲面在垂直对角线方向上的形状更接近于二次曲线［15］，在垂直对角线方向上用二次函数修正，而在对角线方向上仍采用线性函数修正，将坐标轴顺时针旋转45°，即为

结合式（9）和式（11），可得对协方差曲面的估计(s，t)。

1.3 主成分的选取及主成分得分的估计

主成分是协方差曲面的特征函数，因此可以通过求解式（13）的积分方程得到对特征函数的估计。

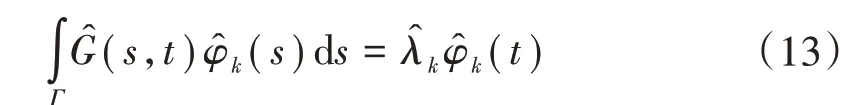
具体的，通过将协方差曲面离散化，得到K组特征值和特征函数1 ≤k≤K，需要选取其中最重要的k个主成分。为此，定义方差解释比（Fraction of Variance Explained，FVE）为

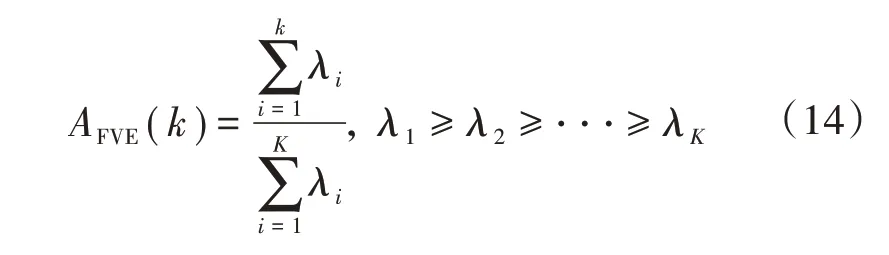
给定一个阈值θ，选择前k个最大的特征值和对应的特征函数，使得AFVE(k)≥θ，完成对主成分的选取。

最后用条件期望来估计主成分得分αik，记

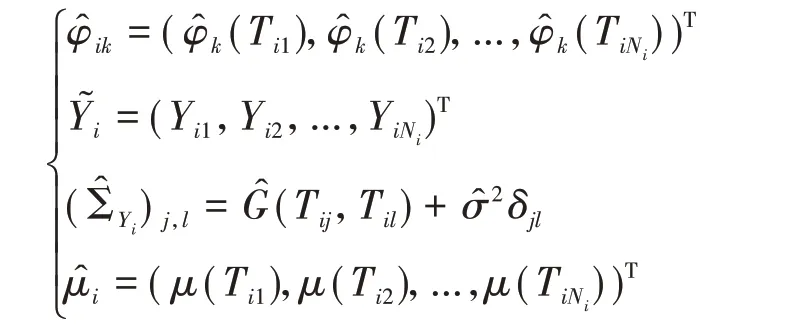
其中δjl在j=l时为1，j≠l时为0，Γ为t的定义域为

该函数能够较好地近似函数型数据的整体波动趋势，但是在局部细节方面存在过于平滑的现象，因此需要分析真实值与估计函数做差得到的残差函数ξi(t)，通过用小波变换提取其中的高频有效信息，得到更为精确的估计。

2 小波变换原理

2.1 根据小波变换构建模型

假设残差函数ξi(t)是一个包含噪声的一维信号，即ξi(t)可以表示为

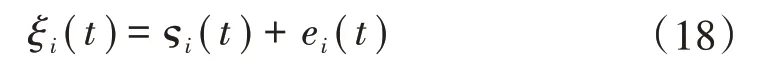
式中：ςi(t)为真实信号；ei(t)为噪声。将ξi(t)看成是一个闭区间上的有界连续函数，因此可进一步假设ξi(t)是平方可积的，根据离散小波变换的理论［16］，ξi(t)展开为

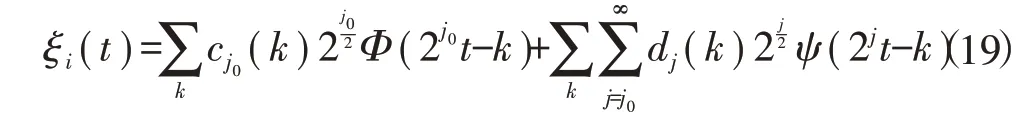
式中：Φ(t)和ψ(t)分别为尺度函数和小波基函数；cj0(k)和dj(k)分别为对应尺度下的系数。

由于实际应用中，得到的ξi(t)是一列离散的采样点，根据采样定理，尺度无法无限细分下去，因此具体计算中将ξi(t)展开为

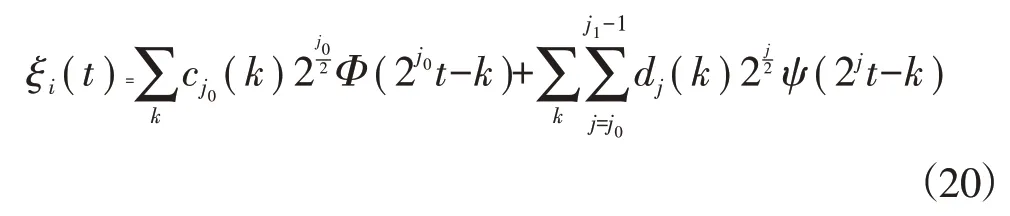
式中：j0=0；j1为分解层数。

2.2 去噪方案的选取

由于小波基、分解层数和阈值方案的选择会对去噪效果产生影响，对不同类型的数据可能需要选择不同的参数进行去噪，随机选取真实数据点中的10%作为测试集，根据不同参数组合在测试集上的表现选择最优的去噪方案。

可供 选择的 小波基［17-19］包 括db1-8、sym2-6、coif1-4，分解层数为1～8，阈值方案包括阈值选取规则和小于阈值小波系数的处理方法两个部分。

2.2.1 阈值选取规则

阈值选取规则主要包括四种方式：

1）无偏风险估计阈值（rigrsure），算法为：

b）若Aeta＜Acrit，则λheur=λsqt；若Aeta≥Acrit，则λheur=min{λrigr，λsqt}。

4）极大极小阈值（minimax）为

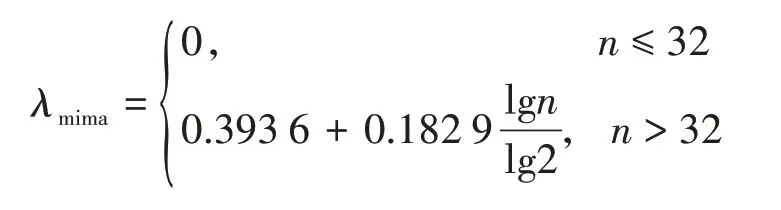
2.2.2 小于阈值小波系数的处理方法

小于阈值小波系数的处理方法主要包括两种：

1）硬阈值处理为

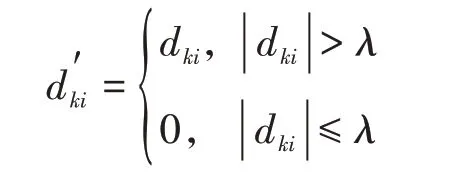
2）软阈值处理为

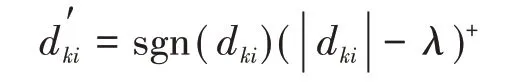
3 变压器运行数据缺失点修复方案

变压器运行数据缺失点修复方案主要包括三个部分，首先用FPCA方法得到观测对象的初次估计函数；然后估计残差函数，并用交叉验证的方法找到最优的小波去噪方案，得到对残差函数的估计；最后将残差函数的估计作为修正函数，与FPCA初次估计函数结合，得到观测对象在整个定义域中的估计值，用该估计值完成缺失点的修复。

以变压器第i天内某一类运行数据作为一个观测对象Yi，考虑连续n天内同一变电站的同一类数据，其中1 ≤d≤n。将第d天的观测对象Yd的真实观测值集合记为Sd={Yd1，Yd2，···，Ydnd}，nd为连续观测n天中的第d天，计算第d天的估计函数，包括9个步骤。

步骤1）随机选取其中10%的点作为测试集，记Ud={Ydt1，Ydt2，···，Ydtp}，p=[0.1×nd]，其 余90% 的点作为训练集，记为Vd={Ydtp+1，Ydtp+2，···，Ydtnd}。以第d天的训练集Vd，以及除第d天外所有的真实测量值作为训练集，用FPCA 方法建模，其中t的单位为分钟，考虑到实际情况，所有可能的观测点都是整数分钟。

步骤3）由式（6），得到s≠t时的协方差曲面的估计函数，再由式（11），得到s=t时协方差曲面的估计函数，从而得到整个协方差曲面的估计函数(s，t)。

步骤4）根据式（13），通过将协方差曲面离散化的方法，得到K组特征函数和对应的特征值的估计选取前k个最大的特征值及其对应的特征函数，使得式（14）定义的AFVE(k)大于给定的阈值θ。得到k个主成分的估计

步骤5）根据式（16），估计出观测对象Yd在主成分(t)上的得分。综合步骤1）—步骤5），得到对观测对象Yd的初次估计函数，即低频部分的估计为

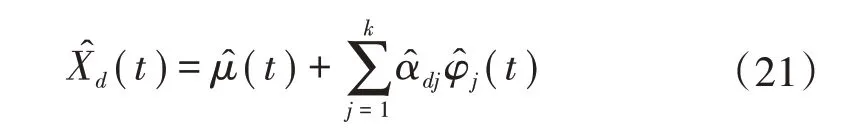
步骤6）估计残差函数(t)。为方便叙述，将前述Sd中的观测时间点记为，同理，记，tdnd}。当t∈时，则残差函数为当t∉时，补充定义td0=1，td(nd+1)=1440，则必存在p，使得t∈(tdp，td(p+1))。定义则当Agap较小时，可用移动平均来估计该点的残差函数的值，当Agap较大时，对残差函数的估计意义不大，反而可能造成最终估计的错误，因此直接置为零。综上，对残差函数(t)的估计为

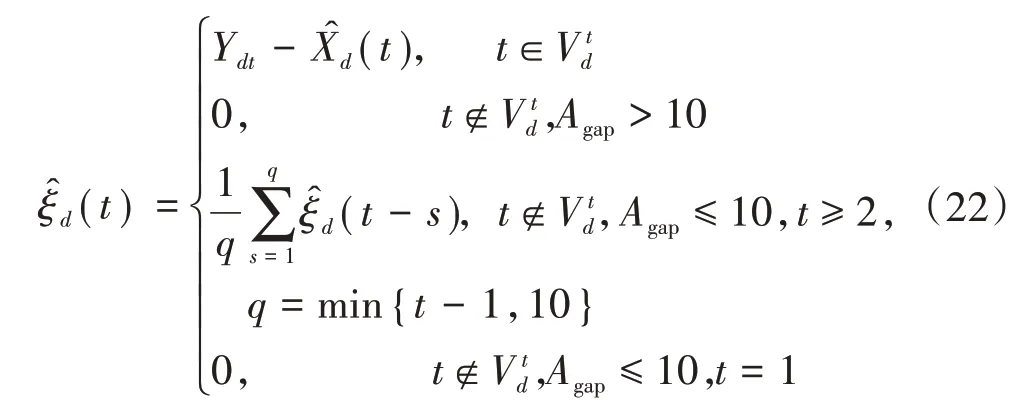
步骤7）利用MATLAB软件中的小波工具箱对残差函数进行小波变换，并选择最优的去噪方案。

首先选定一个去噪方案，用wden 函数进行小波去噪。该函数的四个参数“wname”、“n”、“tptr”、“sorh”分别对应于小波基、分解层数、阈值选取规则以及软硬阈值。最后一个参数“scal”表示定义的阈值是否需要重新调整，默认为“one”，即不用重新调整。输入去噪方案对应的参数以及信号(t)之后，就可得到去噪后的残差函数(t)。

选取不同的去噪方案，重复步骤7），记录最小的RRMSEi及对应的去噪方案。

步骤8）将训练集扩充为整个观测集，重复步骤1）—步骤5），更新初次估计函数(t)，再更新对残差函数(t)的估计。即用重复步骤6），得到更新后的残差函数为

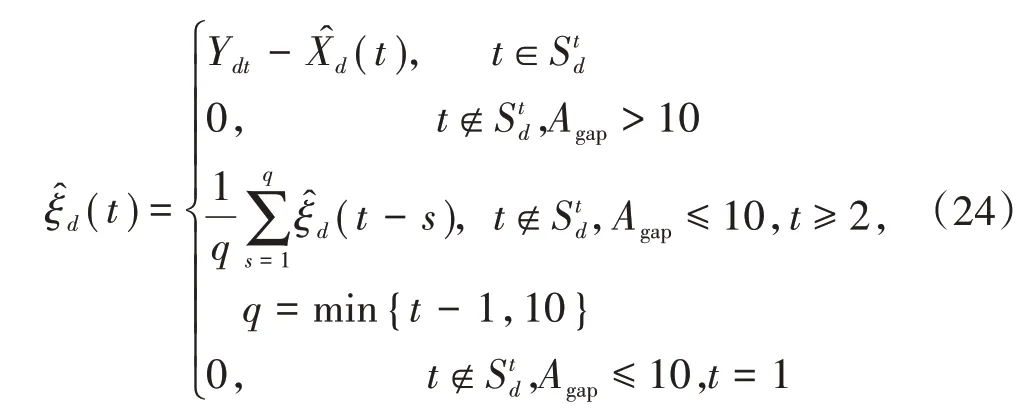
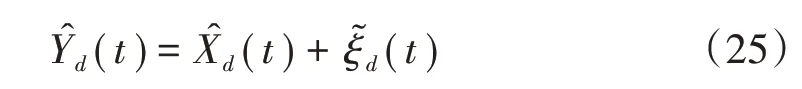
这样就完成了对观测对象Yd的修复。

4 算例分析

以某220 kV 主变压器某月的高压侧-I 数据为例，对本文所提缺失点修复方法进行测试。考虑到实际应用中既存在零散的随机缺失点，又存在连续缺失的情况，因此分别对这两种情况做了测试。

首先考虑缺失点零散分布的情况。以该月前十天的数据为例进行分析，1 日实际获取了997 个观测点，随机选取其中100 个点作为测试集，假设这些观测点缺失，以此为参照，评价修复效果。

经过步骤1）—步骤5）后，得到的初次估计函数如图1 所示。真实测量值及其变化趋势用黑点及黑色虚线连接，假设缺失的100 个点用蓝色星状点表示，初次估计函数用红色实线表示。

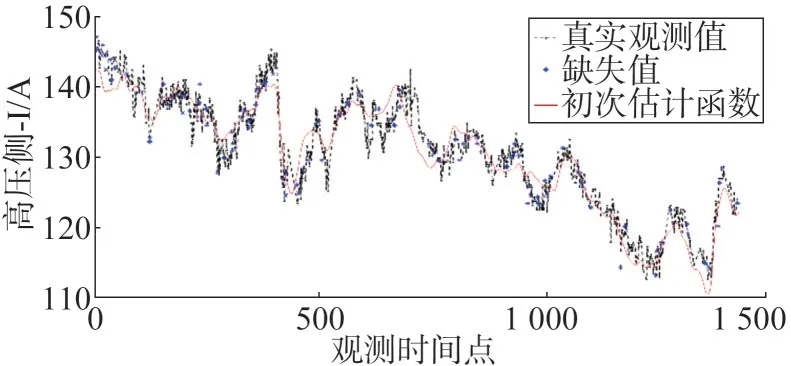
图1 初次估计函数

可以看到，初次估计函数已经能够较好地拟合真实观测值，但是在局部细节上还有欠缺。在步骤1）—步骤5）的基础上，继续实施步骤6）—9）后，得到的最终估计函数如图2 所示。黑点和蓝色星状点的含义同图1，红色实线表示最终估计函数。

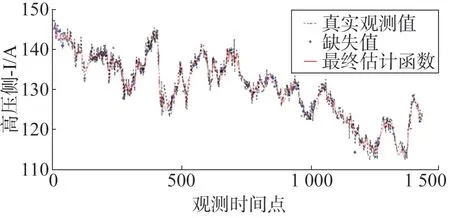
图2 最终估计函数

结果表明，在对初次估计函数加上修正函数之后，最终估计函数能够很好地拟合真实测量值。以测试集上的RRMSEd作为指标，将这种方法同三次样条插值方法进行对比。重复进行了10 次实验，每次的测试集都是随机选取，对比两种方法的均方根误差（Root Mean Squard Error，RMSE）如表1所示。

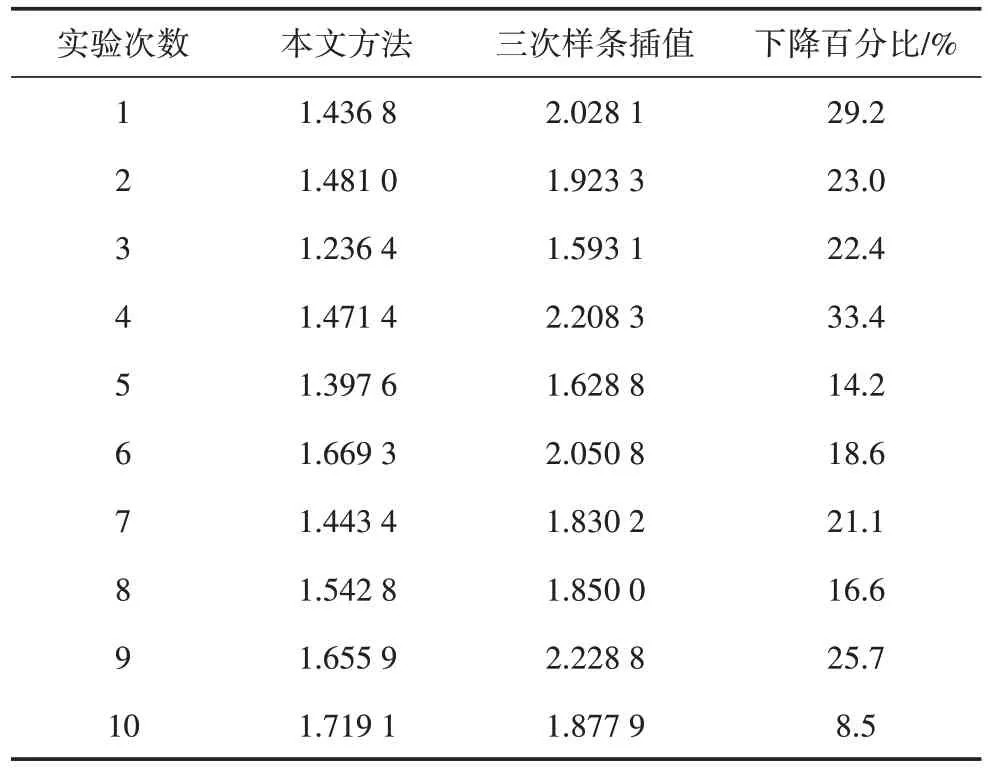
表1 高压侧-I上的RMSE对比

结果显示，经本文方法得出的估计函数在测试集上的RMSE 要明显小于三次样条插值法的RMSE，10次实验平均能够使RMSE下降21.3%，本文的缺失点修复方法更加稳定可靠。

当缺失点为大块的连续缺失时，普通的插值方法已经没法给出一个合理的估计，反而会添加错误数据。因此仍然以该月1 日至10 日的数据作为一组进行分析，假设第700～799 个观测值缺失，利用所述的方法，对该段的缺失值进行恢复。恢复的结果如图3所示。

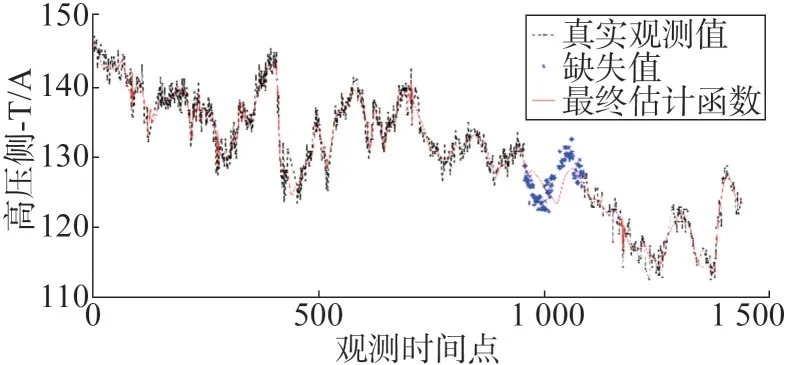
图3 连续缺失时的恢复曲线

为了检验在所考虑数据集上的整体效果，测试该方法应用于其他11 类数据上的效果，同高压侧-I的做法一样，随机选取100 个真实观测值作为测试集，重复实验10 次，分别计算本文方法和三次样条方法在测试集上的平均RMSE，结果如表2 所示。测试结果显示，本文方法在不同类型的变压器运行数据恢复上均有较好的表现。对三次样条差值方法有很大程度的提高。除高压侧-Q与中压侧-Q外，RMSE下降的百分比均超过15%。

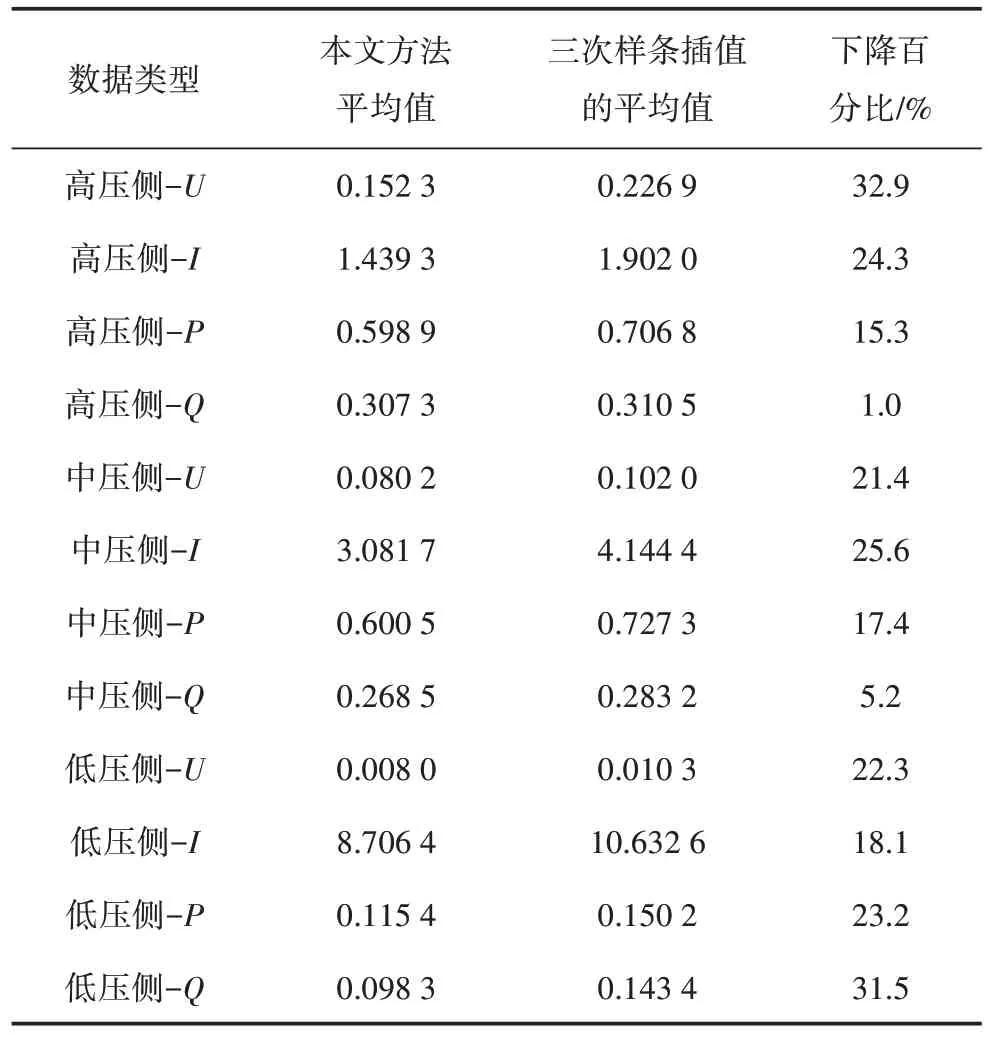
表2 12类数据上的RMSE对比

5 结语

利用FPCA 对数字信号整体特征的提取能力和小波变换对局部信息的提取能力，对变压器运行数据的缺失数据修复这一实际问题，提出了基于FPCA和小波变换的变压器运行数据缺失数据修复方法。

使用FPCA 方法能够实现对需修复数据集的初次估计函数；并利用交叉验证方法找到最优的小波去噪方案，得到对残差函数的估计；通过将残差函数的估计作为修正函数，与FPCA 初次估计函数结合，完成缺失点的修复。

该方法能够根据少量历史数据自动寻找数据的波动特征，并在此基础上对局部细节进行优化，从而完成对缺失数据的恢复。该方法对缺失点是连续分布还是离散分布没有要求，具有适用性广、恢复精度高的特点。