适用于核电厂BEPU的高效全局敏感性分析方法开发及应用

熊青文，苟军利，杜 鹏，邓 坚，邱志方，黄 涛，申亚欧

(1.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213；2.西安交通大学 核科学与技术学院，陕西 西安 710049)

近年来，随着世界核电技术的快速发展，核安全问题也愈加受到重视。2003年，国际原子能机构(IAEA)发表的报告总结了各种事故分析方法的分类，其将安全分析方法分为了4个选项，其中选项3，即使用最佳估算程序计算带有不确定性的真实输入数据的方法，也被称为最佳估算加不确定性(BEPU)分析方法，是目前核电安全分析的主流方法[1]。

BEPU方法中一个关键的步骤为参数的敏感性分析，其旨在评估输入参数对输出参数的影响大小。敏感性分析方法可根据其特征分为两类，即局部敏感性分析和全局敏感性分析[2]。局部敏感性分析的实现相对简单，对于简单的线性系统或单调系统，局部方法能用于评估输入参数的敏感性度量，但对于复杂的大型核反应堆系统，由于其存在高度非线性及参数间的相互作用，使用局部敏感性分析方法可能得到不充分的结果，因此发展全局敏感性分析方法很有必要。

常规用于工程应用的全局方法有基础效应方法、方差分解方法、矩独立方法等[3]。其中矩独立敏感性度量旨在评估输入参数对输出参数概率密度函数(PDF)的影响，通过计算输出参数的无条件PDF及固定一个输入参数的条件PDF之间的偏差值来评估输入参数对输出参数的影响。矩独立重要性测度由于其广泛的适用性而在近年来得到了大量工程应用[4-5]。

实际情况中应用矩独立方法最大的困难在于其需要大量的计算来估计输出参数的PDF，其计算过程涉及两个循环抽样计算，涉及的计算成本十分昂贵[6]。因此该方法往往被用于关系式模型或简单系统的敏感性分析，很难应用于核反应堆失水事故分析等大型复杂且计算耗时的工况。因此，如何降低计算成本是将矩独立全局敏感性分析方法应用至核电厂BEPU分析的一个重要课题。本研究开发一个优化的低成本全局矩独立敏感性分析方法，通过多个例题对其可靠性进行验证，并将其应用于LOFT(loss-of-fluid test)大破口失水事故(LBLOCA)的敏感性分析。

1 方法优化

矩独立全局敏感性分析方法旨在评估输入参数对目标输出PDF的影响。假设某个模型Y=g(X)存在k个输入参数，即X=(X1,X2,…,Xk)T，每个输入参数均服从一定的概率分布fXi(xi)，其不确定性可通过模型计算传播至输出Y。将Y的无条件PDF和累积分布函数(CDF)表示为fY(y)和FY(y)，将第i个输入参数Xi取某一固定值时得到的Y的条件PDF和CDF表示为fY|Xi(y)和FY|Xi(y)。根据定义，可将第i个输入参数的矩独立敏感性指标表示为：

(1)

其中，s(Xi)为固定第i个输入参数情况下输出PDF的偏移量，可表示为：

(2)

如上所示，由于计算参数的矩独立敏感性指标涉及到两个嵌套积分计算，且估计输出的PDF是一个不适定的问题[7]，因此总体的计算量十分巨大。传统方法的计算中总计算次数为R(kN1N2+N1)，其中N1为计算输出的PDF的抽样计算次数，推荐取值N1>1 000，N2为计算每个输入参数影响期望值所需的抽样计算次数，推荐取值N2>1 000，R为计算抽样样本方差所需的独立重复计算次数，由于大部分工程例题不存在解析解，因此对于传统方法，计算量越大，计算结果越精确。将求解输出的PDF转换为求解其CDF可在一定程度上优化计算结果。假设输出的fY(y)和fY|Xi(y)存在m个交点，表示为a1，a2，…，am，则s(Xi)可表示为m+1个子面积之和，即：

s(Xi)=s1+s2+…+sj+…+sm+sm+1

j=1,2,…,m+1

(3)

其中，fY(y)和fY|Xi(y)的交点和每个子面积sj可根据输出的FY(y)和FY|Xi(y)计算得到。为了能以十分小的计算成本且又相对精确地计算输入参数的敏感性指标，使用多种方法进行优化计算。首先，为降低积分计算的计算量，使用五点高斯求积方案替代积分计算[8]。基于高斯求积方案，可将矩独立敏感性指标表示为：

(4)

式中：ωi,j为第i个输入参数按照其分布类型确定的5个高斯权重值中的第j个值；Xi,j为第i个输入参数的第j个高斯点取值。ωi,j和Xi,j的取值与参数的分布类型及不确定性区间有关，具体取值可参考文献[8]。

求解s(Xi,j)的关键在于求解输出的条件和无条件CDF，即FY(y)和FY|Xi(y)。根据CDF的定义，可将其表示为：

FY(y)=P{Y≤y}=P{g(X)≤y}=

P{g(X)-y≤0}=P{z(X,y)≤0}=

Pf{z(X,y)}

(5)

其中：z(X,y)=g(X)-y为定义的新函数；Pf为失效概率。因此，可将求解模型g(X)的CDF转换为求解模型z(X,y)的失效概率，可根据四阶矩估计方法[9]和Pearson系统[10]来求解模型的失效概率。

由于采用五点高斯求积方案进行简化计算，因此每个参数仅需计算5个高斯点处对应的函数的输出值，同时还需计算一次参考点处对应的模型输出值，因此该方法需调用的模型计算次数最多为5k+1次。此外，对于不确定性分布服从正态分布、均匀分布或对数正态分布的参数，其每个参数仅需执行4次计算。

2 优化方法验证

为验证所提出优化的矩独立方法的准确性和适应性，本研究中将提出的优化矩独立方法应用至1个数值线性关系例题及两个工程非线性非单调例题，以验证该方法在简单线性系统及非线性非单调系统中的适应性。由于工程中大多数问题不存在矩独立指标的解析解，因此验证过程中使用基于双循环拉丁超立方抽样(LHS)的方法来求解矩独立敏感性指标的参考值，比较提出方法的计算值与参考值即可完成方法的验证。

2.1 数值例题

首先使用了一个数值例题来对双循环LHS方法和提出的方法进行验证[11]。该数值例题的表达式可表示为：

g(X)=1.5X1+1.6X2+1.7X3+

1.8X4+1.9X5+2.0X6

(6)

式中6个输入参数均服从标准正态分布N(0,1)。首先根据Borgonovo等[12]的工作可计算得到每个参数敏感性指标δi的解析解，而后使用双循环LHS方法和提出的方法分别执行1.201×109次和25次程序计算，如图1所示。此外，本算例中亦参考了其他作者的研究结果，图1中双循环MC和单循环MC是Wei等的计算结果[11]，两种方法的计算量分别为1.200 2×108次和6×104次。

图1 数值例题分析结果Fig.1 Result of analytical test

由图1可见，双循环方法由于使用了LHS方法，且计算量较多，因此相比于Wei等的计算结果，其结果更加接近于解析解。就数值而言，双循环LHS方法计算得到的敏感性指标相比于解析解相对误差在0.03%～0.24%之间，故双循环LHS方法的结果可作为参考解以验证优化方法的准确性。相对于双循环LHS方法，提出方法计算得到的矩独立度量误差范围在4.2%～6.4%之间，在计算量大幅减小的情况下依旧具有较高的计算精度。

双循环LHS方法和提出的优化方法计算结果间存在一个偏差，该偏差主要是由于使用高斯求积方案以及Pearson系统引入的。相对于敏感性指标δi的取值，该偏差相对较小，且其不影响参数的敏感性排序，因此提出方法的准确性可得到证明。

2.2 悬梁臂模型

悬梁臂模型是一个典型的结构力学问题，其经常被用于执行参数的敏感性分析，该模型的介绍可参考文献[11]。悬梁臂模型的表达式可表示为：

(7)

式中，参数X服从正态分布N(500, 402)，Y服从N(1 000, 802)，E服从N(2.9×107,2 320 0002)，w服从N(2.448 7,0.195 8962)，t服从N(3.888 4, 0.311 0722)，L服从N(100,82)。使用双循环LHS方法和提出的方法分别执行1.201×109次和25次程序计算，结果如图2所示。

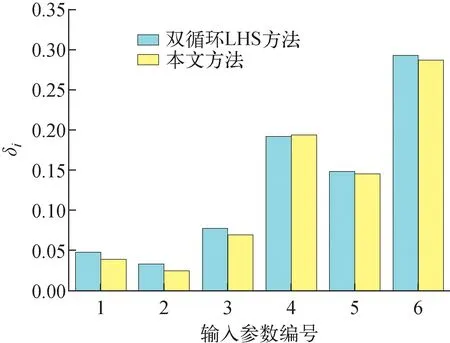
图2 悬梁臂模型分析结果Fig.2 Result of cantilever beam structure

验证结果显示两种方法结果十分接近，由于参数本身数值较小，因此计算得到的敏感性指标误差在1.15%～17.27%之间，且参数敏感性排序一致，进一步验证了优化方法的可靠性。

2.3 机翼重量函数

机翼重量函数旨在模拟计算轻型飞机的机翼重量，该问题也常被用于参数筛选的示例，其相关描述可参考文献[13]。机翼重量函数的函数表达式为：

(8)

式(8)中各变量的意义及分布列于表1，需要说明的是，由于不清楚参数的具体分布，因此假设所有参数均服从均匀分布。

表1 机翼重量函数输入参数及其分布Table 1 Input parameter and distribution of wing weight function

使用双循环LHS方法和提出的方法分别执行2.001×109次和41次程序计算，结果如图3所示。

图3 机翼重量函数分析结果Fig.3 Result of wing weight function

由图3可见，所提出优化方法的结果与双循环LHS方法的结果依旧十分接近，两种方法敏感性排序都是一致的。由于第2个参数对输出的影响小，因此基于降维方法计算得到的敏感性指标非常小，这是由于算法导致的，但不影响敏感性的排序。对于重要参数，优化方法计算得到的敏感性指标相比于LHS方法误差在0.8%～1.7%之间，由此可见，所提出的方法能以非常少的计算量，很好地估算出输入参数对输出的矩独立敏感性指标。

3 LOFT应用

如上所述，优化方法能以非常小的计算成本评估两个矩独立敏感性度量，且其在简单线性系统、非线性以及非单调系统中的适用性和准确性得到了评估和验证。为进一步验证优化方法是否适用于复杂的核反应堆系统，本研究中以LOFT装置LP-02-6 LBLOCA试验为对象开展了相关研究。

LOFT试验项目最早由美国NRC负责执行，后期成为由OECD成员国合作的国际化项目[14]。该试验项目探究了核反应堆在发生各种事故工况时的表现，其中以LOCA为主要分析对象。LOFT装置被设计为模拟典型四回路压水堆，是一个IET缩比试验装置，主要包括1个压力容器，1个用于模拟破口发生的破裂回路，1个包含有主泵、稳压器以及蒸汽发生器(SG)的完整回路，以及1个用于模拟安全壳收容作用的驰压容器。LOFT装置上开展了诸多试验，其中LP-02-6试验为模拟一回路冷管段双端断裂的LBLOCA，并模拟了失去厂外电源且只有1个ECCS投入使用的情况。

由于LBLOCA中最重要的验收准则参数为包壳峰值温度(PCT)，因此以PCT为目标输出，开展LP-02-6 LBLOCA中输入参数对PCT的矩独立敏感性度量计算。基于现象识别排序表(PIRT)筛选了15个重要输入参数[15]，这些参数及其不确定性分布列于表2。

表2 LOFT LP-02-6输入参数Table 2 Input parameter of LOFT LP-02-6 scenario

为验证提出的优化方法在核反应堆系统中的适用性，分别使用双循环LHS方法和优化方法执行了矩独立敏感性分析计算。其中，考虑到LOFT LP-02-6试验的模拟计算较为耗时，因此双循环LHS方法最终确定抽样次数为1.001×106，使用高性能服务器5个并行通道耗时约为1个月执行了这些计算。而对于优化方法，总计算次数仅为81，总计算耗时不到20 min。

双循环LHS方法和优化方法的计算结果如图4所示。

由计算结果可知，优化方法与双循环LHS方法的计算结果十分接近，对于重要参数，优化方法计算得到的敏感性指标相比于LHS方法误差在0.8%～31.4%之间，参数重要度排序亦高度相似，仅有3个重要度较小的参数敏感性排序不同，即衰变功率、稳压器水温和完整回路冷管段温度。因此，优化方法在计算影响较大参数的敏感性度量时相当准确，而对于影响较小的参数则可能存在一定的偏差，该计算精度可通过提高计算次数提高。考虑到核电厂事故中的敏感性分析主要目的在于确定工况中的重要参数，且考虑到诸多工况的单次模拟耗时较长，因此大多数情况下该优化方法能适用于核电厂的敏感性分析。

4 结论

针对局部敏感性分析方法原理不适用，而全局敏感性分析方法计算成本过大难以应用至核反应堆系统的问题，本研究以矩独立全局敏感性分析方法为对象，通过使用高斯求积方案、Pearson系统等方法开展了该方法的优化研究。研究中提出的优化方法的计算成本仅为输入参数数目的4～5倍，因此成本十分低，可被用于计算耗时的核反应堆系统的事故安全分析。

为验证优化方法的可靠性和适用性，首先使用一个简单线性系统以及悬梁臂模型、机翼重量函数两个非线性系统对其进行验证。为获得准确的参考解以评估优化方法的可靠性，本研究中使用了基于大量抽样计算的双循环LHS方法。通过对比双循环LHS方法和优化方法的计算结果，验证了优化方法在以上系统中的准确性和适用性。而后，使用LOFT LP-02-6 LBLOCA工况验证优化方法在核反应堆系统中的可靠性。通过对比双循环LHS方法和提出优化方法的计算结果，可得出优化方法能以十分小的计算成本准确识别工况中的重要参数的结论。