聚焦数学模型 提升科学思维
陕西 王昌魁
(作者单位:陕西省安康市石泉县石泉中学)
数学模型是发展学生科学思维重要的手段之一,其内涵是针对某种事物系统的特征或数量依存关系,采用数学语言,概括地或近似地表述的一种数学结构。因此,在高考的复习备考中,教师要立足静态的生物学表象,用深度的数学语言来引导学生升华自己的思维水平,推动学科之间的融合,实现冲刺阶段的“拔高训练”。这不仅仅是考试本身的要求,更是学科发展对学生综合素质的内在要求。下面笔者结合常见的数学模型图像分析题,谈谈相关理解。
生物学数学模型主要以各种函数图像呈现,因此对坐标曲线的分析显得尤为重要。借助生物学实验的描述,在各类知识板块中可根据自变量的数量、曲线的数量,将各类曲线图大致分为单曲线单自变量、单曲线多自变量、多曲线多自变量三种类型。上述曲线虽有多种,但在具体分析时也要遵循从简单到复杂、从单一到多数、从相同到不同的原则逐一展开分析。
1.单曲线单自变量分析
以常见的酶促反应速率曲线为例:
图1、图2均是单曲线单自变量变化曲线,在生物学基础考题中比较常见,相对而言这类曲线的分析比较简单,对曲线的分析一要准确认识自变量(X变量)和因变量(Y变量),二要看清走势并准确定位曲线拐点的真实含义。
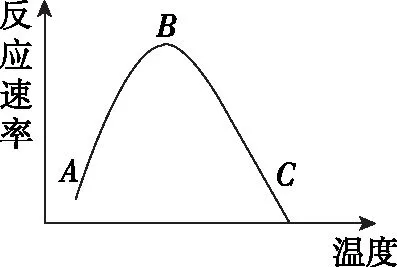
图1
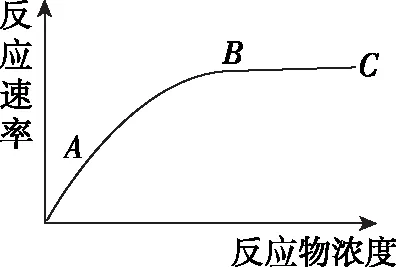
图2
图1自变量是温度,因变量是酶促反应速率。曲线先增长后下降的趋势说明温度对反应速率的影响是一个先升高后下降的过程,曲线变化过程中存在一个反应速率最大值B点,其对应的温度即为酶促反应的最适温度。由于酶的活性会受到温度的影响,因此本图很好地描述了温度通过影响酶活性来影响酶促反应速率,实验温度只要偏离最适温度就会使酶活性下降,从而使反应速率下降。
图2自变量是反应物浓度,因变量是酶促反应速率。曲线先增长后持平的趋势说明在AB段反应速率随着反应物浓度增大而增加,该段的限制性因素是反应物浓度,B点之后曲线持平,反应速率不再升高,说明反应物浓度不再是反应速率的限制性因素。探究其原因,是由于实验期间酶的浓度或者数量一定,必然存在饱和现象,因此,在酶饱和之后,反应物浓度就不足以升高酶促反应速率。B点后的限制性因素则为酶的浓度或数量。
2.单曲线多自变量分析
【例1】将某绿色植物放置在密闭透明的容器中,给予恒定且适宜的光照,在不同的温度条件下测定容器中CO2浓度的变化,结果如图3所示(该植物光合作用的最适温度为25℃,细胞呼吸的最适温度为30℃)。下列叙述错误的是 ( )
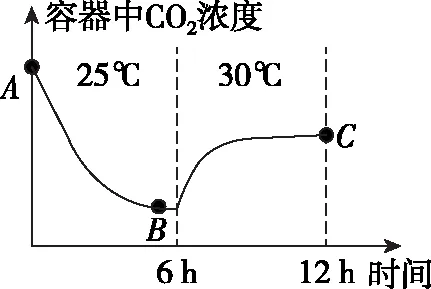
图3
A.从A点到B点的过程中,光合速率不断减小直至稳定
B.在B、C点时,限制光合速率的主要环境因素不同
C.与B点相比,C点时植株的光合速率变小
D.处理12 h后,该植物积累了少量的有机物
分析策略:单曲线多自变量图像稍显复杂,此类坐标图像题首先要提炼坐标图像要素,对这种多自变量的图像的分析,要注重“从果入手”,分区间讨论,尤其注重对斜率的分析,探寻内部生物学规律的实质变化,不仅要关注某一区间的变化,还要思考整体的曲线变化。
本题以时间变化、不同温度为自变量,容器中CO2浓度为因变量,在不同时段内分别用不同温度处理绿色植物,从而绘制出一条完整曲线。AB段实验温度为25℃(光合作用最适温度),曲线呈下降趋势,说明容器中CO2浓度降低,即光合作用速率大于呼吸作用速率,曲线斜率逐渐降低,说明二者之间的差距在减小。CO2作为光合作用原料,浓度的降低必然导致光合速率降低直至自身内部平衡,此时CO2浓度就会呈现先降低最终保持稳定的态势。
BC段实验温度为30℃(呼吸作用最适温度),曲线呈升高趋势,说明容器中CO2浓度升高,即呼吸作用速率大于光合作用速率,曲线斜率也在逐渐降低,同样也说明二者之间的差距在减小。O2浓度作为呼吸作用的原料,会因为呼吸作用的消耗而逐渐降低,最终必然导致呼吸速率降低至等于光合速率,此时CO2浓度会呈现先升高后保持稳定的态势。
B点和C点处曲线都呈现持平状态,说明均存在光合作用速率等于呼吸作用速率的情况,B点此刻限制性因素即为CO2浓度;同样是呈持平状态,C点却是先升高再持平,此刻限制性因素即为O2浓度。
B点和C点之间的光合速率大小比较,可以借用等量代换来理解。经分析得知:B点V(B光合)=V(B呼吸);C点V(C光合)=V(C呼吸);而30℃是呼吸作用最适温度,故V(C呼吸)>V(B呼吸),因此V(C光合)>V(B光合)。
C点纵坐标低于A点纵坐标,说明12 h后的CO2浓度相比实验初始降低了,CO2浓度变化作为光合作用和呼吸作用共同比较的结果,其浓度降低说明整体光合作用强度大于呼吸作用强度,减少的CO2被用于合成植物自身有机物。
3.多曲线多自变量分析
【例2】图4表示O2浓度和温度对洋葱根尖细胞有氧呼吸速率的影响。下列叙述错误的是 ( )
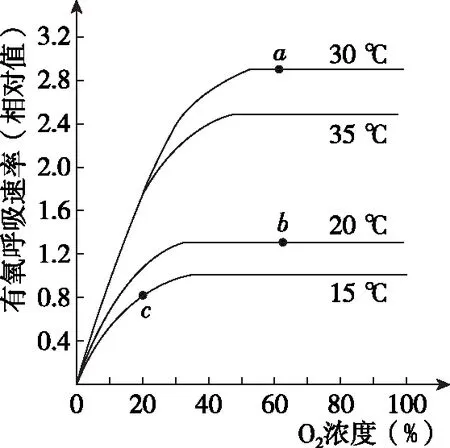
图4
A.与a点相比,b点与有氧呼吸相关酶的活性较低
B.与b点相比,限制c点有氧呼吸速率的因素有温度和氧气浓度
C.由图可知,细胞有氧呼吸的最适温度位于30℃和35℃之间
D.氧气浓度不变,a点时适当提高温度,细胞有氧呼吸速率可能增大
分析策略:对多曲线多自变量曲线图的分析仍然要建立在对单曲线的理解基础之上,教师要引导学生在识别单条曲线变化走势的基础之上,重点观察各曲线的相同或相似之处和不同之处,结合曲线差异分析内在原因,尤其是不同拐点所代表的深层次含义。
图4坐标图像中自变量是O2浓度和不同温度,因变量是有氧呼吸速率,以多条曲线表示不同温度之间的实验结果差异。各曲线的相似之处在于都表现出先升高再持平的大趋势,且各曲线在起始段都有一部分重合,说明在一定O2浓度下,有氧呼吸速率都随O2浓度升高而升高,该阶段O2浓度是曲线的限制性因素,而曲线持平则说明O2浓度不再是该阶段的限制性因素,即影响因素发生了变动。不同曲线拐点的差异同时体现在O2浓度和有氧呼吸速率值,说明在不同温度条件下,使有氧呼吸速率达到最大时所需的最小O2浓度各自不相同,再次揭示温度差异导致生理过程各方面产生差异。
制约有氧呼吸速率的因素很多,但教师要引导学生注意据图分析。在曲线持平阶段,相同的O2浓度却在不同温度下表现出不同的有氧呼吸速率,说明该阶段的限制性因素已经明确为不同温度。
温度通过影响酶活性进而影响有氧呼吸速率,a点有氧呼吸速率高于b点,所以a点酶活性高于b点。对于c点而言,横坐标对应的是20%的O2浓度,b点所处的20℃曲线高于c点所处的15℃,因此升高温度可以增大c点有氧呼吸速率,故温度是该点限制性因素,而c点正处于曲线升高阶段,升高O2浓度同样也可以增大有氧呼吸速率,限制性因素也包括O2浓度,故相对于b点,c点限制性因素为温度和O2浓度。曲线有氧呼吸速率最高值在30℃曲线上,故暂时只能认定30℃是最接近酶的最适温度,而最适温度区间则应选择20~35℃。有氧呼吸酶的最适温度不能确定,只能据图确定为20~35℃,因此氧气浓度不变时,适当提高a点温度,有可能增大细胞呼吸速率。
4.反思与启示
4.1数学模型有助于发展学生严密的思维逻辑
“科学思维”强调运用科学的思维方法认识事物,能够基于生物学事实阐释生命现象及规律。而利用数学模型描述生物学规律,可以很好地用数学原理推演进而把复杂多变的生物学规律呈现出来,从而使学生意识到生物学现象也“有章可循”,生物学现象的变化也要遵循一定的逻辑规律,这样才能使零散的生物学现象在严密的数学模型下以一种全新的姿态呈现在学生面前,故而在分析严密的数学模型时,教师可以进一步强化学生思维逻辑的严密性,同时在一定程度上提升了学生运用数学工具解决生物学问题的能力。
4.2数学模型有助于提升学生的审辩思维
在数学模型的建模、分析过程中,教师要引导学生从多角度分析曲线变化的表象,从而指导学生思考曲线变化的内在原因,要培养学生坚持探究事物真相、勇于思考和辨析的科学态度,同时学生也要从不同角度思考曲线变化的含义,质疑原有解释或者提出新解释,借助多方数据和合理证据,经过数理推演然后验证自我正确性。这个过程深化了学生的知识理解程度,尤其是对动态的生物学规律变化有了更深入的思考,同时也培养了学生去伪存真的科学态度和审辩思维。
4.3分析数学模型有助于提升学生的表达和沟通能力
生物学是一门实验科学,其学科特点要求学生既要掌握生物学一般规律,更要准确描述生物学的规律现象。通过对数学模型的集中探讨,不管是在学生自主分析、展示的过程中,还是在师生互动中,以及同学之间的协作讨论中,学生都需要组织合理、规范的生物学术语,借助严密的逻辑推演来表达自己的观点。学生通过交流沟通,既锻炼了表达能力,更使得头脑中的逻辑思维可以借助准确的语言文字表达出来,实现“心口合一”,提升了科学思维能力。

