一种纱线张力滑模模糊控制方法

王培良，叶秋阳，胡开亮，沈 刚

（湖州师范学院 工学院，浙江 湖州 313000）

0 引 言

纱线张力控制技术是纺织生产工艺流程中的重要环节，直接影响纱线的质量与生产效率。纱线张力的控制性能会直接影响纱线的成品质量。若纱线张力过小，则纱线容易松弛，导致脱圈，降低工作效率；若纱线张力过大，则纱线容易断裂，增加断头率［1］。因此，为了提高纱线质量，就要求纱线张力控制系统具有快速的动态响应速度和稳定的控制性能［2］。

针对纱线张力控制研究，许家忠等提出模糊控制结合变速积分PID控制的方法，提高了系统对参数变化的适应性［3］；赵学观等提出模糊自适应PID控制方法，使系统具有更好的动态稳定性和跟踪性能［4］；刘乐等提出了基于Hamilton理论的无张力计控制策略，保证了闭环系统的鲁棒稳定性［5］；康超等提出神经网络动态控制方法，对系统起到动态优化作用［6］；张楠等提出了基于BP神经网络的自适应PID技术控制纱线张力，提高了系统的响应速度与鲁棒性［7］。

滑模控制是一种变结构控制，具有鲁棒性强，对模型依赖性低，对参数变化及扰动不敏感以及物理实现简单等特点［8］。模糊控制是一种以模糊集合论、模糊语言变量及模糊逻辑推理为基础的计算机控制［9］，具有容错能力强，鲁棒性强和无需精确数学模型等特点。

本文针对纱线张力控制系统的非线性和实时性以及传统滑模控制存在的抖振幅值大和趋近速度慢等问题，结合模糊控制和滑模控制的优点，提出了一种基于改进多幂次趋近律的滑模模糊控制方法。该方法的输入可以是滑模面，有利于减少传统模糊控制的静差；模糊推理输出能柔化控制作用，削减传统滑模控制的抖振［10］。本文以无刷直流电机作为张力控制的执行机构，建立了纱线张力控制系统数学模型，改进了多幂次趋近律，设计了基于该趋近律的模糊滑模张力控制器。在MATLAB/Simulink环境中进行了仿真实验，证明了该方法的有效性。

1 控制系统数学建模

纱线张力控制系统结构如图1 所示。此系统由速度传感器、控制器、张力传感器、收卷机构和放卷机构5 部分组成。收、放卷机构分别由收、放卷电机和收、放卷辊组成。收、放卷电机分别拖动收、放卷辊，并分别与收、放卷辊直接相连。V2、V1分别为收、放卷辊线速度，l为收、放卷辊之间的纱线长度。当收、放卷辊之间存在速度差时，纱线内部就会产生张力。当V2大于V1过多时，会导致纱线张力过大，造成纱线断裂；反之，会导致纱线张力过小，造成纱线脱圈。如果可以将收、放卷辊之间的速度差控制在一定范围内，则能保证纱线张力稳定［11］。

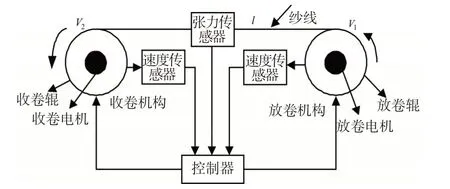
图1 纱线张力控制系统Fig.1 Yarn tension control system

无刷直流电动机（BLDCM）具有调速快速、运行稳定、精度高等特点［12］。因此，将无刷直流电动机作为张力控制系统的执行机构。简化BLDCM 的数学模型，则其三相绕组的电压平衡方程［13］为

式中：ua、ub、uc分别为定子绕组相电压；r为相电阻；ia、ib、ic分别为定子绕组相电流；ea、eb、ec分别为定子绕组电动势；L为每相绕组的自感；M为每两相绕组间互感；D为微分算子。

为了便于滑模控制器的设计，对式（1）加以简化。将整个电机当作一个整体，则BLDCM的电压平衡方程［13］为

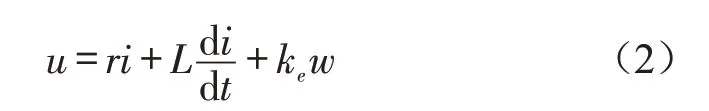
式中：u为电机端电压；i为相电流；r为相电阻；ke为反电势系数；w为电机角速度。

BLDCM的转矩平衡方程［13］为

式中：Te为电磁转矩，Te=kti，kt为转矩系数；TL为负载转矩；J为转动惯量；B为阻尼系数。

由式（2）、（3）以及文献［14］，可得电机端电压的表达式为

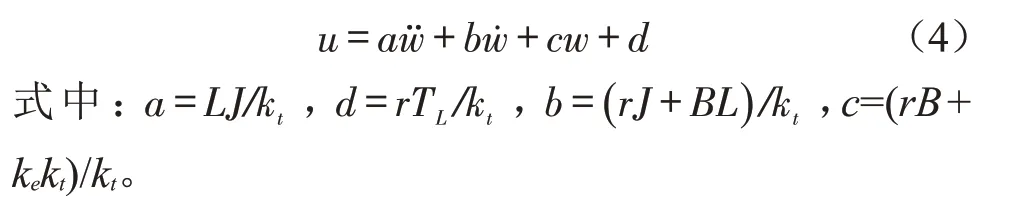
纱线在卷绕过程中，受力发生形变，纱线的应力表达式为

式中：σ为应力；E为弹性模量；ε为应变。

假设纱线的初始长度为l，形变后的长度为l0，则纱线的应变表达式［15］为

式中：V2为收卷辊线速度；V1为放卷辊线速度。

将纱线的弹性变形视为线性弹性变形，且忽略纱线形变前后密度与横截面积的变化，根据胡克定律，可得张力的表达式为

式中：F为纱线张力；A为纱线横截面积。假设放线速度V1恒定不变，在张力发生波动时，通过控制收线速度V2调节纱线张力，使其恢复到设定值［16］。

结合文献［17-18］，纱线张力控制过程如图2所示。

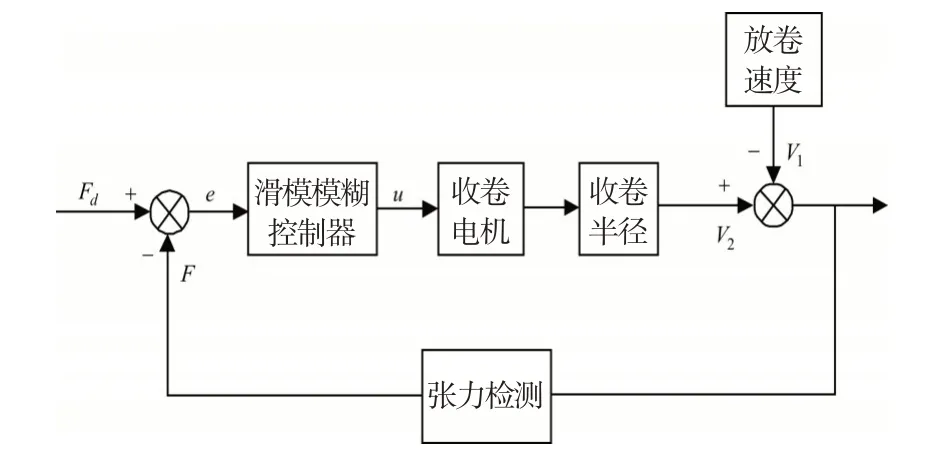
图2 纱线张力控制过程Fig.2 Yarn tension control process

根据式（4）和式（7），定义纱线张力控制系统数学模型的状态方程，即

式中：g=l/(AER)；h=d+cV1/R，R为收卷辊半径。

2 滑模模糊控制器设计

滑模控制包括系统从任意初始状态趋向滑模面的趋近运动和在滑模面上向平衡点运动的滑模运动2个阶段［19］。

2.1 滑模面

定义张力误差e为

式中：x1d为张力设定值。

根据纱线张力控制系统的数学模型，设计滑模面s，即

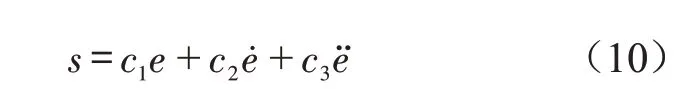
式中：s为滑模函数；c1、c2、c3均为滑模面的设计参数，且c1、c2、c3＞0。

2.2 趋近律

在滑模趋近运动过程中，采用趋近律的方法可以保证系统趋近运动的动态品质［20］。在文献［21］的基础上，将多幂次趋近律改进为

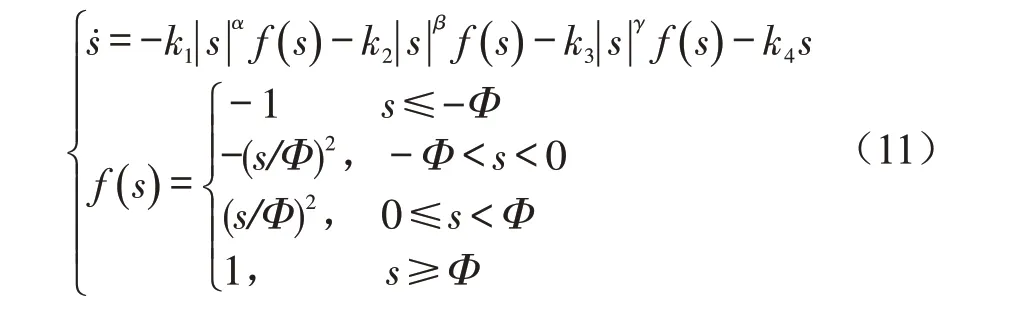
式中：k1、k2、k3、k4、α、β为趋近项系数；f(s)为边界层函数；Φ为函数f(s) 的边界层厚度；k1＞0 ，k2＞0 ，k3＞0 ，k4＞0 ，0＜α ＜1，1＜β，Φ ＞0。γ的取值采用模糊控制自适应调节，其表达式为

式中：γ0为γ的初始值；Δγ为模糊控制输出量。

在所提出的趋近律中，幂次项系数γ的大小会影响系统的收敛速度和抖振幅值。如果将γ设为定值，将很难适应张力控制系统的非线性、实时性及突发扰动。鉴于此，为实现对张力控制系统的最优滑模控制，设计一种模糊控制方法，根据实际情况来自适应调节参数γ。

2.3 滑模模糊控制器

滑模模糊控制器结构如图3 所示。滑模模糊控制器为两输入一输出，以滑模面s以及其变化率ṡ作为输入变量，以Δγ作为输出变量。通过模糊规则，实时调节趋近律参数Δγ，以适应不同时刻的控制需求。

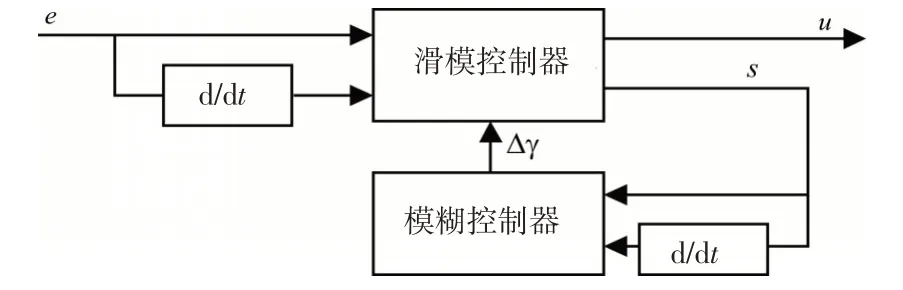
图3 滑模模糊控制器Fig.3 Sliding mode fuzzy controller

Δγ参数调节的模糊规则见表1，该模糊规则满足滑模控制的可达性条件s·ṡ＜0。当s、ṡ均为PB/NB时，要求Δγ为PB/NB，使系统以较大的速度降低s·ṡ的值；当s·ṡ＜0 时，系统满足可达性条件，有收敛于滑模面的趋势，则要求Δγ为ZE［10］。

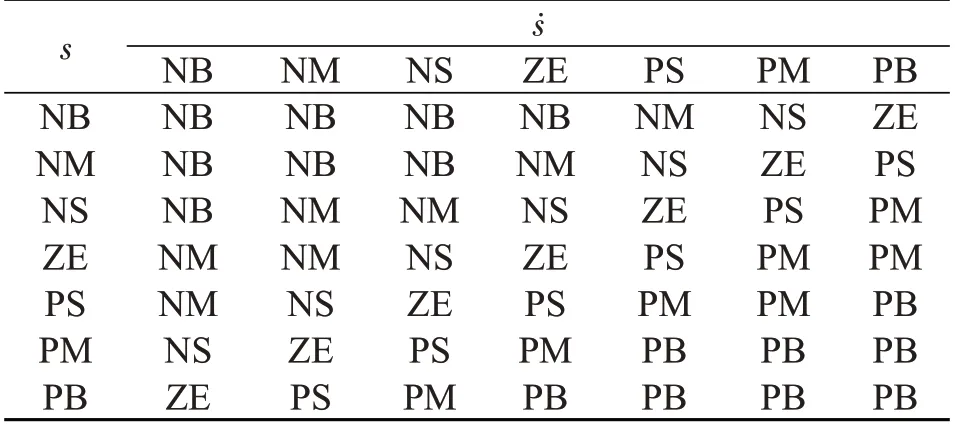
表1 Δγ 参数调节的模糊规则表Tab.1 Fuzzy rule table of parameter Δγ adjustment

模糊输入s隶属度函数如图4 所示，模糊输入ṡ隶属度函数与模糊输入s隶属度函数相同；模糊输出Δγ隶属度函数如图5所示。采用加权平均法对模糊输出Δγ进行逆模糊化。

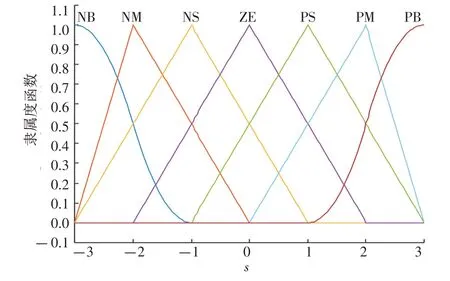
图4 模糊输入s 隶属度函数Fig.4 Membership function of Fuzzy input s

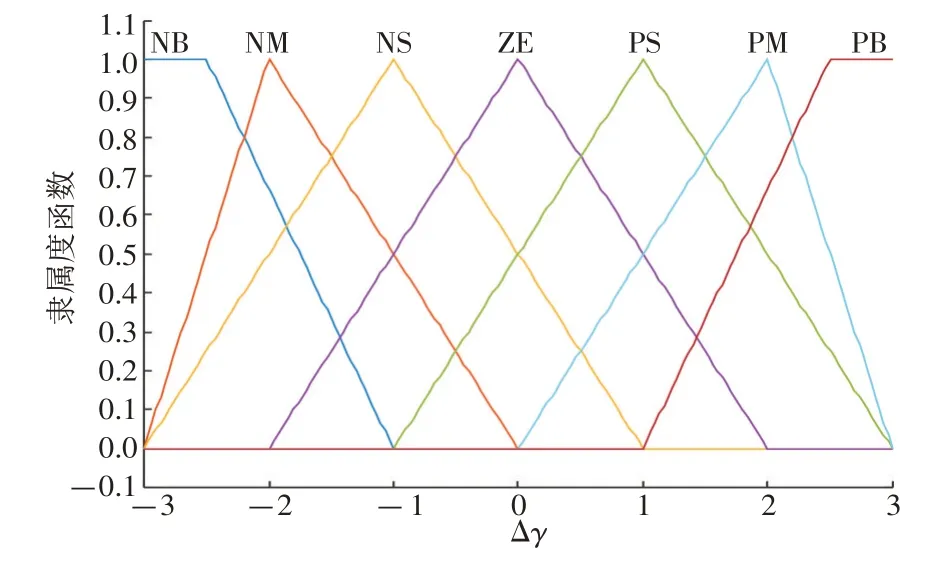
图5 模糊输出Δγ 隶属度函数Fig.5 Membership function of fuzzy input Δγ

根据式（8）、（10）和（11），设计滑模模糊控制器的控制律，即

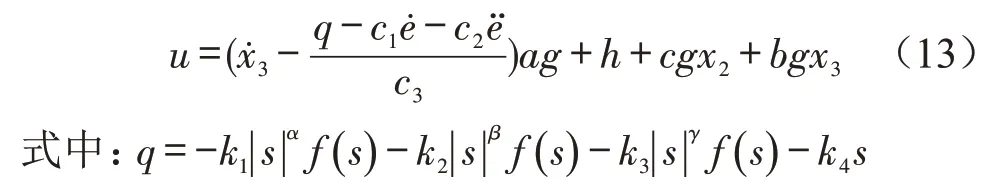
2.4 趋近律稳定性证明

通过李雅普诺夫稳定性定理证明趋近律的稳定性。选择李雅普诺夫函数为

根据式（14）～（16），可得V≥0 且V̇≤0 。当且仅当s=0 时，V=V̇=0。根据李雅普诺夫稳定性定理，可得所提出的趋近律满足稳定性条件，系统能在趋近律的作用下在有限时间内从任意初始状态到达滑模面。

3 仿真实验

为验证文中方法的有效性，以MATLAB/Simulink 软件作为仿真工具，分别采用指数趋近律（趋近律z1）、多幂次趋近律（趋近律z2）、文献［21］所示趋近律（趋近律z3）和文中所提出的趋近律（趋近律z4）设计控制律进行仿真对比，滑模面均采用式（10）的形式。为了便于表述，分别标记为控制方法1、2、3和4。

1）趋近律z1

2）趋近律z2

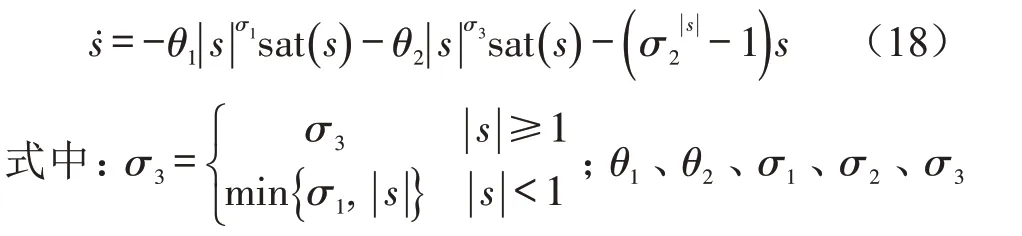
均为趋近律设计参数。

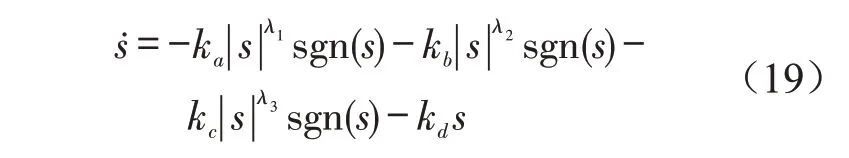
3）趋近律z3式中：ka、kb、kc、kd、λ1、λ2、λ3、λ4均为趋近律设计参数。

4）趋近律z4

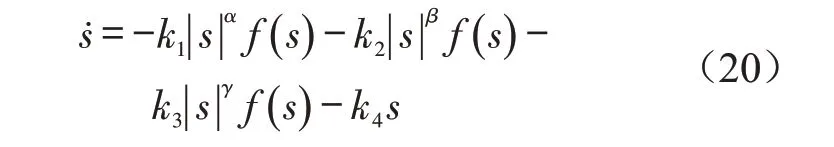
纱线张力控制系统仿真参数［13］中，相电阻r=1.32 Ω，相电感L为2.8×10－3H，阻尼系数B=6.59×10－6N·m，转动惯量J=1.57×10－5kg·m2，反电势系数ke=0.067 kg/m2，转矩系数kt=0.073 N·m/A，负载转矩TL=0.4 N·m，弹性模量E=1.74×1010Pa，纱线横截面积A= 3.14×10－8m2，纱线初始长度l=0.1 m。各趋近律设计参数如表2所示。

表2 各趋近律设计参数Tab.2 Parameters of each approach law

图6、7分别是不同控制方法下s、ṡ变化曲线。

图6 不同控制方法下s的变化Fig.6 The change of s under different control methods

由图6和图7可知：各个控制方法下的系统到达滑模面的时间分别为0.922、0.906、0.610 和0.440 s；控制方法4下系统的收敛时间最短，相对于其他控制方法时间上相对缩短了52.3%、51.4%和27.9%。控制方法2和控制方法1下的系统在一定范围内滑动，产生了抖振现象。控制方法3 和控制方法4 下的系统到达滑模面后，基本没有产生抖振现象，控制方法4降低抖振更为有效。

图7 不同控制方法下ṡ的变化Fig.7 The change of ṡunder different control methods

图8 是模糊控制器输出变量Δγ变化曲线。分析图8 可知：Δγ随着时间先下降至－1.96 后快速上升至1.96，最后下降至稳定状态。当系统未到达滑模面之前，模糊控制器输出Δγ根据s以及ṡ自适应调整，用以提高收敛速度；当系统到达滑模面时，模糊控制器输出Δγ趋于稳定，用以降低滑模运动的抖振。

图8 模糊控制器输出变量ΔγFig.8 The change curve of output Δγ of fuzzy controller

图9、图10 分别是不同控制方法下的控制器输出信号u、纱线张力F响应变化曲线。分析图9 可知：4种控制方法下的控制器输出到达稳定状态的时间分别为2.047、1.919、1.817 和1.416 s。控制方法4所需的时间最短，率先趋于稳定状态，相对其他3 种方法时间上分别缩短了30.8%、26.2%和22.1%。控制方法1和2下的控制器输出信号趋于稳定时，存在一定范围内波动。

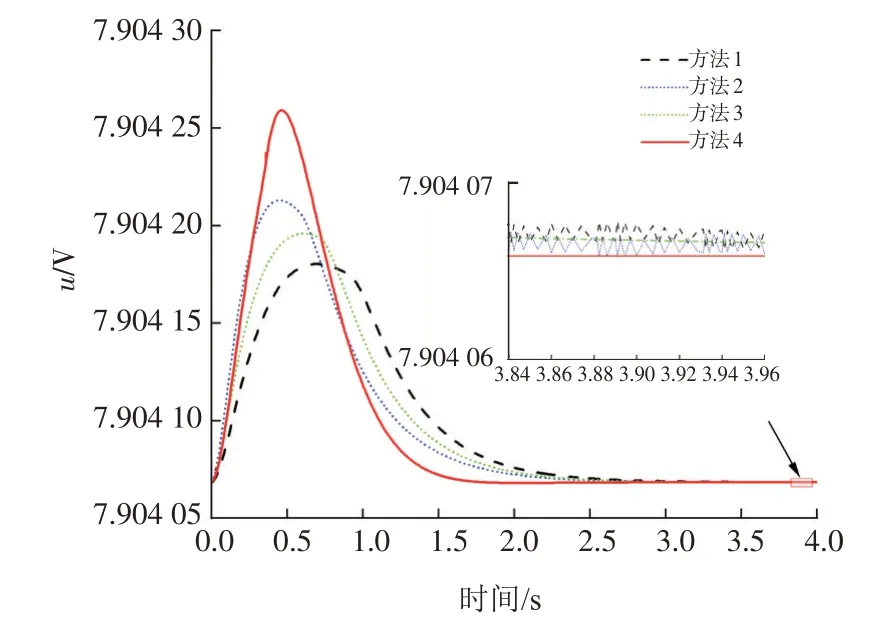
图9 不同控制方法下的控制器输出信号uFig.9 The change curve of output signal u under different control methods

分析图10 可知：4 种控制方法下的纱线张力输出值到达张力设定值的时间分别为2.337、2.198、2.094 和1.575 s，控制方法4 相对其他3 种方法时间上分别缩短了32.6%、28.3%和24.8%；纱线张力响应较快，纱线张力输出值率先达到了张力设定值。在0～0.4 s 期间，控制方法4 的纱线张力低于方法2。但是，在此期间，Δγ的自适应整定不断地提升控制方法4 的收敛速度；0.4 s 之后，控制方法4 的纱线张力超过了控制方法2，直至进入稳定状态。

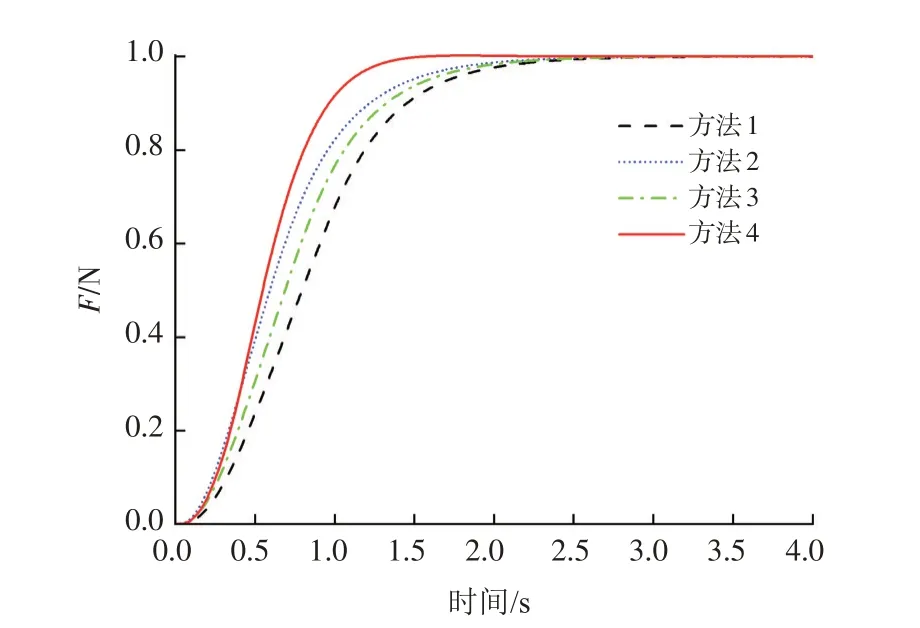
图10 不同控制方法下的纱线张力F 响应Fig.10 The change curve of yarn tension F response under different control methods

仿真结果证明了所提出方法的有效性，不仅提高了收敛速度，还降低了抖振。纱线张力控制系统的张力输出响应速度和控制器输出信号稳定性得到了提高。

4 结 语

针对传统滑模控制收敛速度慢、抖振导致的纱线张力控制系统输出响应速度慢、控制器输出波动大的问题，提出一种基于改进多幂次趋近律的滑模模糊控制方法。通过对纱线张力控制系统的数学建模以及仿真，验证了该方法的可行性与有效性。基于该方法的纱线张力控制系统不仅能有效降低系统抖振，还能提高收敛速度；能快速响应指令输入，且提升了输出信号的稳定性，具有较好的控制性能。