非线性对流反应扩散方程爆破解的B方法

李智杰，王 妍

（西安建筑科技大学 理学院，陕西 西安 710055）

0 引 言

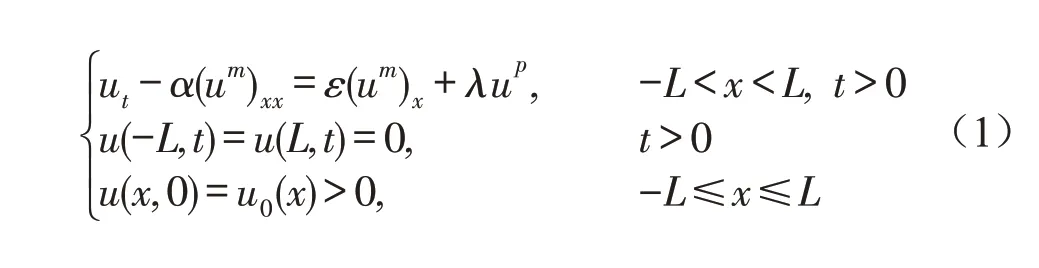
考虑如下完全非线性反应扩散方程的爆破问题，其中α,ε,λ ＞0 ，p＞m≥1，L为正常数，初值u0(x)满足

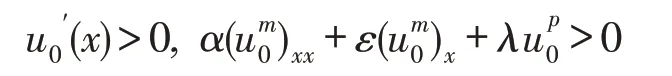
完全非线性系统作为一种重要的物理模型，常用于描述复杂介质的流动问题，如超变形核、液滴裂变以及惯性聚变等［1］。1950 年，Zeldovich 和Kompaneets 提出了一种非线性多孔介质方程ut=α(um)xx，用于描述绝热气体在多孔介质中的流动过程。例如，当m=2 时，对应水文学中的Boussinesq方程的无量纲重构［2］。此后，含有源项λup及对流项ε(un)x的多孔介质方程相继被提出。例如，液滴模型中的B(n,n)方程即为后者在n=m时的特殊形式［3-4］，而当n≠m时，则通常表示泡沫排水方程［5］或斜板上薄黏性液体运动的过程［6］等。

此后，由于研究实际物理模型的需要，一类能够描述复杂多孔介质间作用系统的方程

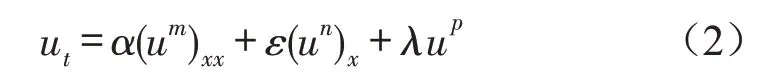
开始被关注［7-8］。该方程（2）的各个参数α、ε、λ、m、n以及p在不同组合下，可以涵盖大量非线性抛物问题相关的数学模型，并且该方程的一些退化形式已有大量研究[9-14]。此外，由于当p＜m时方程（2）已被证明其所有解都一致有界［15］，因此，目前的研究大都集中于p＞m的情形。

处理非线性奇异问题的数值方法有局部加密、多步格式［16］、自适应移动网格［17］等。由于爆破点附近解趋于无穷大，一些传统的数值方法不能精确地模拟爆破点附近解的渐近行为，因而估计的爆破时间会偏离真正的爆破时间，尤其是考虑到问题（1）中还存在对流项对解产生的复杂影响［18］。因此，需要一种能够精确模拟爆破点附近解的渐近行为，同时能降低运算复杂度的数值方法。B方法作为一种兼顾以上需求的时间半离散数值方法，其构造思想由LE ROUX 于1992 年首先提出。在实际问题中，许多爆破模型通常由一个非线性源项和一个扩散项2部分组成，而且非线性项是造成爆破的主要原因，扩散项只是延迟了爆破发生的时间。前者对解的扰动较后者占优，且越临近爆破发生时越明显。因此，为使数值解能够在追踪爆破时间时具有更高的精度，LE ROUX 等首先将方程变为没有空间算子的演化方程的形式，即仅考虑对爆破过程起重要作用的非线性常微分方程，并求出该方程的精确解。之后，再对这一非线性常微分方程进行离散并将空间算子回填，最终得到一种能够保持解的几何结构的数值方法。考虑到该方法对爆破解具有极好的逼近特性，故以爆破（blow-up）的英文首字母命名，称作B方法。

LE ROUX等于1994年完善了B方法的相关理论之后，利用B方法在1998年和1999年研究等离子体物理学中一类带有高阶源项的非线性扩散方程的爆破问题［19，20］，给出了解在有限时间内爆破的理论依据，证明了数值解的渐近性与收敛性，并于2000 年验证了B 方法在该方程高维情况下的适用性［21］。2009 年，LE ROUX 又利用B 方法研究方程组解的渐近行为［22］，得到了爆破时间的估计以及数值爆破解的收敛性。2015年，BECK等进一步发展了LE ROUX 的理论，使用B 方法研究拟线性抛物方程（组）及半线性波动方程的爆破问题［23］。2018年，霍冠泽等将B方法用在处理一类抛物方程的猝灭问题上［24］，证明了数值解的存在性并通过算例验证了B 方法在求解方程猝灭解时的有效性。2020年，霍冠泽等又使用B 方法研究了一类四阶抛物方程的爆破问题［25］，展示B 方法在处理该类问题时的优势。

由此可见，利用B 方法研究微分方程的奇异问题，尤其是爆破问题时确实能够得到非常好的效果。不过，以上问题都围绕只包含拉普拉斯算子及非线性反应项的方程（组）展开，对含有对流项的问题研究较少；而且含有对流项的方程没有变分结构，故之前文献所使用的能量泛函方法也将不再适用。本文通过构造辅助函数方法证明问题（1）的解在有限时间内爆破理论，即通过对应椭圆方程的特征函数定义新的检验函数，并证明其满足一个常微分方程不等式。本文中还给出了问题（1）B方法数值格式的具体构造过程及其收敛性、数值解存在性的证明和爆破时间估计。通过数值算例验证相关结果的正确性，并将B 方法与3 种传统数值格式在不同区间长度下的模拟结果相比较，展示了B方法在处理相关问题时的优势。同时，算例也刻画了对流项及对流系数对于数值解爆破过程的影响。

1 方程解的渐近行为

首先给出问题（1）的解能够发生爆破的充分条件。在区域[-L,L]引入Laplace 算子的线性特征值问题

成立，并由此可知问题（1）的解会在有限时间内爆破。

2 B方法数值格式及其数值解性质

定理2［27］若带有Dirichlet边值条件的椭圆问题Lv=f(x,v,∇v)满足：

（i）非线性项f(x,v,∇v)关于∇v至多是二次增长的，即存在函数h(x,v)关于x∈[-L,L]可测，关于v连续，以及函数H(x,v,vx)关于其自变量均连续，使得f能够被表示为

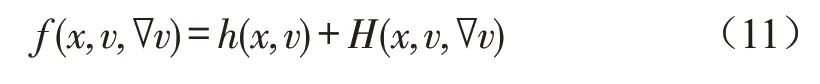
3 构造全离散数值格式

由于隐格式（7）的全离散格式难以直接计算，因此需要寻找它的一个逼近序列，并证明在第n层给定迭代首项的情况下，该序列能够经过有限次迭代之后收敛到第n+1层。根据文献［28］的结论，若

4）生成采样坐标对，绘制函数图像。

利用B方法及有限差分方法构造了全离散数值格式。值得注意的是，在选取空间差分方式时有多种选择，此处选择有限差分方法，是由于其所对应的迭代矩阵相对简洁，在利用计算机进行数值模拟时可以大幅缩减计算时间。另外，可以根据不同的需求对空间离散方法进行调整，以满足不同类型的实际模型。

4 算例

以一维非线性对流反应扩散方程为例，采用所构造的格式进行模拟，并与3 种传统数值格式的计算结果比较，验证本文数值格式在处理爆破问题时的精确性及可靠性。

固 定 参 数α=0.1 ，ε=0.3 ，λ=2 ，m=3 ，p=6，讨论随着区域范围的变化，4种格式相应的数值模拟情况。令u(x,t)为待求未知量，得到方程及其初边值条件如下：

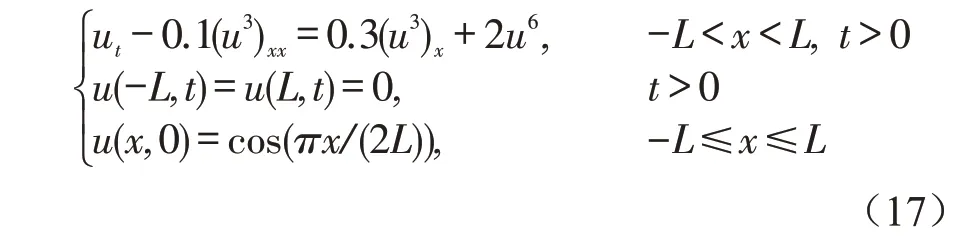
如前所述，随着时间推移，方程（17）的解将在有限时间内出现爆破现象。选择了4 种数值格式模拟问题（17）解的爆破过程，分别为B 方法、切比雪夫谱方法、有限差分法及4-5 阶龙格库塔法。空间步长统一取作Δx=0.01，并选取T=0.23 作为数值爆破时间进行观察。这样既能够保证刻画解在t时刻附近爆破现象，又不会因为过于靠近实际爆破时间而使得模拟失真。首先以L=1/2 为例，展示爆破发生前，4 种格式数值解随时间变化的过程。其中有限差分法对应数值解的爆破现象发生过早，此时将爆破时间取为T=4×10-4，即解出现奇性的前一刻。给定参数下不同算法的模拟结果如图1所示。

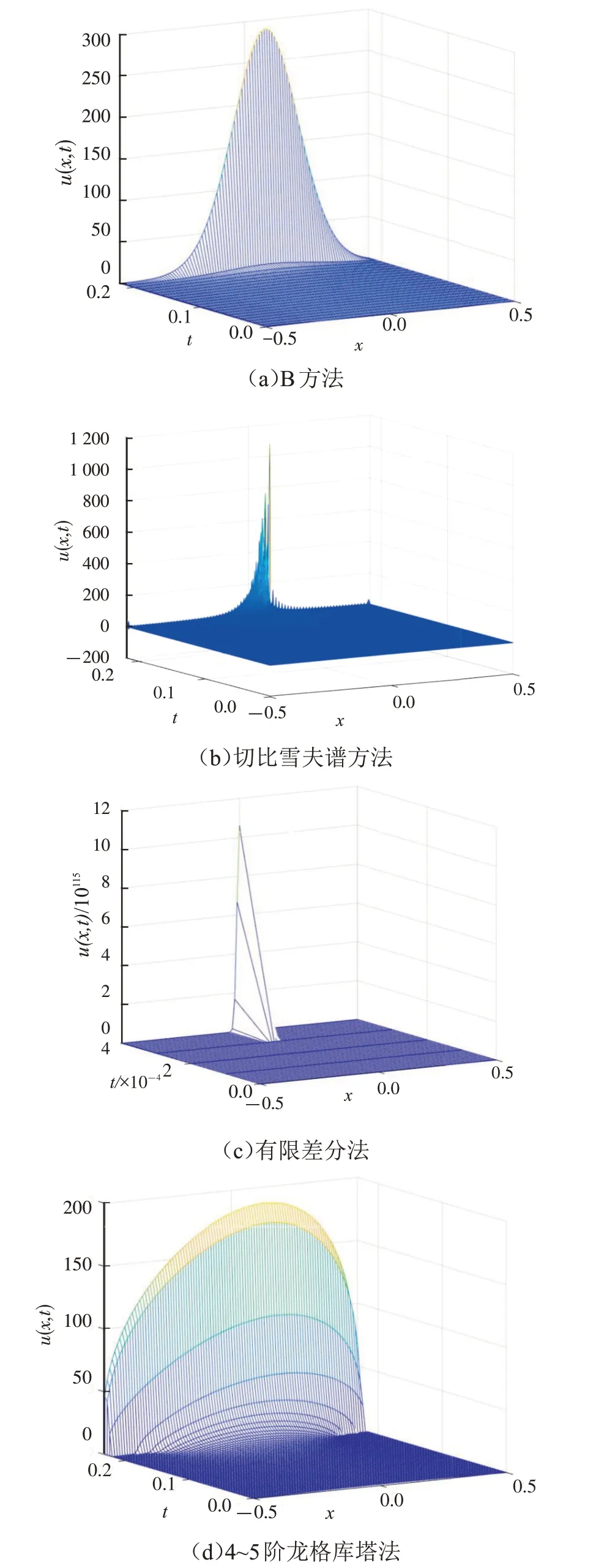
图1 给定参数下不同算法的模拟结果Fig.1 Simulation results of different algorithms under given parameters

从图1 可以看到：在临近爆破点时，B 方法依旧能够保持解的光滑性，而切比雪夫谱方法对应解则产生较大的震荡；有限差分法在T时刻之后产生了奇性，以至于计算机在模拟时会由于部分结点震荡过大而出现严重的网格间断。4～5 阶龙格库塔法虽然能够保证解的光滑性，但爆破过程中数值解出现的形变较为严重，爆破点位置也有较大偏差。可见，B方法在模拟数值解爆破过程的精确度方面更具优势。

对问题所在区域进行调整，分别取L=1/2 、π/4、π/2、2，并将4种算法在对应爆破时刻数值解的形状通过等比例压缩至相同的坐标区间，以便更为直观的比较区间长度的变化对各算法数值解带来的影响，结果如图2 所示。由图2 可以看到：随着区间长度的增加，B方法的空间结点分布依旧均匀，曲线平滑，同时方程爆破点位置的偏移现象也刻画的较为准确；切比雪夫谱方法虽然获得了与B 方法相近的爆破点，但由于数值解本身的剧烈震荡，且在爆破发生时数值解不恒为正，使得数值解与理论结果不符；有限差分法由于误差较大，导致仅仅在非常短的时间之内，数值解便出现奇性且爆破位置偏差严重；4～5阶龙格库塔法数值解虽然光滑，但行波迎风面结点分布不均，爆破位置同样偏差较大，刻画不准确，并且这一现象随着L的增大逐渐明显。

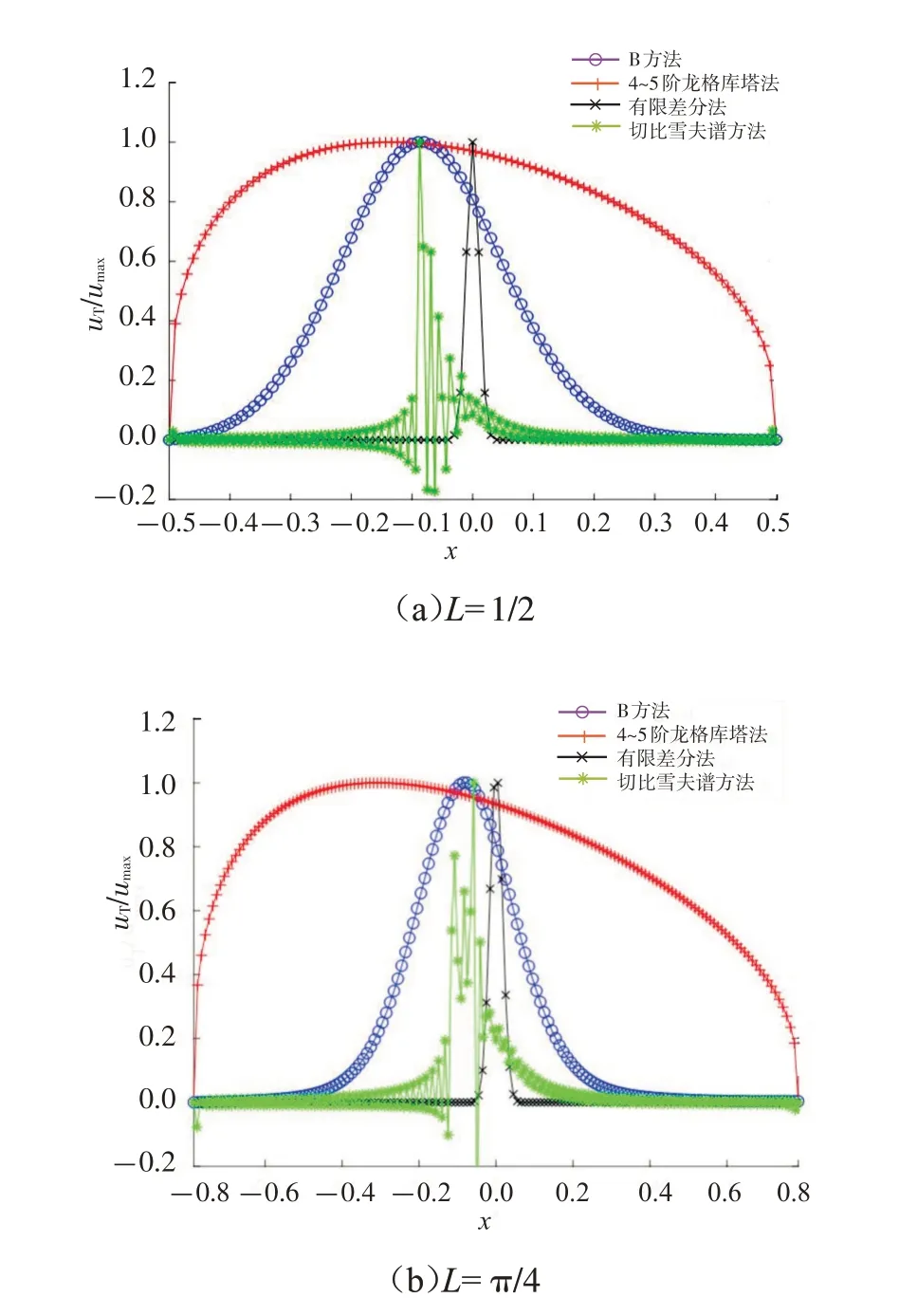
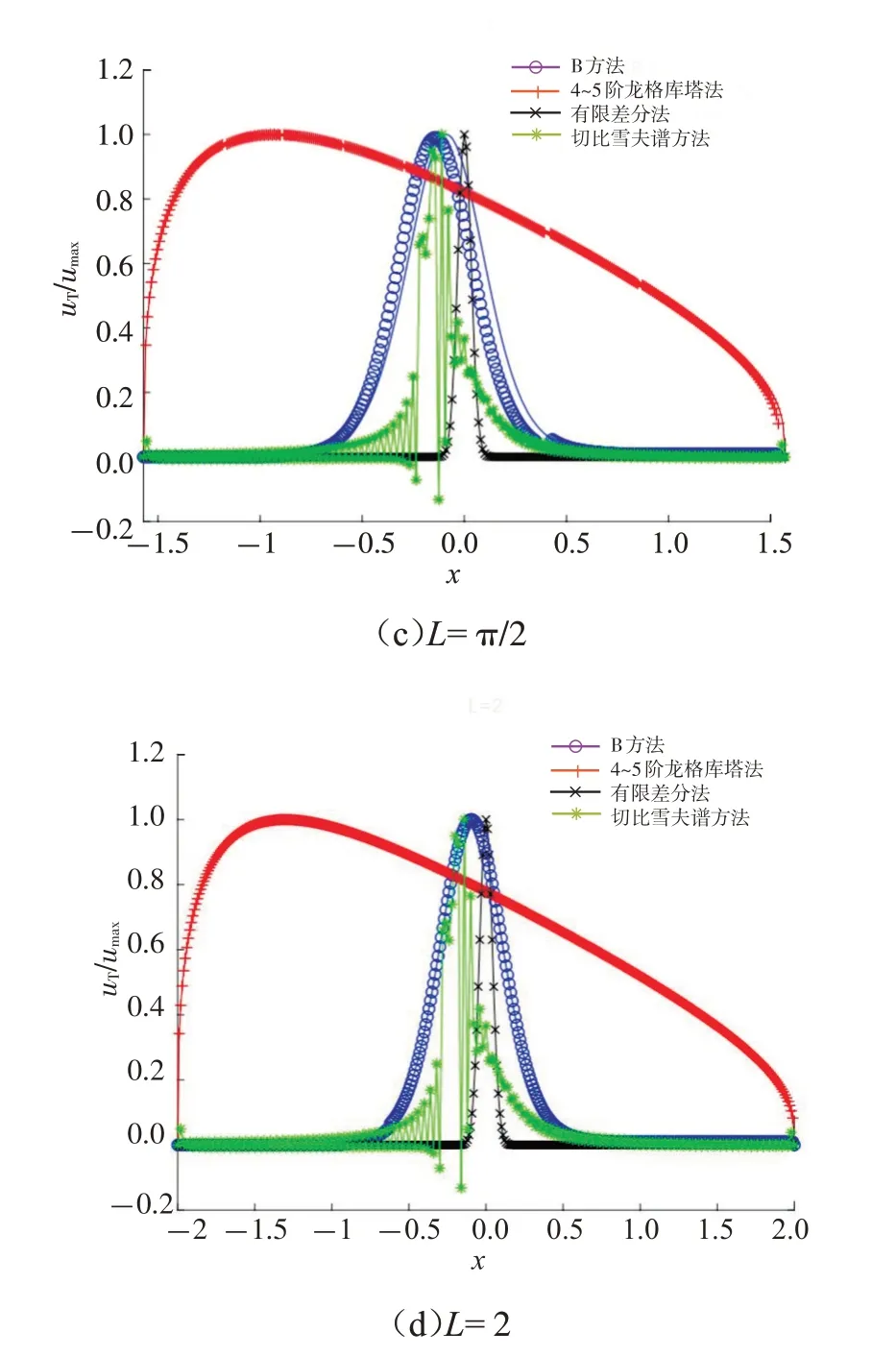
图2 不同区间长度下4种格式模拟结果Fig.2 Simulation results of four formats under different interval lengths

以B 方法在L=1/2 ，T=0.2 时刻的模拟结果为例。图3 展示了取不同的对流项系数时，随着ε增大，对流项所产生的阻尼效果越来越强的物理现象。当ε逐渐变大，对流效果愈加明显的同时，同一时刻数值解的最大值也在相应地减小。可见，ε对该问题解的影响与其物理意义保持一致。

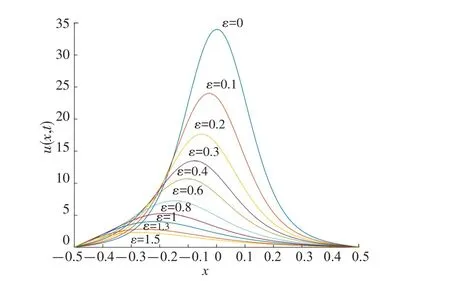
图3 不同对流系数对数值解的影响Fig.3 The influence of different convection coefficients on numerical solution

此外，B方法在利用计算机进行模拟时，相较于其他算法具有更高的性价比。表1 给出了上述4 种格式相应程序的运行情况。表1中：运行时间为同一设备在相同状态下，各程序运行10次所用的平均时间；函数调用次数为包括主函数、子函数及嵌套函数等在内的总调用次数；网格密度为单位面积内的平均网格数。实验设备为一台搭载2.6 GHz Intel Core i7-10750H处理器，内存为16 GiB的笔记本电脑。

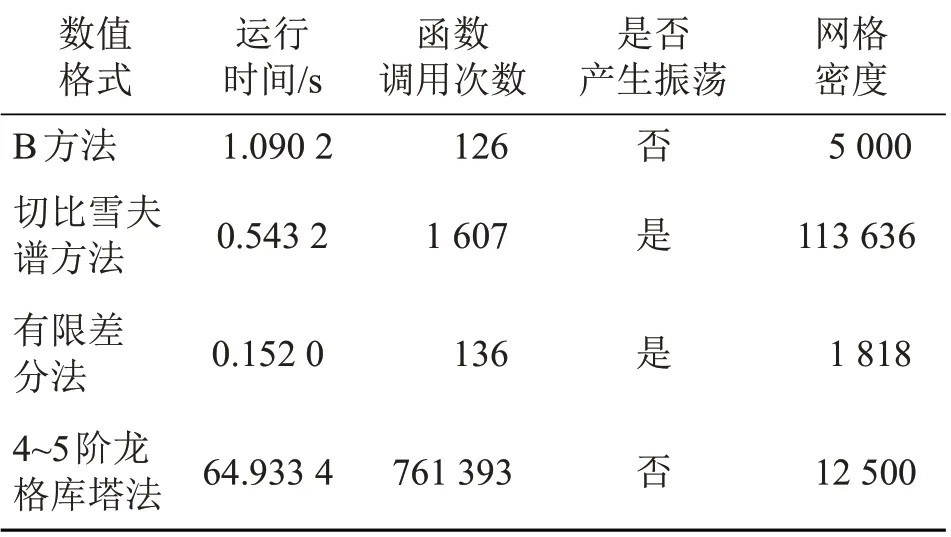
表1 各数值格式运行情况Tab.1 Operating information in various formats

通过表1可以看出：与B方法相比，切比雪夫谱方法虽然计算时间较短，但调用函数次数较多，网格密度大且产生震荡现象，因此可以考虑用来确定爆破点的位置，但不适合模拟爆破问题的数值结果。有限差分法虽然计算时间最短，函数调用次数较少且网格密度小，但结合图1、2 来看，其精度最低，误差最大；4～5阶龙格库塔法虽然未产生震荡且网格密度适中，但函数总调用次数过多，程序遍历时间过长，运算效率低下；B 方法虽然计算时间略长，但函数总调用次数最少，即使在低性能计算机上运行也能够保证计算效率，因此更适用于模拟此类含奇异解的非线性方程。

5 结 语

得益于B 方法对数值解奇异行为的控制，该方法在处理非线性对流扩散方程的爆破问题时有非常好的表现，使得其能够在较短时间内，准确地模拟解的爆破行为。同时，该方法用空间换时间，提升了对运行内存的利用率，是目前利用计算机模拟非线性微分方程爆破问题有力的工具之一。但B方法作为一种时间上半离散格式，在构造全离散格式的过程中，有时仍需要依赖误差较大、精度较低的传统差分方法离散空间算子，甚至在处理高维问题时需要进行较多的预处理工作。因此，以B 方法为基础的数值格式在未来仍有诸多亟待解决的问题，以及较大的提升空间。