双曲空间中子流形的积分公式 *
王琪,周志进
(贵阳学院 数学与信息科学学院,贵州 贵阳 550005)
1 引言
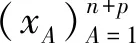
并令其装备双曲黎曼度量
则得到(n+p)维双曲空间Hn+p,其截面曲率K≡-1.
关于双曲空间Hn+1中等距浸入超曲面M,文献 [1] 曾给出一个经典的积分公式,即Minkowski公式,也即定理1.本文研究(n+p)维双曲空间Hn+p中n维等距浸入紧致无边子流形Mn.利用关于Codazzi张量场的一个已知定理,本文得到Mn的一个积分公式,即定理2.定理2推广了定理1的结果.
定理1[1]设h:M→Hn+1是定向的等距浸入紧致无边超曲面,记N为M的单位法向量场,而σk为M的k-平均曲率.则有积分公式

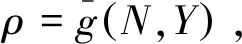
定理2设h:Mn→Hn+p是n维定向的等距浸入紧致无边子流形,记η为Mn的单位平均曲率法向量场,而σk为Mn沿方向η的k-平均曲率.则有积分公式
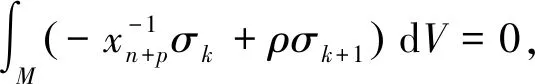
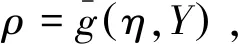
2 预备知识和引理
令(Mn,g)为一个n-维光滑黎曼流形,而S是Mn上一个(k,k)型张量场.如果S对其协变指标反对称,同时对其反变指标也反对称,则记S∈Γ(EndΛk(TM)).设S∈Γ(EndΛk(TM)),T∈Γ(EndΛj(TM)),定义S*T∈Γ(EndΛk+j(TM))为S与T的协变分量、S与T的反变分量分别作外乘积,而得到的(k+j,k+j)型张量场.由文献 [1-3] 知乘法*满足结合律和交换律.
定义1[1-3]( Codazzi张量场) 设S∈Γ(EndΛk(TMn)),并记∇为黎曼流形Mn的Levi-Civita联络.如果对任意的X1,X2,…,Xk+1∈Γ(TMn),0=∑(-1)j+1(∇XjS)(X1∧…∧Xj-1∧Xj+1∧…∧Xk+1)都成立,则称S为Mn上一个(k,k)型Codazzi张量场.
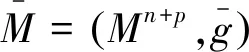

其中,I为End(Γ(THn+p))的恒同截面;f=-1/xn+p是广义位置向量场∂/∂xn+p相关联的光滑函数.
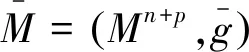
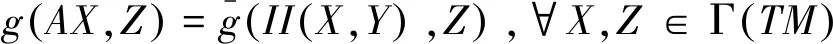
确定了Mn上一个(1,1)型Codazzi张量场A.其中II表示子流形Mn的第二基本形式.
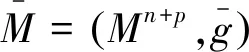
定义子流形Mn的平均曲率法向量场为
同时定义Mn的单位平均曲率法向量场为
Mn的平均曲率法向量场σ及其单位化η的定义与幺正局部标架场(eA)的选取无关.
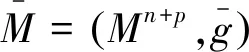
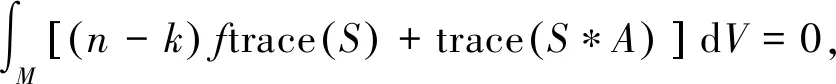
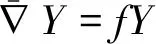
3 定理2的证明
证明令Tη为Mn沿其单位平均曲率法向量场η方向的形状算子,即
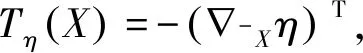

记λ1,λ2,…,λn为Mn沿η方向的主曲率,即λ1,λ2,…,λn为Mn沿η方向的第二基本形式的特征值.用δr表示λ1,λ2,…,λn的基本对称多项式,即
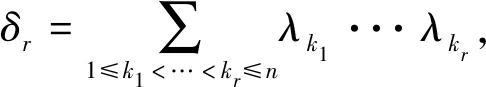
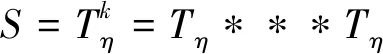
tarce(S)=k!δk.
(1)
令ρ表示Mn沿其单位平均曲率法向量场的支撑函数,即
其中Y=∂/∂xn+p是Hn+p的一个广义位置向量场 (见引理1).
由Tη以及 (1,1)张量场A的定义 (见定义3),计算得
A=ρTη.
用类似于 (1) 式的计算,得到
trace(S*A)=ρ(k+1)!δk+1.
(2)
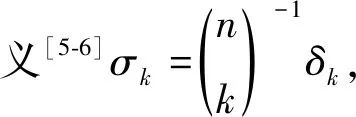
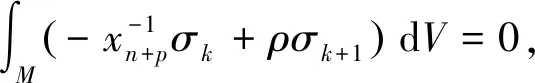
定理2得证.

