基于神经网络的大规模数据集离群点检测算法

高志宇， 宋学坤， 肖俊生， 闫培玲， 孙新娟

(1. 河南中医药大学 信息技术学院， 郑州 450046； 2.华北水利水电大学 物理与电子学院， 郑州 450045)

相对于大量常规数据来说，数据集中存在的离群点是一种异常孤立的数据模式[1].通常情况下，数据集中存在的离群点会被作为噪声而被消除，但部分离群点会存在一些重要的信息[2].离群点检测是结合可视化、统计学、智能计算、机器学习等多种技术对数据集中存在的离群点进行识别，便于后续的数据处理和分析的算法[3].由于离群点中可能存在有效信息，因此离群检测在气象预测、预防电信诈骗、市场分析、医疗保险和预防信用卡欺诈等领域中得到了广泛的应用，具有重要的现实意义和学术意义[4].

钱景辉等[5]提出了基于多示例学习的数据集离群点检测算法，该算法将真实对象在MIL框架中转变为多示例形式，结合权重调整方法和退化策略对综合离群点因子进行计算，实现对离群点的检测.经实践证明，相对于其他算法，该算法在数据检测全面性及高效性上有一定程度提高.顾煜炯等[6]设计了基于马氏距离的数据集离群点检测算法，该算法通过阶比重采样方法对大规模数据集中存在的原始数据进行预处理，并对数据进行量纲因子分析，结合马氏距离采用多元线性回归方法构建离群点检测模型，实现对大规模数据集离群点的检测.然而大规模数据集下量纲因子分析过程较为复杂，导致该算法转变数据形式所用的时间较长，存在检测效率低的问题.为同时实现离群点检测过程的高效性和检测结果的准确性，本研究利用神经网络设计了大规模数据集离群点检测算法.

1 大规模数据集降维处理

所设计的离群点检测算法首先采用核主成分分析方法对大规模数据集进行降维处理，去除大规模数据集中存在的冗余数据，进而缩短离群点检测过程所需的时间，提高检测效率.

(1)

式中，T为数据离散度.输入空间中存在的样本点，并通过非线性映射函数φ将其转变为特征空间中存在的样本点φ(x1)，φ(x2)，…，φ(xk)，…，φ(xM)[7].设C′为特征空间F中存在的协方差，可表示为

(2)

结合所得的特征空间协方差C′，可得到特征空间F中存在的特征值为

λ=φ(xk)C′v

(3)

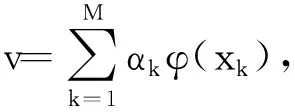
在此基础上，设置一个大小为M×M的矩阵G，在F空间上测试样本对应的投影为

(4)

如果在特征空间中，数据无法满足中心化条件，则要修正矩阵[8-9]，将G用G′进行描述，即

(5)

在此基础上，采用核主成分分析方法对大规模数据集进行降维处理，具体过程如下：

1) 用M×N维的矩阵A描述数据流中存在的M条数据记录.

2) 通过高斯径向基核函数对核矩阵H进行计算，计算表达式为

(6)

由式(6)可知，核矩阵与测试样本对应的投影存在直接关联，同时也受到输入空间中样本数据的影响.

3) 对核矩阵H进行局部修正.

4) 对H所对应的特征向量和特征值进行计算.

5) 按照降序对计算得到的特征值进行排序，并对特征量进行调整.

6) 通过Gram-Schmidt正交法对特征量进行单位化处理[10].

7) 对特征值对应的累积贡献率进行计算，从中提取t个主分量(β1，β2，…，βt).

8) 计算核矩阵H特征向量上存在的投影，即

(7)

根据式(7)中对特征量、核矩阵和特征值主分量的计算，获得降维处理后的大规模数据集.

2 离群点检测

一般来说，神经网络中包括输入层、输出层和隐含层，由目标分类标签个数和输入属性个数决定输出层神经元数目和输入神经元数目[11].

假设p、q分别代表神经元在隐含层和输出层的个数，则神经网络模型可描述为

(8)

(9)

式中：φj(xi)为第j个节点在神经网络中对应的输出；cj为高斯核函数对应的中心量；σj为第j个节点在高斯函数中的宽度；yi为第i个输出神经元在神经网络中对应的输出；Wij为第i个输出神经元与第j个隐节点之间存在的连接权重.

假设[xi，di]代表一组样本对，存在于训练过程中，其中，di表示输入量xi对应的目标量.通过样本确定神经网络中存在的未知参数，包括输出层、隐含层和隐节点中心之间的连接权值等[12-13].在构造神经网络的过程中，确定隐节点中心是较为重要的一步.而在所设计的基于神经网络的大规模数据集离群点检测算法中，通过减法聚类确定隐节点中心.

在减法聚类算法中可以用候选的隐节点中心代替数据对象，设Pi为中心对应的势，其计算表达式为

(10)

式中：r为邻域分簇中心对应的半径；xc为簇中心数据.减法聚类算法的具体过程如下：

1) 确定每个对象对应的势值Pi；

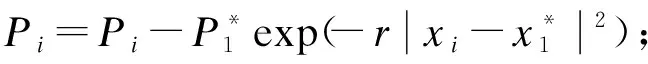
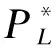
利用上述过程获得隐节点中心，通过反向传播算法在神经网络中更新连接权重，在更新权重的基础上获得输出与输入在神经网络中存在的映射关系[14-15].

(11)

设E为神经网络的误差能量，其计算表达式为

(12)

在训练过程中引入调整项，对误差函数进行调整[16]，调整表达式为

(13)

在误差函数的基础上构建大规模数据集离群点检测模型，通过检测模型实现大规模数据集离群点的检测，检测表达式为

(14)

综上所述，实现了对基于神经网络的大规模数据集离群点检测算法的设计.算法具体实现流程如图1所示.

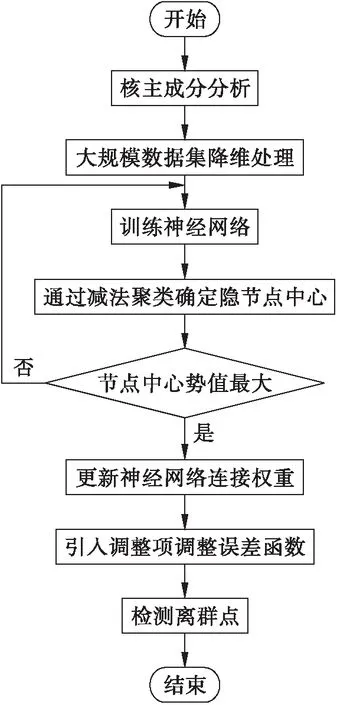
图1 大规模数据集离群点检测算法运行流程Fig.1 Operational process of outlier detection algorithm for large-scale data sets

3 实验结果与分析

为证明基于神经网络大规模数据集离群点检测算法的整体有效性，设计实验加以验证.实验环境及参数设置情况如表1所示，其中，Communication Database数据库由若干个可更新的系统表构成.

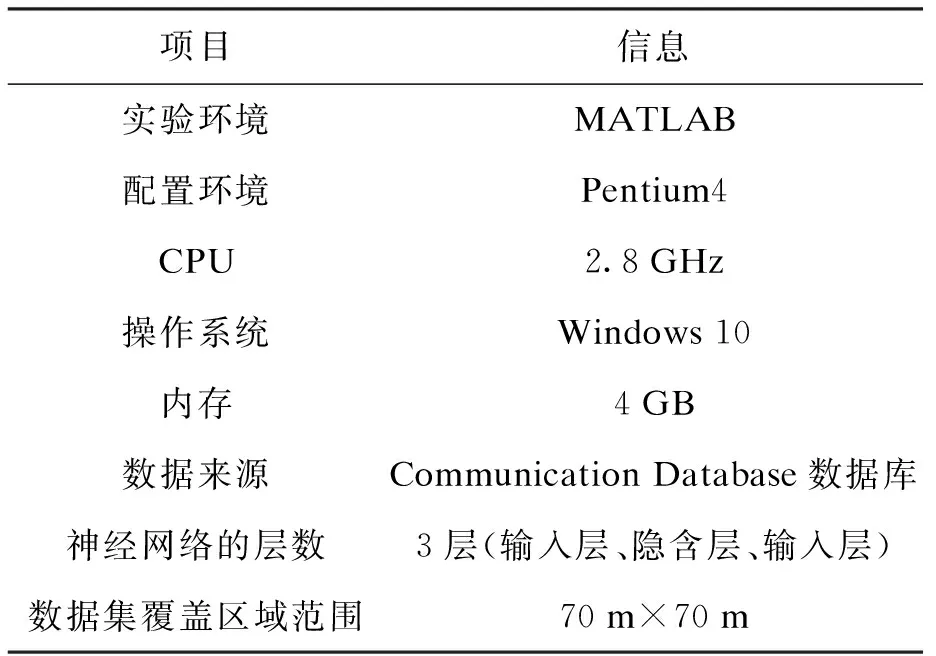
表1 实验环境及参数设置Tab.1 Experimental environment and parameter settings

本文从检测耗时和检测准确率两个角度，在相同的实验环境和参数设置情况下，对基于神经网络的大规模数据集离群点检测算法、基于多示例学习的数据集离群点检测算法和基于马氏距离的数据集离群点检测算法进行性能测试.

3.1 检测准确率

首先利用高斯函数结合降维处理，生成大规模数据集，数据集中共含有1 000个二维数据，在其中加入10个具有较大偏差的离群点，得到一个包含有1 010个二维数据的仿真数据集.然后利用基于神经网络的检测算法对其中的离群点进行检测，检测结果如图2所示.

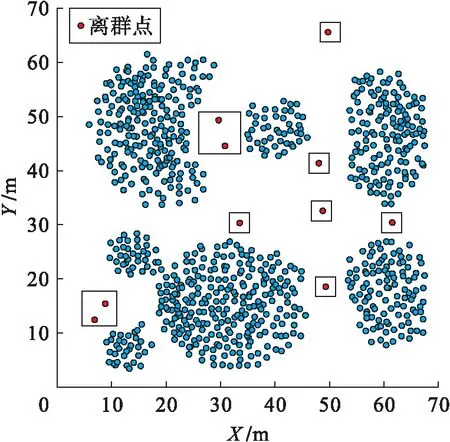
图2 离群点检测结果Fig.2 Outlier detection results

由图2可知，利用基于神经网络的检测算法能够有效检测出样本集中所含的10个离群点，由此，初步证明了该算法的有效性.在此基础上，利用高斯函数结合降维处理，随机生成一个新的大规模数据集，新的数据集中共含有10 000个二维数据，然后在其中加入了100个具有较大偏差的离群点，得到一个包含有10 100个二维数据的样本集.利用此样本集测试不同检测算法的检测准确率，对比结果如图3所示.

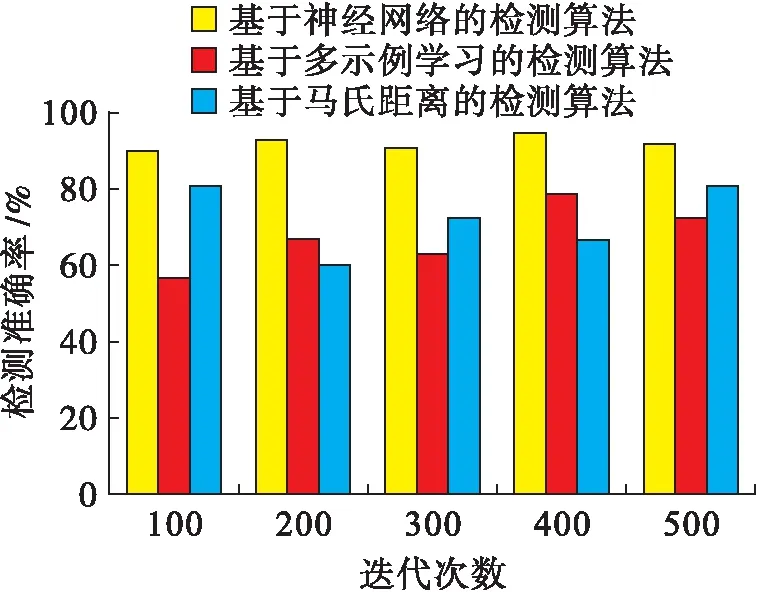
图3 不同算法的检测准确率Fig.3 Detection accuracy of different algorithms

测试第500次迭代时不同算法的检测结果，观察其未能有效识别出的离散点情况，并以散点图的形式体现，结果如图4所示.

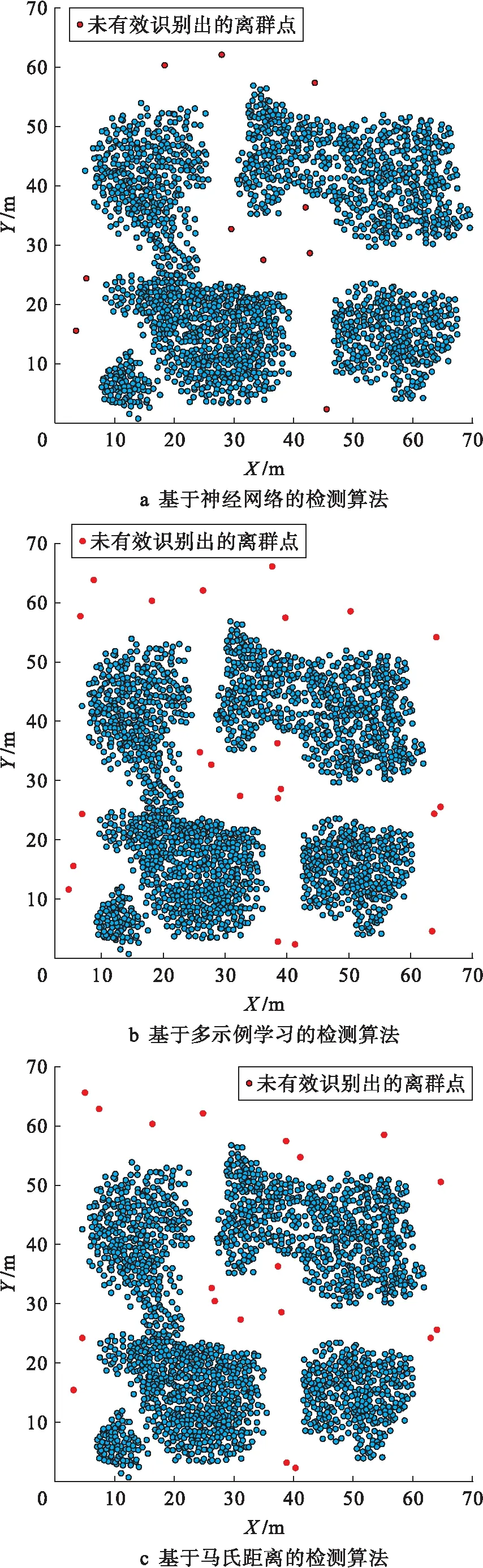
图4 第500次迭代时不同方法检测结果Fig.4 Test results of different methods at 500th iteration

综合分析图3、4可知，在多次迭代中，基于神经网络的检测算法可有效地对大规模数据集中存在的离群点进行检测，且检测准确率始终保持在90%以上，明显高于2种对比检测算法.原因在于基于神经网络的检测算法在误差函数的基础上构建离群点检测模型，通过调整误差能量提高最终的检测准确率.

3.2 检测耗时

检测耗时可以体现不同算法对离群点检测的效率.利用操作系统后台自动统计不同算法的检测过程耗时，测试结果如图5所示.

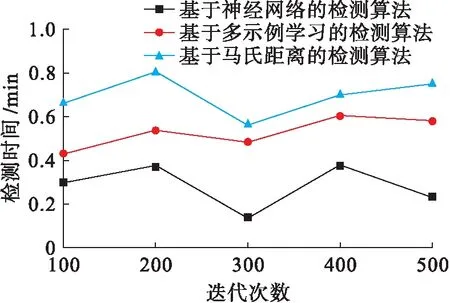
图5 不同算法的检测时间Fig.5 Detection time of different algorithms

根据图5可知，在多次迭代中，基于神经网络的检测算法对离群点的检测时间始终低于0.4 min；基于多示例学习的检测算法在第400次迭代过程中所用的检测时间高达0.6 min；基于马氏距离的检测算法在第200次迭代中所用的检测时间高达0.8 min.对比这3种检测算法的测试结果可知，基于神经网络的检测算法检测离群点所用的时间最短，证明该算法检测效率最高.采用核主成分分析方法对大规模数据集进行了降维处理，去除了大规模数据集中存在的冗余数据和无用数据，因此有效缩短了检测用时.

4 结 论

针对当前离群点检测算法存在的检测效率及检测准确率低的问题，本文利用神经网络设计了一种大规模数据集离群点检测算法.研究发现：采用核主成分分析方法对数据进行降维处理，通过去除冗余数据和无用数据的方式可以有效缩短检测用时，且在建立误差函数的基础上通过调整误差能量提高最终的检测准确率.本文也通过实验证明了该算法能够在较短的时间内，准确地对大规模数据集中离群点进行检测.