基于GA改进LSTM-BP神经网络的智慧楼宇用能行为预测方法
江世雄, 黄鸿标, 陈苏芳, 肖荣洋
(1. 武汉大学 动力与机械学院, 武汉 430072; 2. 国网福建省电力有限公司 龙岩供电公司, 福建 龙岩 364000)
随着人口的持续增长与经济的飞速发展,全球能源消耗和环境问题已逐渐成为研究热点[1].根据相关数据显示,全球约有39%的能源消耗及38%的温室气体排放来自于建筑能耗[2-3],因此有必要对建筑能耗进行合理的预测与控制,以提供更加精准的能源供应,从而缓解能源紧缺态势并减少温室气体的排放[4].
国内外对建筑能耗已有诸多研究,如周璇等[5]针对建筑内照明及插座能耗具有随机性且难以预测的特征,利用长短时记忆网络(LSTM)模型提出了基于深度学习的多步预测建模方法,有效提高了预测精度,但其对于楼宇能耗的全方位预测效果仍有待深入研究;李红莲等[6]利用历史气象和能耗数据,采用Morphing法对国内典型城市办公建筑的全年能耗进行模拟,预估了气候变化下建筑能耗的变化趋势,为更加精准的能源供应提供了依据;Damrongsak等[7]研究了商场能耗数据,并提出一种多元线性回归方法深入挖掘了能源消耗与其他环境参数的关系,进而有效预测了建筑物电能消耗;而Kannari等[8]提出了一种结合物理建模与机器学习的新方法,通过人工神经网络完成对数据集参数的训练和学习,其兼顾了预测模型鲁棒性、准确性及推理速度.
但上述方法对能耗的预测大多仅针对于电能,故在实际建筑物能耗的预测中存在一定局限性[9],因此,本文基于遗传算法(GA)改进LSTM-BP神经网络,提出了一种智能建筑用能行为的预测方法.
1 基于聚类算法的用户用能行为分析
在智慧楼宇用能行为预测之前,需要明确用能类型,因此所提方法基于K-means聚类算法来划分楼宇的用能类型,从而提高后续预测的准确性.
1.1 K-means算法
算法将一组N个未标记的数据量聚类划分为K个类型,且每个簇的质心可计算为同一簇中所有数据点的平均值,聚类过程如下:
1) 随机或根据一些先验知识初始化k个数据点R=[R1,R2,…,Rk].
2) 计算每个数据点x与质心之间的距离,并将每个数据点指定给最近的质心.数学公式表述为
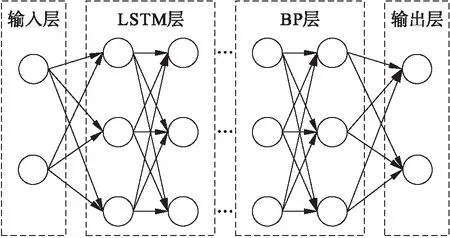
xi∈Rwifd(xi,Rw) (1) 式中,d(xi,Rj)表示数据点xi和质心Rj之间的距离,且所提方法采用欧几里德距离. 3) 重新计算每个簇的质心,直至收敛,质心计算表达式为 (2) 式中,Nk为数据点质心的数量. 智能楼宇使用的能源主要有电能、天然气、冷能及热能等[10],本文通过各自的测量装置获取数据,并利用K-means聚类算法进行分析处理,从而得到楼宇用能行为特征.其中,以某工业住宅小区混合楼宇为目标,选取常用的电能、热能与冷能作为能耗研究对象进行分析,则该智慧楼宇的电能消耗曲线如图1所示. 图1 电能消耗曲线Fig.1 Electric energy consumption curves 由图1可以看出,用户用电行为习惯可分为4种类型,分别表示为EA、EB、EC和ED.EA曲线平行于水平轴,则此类用户整体功率较低,无明显波动且功耗小,故可推测其处于空载状态,仅有少量线损;EB用户曲线波动明显,用电高峰主要出现在早晚时段,且昼夜曲线波动较小,所以其大概率为上班族;EC曲线全天呈现多个功率峰值,且峰值在早期、中期和晚期均有出现,则推测用户为老年家庭;而ED的能量消耗曲线在一天中呈现多个峰值,但白天为一个小峰值,夜间则是一个远高于其他曲线的大峰值,因此该用户可能是有几代人的混合家庭. 同样,以该小区冬季某一天热能消耗作为研究对象,获得的热能变化曲线如图2所示. 图2 热能消耗曲线Fig.2 Thermal energy consumption curves 从图2可以看出,热能消耗行为可分为3类:GA曲线的高峰仅出现在早晚,因此用户大概率是上班族;GB曲线全天均呈现多个能耗峰值,说明楼宇内全天候有人,故此类用户应是几代人的混合家庭;GC曲线几乎仅在晚间有高耗能,所以用户有可能是学生类型的人群. 对于楼宇冷能消耗,则主要选取夏季某典型高温天气作为研究对象,能耗曲线如图3所示. 图3 冷能消耗曲线Fig.3 Cold energy consumption curves 由图3可知,对于冷能的消耗,不同用户具有不同的表现.其中CA表现为非工作时间较为明显,而上班时间几乎无冷能消耗,大概率为上班族;CB和CC则与之相反,大部分冷能负荷为白天工作时间,大概率为工业或企业用户,且在部分时间呈现用能高峰. LSTM网络主要通过输入门、遗忘门和输出门来实现信息的保护与控制.其中遗忘门表示网络从单元中丢弃的信息,即通过读取前一时刻的输出结果ht-1和外部输入xt,以输出“0”或“1”,“1”表示完全保留,而“0”表示完全接受.LSTM的遗忘门计算表达式为 f=δ(ωf[ht-1,xt]+bf) (3) 式中:δ为激活函数;ω、b分别为网络的权重和偏置量. (4) 最终输出门的计算表达式为 (5) LSTM神经网络的结构对其预测性能具有显著影响,为此引入反向传播神经网络(BP)用于确定各种权重值与偏差,以提高模型的预测准确性.所构成的LSTM-BP神经网络的整体结构如图4所示. 图4 LSTM-BP神经网络的整体结构Fig.4 Overall structure of LSTM-BP neural network 在LSTM-BP神经网络中,原始数据输入LSTM网络的输入层,考虑到数据过载问题,将遗忘门设为一层且其神经元数量不超过30个.然后将LSTM网络的输出层数据作为BP神经网络的输入,经过分析处理后得到最终的预测结果.其中将BP神经网络的隐藏层设为3层,而每层神经元的数量则需根据实际研究对象进行选取. 为了使LSTM-BP神经网络架构具有多维空间,故采用GA优化确定LSTM-BP超参数的最佳值,其包括LSTM及BP网络层次数量[11-12]、每层中神经元数量以及相应的丢弃率与学习率. GA算法是一种基于自然选择理论以及遗传机制的强大进化算法.其将待优化参数组成编码串,并根据一定的适应度函数和一系列遗传操作对每个个体进行种群筛选,从而保留具有高适应度值的个体,再形成新的群体.新群体中个体的适应值不断提高,直至满足迭代终止条件,具有最高适应值的个体即为优化参数的最优解[13].由于GA算法独特的相似性与生物进化的工作原理,使其能在复杂空间中进行全局优化搜索,且具有较强的鲁棒性[14]. GA算法优化LSTM-BP神经网络的具体步骤如下: 1) 参数初始化:设置种群规模、交叉概率、变异概率、最大迭代次数及误差极值等主要参数. 2) 根据个体适应度值的大小进行排序,并计算每个个体的评价函数,其中将预测模型的平均绝对误差(MAE)作为适应度值[15],然后对其排序并将计算出的平均适应度值作为阈值,再选择适应度大于平均适应度的个体组成新的种群. 3) 确定是否达到所需的种群规模,若达到,进行交叉、变异遗传操作等;否则重复步骤2). 4) 根据寻优得到的最优个体作为LSTM-BP神经网络的权值和阈值. 5) 使用LSTM-BP神经网络传播正信息,计算全局误差并判断是否达到迭代终止条件.若满足条件,结束模型学习并输出预测结果;否则进行LSTM-BP网络的反向传播,修改权重并返回至步骤4),重复模型学习. 利用GA优化的LSTM-BP神经网络模型来预测智慧楼宇的用能行为.将智慧楼宇的电能、天然气等能源使用量以及当地天气状态的信息输入预测模型,从而实现对用户用能行为的预估.所提智慧楼宇用能行为预测流程如图5所示,主要流程如下: 图5 基于改进LSTM-BP模型的用能行为预测流程Fig.5 Prediction process for energy consumption behavior based on improved LSTM-BP model 1) 采集用能数据并对其进行聚类预处理,得到楼宇明确的用能类型.同时,将数据集划分为训练集和测试集. 2) 训练LSTM模型并初始化预测模型参数,然后将训练集输入模型,利用GA算法进行反复迭代优化,得到MAE最小化的模型参数. 3) 训练BP模型,将LSTM模型输出值作为BP网络的输入进行训练.同样,利用GA算法优化BP网络模型的参数,当达到预设目标,则能够获得最佳的LSTM-BP网络预测模型. 4) 将测试集数据输入训练好的LSTM-BP模型中,对模型输出的数据进行反归一化处理,并将预测结果与实际样本加以对比,从而得到高精度的用能行为预测结果. 基于TensorFlow深度学习框架对所提方法进行实验分析.其中,数据集选取东部地区某智慧住宅2020年3月12日至2020年5月20日的用户耗能相关数据.信息采集频率为30 min,共1.43×107条用户信息用于智慧楼宇用能行为的分析预测. 由于GA算法中选择、交叉和变异概率的选值对所提方法的预测性能存在较大影响,故将种群规模与最大迭代次数分别设为20及50.在不同选择、交叉和变异概率下所提方法的MAE变化如图6所示.经过GA算法改进后的模型中LSTM隐藏层为2层,BP神经网络隐藏层为3层,加上输出与输入层,整体模型共有7层.其中LSTM每层28个神经元,BP神经网络每层神经元个数为31个. 图6 不同选择、交叉和变异概率下的模型MAE变化曲线Fig.6 MAE variation curves under different selection, crossover and mutation probabilities 由图6可以看出,优化迭代开始时MAE波动较大,迭代次数超过30后,预测模型趋于收敛.交叉操作的概率用于判定两个个体是否进行交叉,变异操作的概率表示允许少数个体存在变异情况,以避免陷入局部最优,其取值应综合考虑算法性能.当选择概率取值较小时,算法收敛较慢甚至不收敛.当选择、交叉及变异概率分别为0.8、0.2和0.2时,MAE将达到最小,且仅为1.85 J.因此在本方法中将GA算法的3种概率值分别设为0.8、0.2和0.2,以实现最佳的预测性能. 针对智慧楼宇用户常用的电能、热能及冷能耗量进行预测分析,采用12 h与48 h的预测结果如图7所示. 图7 所提方法不同时间范围的预测结果Fig.7 Prediction results obtained by as-proposed method within different time ranges 由图7可以看出,12 h的预测值与实际值基本一致,而48 h的预测值与实际值则仍存在一定偏差.原因是时间范围越广,可变因素越多,对模型的预测性能要求也就越高.从电能耗量曲线中可明显看出,48 h的预测值存在明显的波动,这可能是所提模型出现了过度收敛,且电能受环境、社会因素影响较大而导致的结果.但总体而言,本文方法的预测结果与真实值基本接近,满足设计目标. 为了论证所提方法的预测性能,将其与文献[5]、文献[7]及文献[8]的预测结果进行对比,如图8所示. 图8 不同方法的MAE对比结果Fig.8 MAE comparison results among different methods 由图8可以看出,相比于其他对比方法,所提方法能实现最快收敛且MAE值最小.由于所提方法在K-means聚类获得用户行为类型的基础上,通过利用LSTM-BP神经网络学习分析得到预测结果,所以能最大程度地保证预测准确性.然而文献[5]使用LSTM网络以及文献[7]仅采用多元线性回归方法来进行预测,单一模型的处理性能不佳,故二者预测误差均较大;而文献[8]在物理建模的基础上利用人工神经网络实现能耗预测,预测性能较单一模型有所提升,但缺乏多能源类型的考虑. 随着“碳达峰”、“碳中和”战略目标的实施,对于高耗能的智慧楼宇进行节能减排成为了必然趋势.本文提出了一种用能行为预测方法,为能源调控提供参考.通过引入K-means聚类算法对用户的用能行为类型进行划分后,将用能数据输入GA改进的LSTM-BP模型进行预测分析,以估计智慧楼宇的用能行为.基于TensorFlow框架的实验结果表明,当选择、交叉及变异概率分别为0.8、0.2与0.2时,所提方法的性能最佳.算法MAE值约为1.79 J,因此能够稳定、高精度地预测不同时间的智慧楼宇用能行为.1.2 智慧楼宇用能行为特征



2 智慧楼宇用能行为预测模型
2.1 LSTM-BP神经网络

2.2 基于GA改进的LSTM-BP网络模型
2.3 基于改进LSTM-BP的用能行为预测模型

3 实验结果与分析
3.1 参数分析

3.2 用能行为分析

3.3 预测性能分析

4 结 论

