面向神经形态感知和计算的柔性忆阻器基脉冲神经元*

朱佳雪 张续猛 王睿 刘琦†

1) (中国科学院微电子研究所,微电子器件与集成技术重点实验室,北京 100029)

2) (复旦大学,复旦大学芯片与系统前沿技术研究院,上海 200433)

3) (中国科学院大学,北京 100049)

4) (上海期智研究院,上海 200232)

受人脑工作模式的启发,脉冲神经元作为人工感知系统和神经形态计算体系的基本计算单元发挥着重要作用.然而,基于传统互补金属氧化物半导体技术的神经元电路结构复杂,功耗高,且缺乏柔韧性,不利于大规模集成和与人体兼容的柔性感知系统的应用.本文制备的柔性忆阻器展示出了稳定的阈值转变特性和优异的机械弯折特性,其弯折半径可达1.5 mm,弯折次数可达104 次.基于此器件构建的神经元电路实现了神经元的关键积分放电特性,且其频率-输入电压关系具有整流线性单元相似性,可实现基于转换法的脉冲神经网络中神经元的非线性处理功能.此外,基于电子传输机制和构建的核壳模型,对柔性忆阻器的工作机制进行分析,提出了电场和热激发主导的阈值转变机制;进一步对忆阻器和神经元的电学特性进行电路仿真模拟,验证了柔性忆阻器和神经元电路工作机制的合理性.本文对柔性神经元的研究可为神经形态感知和计算系统的构建提供硬件基础和理论指导.

1 引言

近年来,人工智能、物联网、智能穿戴等领域的发展,对海量数据的快速高效处理提出了更高的要求.基于冯·诺依曼架构的传统计算系统,由于存储器和处理器的物理分离导致了“存储器”瓶颈[1],难以实现智能系统的高效数理处理.受人脑工作模式的启发,以脉冲神经元为计算单元的神经形态计算架构体系应运而生,它具有并行信息处理、低功耗、高容错性等优点[2],使其在处理高维和非结构化数据方面显示出巨大优势,为智能系统的设计提供了备选方案.然而,当前神经形态芯片[3-7]所使用的神经元大多基于互补金属氧化物半导体(complementary metal oxide semiconductor,CMOS)技术,由于晶体管缺乏内在动力学特性和生物单元相似性,其所构建的神经元电路不但结构复杂,集成度低,而且学习能力欠缺[8].因此,亟需寻找结构简单、集成度高、内在动力学丰富的神经形态器件构建紧凑的神经元电路,从而实现更高效的神经形态系统.

在众多的神经形态器件(如阻变存储器[9]、相变存储器[10]、磁自旋存储器[11]、铁电存储器[12]、突触离子晶体管[13])中,阻变存储器(后续称为忆阻器)因其结构简单,转变速度快,功耗低,动力学特性丰富等优点[9,14],在存内计算[15]、突触功能模拟[16]和人工感知系统[8,17,18]等领域备受研究人员关注.此外,忆阻器所展现出的阈值转变特性还被用于神经元电路的设计中,并在人工感知系统和神经形态计算等领域获得应用[19-22].例如,Zhang 等[23]利用NbOx基忆阻器设计了漏电-积分-发射(leaky integrate-and-fire,LIF)神经元,并实现了人工传入神经的模拟.Lashkare 等[24]基于PrMnO3忆阻器设计的神经元具备整流线性单元(rectified linear unit,ReLU)功能,可用于脉冲神经网络的激活函数模拟.然而,目前基于忆阻器所设计的神经元均缺乏柔韧性,不利于智能皮肤、人工义肢、健康监测等柔性感知方面的应用.此外,忆阻器基脉冲神经元在神经形态计算的非线性变换功能领域也有着重要应用[20,23-28].因此,设计和开发一种基于柔性忆阻器的脉冲神经元用于智能感知和计算系统,对忆阻器基神经元的功能挖掘和应用推广意义重大.

本研究组制备了一种柔性的阈值转变型忆阻器,该器件表现出了优异的机械弯折特性,其弯折半径可达1.5 mm,弯折次数可达104次.基于此器件设计的柔性神经元电路具备阈值发放、“全”或“无”、不应期和输入强度依赖的频率调制特性,可将模拟的输入信号转换成脉冲频率信号,用于人工感知系统的应用.此外,该神经元表现出的频率-电压强度关系具有ReLU 激活函数相似性,可用作神经形态计算的非线性变换单元.针对柔性神经元表现出的频率和阈值电压随输入信号强度的变化关系,对柔性忆阻器的电子传输机制和阈值转变机制进行了分析,并通过电路仿真技术进行了验证,得到了电场和焦耳热主导的阈值转变机制,揭示了柔性衬底的热积累效应对器件阈值电压和神经元放电频率的影响.最后,基于构建的柔性神经元电路搭建了两层神经网络(784 × 100 × 10)系统来识别数字手写体,得到了约95.6%准确率,与理想情况相当.本研究为柔性神经元的设计和工作机制分析提供了参考,阐述了其在柔性感知和神经形态计算中的应用潜力.

2 实 验

柔性NbOx忆阻器的制备流程如图1 所示.首先,通过旋涂法在清洗后的Si 片上涂布聚酰亚胺(polyimide,PI)溶胶,之后将样品置于鼓风干燥箱中加热干燥,直至形成表面光滑且厚度均一的PI 薄膜(厚度约为30 µm).为保证后续薄膜的沉积质量,在PI 薄膜表面上通过磁控溅射法生长100 nm 厚的SiO2薄膜来获得更加光滑和致密的表面.随后,利用紫外光刻技术和剥离法对后续薄膜进行图案化,结合磁控溅射法和电子束蒸发法依次生长5/35 nm 的Ti/Pt 底电极、50 nm 的NbOx阻变层和5/35 nm 的Ti/Pt 顶电极.其中,器件的有效面积为5 µm×5 µm.最后将PI 薄膜从Si 衬底上剥离,于是,柔性PI/SiO2/Ti/Pt/NbOx/Ti/Pt结构的忆阻器制备完成.

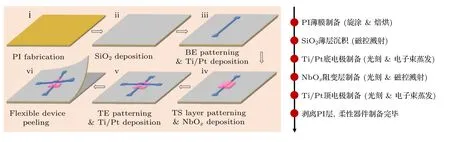
图1 柔性PI/SiO2/Ti/Pt/NbOx/Ti/Pt 结构忆阻器制备流程图Fig.1.Flow chart of the flexible PI/SiO2/Ti/Pt/NbOx/Ti/Pt structured memristor device.

3 实验结果与讨论

3.1 柔性忆阻器基本电学特性

柔性忆阻器的结构如图2(a)所示,其中PI 薄膜为柔性衬底,在所有的电学测试中底电极Pt 接地,而在顶电极Ti/Pt 上施加电压.器件经电激活过程后呈现出如图2(b)所示的阈值转变行为,即在正向的扫描电压下,流过器件的电流随着电压的增加而增大,直至电压达到阈值电压(the threshold voltage,VTH),电流突然增加至限制电流(compliance current,ICC) 500 µA,器件从高电阻状态(the high resistance state,ROFF)转变为低电阻状态(the low resistance state,RON);随着反向扫描电压降低至保持电压(the hold voltage,VH),电流突然降低,器件从低电阻状态转变为高电阻状态转变,完成器件的关闭.从图2(b)中可以看出,在50 次电学操作下,器件的稳定性良好,从中提取VTH和VH,二者的累积分布函数如图2(c)所示,分布均一且离散性小,说明器件具有稳定的阈值转变行为.此外,对不同器件间VTH和VH的差异性进行了表征,如图2(d)所示,在测试的10 个器件中,VTH和VH虽有一定的离散性,但二者的分布范围无重叠,且器件的阈值转变窗口(VTH—VH)均大于0.2 V,可防止电压误读,具有较强的抗干扰能力,可用于后续神经元电路的构建.

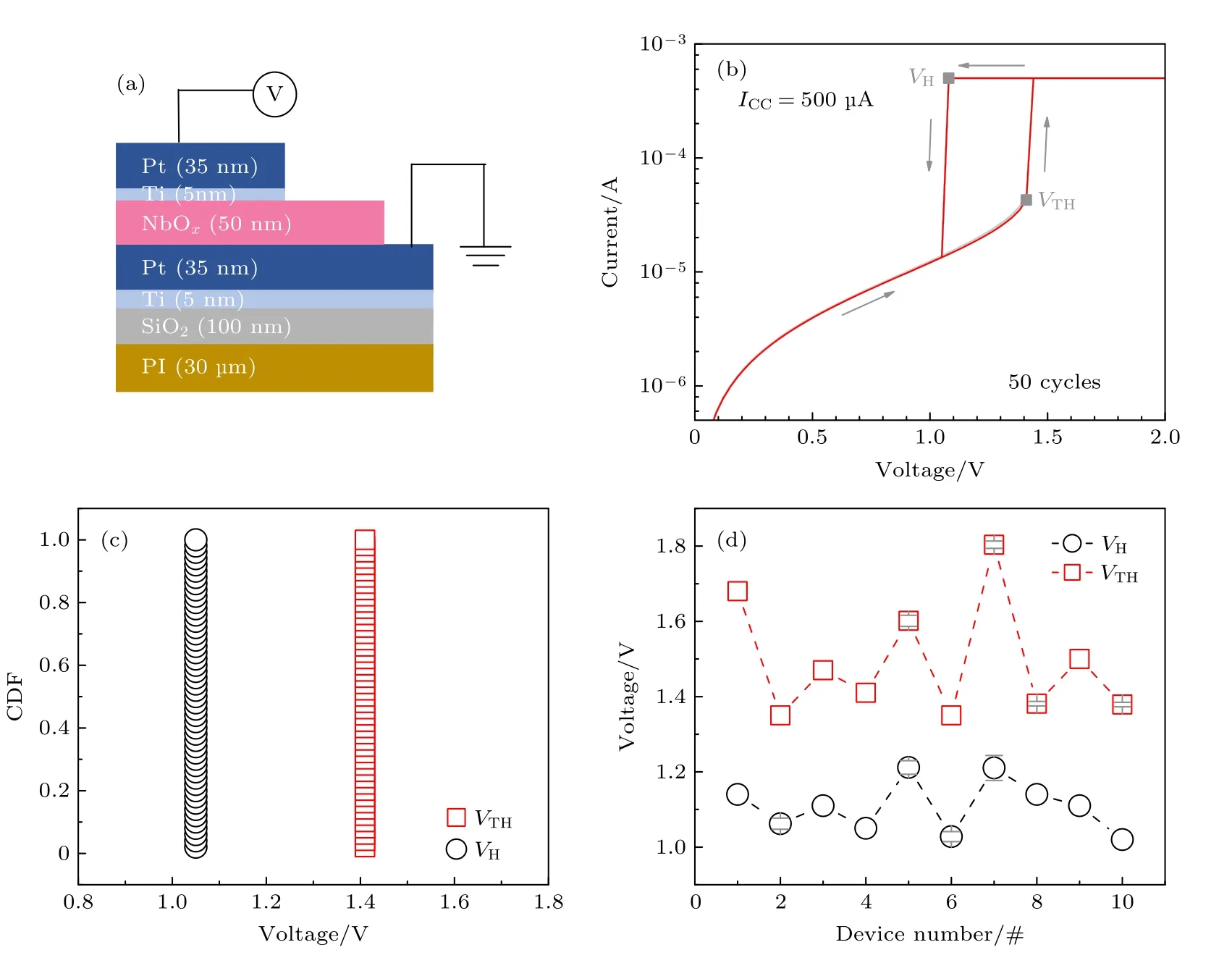
图2 柔性忆阻器基本电学特性 (a) 柔性PI/SiO2/Ti/Pt/NbOx/Ti/Pt 忆阻器结构示意图;(b) 忆阻器基本I-V 曲线;(c) 50 次电学循环下阈值电压和保持电压的累积分布函数;(d) 器件差异性表征Fig.2.Basic electrical characteristics of flexible memristor:(a) Structure diagram of PI/SiO2/Ti/Pt/ NbOx/Ti/Pt memristor device;(b) basic current-voltage (I-V ) curve of memristor;(c) cumulative distribution function of threshold voltage and hold voltage under 50 cycles;(d) variation of device to device.

3.2 柔性忆阻器弯折能力表征

为表征柔性忆阻器的机械弯折能力,在不同弯折半径和弯折次数下对器件的性能进行了测试.如图3(a)所示,将柔性忆阻器缠绕在不同半径的玻璃棒表面,并将其固定在载玻片上进行电学测试,获得了如图3(b)所示的I-V曲线.从图3(b)中可以看出,器件在不同弯折半径(3.5—1.5 mm)下均表现出阈值转变现象.在每个测试条件下,提取50 次电循环中的VTH和VH并作误差统计分布,如图3(c)所示.从图中可以看出,VTH和VH在不同弯折半径下的标准偏差(σ/µ)分别为2.3%和1.3%,虽有一定的波动性,但二者并未有重叠,说明器件在弯折条件下具有稳定性,表明了器件具有良好的可弯折能力.

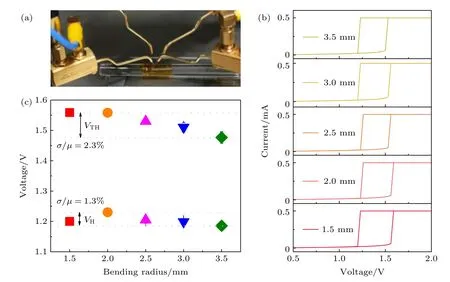
图3 不同弯折半径下器件的电学特性 (a) 不同弯折半径的测试图片;(b) 不同弯折半径下的I-V 曲线;(c) 不同弯折半径下50 次电学循环的阈值电压和保持电压统计Fig.3.Electrical characteristics of devices at different bending radii:(a) Test image of different bending radii;(b) I-V curves at different bending radii;(c) VTH and VH statistics for 50 cycles at different bending radii.

其次,对器件在弯折条件下的抗疲劳特性进行了表征.如图4(a)所示,将柔性器件粘贴在丝杆滑台组件的滑台上,滑台由步进电机带动做往复运动,滑台距离固定端的最大距离可使器件展平,而最小距离使得器件的弯折半径为2.5 mm.基于此装置,对不同弯折次数下的器件性能进行了测试,如图4(b)所示,器件在不同弯折次数 (1—104) 下均展现了稳定的阈值转变特性,且在往复弯折104次后,器件的VTH和VH基本保持不变(图4(c)),表明制备的柔性忆阻器具有良好的弯折耐受性.

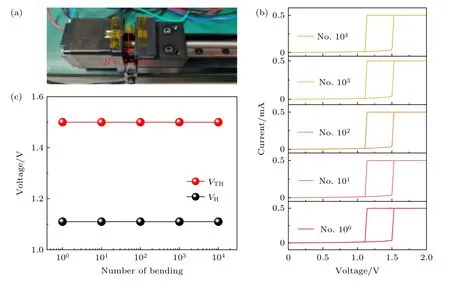
图4 不同弯折次数下器件的电学特性 (a) 不同弯折次数的测试图片;(b) 不同弯折次数下的I-V 曲线;(c) 不同弯折次数下50 次电学循环的阈值电压和保持电压统计Fig.4.Electrical characteristics of devices after different cycles of bending:(a) Test image of different cycles of bending;(b) I-V curves after different cycles of bending;(c) VTH and VH statistics of 50 cycles after different cycles of bending.

3.3 柔性忆阻器基脉冲神经元

基于柔性忆阻器及其阈值转变特性,构建了如图5(a)所示的忆阻器基脉冲神经元电路(memristive spiking neuron,MSN).该电路由一个负载电阻(the load resistance,RL),一个柔性忆阻器,一个串联电阻(the series resistance,RS)和一个电容器(capacitor,C)组成.其中电容器可为忆阻器的内部电容、电路的寄生电容或外部接入的电容.值得注意的是,这里为了定量表示电容值,以便后续仿真,采用了外接的电容器,而在实际应用中,可根据具体的需求,去掉外接的电容器,利用忆阻器本身的寄生电容来维持神经元的工作,从而增加集成度.在本节测试中,RL,RS和C的值分别为30 kΩ,100 Ω 和1 nF,而忆阻器的ROFF和RON分别约为200 kΩ 和1 kΩ.当对电路进行供电时,由于忆阻器处于高阻态,此时“1-2-4-1”环路的RC时间常数τ1=RL×C小于“2-3-4-2”环路的RC时间常数=(ROFF+RS)×C,所以先对电容器进行充电,直至节点“2”处的电压,即电容电位达到忆阻器的阈值电压,忆阻器由ROFF转变为RON;此时环路“2-3-4-2”处的RC时间常数τ2=(RON+RS)×C小于τ1,电容器进行放电,直至节点“2”处的电压达到忆阻器的保持电压,忆阻器由RON转变为ROFF,电容器进行新一轮的充放电.如图5(b)所示,当电路的输入电压(the input voltage,VIN)为4 V 的固定电压时,稳定工作状态下节点“2”处的电位(记为神经元的输出电压)在VTH和VH之间进行振荡,而从节点“3”处采集到的电流信号则为脉冲形式,为神经元的脉冲输出.当输入信号为图5(c)所示幅值递增的脉冲信号时,只有电容电位达到VTH(约2.0 V)时,才会有脉冲信号输出,表现出阈值发放特性;而当电容电位低于VTH时,则无脉冲输出,体现了神经元的“全”或“无”特性.此外,神经元在放电期间,表现出不应期特性,如图5(d)所示,当神经元开始发放脉冲时,随后施加在输入端的脉冲并不能引起神经元的再次放电,直至神经元完成一次放电行为,此段时间间隔称作不应期,与生物中的不应期概念相对应.这些结果表明本文所构建的柔性忆阻器基脉冲神经元电路具备了生物神经元的多种关键放电特征,能够把输入的模拟信号转换为脉冲信号,可用作人工感知系统中的感觉神经元,而器件本身所具有的柔性使其特别适用于人工义肢、神经界面和类人机器人等柔性感知应用.

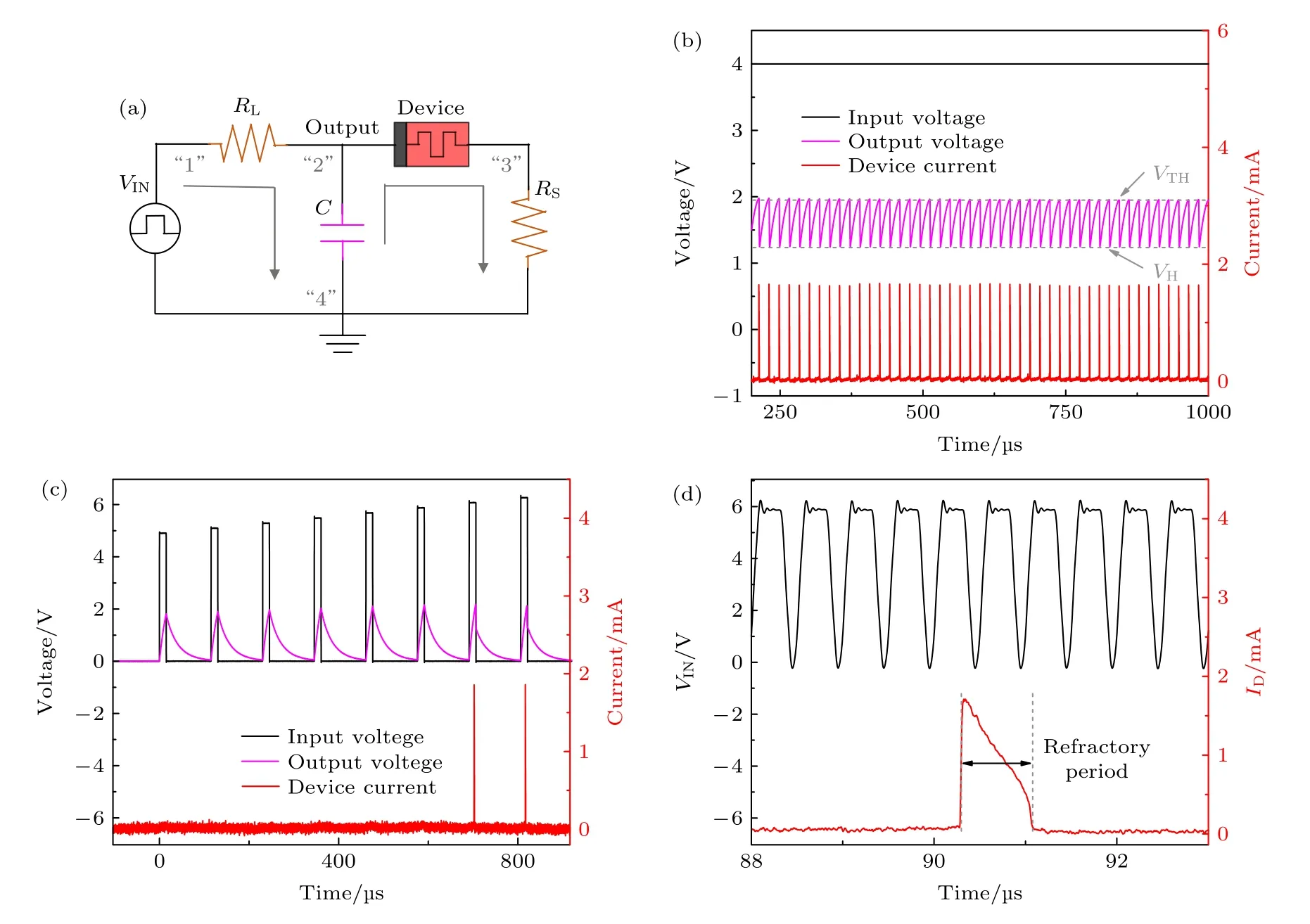
图5 柔性忆阻器脉冲神经元的关键特征 (a) 基于柔性忆阻器的脉冲神经元电路原理图;(b) 忆阻器脉冲神经元的振荡特性和脉冲输出特性;(c) 忆阻器脉冲神经元的全或无特性;(d) 忆阻器脉冲神经元的不应期特性Fig.5.Key features of flexible memristive spiking neuron:(a) Schematic diagram of spiking neuron circuit based on flexible memristor;(b) oscillation and output characteristics of memristive spiking neuron;(c) all or nothing characteristic of memristive spiking neuron;(d) refractory period characteristic of memristive spiking neuron.

另一方面,基于柔性忆阻器的神经元电路表现出线性的输出频率-输入电压依赖关系,使其可用于人工神经网络中ReLU 激活函数的模拟.如图6(a)所示,当神经元有正向输入时,ReLU 神经元的输出线性依赖于输入(图中斜线部分),而对于负向输入,ReLU 神经元则无输出,此特性可通过柔性忆阻器神经元进行模拟.图6(b)展示了神经元电路在阶梯型的脉冲电压输入下神经元的振荡输出结果.对输入的电压脉冲的频率和幅值进行统计,结果见图6(c),(d).从图6(c)中可以看出,当输入电压大于等于4 V 时,神经元的输出频率随着输入电压的增大而线性增加;而当输入电压小于4 V 时,神经元无脉冲输出.根据获得的实验数据进行线性拟合,从图中可以看出,拟合后的曲线与ReLU 神经元的输出-输入关系具有相似性,经过归一化处理,本文神经元的输出频率(frequency,F)和VIN的关系可模拟ReLU 神经元,用于基于转化法的脉冲神经网络的推理过程.此外,从图6(b)的振荡电压输出曲线中可以获得忆阻器的VTH和VH信息,即VTH对应于输出曲线的波峰,而VH对应于输出曲线的波谷,二者的统计结果如图6(d)所示.可以看出,随着VIN的增加,VTH有下降趋势,而VH基本保持不变.但直流测试发现,VTH和VH为忆阻器的内在特征,并不受扫描电压的影响.针对柔性忆阻器神经元电路的F-VIN线性依赖关系和VTH在脉冲操作模式随着VIN的增加而下降这一现象,本文从柔性忆阻器的工作机制入手做进一步地分析.

图6 柔性忆阻器脉冲神经元在不同输入电压强度下的频率调制特性 (a) 整流线性单元对应的神经元输入输出关系;(b) 柔性忆阻器脉冲神经元在不同输入电压下的脉冲输出特性,内插图为虚框内的脉冲输出放大图;(c) 不同输入电压下的输出频率统计及线性拟合;(d) VTH 和VH 在不同输入电压下的统计Fig.6.Frequency regulation characteristics of flexible spiking neuron under different input voltage intensities:(a) Input and output relationship of neuron corresponding to rectified linear unit;(b) output characteristics of the flexible memristive spiking neuron under different input voltages,and the inset is the zoom in details of the output curves in the dashed windows;(c) output frequency statistics and linear fitting under different input voltages;(d) VTH and VH statistics at different input voltages.

4 机制分析与模型建立

4.1 电子传输机制

为解释柔性神经元的频率F和器件VTH随输入VIN变化的关系,首先对柔性忆阻器的电子传输机制进行分析.如图7(a)所示,将器件发生阈值转变之前的I-V曲线在双对数坐标下进行线性拟合可以发现,当扫描电压小于等于0.2 V 时,I-V曲线拟合的斜率约为1.05,说明在此段电压范围内,电子传输符合欧姆传导机制[29].当电压大于0.2 V,即对应的电场强度(electric field intensity,E)大于4 MV/m 时,如图7(b)所示,ln(I/E)对E1/2具有线性依赖关系,表明在此电压范围内,电子传输由Poole-Frenkel(PF)传导机制主导[30].基于以上分析,对两种传输机制下的电子激活能进行了计算,分别如图7(c),(d)所示.在变温测试中,分别提取了0.1 V 和0.6 V 所对应的电流数据,并根据Arrhenius 公式对ln(I)和1000/T的关系进行了线性拟合,从中得到欧姆传输机制和PF 传输机制下的电子激活能Eae和Ea分别为(0.2237±0.02)和(0.2251±0.05) eV,其中±0.02 和 ±0.05 eV 的误差由器件的差异和读取电压选取的不同引起,可为后续仿真模型的建立提供参考.

图7 柔性忆阻器的电子传输机制分析 (a) 阈值转变前I-V 曲线在双对数坐标下的线性拟合;(b) 阈值转变前ln(I/E)和E1/2 的线性拟合;(c) 欧姆传输机制下ln(I)和1000/T 的线性拟合;(d) Poole-Frenkel 传输机制下ln(I)和1000/T 的线性拟合Fig.7.Analysis of electron transport mechanism of flexible memristor:(a) Linear fitting of I-V curve in logarithmic coordinates before threshold switching;(b) linear fitting of ln(I/E) and E1/2 in logarithmic coordinates before threshold switching;(c) linear fitting of ln(I) and 1000/T under ohmic conduction;(d) linear fitting of ln(I) and 1000/T under Poole-Frenkel transport mechanism.

4.2 核壳模型与阈值转变机制

根据已有研究报道[31-33]可知,NbOx基忆阻器在电压模式下进行电激活会形成细丝通道,随后在此区域内完成阈值转变过程.基于此,本文构建了如图8 所示核壳模型并结合电子传输机制对器件的工作机制进行了分析.在该模型中,未经任何电学操作的NbOx薄膜内部电学性质均一,由Nb2O5—x构成,如图8(a)所示;而经过电激活操作后NbOx薄膜由Nb2O5—x壳层区域和相对导电的NbO2细丝区域构成,如图8(b)所示.根据电子传输机制分析,由电场和热激发主导的PF 机制可在高电场和焦耳热的辅助下产生电流突增,因此本研究组认为该机制主导了细丝区域的电子传输并结合牛顿冷却定律[34]引起了器件的阈值转变行为,这与以往的报道结果一致[30,35].其中,由PF 机制主导的细丝区域的电阻可简记为RPF,其公式为

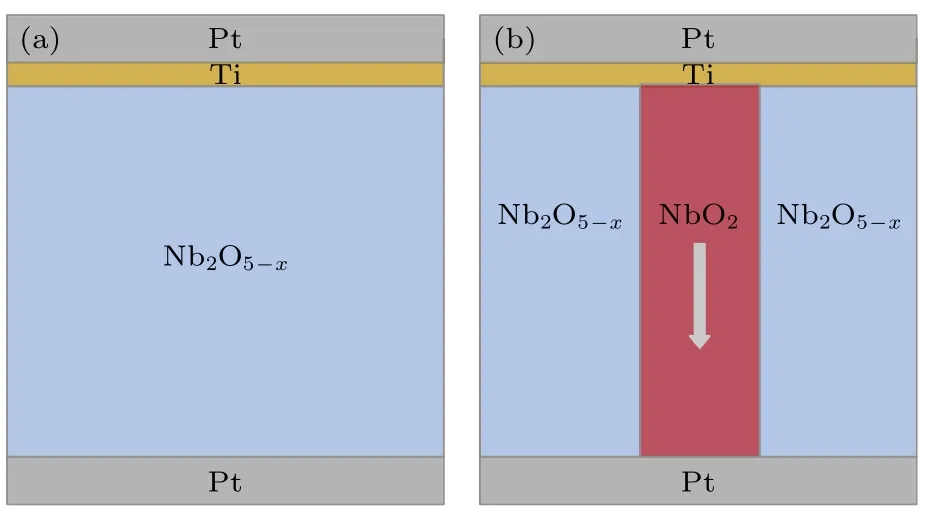
图8 核壳模型 (a) 电激活操作前的器件结构示意图;(b) 电激活操作后的器件结构示意图,其中NbOx 介质层由NbO2 细丝区域和Nb2O5—x 壳层区域构成Fig.8.Core-Shell mode:(a) Schematic diagram of the memristor before electroforming;(b) schematic diagram of the memristor after electroforming,in which the NbOx dielectric layer consists of NbO2filamentary region and Nb2O5—x shell region.

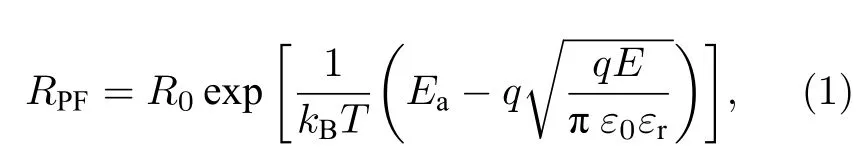
其中,R0为前置因子,Ea为电子激活能,E为电场强度,T为温度,kB为玻尔兹曼常数,ε0和 εr分别为真空介电常数和相对介电常数.由牛顿冷却定律主导的热传导公式为

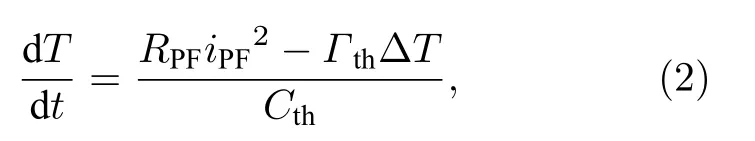
其中,iPF为流过细丝区域的电流;Гth为有效热导率,其倒数为有效热阻Rth;Cth为热容;ΔT=T—Tamb,为细丝区域与环境温度Tamb之间差值.另外,考虑到壳层区域面积相对较大,且在电场作用下也会产生漏电流,因此本研究组认为在低电场下的漏电流主要来自于壳层电阻的贡献,并由欧姆机制主导:J～Eexp(—Eae/(kT)[36],其中J为壳层区域的电流密度,E为壳层区域电场,Eae为电子激活能,T为壳层区域温度.该壳层区域的电阻可记作ROhm,其表达式为

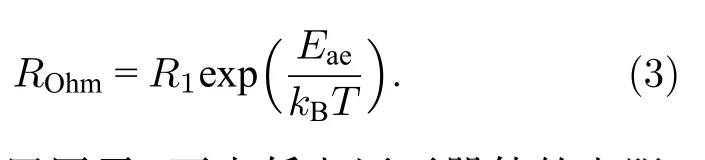
其中,R1为前置因子,可由低电压下器件的电阻-温度曲线确定.

4.3 SPICE 电路仿真

为了验证提出机制的合理性,基于以上分析进行了电路仿真(simulation program with integrated circuit emphasis,SPICE).仿真电路的组成如图9所示,其中图9(a)为细丝区域电阻(表示为Rpf)及其热传导的仿真原理图[37],图9(b)为忆阻器的工作原理图,其中顶、底电极的电阻分别表示为Rte(～350 Ω)和Rbe(～350 Ω),壳层区域的电阻表示为Rohm,拟合参数见表1.柔性忆阻器在直流电压扫描下的仿真结果如图10(a)所示,从图中可以看出,仿真曲线与实验曲线具有良好的一致性,说明构建的SPICE 模型具有合理性.

图9 基于NbOx 忆阻器的SPICE 仿真原理图 (a)细丝区域的电阻和热传导仿真原理图;(b) 忆阻器的SPICE 仿真模型Fig.9.Schematic diagram of SPICE simulation based on NbOx memristor:(a) Resistor and heat conduction simulation of filament region;(b) SPICE simulation model of memristor.

图10 柔性忆阻器及神经元的仿真结果 (a)忆阻器在直流电压扫描下的I-V;(b)忆阻器脉冲神经元在阶梯电压下的输入输出曲线;(c)神经元在不同输入电压下的输出频率统计;(d)神经元在不同输入电压下阈值电压和保持电压统计Fig.10.Simulation results of flexible memristor and neuron circuit:(a) I-V curve of memristor under DC voltage sweep;(b) input and output curve of memristive spiking neuron at stepped voltage pulses;(c) output frequency statistics of neuron under different input voltages;(d) threshold voltage and hold voltage statistics of neuron under different input voltages.

表1 用于SPICE 仿真的参数列表Table 1.Parameter list for SPICE simulation.

基于忆阻器的SPICE 模型和图5(a)所示的神经元电路,对图6 所示的神经元电路在不同输入电压(VIN)下的输出特性进行了仿真.根据实验结果(图6(d))可知,VTH随着VIN的增加有下降的趋势,这一变化与以往报道中NbOx忆阻器VTH随着温度的变化关系类似[28].在本工作中,考虑到细丝区域工作过程中产生的焦耳热对壳层的贡献以及柔性衬底的散热性能的影响,引入了温度修正项:Tc=3.3×VIN—13.2 对壳层温度进行了修正.修正公式由实验结果拟合得出,修正后壳层的温度为T+Tc.引入温度修正项后对神经元的输出特性进行仿真,得到了如图10(b)所示的振荡输出曲线,其中RL和C的值分别为30 kΩ 和1.15 nF(考虑了实际电容值有测试偏差),该仿真结果与实验具有高度的一致性,对其输出频率(F)、波峰(VTH)和波谷(VH)值进行统计,得到了如图10(c),(d)所示的统计图.从图10(c)中可以看出,随着VIN的升高,神经元的输出频率F线性增大,与实验结果一致.此外,从图10(d)中可以看出,VTH随着温度的升高逐渐下降,而VH基本不变,这一变化规律也与实验数据匹配.由此说明,基于核壳模型、PF 传导、欧姆传导以及热传导公式建立的SPICE模型具有合理性,可对柔性忆阻器和基于此构建的神经元的电学行为进行解释,为神经元的应用和硬件设计提供指导.

5 基于柔性神经元的脉冲神经网络

与已报道的忆阻器脉冲神经元[24,26,28]相对比,本文工作中基于柔性忆阻器构建的神经元电路具有更好的F-VIN线性度,能够更好地模拟神经网络中的ReLU 函数,以实现基于人工神经网络(artificial neural network,ANN)转换的SNN 系统.为验证其应用能力,构建了如图11(a)所示的转换脉冲神经网络来执行数字手写体识别任务.该网络共三层,分别为包含784 个神经元的输入层、包含100个神经元的隐含层和包含10 个神经元的输出层.训练过程采用ANN 中的反向传播算法(backpropagation,BP),隐含层和输出层分别使用ReLU 和Sigmoid 激活函数.在推理过程中则采用SNN 模式,输入为脉冲频率信号,所有激活函数用所构建的柔性忆阻器基脉冲神经元(flexible memristive spiking neuron,FMSN)实现.在本工作中FMSN利用了电容器的充放电过程和忆阻器的阈值转变特性来产生持续振荡,如果输入为脉冲形式,那么输入频率越大,充电过程越快,输出频率越高.类似地,对于固定的输入频率,脉冲幅值越大,输出频率越高.因此在SNN 中,不仅可以用脉冲脉率对输入编码,也可以通过单脉冲幅度或时间关系编码,而基于频率和幅度编码的SNN 均可以利用本文的神经元来实现.图11(b)展示了最终的识别结果,利用FMSN 所构建的SNN 可以实现95.6%的识别率,与理想情况下的ANN 结果相当(96%),表明FMSN用于神经形态计算中线性整流单元的可行性,有利于实现高性能的转换SNN 系统.

6 结论

本文制备了一种NbOx基柔性忆阻器,该器件具备稳定的阈值转变特性和良好的弯折特性,其中最小的弯折半径可达1.5 mm,弯折次数可达104次.基于柔性忆阻器,构建了脉冲神经元电路,该电路具备阈值发放、“全”或“无”和不应期等神经元放电特征,能够将模拟的输入信号转化为脉冲输出,并应用于人工感受系统的传入神经元.为验证该器件特性和电路行为的合理性,构建了由Poole-Frenkel传输机制和欧姆传输机制主导的核壳模型,用来解释忆阻器的工作机制,并通过SPICE 电路仿真对器件机制和电路放电特性进行了验证.此外,该神经元的频率-电压调制特性具有ReLU 函数相似性,可用来模拟神经形态系统中的ReLU 激活函数,实现非线性转换功能.最后,基于此神经元搭建了基于转换法的SNN 网络,在MNIST 手写体数据集上实现了95.6%的识别率,与理想ANN识别率相当.本文为柔性脉冲神经元的设计提供了参考,为其在柔性智能感知系统及神经形态计算方面的应用奠定了基础.