基于模型预测的智能汽车轨迹跟踪控制

周君武，杨 航，2，覃立仁，2，梁国全

（1.东风柳州汽车有限公司；2.广西科技大学机械与汽车工程学院，广西 柳州 545000）

随着社会的发展，人们对交通工具的要求越来越高，因此汽车的智能化发展是必然趋势。轨迹跟踪作为智能汽车的关键技术，国内外学者对其进行了大量研究，目前主要的轨迹跟踪控制算法有纯跟踪控制、前轮反馈控制、线性二次型调节控制、模型预测控制。纯跟踪控制根据预瞄朝向和预瞄点的距离来计算转弯半径和前轮转角，但是该方法在系统的稳定性和跟踪性能上很难平衡。Stanley控制核心思想是基于前轮中心的路径跟踪偏差量对方向盘转向控制量进行计算，相较于纯跟踪控制更适用于较高速场景，但是跟踪精度仍然不高。线性二次型调节控制和模型预测控制是结合车辆模型和优化理论的控制方法，近年来在自动驾驶领域得到了广泛的应用，具有较高的跟踪精度，其中模型预测控制相较于线性二次型调节控制可以添加更多的约束条件，具有更好的跟踪效果。本文建立基于模型预测控制的轨迹跟踪控制器，对模型预测控制在智能汽车上的应用做了一些仿真研究。

1 车辆运动学模型

车辆运动学模型从几何学角度研究车辆的运动规律，包括车辆的空间位姿、速度等随时间的变化。当车辆在良好路面上低速行驶时，一般不需要考虑车辆的操纵稳定性等动力学问题，此时基于运动学模型设计的路径跟踪控制器具备可靠的控制性能。

描述车辆的运动通常涉及惯性导航系统所使用的惯性坐标系XOY和描述车体相对运动的车体坐标系xoy，如图1所示。本文定义惯性坐标系的X轴指向东，Y轴指向北；定义车体坐标系x轴为车辆前方，y轴指向车辆左侧；定义车辆横摆角φ为车体坐标系x轴与惯性坐标系X轴之间的夹角，逆时针为正。

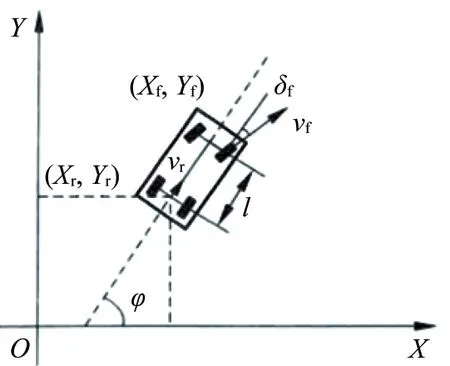
图1 车辆运动学模型

我们首先定义（X，Y）和（X，Y）分别为车辆前轴中心和后轴中心在惯性坐标系下的坐标，V为车辆在后轴中心处的速度，l为轴距，R为后轴中心的瞬时转向半径，ω为车辆横摆角速度，δ为前轮偏角。

在后轴行驶轴心（X，Y）处，速度为：

前后轴的运动学约束为：

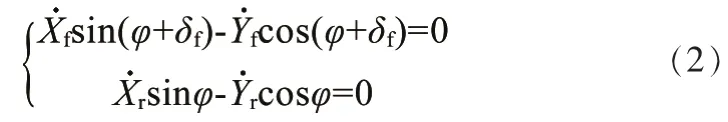
由式（1）和（2）可得：

根据前后轮的几何关系可得：

由式（3）和（4）可得横摆角速度为：

由ω和车速V可得到转向半径R和前轮偏角δ：

由式（3）和（5）可得到车辆运动学模：

为了使公式统一规范化，我们使和为惯性坐标系下车辆在X轴和Y轴的速度，v为车辆后轴中心速度，则运动学模型为：

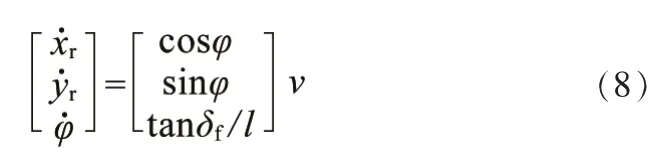
车辆运动学模型可看做一个输入为u（v，δ）和状态量为X（x，y，φ）的控制系统。其一般形式为：

假设参考系统已经在期望路径上完全通过，得到路径上每个时刻的状态量和控制量，对于参考系统每一时刻的状态量和控制量满足：

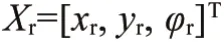
对系统一般形式在任意点处进行泰勒展开，只留一阶项，忽略高阶项，得到：

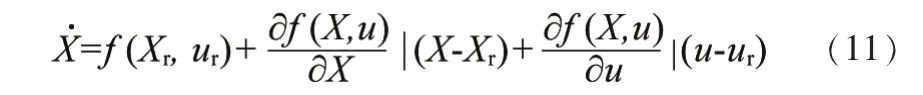
将式（11）和（10）两式相减得到：

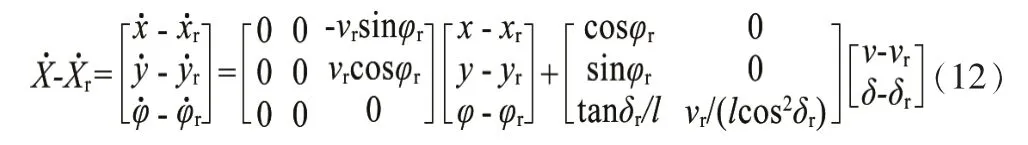
由上述可得：

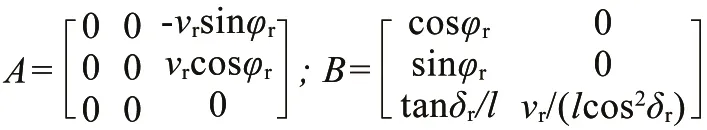
向前欧拉离散化可得：

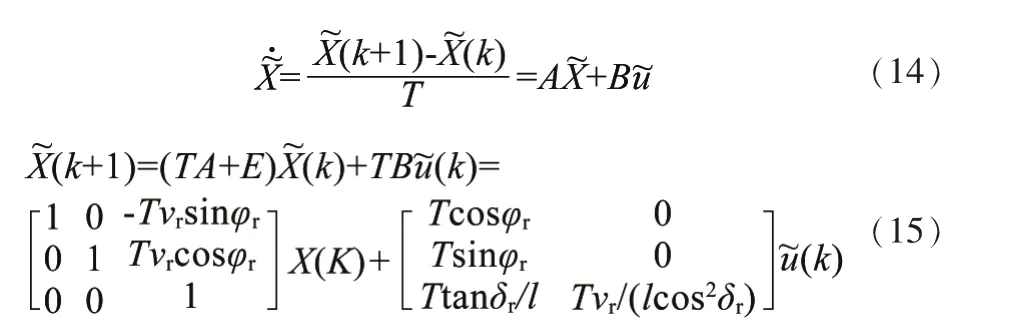
式中：T——采样时间。

2 目标函数设计

目标函数的设计应该使得智能车辆能快速平稳地跟踪参考轨迹，因此，我们对系统的状态误差和控制增量误差求和，使其取最小值，同时为了使目标函数便于转换成标准二次型规划进行求解，设计如下目标函数：

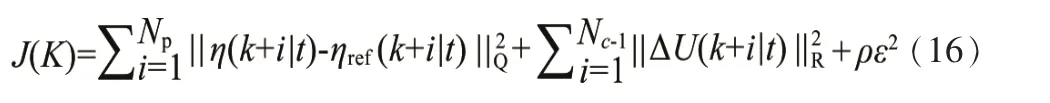
式中：N——预测时域；N——控制时域；Q、R——权重矩阵；ρ——权重系数，ε——松弛因子。其中，第一项反映了系统对参考轨迹的跟随能力，第二项使得系统的控制过程更加平稳，第三项为软约束，保证目标函数可以得到可行解。

由式（15）可得：

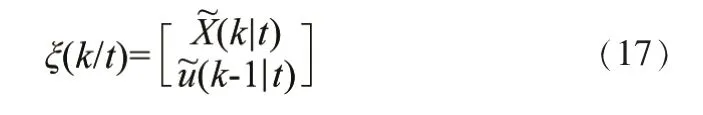
可构造新的状态空间：

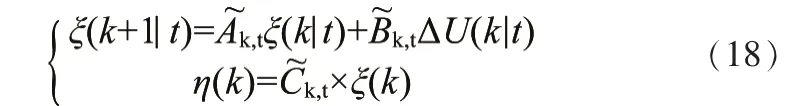
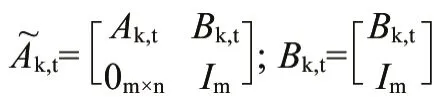
为了使计算简化，假设：

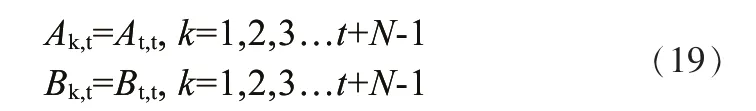
经过推导计算可得系统的预测输出表达式：

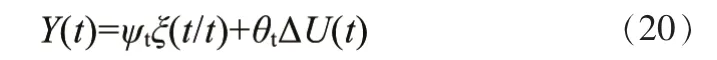
式中：

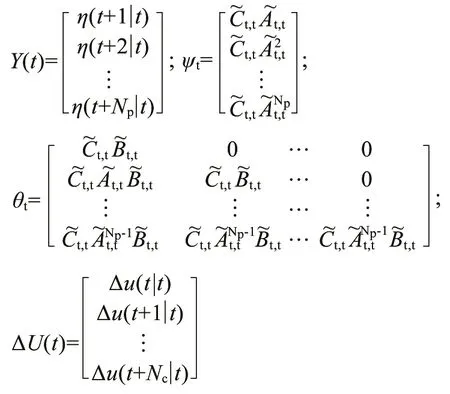
3 约束条件设计

本文在此对控制量极限和控制增量进行约束，控制量约束为：

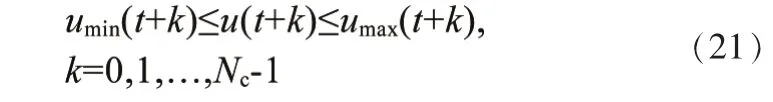
控制增量约束为：

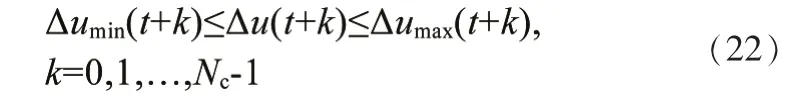
在每一周期对目标函数进行求解后，得到控制时域内的一系列控制输入量：

将该控制序列中第一个控制增量作为输入作用于系统，即：

进入下个控制周期后，重复上述过程，如此循环实现了对车辆的轨迹跟踪控制。

4 Matlab/Sim ulink仿真

首先在Simulink中搭建运动学模型，然后将其封装，建立基于运动学模型（图2）和模型预测控制的轨迹跟踪器（图3）。

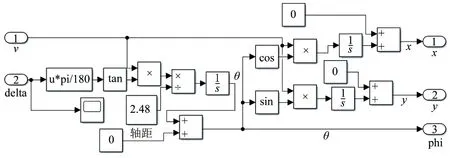
图2 Simulink运动学模型

图3 轨迹跟踪器模型

这里采用五次多项式工况，对模型预测控制与Stanley控制的跟踪效果进行仿真对比。如图4、图5所示。

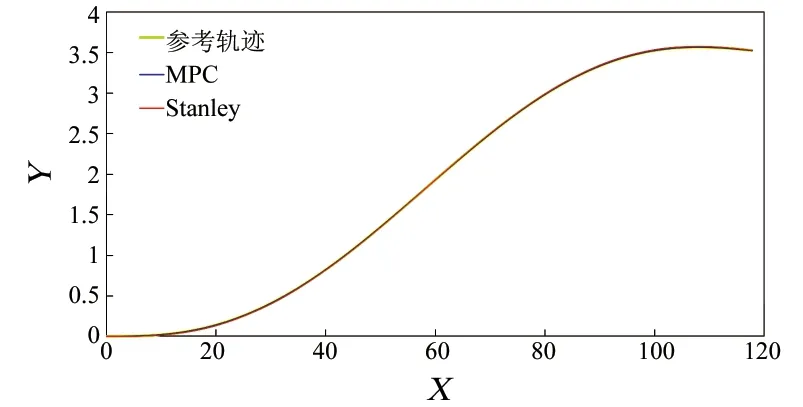
图4 轨迹跟踪结果

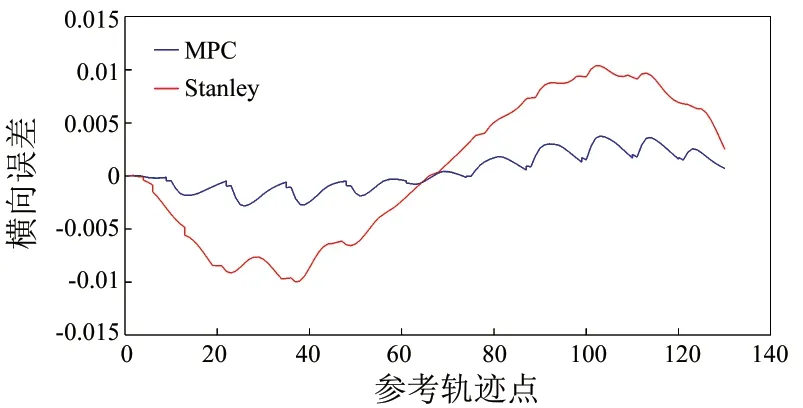
图5 横向误差对比

由仿真结果可知，当速度为20m/s时，建立的基于运动学模型和模型预测控制的轨迹跟踪器的横向误差在-0.005~0.005之间，能够准确地跟踪期望轨迹，而Stanley控制的横向误差最大超过0.01，跟踪效果较差。因此与Stanley控制相比，模型预测控制的跟踪精度更高，横向误差更小。

5 结语

本文建立了车辆运动学模型，在Matlab/Simulink仿真平台上验证了基于模型预测控制的轨迹跟踪器在速度为20m/s、五次多项式工况下的轨迹跟踪效果良好，为模型预测控制在智能汽车上的发展垫定了一定基础。