基于强化学习的机器人智能路径规划*
谢文显,孙文磊,刘国良,徐洋洋
(新疆大学机械工程学院,乌鲁木齐 830047)
0 引言
随着工业4.0逐步普及,各制造工厂都依靠自动化生产线逐渐实现智能化。为降低生产成本、提高焊接的效率和精度、减轻作业的强度和风险,人工焊接已基本被焊接机器人所取代。而作为降低成本和提高效率的前提,对焊接路径进行合理的规划必不可少。目前,对焊接机器人路径规划的研究大都在算法上进行改进来缩短路径规划的时间,这些算法可大致分为传统路径规划算法,如A*算法、D*算法、RRT算法等;以及仿生智能路径规划算法,如遗传算法(GA)、果蝇优化算法(FOA)、粒子群算法(PSO)等。孙灵硕[1]运用改进的RRT-Connect算法,有效地避免了随机树在路径搜索过程中陷入凹形障碍区域所造成的算法性能下降的问题。裴跃翔等[2]引入一种结合模拟退火算法的筛选操作来改进基本遗传算法,增强算法局部搜索能力,改善了GA容易陷入局部最优、搜索过程比较慢以及效率低下的问题。姚江云等[3]提出改进人工蜂群算法,用Lévy (莱维) 分布代替侦查蜂寻找新蜜源的过程中原有0~1之间的随机分布,使焊接机器人在较短的时间内搜索到全局最优路径。
虽然上述算法已经发展的较为成熟,但它们只能规划出固定场景下的最优路径,当机器人所在环境发生变化后,机器人需要重新认识环境后才能进行路径规划,这无疑会消耗大量的时间。针对现实中机器人在应用时所面对的多变的环境,若能让机器人通过训练学会某种策略,使其即使面对全新的环境也能直接进行路径规划,不仅会增加机器人的适应性,还能节省大量的人力物力资源,进而提高工作的效率。强化学习的出现和迅速发展让这成为了可能。不同于监督学习,强化学习是一种在基本没有先验知识对智能体的动作选择进行指导的情况下,让智能体从一开始什么都不会,通过不断尝试,从错误中学习,最后找到规律,学会到达目标的方法。近年来,将深度学习与强化学习相结合已成为一种趋势,二者融合而成的深度强化学习算法与改进的智能算法相结合后逐渐广泛应用在各种机器人上,包括移动机器人的路径规划[4-5],无人机的自主导航与任务分配[6-7],机械臂的操控[8]以及实际生产线上的人机协作问题[9]等。
本文提出一种基于强化学习的机器人路径规划策略,让机器人能自主运用所学会的策略,控制其末端从焊缝起点到终点的过程中,能尽可能的沿着焊缝的中心线运动,且在面对全新的测试轨道中,也依然能顺利完成路径规划任务。
1 机械臂路径规划模型构建
针对当下各种接焊方式中应用广泛的的对接接头,由于受到仿真软件的局限,将焊缝模型按图1所示简化为曲线型的轨道模型,并用ur5六轴机械臂代替焊接机器人进行研究。
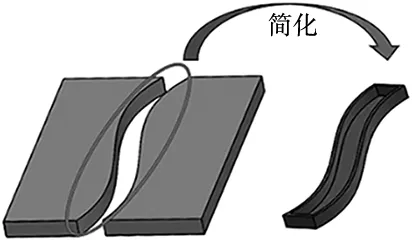
图1 对接接头及焊 缝简化模型
本文中,ur5机械臂在未知的轨道环境中,通过与环境的交互来确定最优策略,使其从轨道的起点到终点的过程中尽可能靠近中线,获得最大的回报值。可用马尔可夫决策过程(markov decision process,MDP)来对该研究问题进行建模,MDP的动态过程如图2所示。

图2 MDP动态过程图
智能体的初始状态为s0,通过策略π0执行动作a0后转移到下一个状态s1,并从环境中获得回报值r0。随后在新的状态s1,智能体采取新的策略与环境持续交互直至到达目标状态sT,在该过程中智能体会累积得到一系列的回报(r0,r1,…),可用式(1)来表示累计回报:
(1)
式中,γ∈[0,1]为折扣因子,用来权衡未来回报对累积回报的影响。整个模型的构建主要包括状态、动作、策略和奖励4个要素。
1.1 模型的状态
作为智能体的ur5机械臂的末端装有激光雷达,激光雷达向自身360°范围内射出360条激光线,相邻激光线之间均间隔1°,每条激光线都会测量并返回一个该方向障碍物的距离数据。机械臂每次执行动作后会改变激光雷达的位姿,其所测得的各个方向的激光数据也会发生相应变化,因此可以用测得的激光数据所组成的列表来描述模型的状态。但为了减少智能体的训练时间,加快学习效率,可适当的删去不必要的数据输入。最后选择以激光雷达的正前方作为基准,向左、右各偏转120°范围内的共240个激光数据作为整个系统的输入状态,如图3所示。

图3 激光雷达示意图
图3中黑色的圆为激光雷达,浅灰色箭头为此时激光雷达的正前方,240°范围内的共240条激光线测得的激光数据所组成的列表st=[L0,L1,…,L238,L239]t就是模型在t时刻的状态,各个时刻的状态st共同组成了模型总的状态S。
1.2 模型的动作
在整个模型中,机械臂执行动作后本质上改变的是其末端激光雷达的位姿,只要确定好执行动作后激光雷达运动后的位姿,再通过运动求解器反解出ur5机械臂到达指定位姿时各关节的角度,即可让机械臂运动到指定的位置。因此可以利用激光雷达的位姿变化来设置模型的动作,每次执行动作后,激光雷达位姿的变化包括3个方面,分别为x轴方向上的坐标变化Δx,y轴方向上的坐标的变化Δy和z轴方向上的偏转角度θi。
本文以激光雷达的正前方作为基准,偏转角度θi的范围从-18°~+18°,每个θi均间隔Δθ=3°,总的角度范围θ=36°。即i为整数,取值范围为[0,12],共有13个θi值,分别对应a0~a12共13个动作,如图4所示。
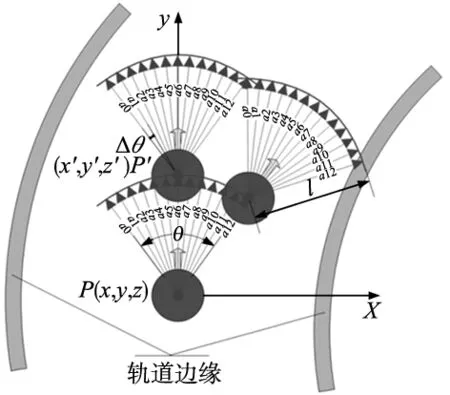
图4 模型动作示意图
图4中黑色的圆代表激光雷达,圆上的13个箭头对应13个动作,机械臂通过策略选择动作并执行后,机械臂末端的激光雷达的位移步长为l,即从点P(x,y,z)运动到点P′(x′,y′,z′),然后在P′处继续选择新的动作并位移l后到达下一个位置,如此循环直到抵达终点。最终通过多次的学习和训练,机械臂找到最优的策略使得从起点到终点的途中,其末端的每一个位置点坐标P(x,y,z)都尽可能的处于轨道的正中间。点P和点P′坐标间的关系符合式(2)。
(2)
1.3 模型的策略与奖励
模型的策略π表示从状态集合S到动作集合A的映射,是智能体选择动作的依据,也是本文的重点研究对象。本文利用强化学习算法,通过搭建神经网络来拟合策略π,最终通过寻找最优的神经网络参数来确定最优的策略。此外,在强化学习中,算法能否收敛以及收敛的程度和快慢与奖励函数R的设置紧密相关。在下一章中,本文将根据选择的强化学习算法对模型的策略和奖励设置进一步说明。
2 基于深度Q网络的机械臂路径规划自主决策
在前文模型构建中提到,策略π这一要素通过强化学习(reinforcement learning,RL)求得,而奖励R这一要素也需根据所选取的RL的具体算法来设置。策略π和奖励R之间是相互关联的,可构造一个函数来描述二者间的关系,该函数成为值函数。值函数也叫评价函数,通常用Qπ(s,a)表示,是指智能体在当前状态s0下,一直遵循策略π,选择并执行一系列的动作a转移至目标状态sT的这一过程中,通过式(1)所计算的累积加权奖励值的数学期望,其表达式为:
(3)
而强化学习最终的目标则是找到最优的策略π*,使得值函数最大,用Q*(s,a)表示最优值函数,其表达式如下:
(4)
且最优值函数遵循贝尔曼最优方程,即:
(5)
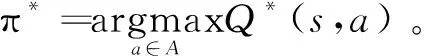
2.1 基于改进DQN的决策算法
针对原始的DQN算法中存在的过估计以及在经验回放时采用均匀分布采样而不能高效利用数据的问题,引用Double DQN(DDQN)[12-13]的方法来消除过估计,利用优先经验回放(prioritized replay)的策略[14]来打破均匀采样,赋予学习效率高的状态以更大的采样权重。改进后的DQN算法流程如图5所示。
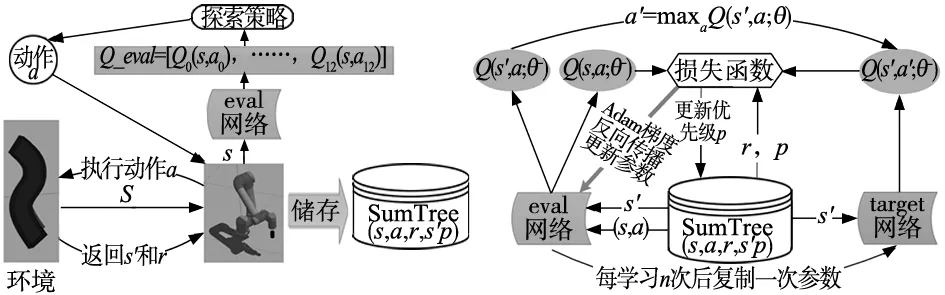
(a) 经验样本储存流程 (b) 参数训练与更新流程
由图5可知整个算法的训练流程可分为两部分,其中图5a为储存经验样本的过程,目的是实现改进后算法的优先经验回放机制。具体做法是:机械臂通过末端的激光雷达从轨道环境中测出激光数据,从而获得当前的状态s,将状态s输入eval网络后输出由13个动作的Q值所组成的列表Q_eval,接着通过探索策略确定执行的动作a。机械臂执行动作a后,其末端的激光雷达到达新的位姿,进而得到此时的状态s′。同时,根据设置的奖励函数,机械臂在该过程中会获得一个奖励r。将当前状态s,选择的动作a,得到的奖励r和下一个环境信息s′作为经验(s,a,r,s′),并赋予其一个优先级p(每个样本最初赋予的优先级均为1,在训练的过程中优先级会进行更新)。将样本ei=(s,a,r,s′,p)用SumTree这样的二叉树结构进行储存,在后续训练时,每次从SumTree中按样本的采样概率选取m个样本[e0,e1,…,em-1]作为一个批次,使用随机梯度下降算法来更新eval网络的参数。
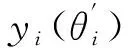

(6)
即先在eval网络中先找出最大Q值对应的动作,然后利用这个动作在target网络里面计算目标Q值。通过最小化当前Q值和目标Q值之间的均方误差(也就是损失函数)来更新网络参数θ,损失函数为:
(7)
用Adam算法梯度反向传播来更新eval网络的参数θ:
θi+1=θi+α▽θiLi(θi)
(8)
式(7)中ωi为样本i的优先级权重,其计算式为:
ωi=(N*P(i))-β/maxk(ωk)
(9)

(10)
对eval网络参数进行了梯度更新后,|δi|会重新计算,样本的优先级pi也会在SumTree上更新。
2.2 神经网络的结构
前文中提到eval网络和target网络的是两个结构完全相同的神经网络,神经网络中不断更新的神经元参数就是最终要找的策略。而神经网络的层数是否合理,每层网络中的神经元个数又是否合适与最终能否找到最优策略息息相关。本文研究中,用一个包含输入层、输出层和3个隐藏层的共5层的神经网络来拟合输入状态和输出动作间的控制策略,网络结构如图6所示。
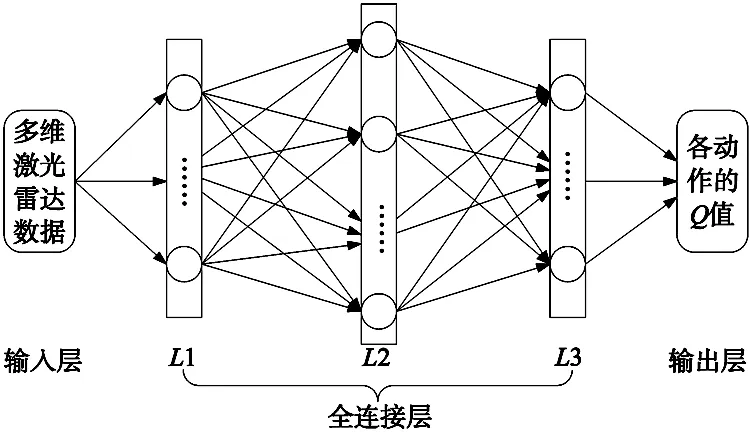
图6 神经网络结构图
其中输入层为机械臂末端的激光雷达所采集的240维激光数据;L1~L3均为隐藏层,分别是由248,500和248个神经元组成的全连接层,用于训练和存储网络参数;输出层则为13个动作所对应的Q值,可表示为[Q(s,a0),Q(s,a1),Q(s,a2),…,Q(s,a12)]。
2.3 探索策略
要想获得最大的累积回报,平衡好“探索”与“利用”的关系不可或缺,故探索策略的选择也尤为重要。贪心策略(ε-greedy)[15]是一种常用的探索策略,该策略让智能体在通过决策选择动作时,有一很小概率ε(<1)随机选择一个未知的动作,而以剩下1-ε的概率去选择已有动作中值函数最大的动作。这样做既能避免智能体因过度“探索”未知策略而获得大量的负样本,导致其难以到达目的地而花费大量的训练时间;又能防止智能体因过度“利用”现有的最优策略来选择Q值最大的动作而陷入局部最优。本文采取ε递减式的贪心策略:先赋予ε较大的值,使机器人在训练初期具有足够的探索能力,积累足够的新的学习样本;接着在训练过程中让ε逐渐减小,这样能让机器人在训练的中后期变得越来越“保守”,增加选择Q值最大的动作的概率,尽快到达终点,节约训练时间;当ε减小至0.05后就保持不变,即让机器人至少留有5%的概率用于探索,防止过拟合。
2.4 奖励函数
奖励函数首先应满足最基础的条件:当机械臂的末端到达指定的终点时获得一个正向的奖励,而偏离轨道中心一定范围后则给与相应的惩罚。但为了避免在训练初期,机械臂因长期到达不了终点、获得不到正向奖励而陷入局部最优的情况,本文提出奖励累积的方法来牵引机械臂向终点方向运动;同时,为了让机械臂的末端在执行每一个动作后都能尽可能的靠近中线,再额外加入一个反馈奖励gap来加以调节,以此来加快训练的速率和效果。奖励函数R设置如式(3)所示,其表明机械臂在状态st的奖励为执行完动作at后的即时奖励加上0.9倍的上一个状态st-1的奖励。

(11)
式中,r(st,at)为机械臂执行动作后的即时奖励,当机械臂末端到达轨道终点时,给与+100的奖励,本次训练周期结束,机械臂回到起点;当机械臂末端偏离轨道中线的距离超过设定的阈值d时,给与-100的惩罚,且机械臂回到轨道的起点。其它情况下,式中gap为每次执行动作后机械臂末端偏离轨道中心线的距离的绝对值,gap越小则相当于减去的惩罚值越小,以此来让机械臂末端尽量在轨道的正中央。λ为大于0的比例系数,用来调节gap所占有的比重来达到更好的训练效果。
3 仿真实验与分析
本实验基于Ubuntu系统下,用ROS和Gazebo搭建出虚拟仿真训练环境如图7所示。
仿真环境由末端装有激光雷达的ur5机械臂和由焊缝模型简化而成的轨道组成,轨道又分为一个学习轨道和3个测试轨道a、b、c。机械臂在学习轨道上进行多次学习训练后,先在学习轨道上进行从轨道起点到终点的成功率测试,在成功率满足要求后,用训练好的参数在3个未知的测试轨道上进行成功率测试。
3.1 学习轨道的训练与测试
在Pycharm集成开发环境下,用Python编写改进后的DQN算法作为机械臂的动作选择策略,再结合MoveIt!软件来控制机械臂执行相应的动作,从而达到让机械臂在轨道中进行学习训练的效果,具体的训练参数如表1所示。

表1 各项训练参数的符号与设定值
按照表1中设定的参数让机械臂在学习轨道上进行3000个周期的训练后,eval网络的训练指标变化趋势如图8、图9所示。

图8 误差损失随迭代 次数变化图图9 总奖励随训练 周期变化图
由图8可知,在训练的3000个周期内,eval网络的参数共学习迭代了6000多次。随着新的样本不断进入记忆库,误差损失loss在A点处达到至高点,之后便随着学习次数增加而逐渐减小并趋向于收敛,由此可知机械臂的训练确有实效,其决策能力越来越强。
而从图9可知随着训练周期次数的增加,每个周期获得的总的累积奖励呈三个阶段的阶梯式上升趋势。在I1阶段,机器人还不认识环境、没有决策能力,只能获得极少奖励,此时机械臂末端的路径对应图7中训练轨道的AB段;在I2阶段,机器人已初步认识环境、具备一定决策能力,能获得少量奖励,其路径对应训练轨道的AC段;在I3阶段,机器人经过多次与环境交互学习后,完全认识环境、具有很强决策能力,能到达目标点、获得大量奖励,此时机器人的路径对应训练轨道的AC段。
将训练好的神经网络参数保存后,在学习轨道上进行成功率测试,当偏离轨道中心的阈值分别设定为6 mm、6.5 mm和7 mm时,机械臂末端顺利到达终点的成功率分别为93%、97%和100%。由此可知,当按照训练时的阈值6 mm进行测试实验时,机械臂已经能良好地进行自主决策,当适当放宽阈值后,其成功率也会随着阈值的增加而增加。这是因为机械臂的运动误差和激光雷达的测量误差会干扰机械臂对环境信息的观测,使得机械臂对当前自身状态的判断不够准确而选择了非最优的动作,进而导致机械臂末端偏离轨道中心的距离超过了所设置的阈值。当逐步增加阈值时,其实是增加了机械臂对环境观测的容错率,进而提高了成功率。
3.2 测试件轨道的测试
用训练好的神经网络参数作为决策,指导机械臂在未经历过的测试轨道a、b、c上进行测试,进一步检查机械臂的学习效果,检验机械臂所学会的策略是否能完成在全新环境下的路径规划,测试过程如图10所示。
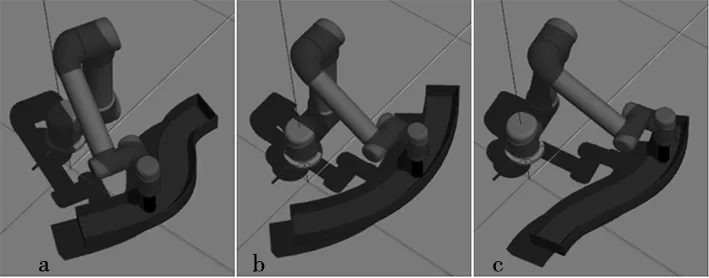
图10 测试赛道的测试过程图
在3个测试轨道上,将偏离中心的阈值分别为6 mm、7 mm和8 mm,利用所学的参数控制机械臂选择和执行动作,共进行9组仿真实验,每组实验均进行50个回合的测试。测试的成功率如图11所示,由该图可知当阈值适当放宽到8 mm后,在3个测试轨道上的成功率均可达到90%以上。
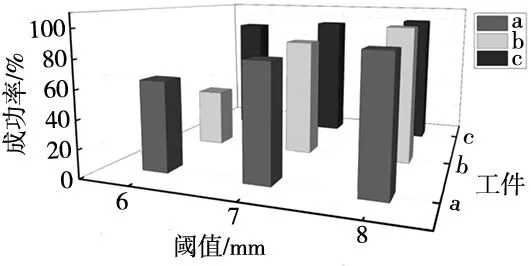
图11 测试轨道成功率变化图
机械臂在通过所学的最优策略,根据当下实时的状态选择动作从轨道的起点到终点的过程中,会经历多个路径点。可以利用MoveIt中自带的笛卡尔路径规划方法,用小的直线段依次串联起所有的路径点,形成一条连续的轨迹,然后让机械臂沿着轨迹连续地从轨道的起点到终点。设置终端步进值为0.005 m,即机械臂末端每次会位移一段0.005 m的直线段;设置跳跃阀值为0,确保规划出的路径经过每一个路径点;设置最大尝试规划次数为200,避免因偶然因素出现规划失败的情况。利用笛卡尔路径规划在测试件a、b、c上规划出的连续轨迹如图12所示,由图可知轨迹基本靠近轨道的中心。

图12 测试轨道上的轨迹图
4 结论
本文将改进后的DQN算法用于ur5机械臂来实现焊接机器人的路径规划,让机械臂通过激光雷达实时地感知环境、获取当下的状态,并根据当下的状态和学会的策略选择最优动作,使机械臂从轨道起点顺利到达终点的同时尽可能靠近轨道的中线。在Ubuntu系统下的Gazebo仿真环境中分别对机械臂进行训练和测试来验证方法的可行性和算法的有效性。先在学习轨道上进行足够回合数的训练后,将机器人学到的知识迁移到新的测试轨道上验证学习效果。仿真结果表明,机械臂通过改进后的DQN算法所学会的策略能顺利指导机械臂从轨道的起点运动到目标终点,且运动轨迹基本靠近轨道中心。
DOI:10.16383/j.aas.c190451.

