广义阻尼模型及其在混凝土重力坝地震响应分析中的应用

钱向东,李 晨,沈人杰

(河海大学力学与材料学院，江苏 南京 210098)

现代计算力学可以非常精确地分析线弹性结构的静力学问题，也能够高精度地计算质量矩阵和刚度矩阵，从而获得具有较高精度的结构无阻尼自振特性，特别是较低阶的频率和振型。然而，对于结构振动分析中不可忽略的阻尼特性，还处于简单的估算状态。常用的阻尼模型为经典的黏滞阻尼模型[1]，该模型无论是耗能机理还是试验观测都不符合混凝土、岩石、橡胶以及许多复合材料的阻尼特性[2]。具体应用时，一般近似地采用振型阻尼比或比例阻尼表示阻尼特性或建立阻尼矩阵。这种结构阻尼的表达方法忽视了其在结构动力学中的重要性。因此，为了获得可靠的结构动力响应，应该采用符合材料耗能机理的阻尼模型，把阻尼矩阵的计算精度提升到与质量矩阵和刚度矩阵同等的水平。

阻尼体现了结构在振动过程中的能量损耗，一般认为主要由机械能转化为热能后消散，也有部分可能由于引发周围介质(地基、水、空气等)的振动而逸散。如果不考虑能量逸散，则结构的能量损耗主要来自材料阻尼，可由材料的本构关系表示。事实上黏弹性、黏弹塑性材料的本构关系均可反映材料在变形过程中的能量损耗。由于黏弹性材料本构关系的多样性和复杂性，各国学者提出了诸如复常数模量模型[3]、模态应变能模型[4]、标准流变模型[5]、分数导数模型[6]、分数指数模型[7]、微振子模型[8]和广义流变模型[9]等黏弹性结构的动力分析模型，不同的动力分析模型对应着不同的阻尼模型。其中最有代表性的就是广义流变模型，该模型的阻尼力在数学上表示为速度与某一核函数的卷积，是一种非黏滞阻尼模型。当核函数为狄拉克-δ函数时，模型就退化为黏滞阻尼模型。因此，该阻尼模型又被称为广义阻尼模型[9]，目前常用的核函数有指数型、高斯型[10]等。

基于广义阻尼模型的结构运动方程是耦合的二阶积分-微分方程组。为了避免求解复杂的积分-微分方程组，通常在频率域进行求解[11-12]，在频率域构造核函数，以便获得可以实现时域逆变换的传递函数矩阵，应用范围受到了极大的限制。随着计算技术的发展和工程应用的需要，人们开始研究在时间域直接求解广义阻尼结构运动方程的方法。对于指数型核函数，通过引入状态变量消除卷积积分,在状态空间中采用直接积分法和振型叠加法进行求解[13-17]，段忠东等[18]采用精细积分大大提高了状态空间法的计算精度，钱向东等[19]将该方法应用于混凝土重力坝的地震响应分析。对于其他类型的核函数，状态空间法不再适用，于是有人尝试采用中心差分法[20]、Newmark法[21-22]和Galerkin加权余量法[23]在时间域对积分-微分方程进行直接数值积分，相关研究都是针对简单的多自由度算例开展，还未见具体的工程应用。

本文根据黏弹性材料广义流变模型的积分型本构关系，导出了具有广义阻尼模型的结构动力学方程。以Koyna混凝土重力坝为例，将广义阻尼模型应用于混凝土重力坝的地震响应分析。采用Newmark直接积分法求解积分-微分方程组，分析了松弛参数、时间积分步长对大坝地震响应的影响，同时比较了广义阻尼模型和黏滞阻尼模型情况下大坝的地震响应。

1 广义阻尼模型的结构动力学方程

混凝土、岩石材料均具有黏弹性性质，在线性、等温和初始应变ε(0)=0条件下， 其时间域内的本构关系可用广义流变模型表示为[24]

(1)

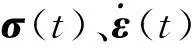
在均匀、各向同性情况下，松弛函数矩阵为

G(t)=D+ηg(t)

(2)

式中：D、η分别为弹性矩阵和黏性矩阵；g(t)为卷积核函数。则式(1)可以表示为

(3)

当η=0时，式(3)为线弹性模型的本构关系；当核函数g(t)为狄拉克-δ函数时，式(3)为Voigt-Kelvin模型的本构关系。

采用有限元对黏弹性结构进行离散，离散后结构的动力虚功原理可以表示为

(4)

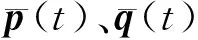
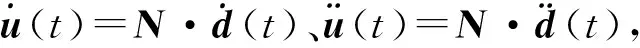
将单元的相关变量代入式(4)并考虑黏弹性本构关系式(3)，则有

(5)

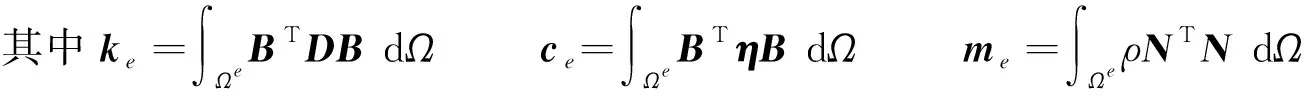
式中：ke为单元弹性刚度矩阵；me为单元质量矩阵；ce为单元黏性阻尼矩阵；fe为单元等效结点荷载列阵。

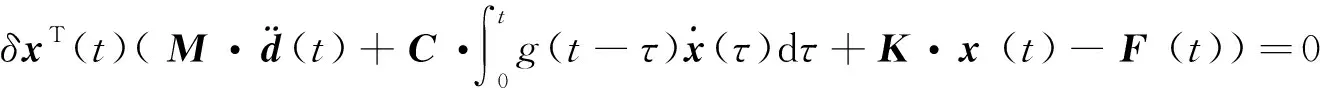
(6)

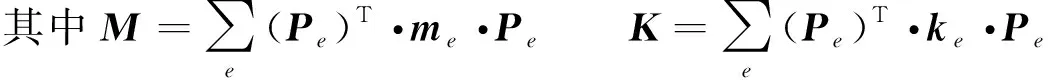
式中：M为整体质量矩阵；K为整体弹性刚度矩阵；C为整体黏性阻尼矩阵；F(t)为整体等效结点荷载列阵；δx为整体虚位移列阵。

由虚位移的任意性，可得黏弹性结构的动力学方程为

(7)

式(7)为二阶积分-微分方程组。记

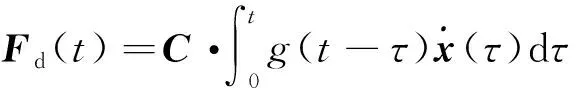
(8)

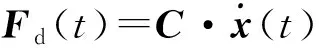
如果结构由n种材料组成，则阻尼力可以表示为

(9)

相应的结构的动力学方程为

(10)

2 动力方程的时域求解

2.1 核函数的选择

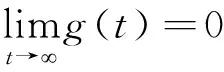
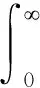
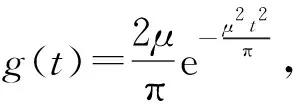
2.2 Newmark直接积分法

对于指数型核函数，由于其函数的特殊性，通过引入一组辅助变量(状态变量)，可以将积分-微分方程方程组(7)或(10)转化为一阶微分方程组[13]，再求解，称之为状态空间法。其优点是求解过程中无须计算卷积积分，但缺点是将未知量(或方程数)扩大了一倍，且不适应用于其他类型的核函数。

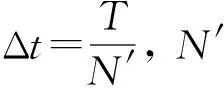
(11)

Newmark法计算格式为

(12)

其中α、β为两个计算参数，当α≥0.5、β≥0.25(0.5+α)2时为无条件稳定格式。将式(12)代入式(11)，并采用梯形法计算卷积积分，则可导出求解t+Δt时刻位移响应的方程：

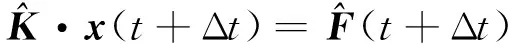
(13)

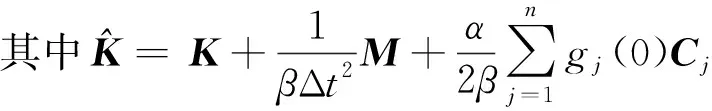
Newmark直接积分法适用于任何形式的核函数，关于算法的实现、卷积积分的讨论以及算例验证可参见文献[22]。

3 混凝土重力坝地震响应分析

本文以Koyna大坝为例，利用ANSYS有限元建模功能，采用自编的基于MATLAB的程序[22]进行大坝地震响应分析，讨论广义阻尼模型及其核函数对重力坝地震响应的影响。

3.1 计算模型

Koyna重力坝坝高103 m,底宽70 m，坝顶宽度为14.8 m，几何参数如图1所示。为了讨论和比较方便，计算时略去地基对坝体动力响应的影响，即简单地采用刚性地基模型，同时也不考虑库水的影响，以空库工况进行分析，有限元网格如图2所示。坝体混凝土材料的密度为2 643 kg/m3,动弹性模量为31 027 MPa,泊松比为0.15，各振型的阻尼比均为0.05。

图1 Koyna重力坝模型尺寸Fig.1 Model size of the Koyna gravity dam

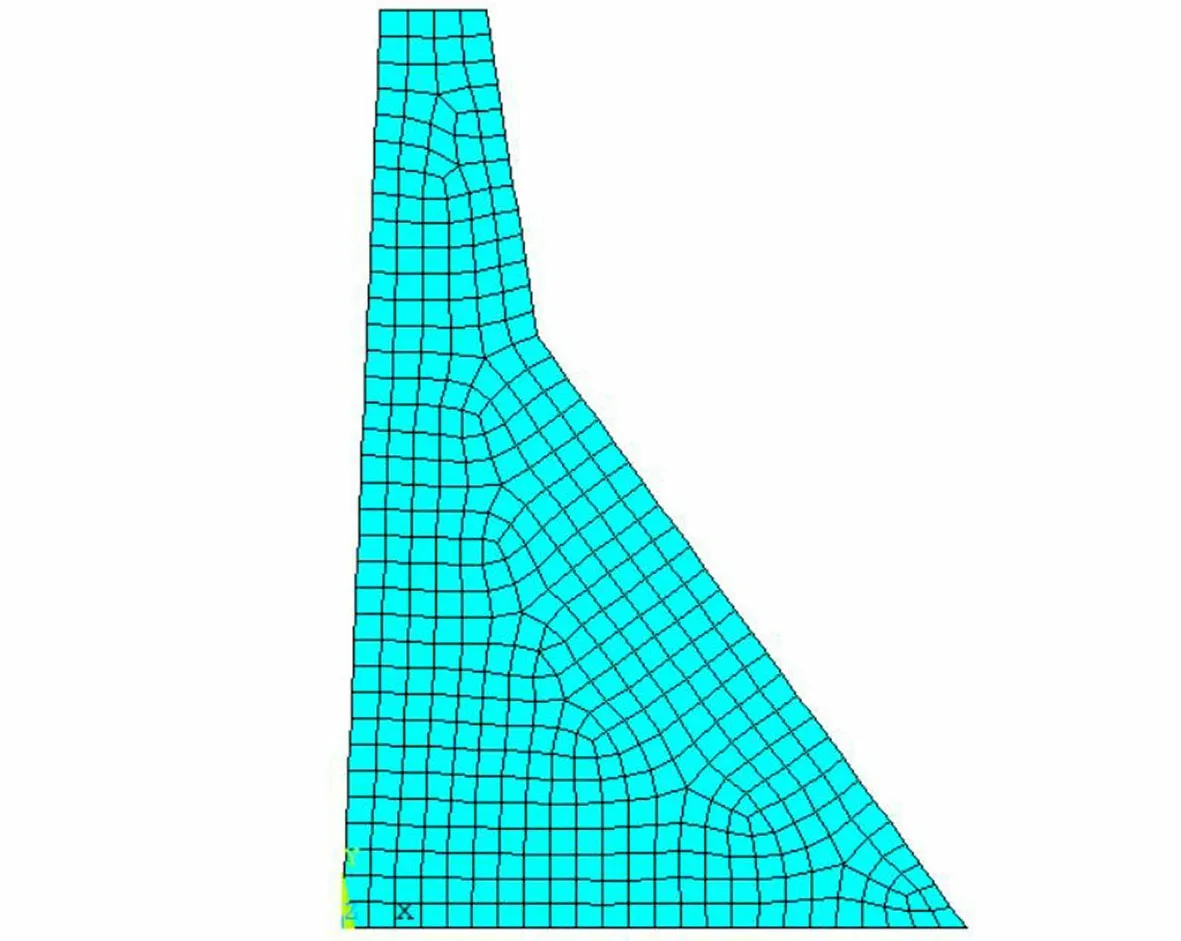
图2 坝体有限元网格Fig.2 Finite element mesh of the dam

3.2 阻尼模型与参数

设大坝由一种混凝土材料组成，采用式(8)所示的广义阻尼模型，只需一个阻尼矩阵C和一个核函数g(t)就可以表示材料的非黏滞阻尼特性。在缺乏试验资料的情况下，一般由质量矩阵和刚度矩阵的线性组合计算阻尼矩阵C=a1M+b1K，系数a1、b1由系统的两阶振型阻尼比和自振圆频率确定。由上述计算模型的自振特性分析，得到大坝的前2阶自振圆频率为20.20 rad/s和56.01 rad/s，从而可以确定a1=1.485、b1=1.312×10-4。

阻尼模型分别采用指数核函数和高斯核函数，分别称为指数型非黏滞阻尼和高斯型非黏滞阻尼。目前，关于松弛参数μ的试验资料非常少，文献[26]根据钢筋混凝土悬臂梁的锤击振动测试，识别得到μ的平均值约为104.3 s-1。为了考察μ的取值对阻尼效应的影响，本文μ分别采用70 s-1、100 s-1、130 s-1、160 s-1、190 s-1进行对比计算。为了比较，同时也采用黏滞阻尼模型进行计算。

3.3 地震波与直接积分参数

采用实测的Koyna水平向地震波(图3)作为地震输入，顺河向峰值加速度为4.647 8 m/s2，地震加速度记录时间长度为10 s，间隔0.01 s。取Newmark直接积分法参数α=0.5、β=0.25,数值积分的时间步长Δt分别取0.01 s、0.005 s、0.002 5 s。

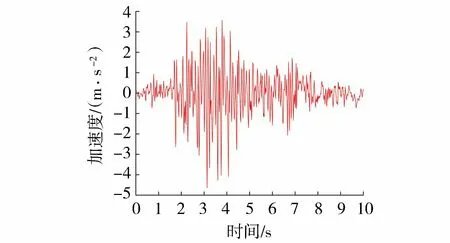
图3 Koyna水平向地震加速度Fig.3 Horizontal acceleration of Koyna earthquake

3.4 计算结果

图4和图5分别给出了Δt=0.01 s,松弛参数μ为70 s-1、100 s-1、130 s-1、160 s-1、190 s-1情况下，指数型非黏滞阻尼和高斯型非黏滞阻尼对应的坝顶水平向位移响应和加速度响应时程曲线。图6给出了黏滞阻尼模型对应的坝顶水平向位移响应和加速度响应时程曲线。

图4 坝顶水平向地震响应(指数型非黏滞阻尼)Fig.4 Horizontal seismic response at dam crest with exponential non-viscous damping model

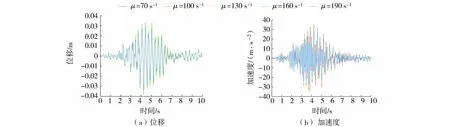
图5 坝顶水平向地震响应(高斯型非黏滞阻尼) Fig.5 Horizontal seismic response at dam crest with Gaussian non-viscous damping model

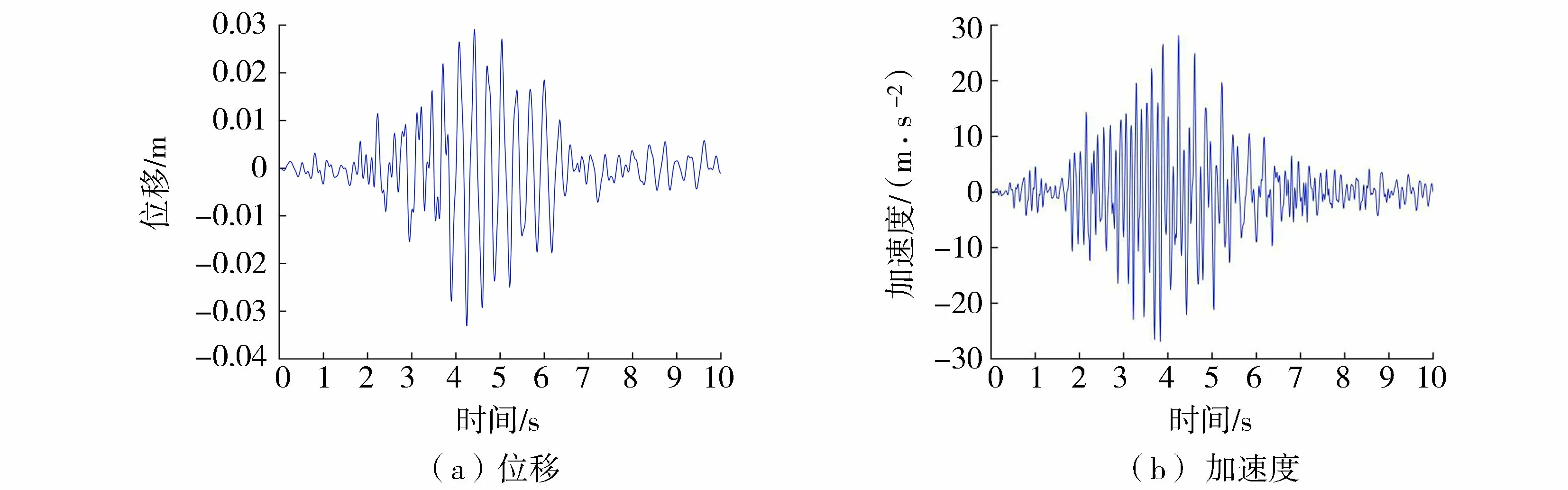
图6 坝顶水平向地震响应(黏滞阻尼模型)Fig.6 Horizontal seismic response at dam crest with viscous damping model

表1则分别给出了Δt为0.01 s、0.005 s、0.002 5 s情况下，计算得到的坝体水平位移、速度和加速度的响应峰值。

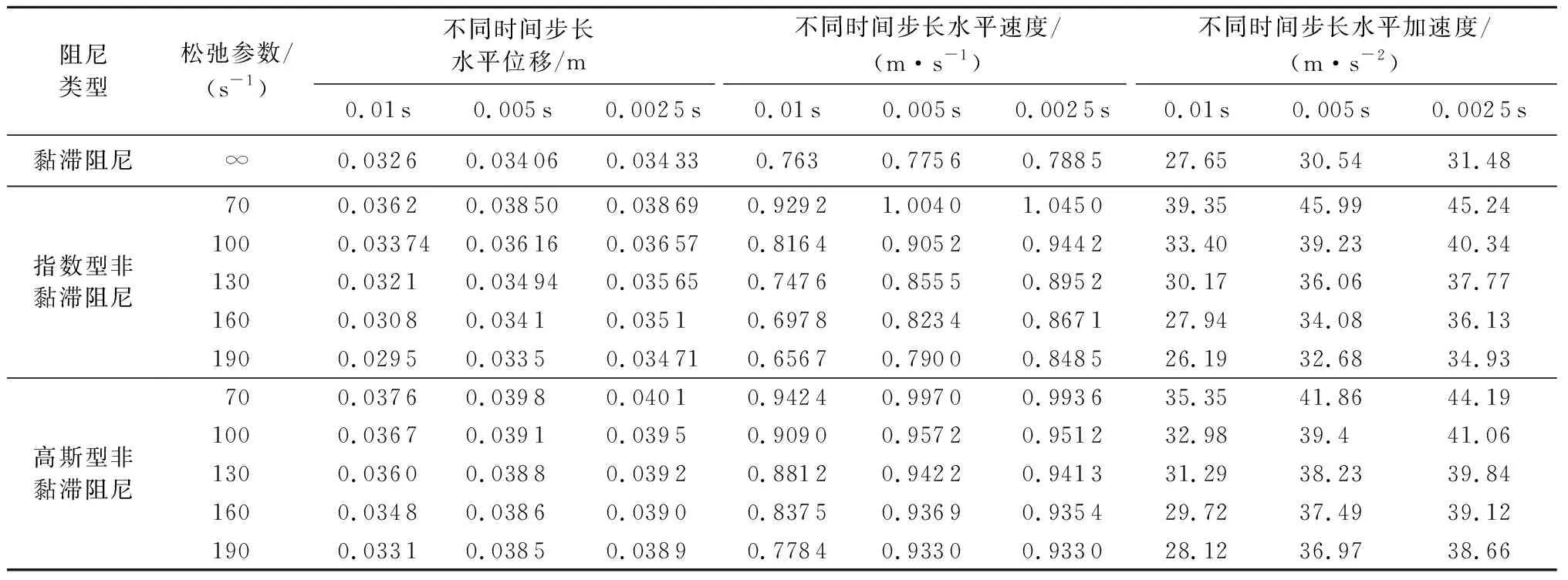
表1 坝体地震响应峰值

3.5 结果分析

从图4～6可以看出，各阻尼模型情况下，坝顶响应的时间变化规律基本一致，表明阻尼模型及松弛参数μ的变化对坝顶水平位移、加速度响应的时间变化规律影响不大。从图4和图5可以看出，虽然松弛参数μ的变化不影响响应的时间变化规律，但对响应的峰值有影响，无论是坝顶位移还是加速度，随着松弛参数μ的不断增大，响应的峰值不断减小，松弛参数越大，响应峰值越接近黏滞阻尼的响应峰值，与前面关于广义阻尼模型的理论分析相符。

由表1可以看出：①各阻尼模型情况下，随着直接积分时间步长的减小，响应峰值不断增大，说明Newmark直接积分法存在算法阻尼，以保证算法的无条件稳定性。因此，为了保证计算结果的精度，在条件允许的情况下，工程分析应尽可能采用较小的时间步长。另外，对于非黏滞阻尼模型，从表1中响应峰值随松弛参数μ的变化也可以看出，μ的数值越大，响应峰值越接近黏滞阻尼的响应峰值。②位移、速度和加速度响应峰值对阻尼模型、松弛参数和时间积分步长的敏感性不同，加速度响应峰值的敏感性最大，其次是速度响应峰值，位移响应峰值的敏感性最小，符合函数及其导数的变化规律。③比较高斯型非黏滞阻尼的结果，松弛参数μ从70 s-1变化至190 s-1，3种时间步长下的响应峰值始终大于黏滞阻尼的响应峰值，呈现从右侧一致逼近黏滞阻尼结果的趋势。当时间步长Δt≥0.005 s时，指数型非黏滞阻尼模型的响应峰值并不随着松弛参数μ的增大从右侧一致逼近黏滞阻尼结果的趋势，不符合核函数一致收敛于δ函数的趋势。当Δt=0.002 5 s时，指数型非黏滞阻尼模型的响应峰值才表现出随μ的增大从右侧一致逼近黏滞阻尼结果的趋势。由此说明，当采用Newmark直接积分法时，指数型非黏滞阻尼模型对时间步长的要求高于高斯型非黏滞阻尼模型。

4 结 语

本文根据黏弹性材料的广义流变模型导出了广义阻尼结构动力学方程，指出了经典的黏滞阻尼模型可以从Voigt-Kelvin本构模型导出，是广义阻尼模型的一种特例。以Koyna混凝土重力坝为例，进行了基于广义阻尼模型的地震响应分析。分析时分别采用指数核函数和高斯核函数2种广义阻尼模型，并与黏滞阻尼模型的结果进行了比较，表明地震作用下广义阻尼模型的响应峰值均大于黏滞阻尼模型的响应峰值。因此，有必要采用非黏滞阻尼模型进行混凝土大坝的地震响应分析。采用的Newmark直接积分法对卷积核函数的类型没有限制，是一种通用的时域求解方法，与状态空间法只适用于指数核函数相比，更便于嵌入现有的结构动力分析系统中。从本文算例的结果来看，指数型非黏滞阻尼模型对数值积分时间步长的要求高于高斯型非黏滞阻尼模型。本文对卷积积分采用了梯形积分格式，没有讨论其他积分格式对计算精度和耗时的影响，存在进一步改进和优化的空间。非黏滞阻尼模型中松弛参数μ的取值对计算结果有较大的影响，为了更加科学合理地分析混凝土结构的动力响应，应进一步开展相关试验和动力参数识别的研究，以确定混凝土材料的松弛参数。