粗粒料颗粒破碎三维离散元模型及其在密度桶试验中的应用

徐 靖，叶华洋，朱 晟

(1.河海大学水文水资源与水利水电工程科学国家重点实验室，江苏 南京 210098；2.河海大学水工结构研究所，江苏 南京 210098 )

粗粒料作为一种常用的筑坝材料，其最大粒径达600～800 mm，难以直接进行室内大型相对密度试验，为利用相对密度指标控制堆石坝的压实质量带来了极大的困难[1]。为了避免尺寸效应带来的影响，2002年田堪良等[2]提出了通过现场碾压试验来确定砂砾料最大、最小干密度的密度桶试验方法。2016年，朱晟等[3-4]在长河坝施工坝面首次开展了堆石料的现场密度桶试验，得到了不同分区的相对密度指标，并测得堆石料的Marsal破碎率小于10%。近年来，在阿尔塔什等高坝砂砾料的压实质量已经采用相对密度控制[5-6]，长河坝[3]、阿尔塔什[6-7]、两河口[8]等水利工程相继进行了堆石料的现场相对密度试验，并在阿尔塔什坝顶增模区得到成功应用。

然而，由于粗粒料现场大型相对密度试验的影响因素较多，导致其结果存在一定离散性，如车维斌等[9]依托两河口水利工程进行原级配堆石料的现场大型相对密度试验，测得最大干密度试验值低于现场原位碾压试验的结果。

粗粒料是典型的颗粒摩擦材料，破碎是其固有属性。颗粒破碎会导致土体级配改变，体积收缩，成为影响面板堆石坝应力、变形的决定性因素[10]。颗粒破碎问题十分复杂，众多学者采用室内试验、数值模拟和理论分析等手段进行了广泛研究。刘汉龙等[11]开展了室内大型三轴试验，研究了围压和峰值内摩擦角与颗粒破碎之间的关系；朱晟等[12]研究了级配和围压等因素对堆石料颗粒破碎的影响；徐琨等[13]从宏、细观尺度开展了颗粒破碎对堆石料填充特性缩尺效应的影响研究。颗粒流离散元方法作为一种能够有效模拟粗粒料力学特性的方法，在岩土工程众多领域得到广泛应用。

本文针对现阶段大型相对密度试验精度及影响因素等问题，基于三维颗粒流程序，建立可模拟粗粒料颗粒破碎的离散元模型，从装样级配偏差和密度桶尺寸效应等方面探讨引起密度桶法试验结果差异的原因，以期为两河口水利工程应用提供参考。

1 颗粒破碎离散元模型

目前，离散元法模拟颗粒破碎主要有黏结法(bonded-particle method，BPM)[14]和替代法(fragment replacement method，FRM)[15]。黏结法能够模拟不同形状单颗粒的破碎，但是难以考虑多次破碎及进行大规模颗粒集合体破碎的数值模拟研究，因此本文采用替代法进行颗粒破碎模拟，而替代法的关键在于母颗粒破碎准则的选取和子颗粒数目及空间分布的确定。

1.1 破碎准则

无黏性土和碎石的压实主要靠颗粒重排列和颗粒破碎来完成，颗粒破碎的发生是由于压实过程中颗粒局部受荷超过极限强度产生裂纹，裂纹扩展延伸进而导致颗粒接触点局部破碎。因此考虑颗粒的局部应力集中，采用Russell等[16]提出的最大接触力破碎判定准则，并考虑破碎强度的尺寸效应：

(1)

式中：d、d0分别为颗粒粒径和特征粒径，d0取1 mm；m为Weibull 模量；σlim,0为特征粒径材料的极限强度；AF为接触力作用域面积。对于任一颗粒，当其承受的最大接触力Fmax大于极限作用力时，颗粒破碎。

1.2 子颗粒组织模式

在数值模拟中，Borkovec等[17]采用Apollonian填充法来填充球体。Apollonian填充法要求母颗粒内的子颗粒间两两外切，母颗粒内切于部分子颗粒，且子颗粒间无重叠。对于三维母颗粒球体，初始子颗粒数为4个，然后逐级填充上级母颗粒，直至球体间的空隙被更小的球体填满，最终可以得到该颗粒破碎时的级配分形维数2.47[18]。

然而，实际的破碎过程是整体破裂、局部破碎、颗粒磨损三者共同作用的结果。孔宪京等[19]在试验前对20～60 mm粒径的12个颗粒进行了染色，发现试验后颗粒破碎部分多为颗粒的棱角，即局部破碎占主导。在堆石料振动压实过程中，颗粒的破碎多是由不规则棱角的磨损或边缘薄片的剥落造成的，较少发生颗粒的整体破碎。图1为现场相对密度试验试样压实后断面及代表颗粒破碎的裂纹的发展。以往使用替代法模拟颗粒破碎，达到破碎强度极限的母颗粒多是采用同一种子颗粒排列组合方式，即所有颗粒都发生整体破碎，这会过高估计颗粒破碎的影响。

图1 现场相对密度试验试样Fig.1 Sample for field relative density test

张科芬等[20]构建了4种考虑整体破碎的分级填充组织模式，研究了破碎自组织对级配演化以及材料宏、细观力学特性等的影响。笔者在此基础上进行了改进，建立另外4种组织模式，并将最大接触力方向向量与其相结合。首先获取母颗粒承受的最大接触力的方向向量，然后假定母颗粒中存在一个截平面，将最大接触力方向向量与截平面重合确定截平面方程；随后将最大子颗粒与母颗粒球面和截平面都相切以确定最大子颗粒的空间位置及半径；最后将剩余子颗粒按照Apollonian填充法逐级填充以达到模拟颗粒局部破碎的效果。图2为考虑整体破碎和局部破碎的4种组织模式，分别包含4、9、21和45个子颗粒。

图2 4种分级填充的组织模式Fig.2 Four organizational patterns of hierarchical filling

上述4种分级填充的组织模式，子颗粒并不能完全填充母颗粒。为保证颗粒破碎前后质量、体积守恒，在破碎阶段采用子颗粒膨胀法，为避免膨胀产生的局部应力过大，编译fish函数使得子颗粒在局部时间步长内低速膨胀。

1.3 模型建立

根据SL 237—1999《土工试验规程》室内相对密度试验的要求，数值模型中制样选取径径比为5(密度桶桶径与最大粒径的比值)，为充分振动压实，高径比暂定为3(密度桶高度与最大粒径的比值)。模型的级配根据堆石料的真实级配按相似级配法缩尺到最大粒径为60 mm确定，试验不考虑颗粒形状的影响，使用球体基本单元代替堆石料。

由于粒径越小，颗粒数越多，考虑到台式计算机的模拟计算效率，为了控制初始试样中颗粒的数目，最小初始颗粒粒径dmin取10 mm，粒径小于10 mm的颗粒按相同质量全部等效为10 mm颗粒，同时设定一个能发生破碎的最小颗粒粒径dlim=0.25dmin，其中dlim为破碎极限粒径。

细观参数参考文献[13，20]选择合适的初值，并利用两河口水利工程堆石料的室内三轴试验结果进行标定，反复试算最终确定对应的颗粒参数和颗粒破碎准则参数如下。①颗粒参数：颗粒密度ρs=2 650 kg/m3，材料摩擦系数μ=0.5，颗粒剪切模量G=3 GPa，颗粒的泊松比ν=0.3，dlim=2.5 mm。②颗粒破碎准则参数：直径为1 mm的颗粒特征强度σ0=800 MPa，d0=1 mm，m=10。③振动参数：振动器的静压力W=14 000 Pa，振动器最大激荡力Pmax=5 396 N，振动频率f=47.5 Hz。其中颗粒间的相互作用采用Hertz-Mindlin接触模型来描述。在三轴试验的模拟中，数值模型、物理试验的宏观应力-应变和体积变形规律如图3所示。由图3可以看出，离散元模型与物理试验的宏观应力-应变特征基本一致，体积变形特征略有差异，这是因为实际堆石料颗粒形状复杂多样且颗粒破碎的影响因素众多，而所建立的模型颗粒形状为圆球，破碎模式进行了一定的简化处理。

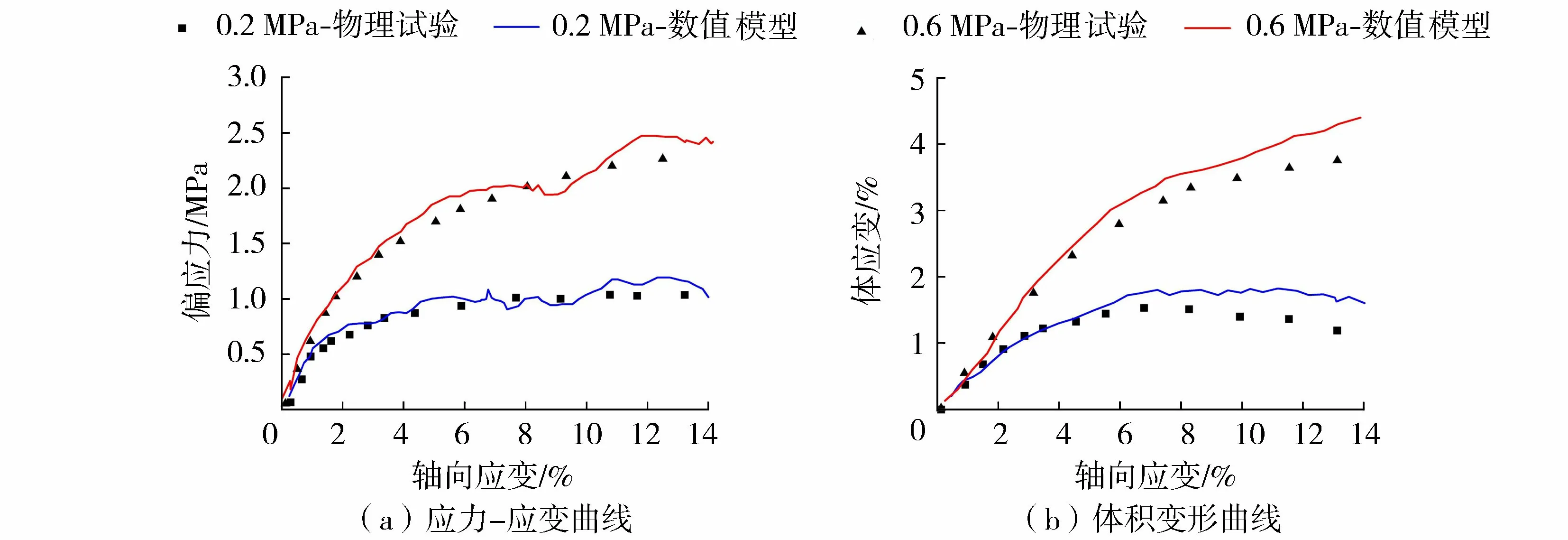
图3 两河口水利工程堆石料三轴试验结果模拟Fig.3 Simulation of triaxial test results of rockfill materials in Lianghekou water conservancy project

在室内堆石料压实过程中，试样受到表面振动器的主动力f(t)主要包括振动器自重I和Pmax，采用李杨等[21]现场碾压荷载等效模拟方法，考虑到室内振动器的实际压实工作特性，即一个周期内当振动器离开试样表面时视为未对试样产生作用力，因此任意t时刻振动器对试样的主动力P(t)(以竖直向下为正)为

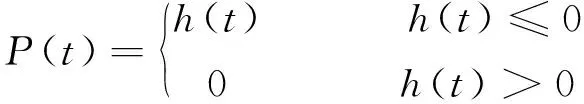
(2)

其中h(t)=I+Pmaxsin(2πft)

在数值模型中模拟振动荷载，首先生成圆柱型的clump实体，并使用fish函数(clump.force.app.y)施加如图4所示的主动力，以实现对振动器荷载的等效模拟。振动参数参考SL 237—1999《土工试验规程》取值。

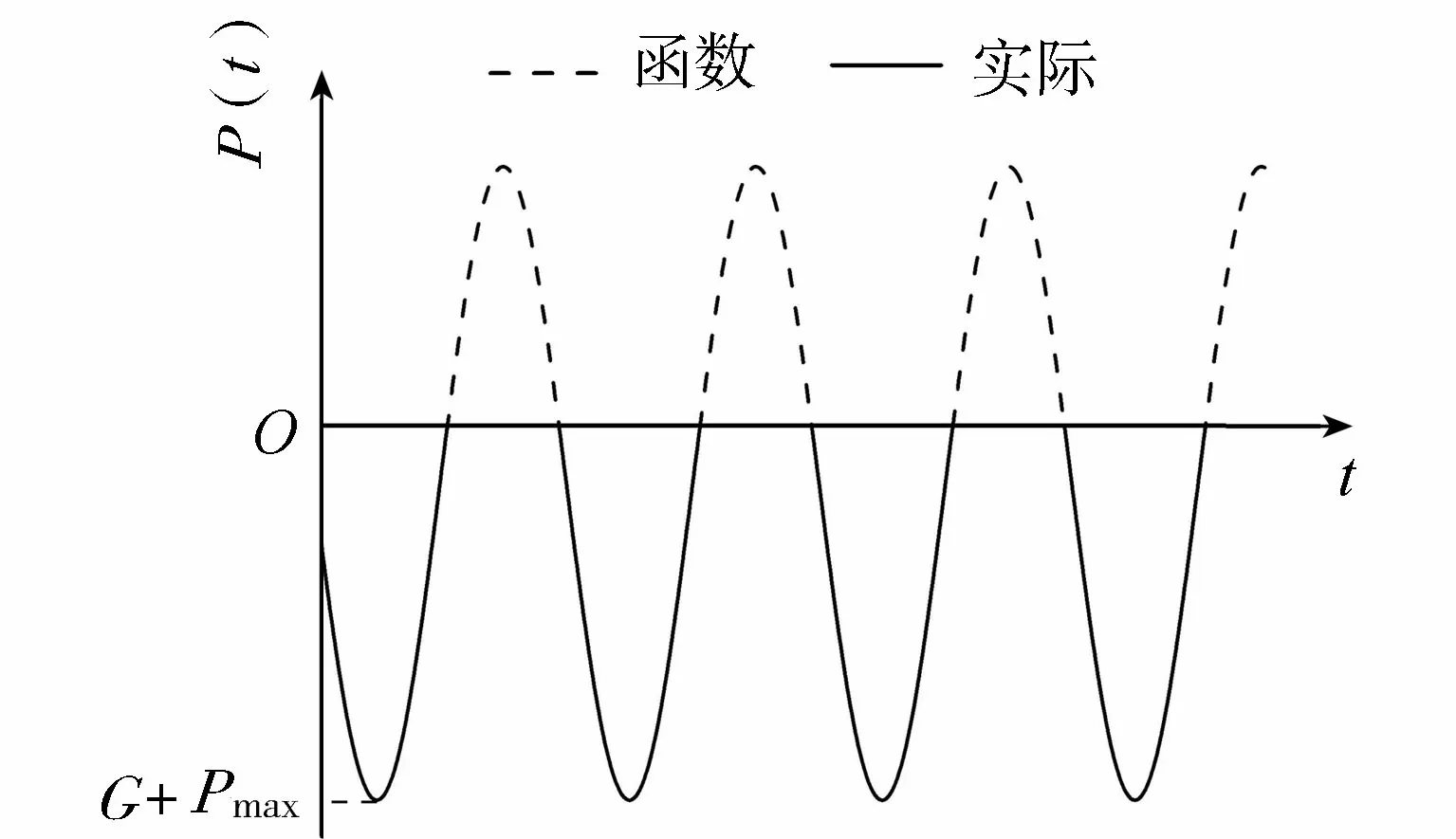
图4 主动力随时间变化规律示意图 Fig.4 Change law of vibrator main force with time

在圆柱形区域内通过粒径膨胀法生成初始孔隙率为0.45的级配试样，待颗粒在自重作用下下落达到自然稳定状态后使用clump技术在试样表面上方生成振动加载板，直到加载板和试样充分接触并稳定后得到初始试样。启动振动子程序，并每隔一定的时间步长启动破碎判别子程序。考虑到膨胀阶段和振动阶段互不影响，当颗粒膨胀时，破碎判别和振动子程序均不启动，待由膨胀产生的局部应力和不平衡力消散后再启动。最终，建立的计算模型如图5所示，模型中的颗粒总量为9 856，蓝色颗粒表示未发生破碎的球体，紫色颗粒表示处于一次破碎状态的球体，颗粒颜色越丰富表示试样越易发生多次破碎。

图5 堆石料相对密度试验的离散元模型Fig.5 Discrete element model of rockfill relative density test

1.4 不同组织模式的差异

重点分析整体破碎和局部破碎方式下堆石体振动压实前后宏、细观力学性质的差异性，综合考虑选取二级填充组织模式(即9颗粒模型)，并选定两河口水利工程设计下包线级配建立初始模型。

以数值模拟标定直径1 mm的颗粒强度800 MPa表示实际两河口水利工程砂板岩同粒径颗粒强度，选取合适的梯度，设定3组特征强度分别为1 000 MPa、800MPa、600MPa。为方便演示，整体组织编号为“-T”，局部组织编号为“-L”。图6为单对数坐标系下的级配曲线，可以看出当特征强度分别取1 000 MPa、800 MPa时，两种破碎方式的振后级配曲线差异性不大；当特征强度取600 MPa时，母颗粒更易发生破碎，破碎总量大，由此级配曲线的差异性显现出来，此时整体破碎组织模式相较于局部破碎组织模式的破碎量更大。

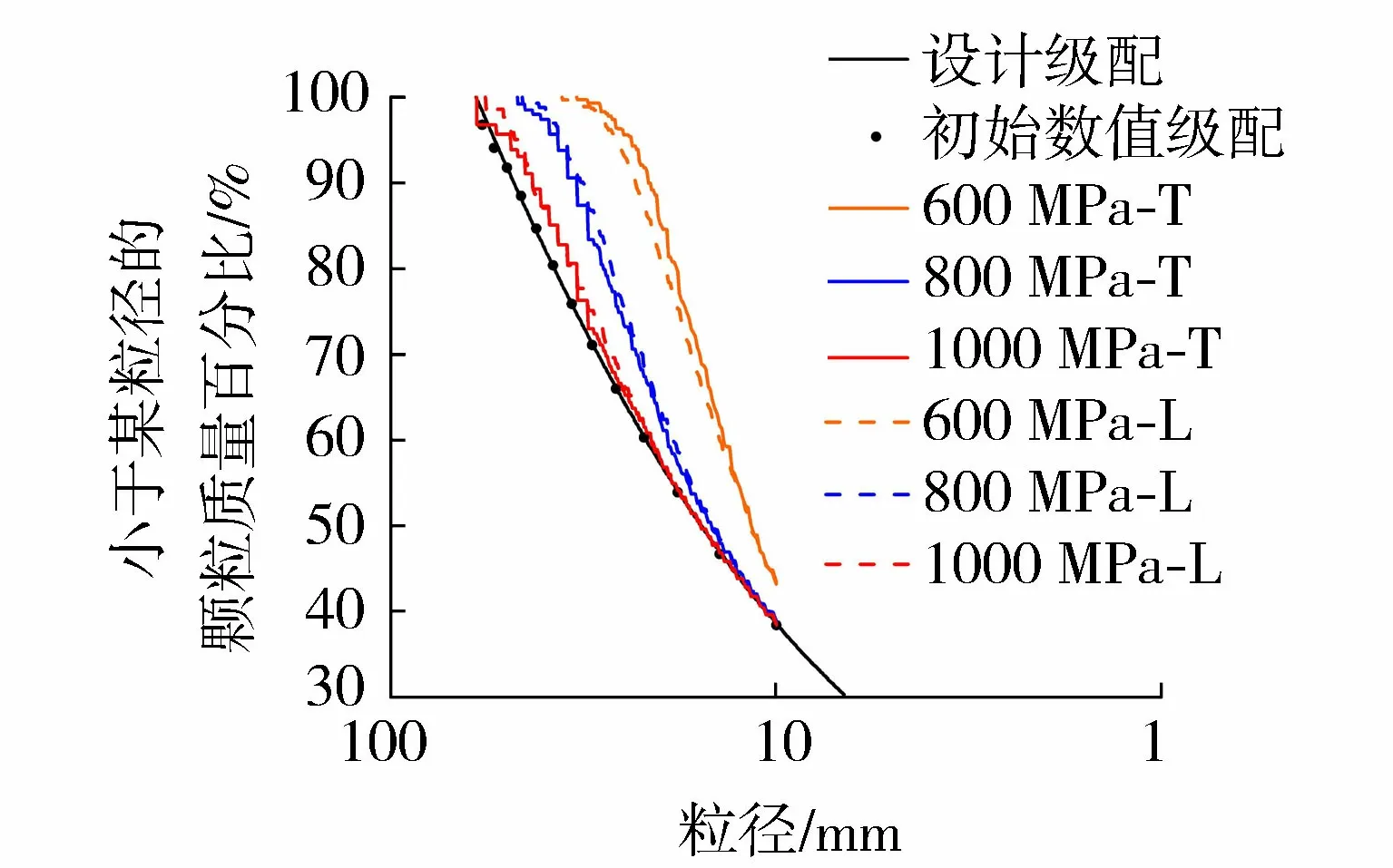
图6 不同组织模式的级配曲线Fig.6 Gradation curves of different organization patterns

图7为不同特征强度下各级破碎状态的颗粒质量及数目百分比。由图7可以直观看出，随着特征强度的降低，两种组织模式未破碎颗粒的质量及数目百分比都在减少，即特征强度越小越易破碎，且随着破碎级数的增大，处于各级的颗粒质量及数目百分比都迅速减小；两者区别在于不同的特征强度下，局部破碎组织模式的破碎级数更多，表明局部组织方式更易发生多次破碎。下面从力链差异和力学配位数差异分析其内在机理。

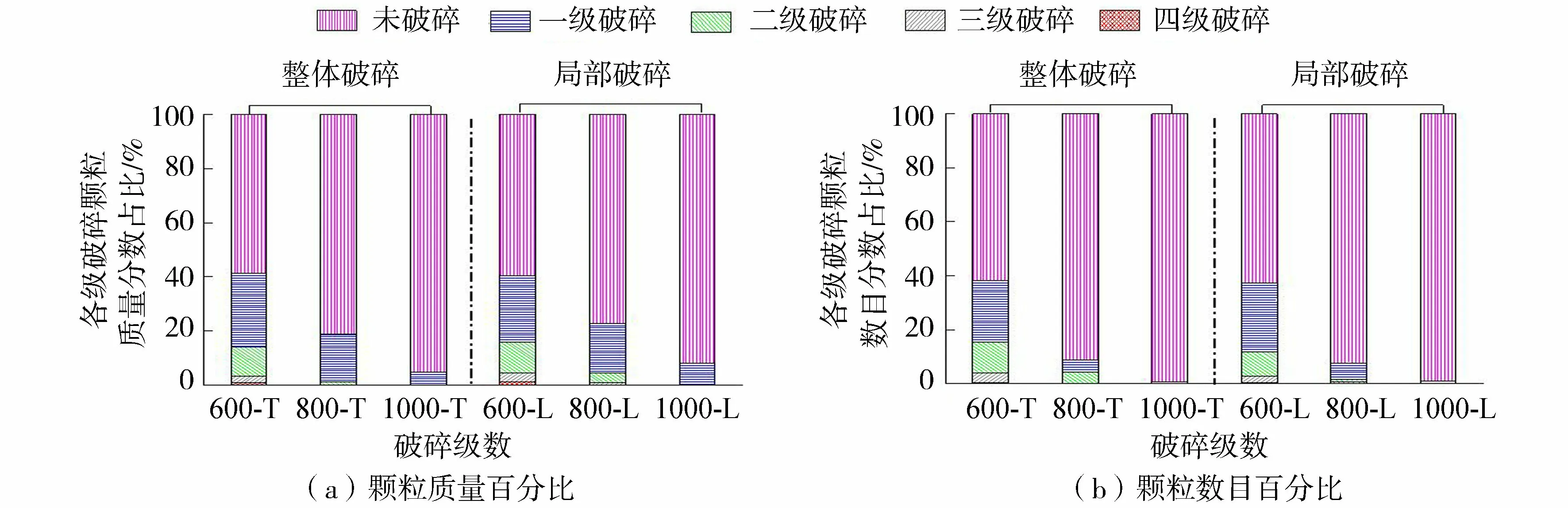
图7 颗粒破碎各级状态统计Fig.7 State statistics of particle crushing at different levels

1.4.1 力学配位数对比

Thornton[22]指出，颗粒周围有1个或0个接触对试样的力学稳定性不构成影响。基于该思想，首先定义力学配位数Nm：

(3)

式中：Cb为试样中颗粒间的接触总数；Cf为颗粒与墙体的接触总数；Nt、N1、N0分别为试样中颗粒总数、配位数为 1 的颗粒数和配位数为0的颗粒数。

采用力学配位数的频率分布去反映堆石块体破碎前后集合体的填充特性。由图8可知，不同组织模式的配位数频率分布曲线相似，但数值上存在较为明显的差异。初始试样、整体破碎和局部破碎的试样中，力学配位数为3的颗粒的频率均是最大值。配位数取2时初始试样的频率最大，可认为初始试样为松散堆积结构，经过振动后不同的破碎组织模式配位数为2的频率都很低，说明不同试样都趋向于密实结构。配位数取3、4、5时整体破碎组织模式的频率更大，这是因为小颗粒周围的接触数相对于大颗粒更少，整体破碎产生了更多的粒径偏小的颗粒。破碎后小颗粒增多，一方面颗粒间接触力相对减小，另一方面小颗粒强度较大，颗粒较难达到破碎应力，相应地破碎级数越大的颗粒数越少。配位数取5以上局部破碎组织模式频率更大，可认为破碎后仍然保留粒径相对较大的颗粒。由于大颗粒强度低，相应的局部破碎更易发生多次破碎。

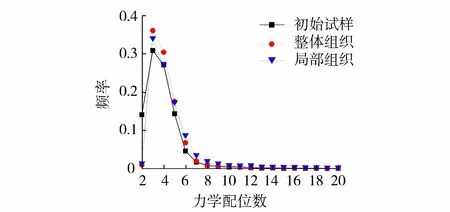
图8 力学配位数频率分布 Fig.8 Frequency distribution of mechanical coordination number

1.4.2 力链对比

借助Liu等[23]提出的破碎前后接触力概率密度函数去度量颗粒间的力链分布。接触力的概率密度定义为接触力出现在某一范围的概率，最小区间范围取5N。图9为截取了不同组织模式接触力概率密度差异最大的区间。由图9可知，试样在破碎过程中采用整体破碎组织模式的接触力在10～20 N时其概率密度比初始试样和局部破碎组织模式试样更大，即整体破碎组织模式对承力结构的影响更大，造成力链结构趋向于均匀化，在一定程度上夸大了颗粒破碎的程度。因此本文采用局部破碎组织模式(更符合颗粒的典型破碎模式，如图1所示)来探究两河口水利工程现场相对密度试验方法合理性问题。

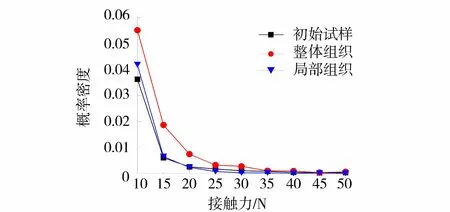
图9 接触力概率密度函数Fig.9 Probability density function of contact force

2 模型密度桶试验中的应用

为探讨相对密度试验结果精度的影响因素，结合两河口水利工程堆石料的密度桶试验资料[9]，主要从设计级配和试验装样的差异、密度桶尺寸效应两方面进行分析。

2.1 级配偏差和颗粒强度的影响

选取有较为明显差异的两河口水利工程板岩设计下包线和试验装样级配作为本次数值模拟的对象，并按照相似级配法进行缩尺得到最大粒径为60 mm的级配曲线，如图10所示。

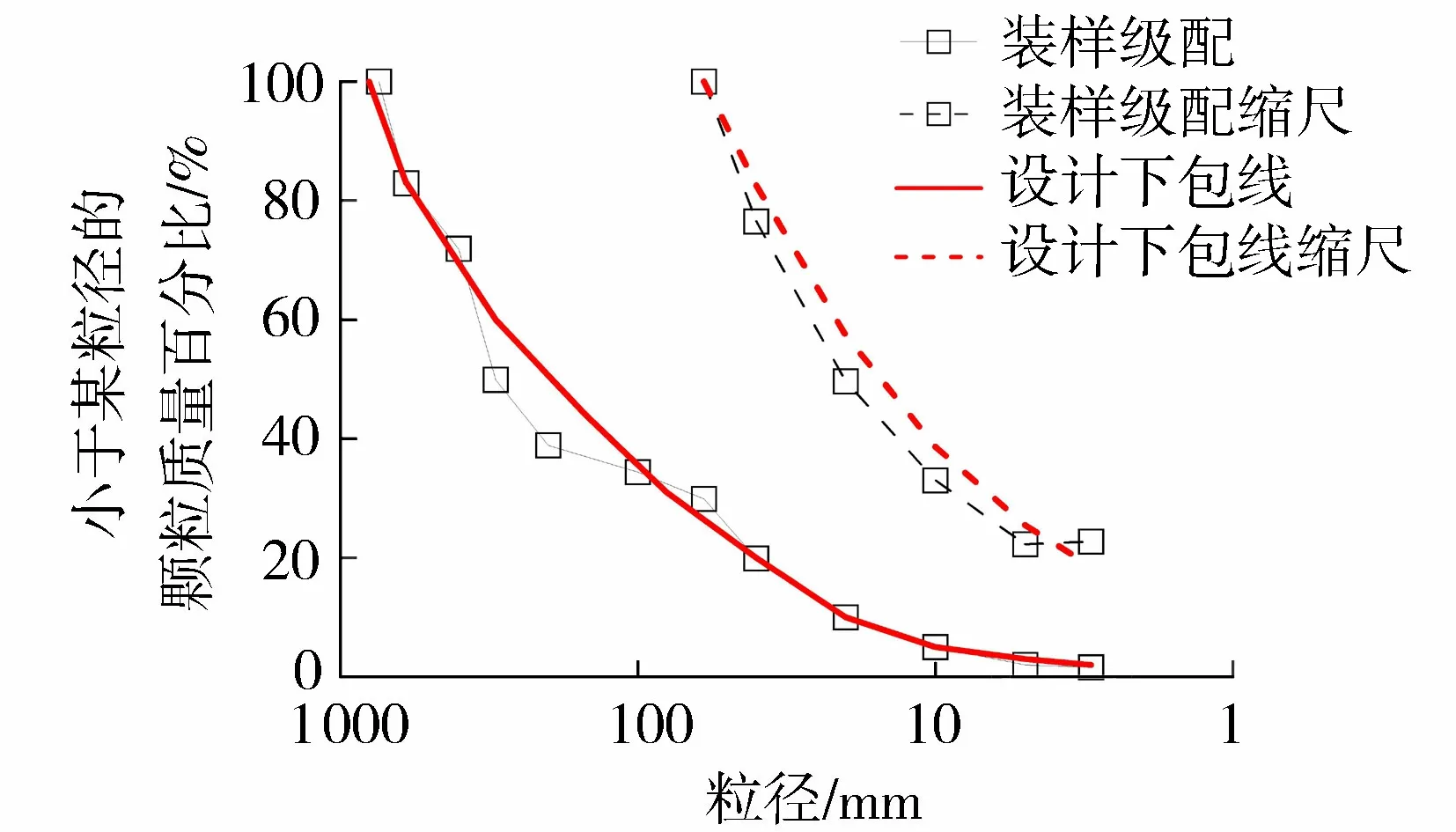
图10 设计级配和试验装样级配Fig.10 Design gradation and test sample gradation

采用Hardin[24]提出的相对破碎率Br指标定量描述颗粒破碎的多少。Br的定义是：将颗粒级配曲线与0.074 mm 粒径竖线所围成的面积定义为破碎势Bp，Bp代表颗粒的破碎潜力。颗粒破碎前后Bp的差值为破碎量Bt，则Br为Bt与破碎前Bp的比值。该方法认为颗粒破碎的极限粒径为 0.074 mm，小于该粒径的颗粒不再破碎。

图11为设计包线和试验装样级配在不同的特征强度下，振动相同时间后孔隙率和破碎率的差异性,其相同之处在于颗粒的特征强度越小，Br越大，振后孔隙率e越小，即极值干密度越大。

图11 孔隙率及破碎率与特征强度的关系 Fig.11 Relationship between porosity, crushing rate and characteristic strength

特征强度取1 000 MPa时，设计包线和试验装样级配的e分别为0.336、0.314，Br分别为0.091、0.102，即破碎率相差不大，而孔隙率相差较大；特征强度取600 MPa时设计包线和试验装样级配的e分别为0.285、0.281，Br分别为0.378、0.435，特征强度越小，破碎率的差异显著增大，而孔隙率的差异减小。即试样越不易破碎，级配偏差对相对密度试验中试样孔隙率的影响越大，可认为级配偏差使得颗粒的空间分布排列出现更大的差异性，改变了颗粒的充填结构。试样越易破碎，孔隙率的差异性减小，说明颗粒破碎在一定程度上能弱化级配偏差对试样孔隙率的影响。

由图12可见，初始的设计包线和试验装样级配接触力概率密度有一定的差异性，即级配的变化改变了颗粒之间的堆积形态，导致颗粒之间的接触关系及传力性态发生了改变。振动压实后接触力概率密度差异性减小，即试样都趋向于更加稳定的结构，设计包线和装样级配接触力分布的差异，主要体现在较小接触力的概率密度不同。

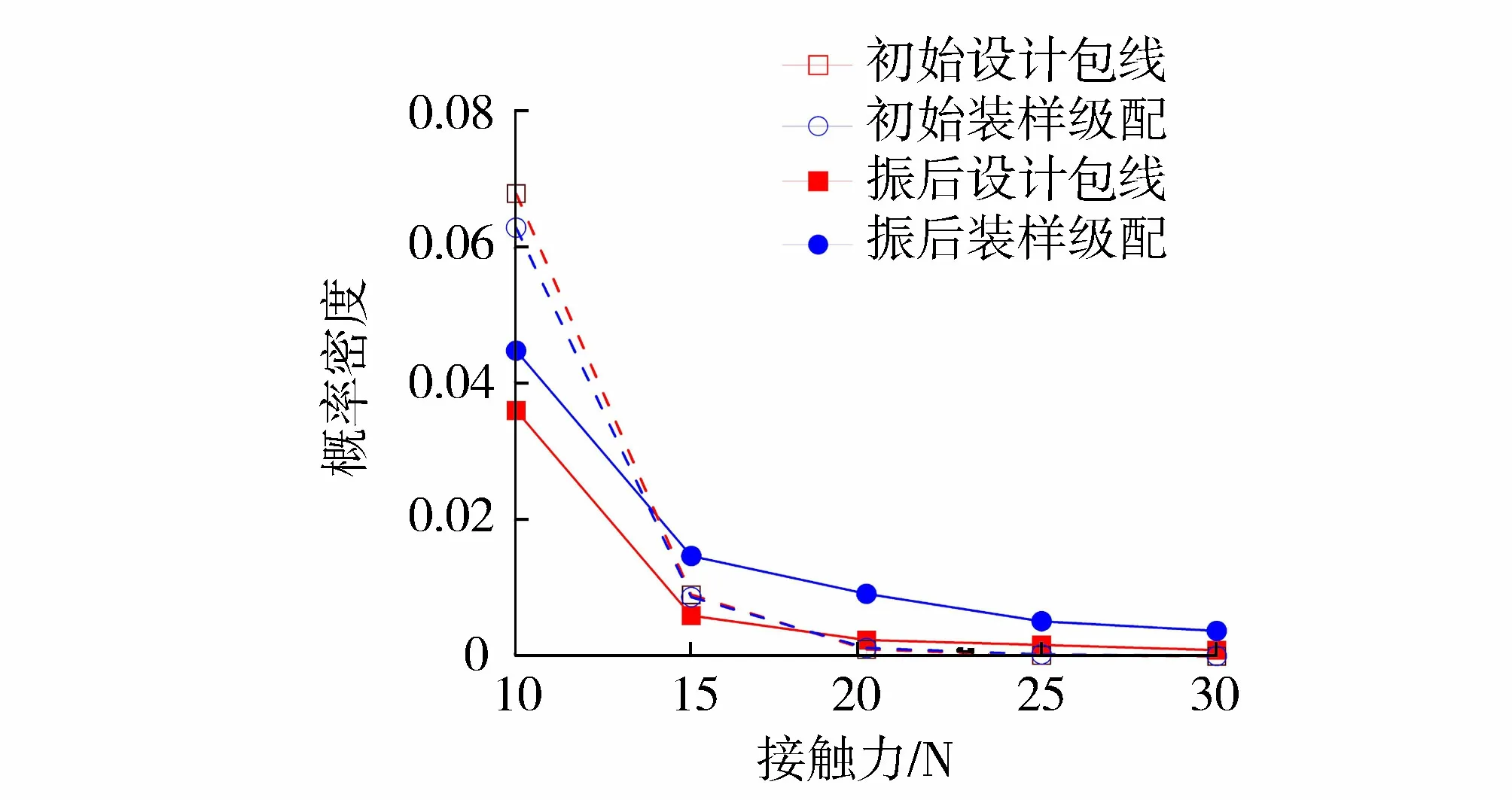
图12 不同级配的接触力概率密度函数Fig.12 Probability density functions of contact force with different gradation

2.2 密度桶尺寸效应影响

控制密度桶内径一致，以分析不同高径比密度桶试验的宏、细观力学响应。图13为不同高径比的试样振动压实后的模型图，图中蓝色代表原始未发生破碎的颗粒，灰色是蓝色颗粒发生1级破碎后的颗粒，橙色是灰色颗粒发生2级破碎后的颗粒，黄色是橙色颗粒发生3级破碎后的颗粒，紫色是黄色颗粒发生4级破碎后的颗粒。由图13可以直观地看出不同的高径比试样中破碎颗粒数目占总数目的百分含量、破碎到各级颗粒的数目分布情况、破碎颗粒的空间分布状态等都有一定的差异。高径比取1时破碎颗粒数目百分含量更大，试样表面破碎量更多；而高径比取5时破碎颗粒百分含量和表面破碎量都相对较少。

图13 不同高径比数值模拟试样Fig.13 Numerical samples with different height-diameter ratios

图14为孔隙率、力学配位数及破碎率与高径比的关系。由图14可见，随着高径比增加，孔隙率减小，力学配位数增加；高径比为1的试样的孔隙率与高径比为2、3、4、5的试样相比明显偏大，力学配位数明显偏小。高径比越大，相对破碎率越小。

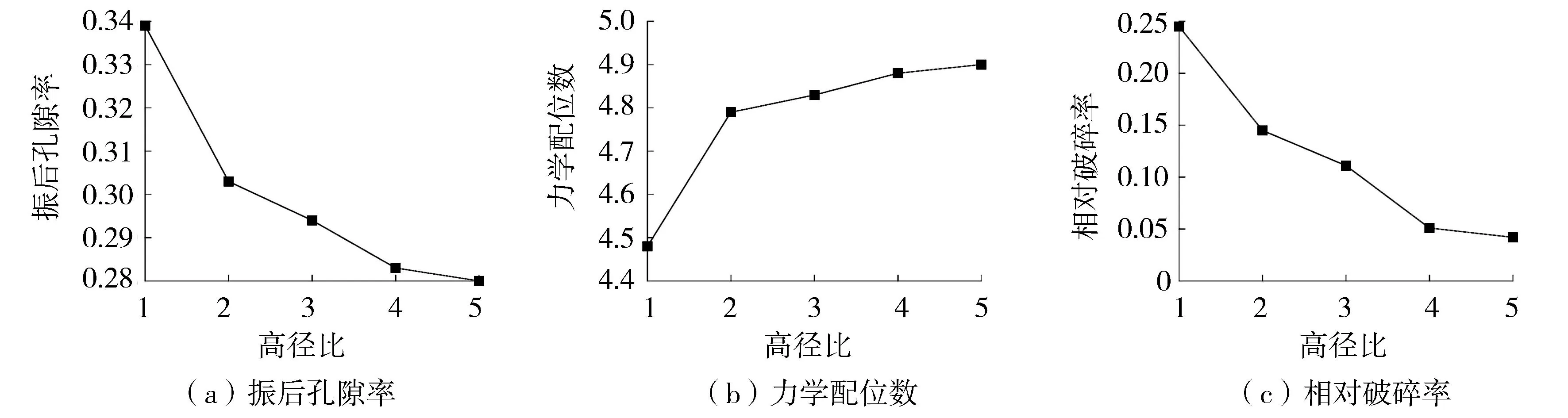
图14 高径比与宏细观力学参数关系Fig.14 Relationship between the ratio of height to diameter and the macroscopic and meso-mechanical parameters

试样的密实程度是颗粒间重排列和颗粒破碎两者共同作用的结果，因此，高径比是影响相对密度试验结果的重要因素之一。高径比过小时，由于大颗粒的顶托作用，其力学配位数较小，造成颗粒间接触力过大，导致了更大的破碎率；同时大颗粒之间的架空作用不利于不同粒径颗粒位置的调整，使得试样无法充分密实。这也是密度桶试验中高径比较小时最大干密度试验值甚至低于现场碾压试验检测结果的原因，以该试验值代表级配的最大干密度作为现场压实检测标准时，会出现相对密度大于1 的情况。此时适当增加高径比更有利于颗粒位置的调整和填充，但过大的高径比会造成用料量过大的问题，且现场堆石碾压过程的应力沿层深呈指数衰减[25]，底层堆石料亦不能充分压实，因此根据数值模拟结果，现场相对密度试验的高径比至少应大于2.0，并根据现场实际的振动碾参数、用料量对其进行相应的调整，从而获得真正意义上的最大干密度，才能符合相对密度的使用条件。

3 结 论

a.本文基于阿波罗填充建立的考虑整体破碎和局部破碎的三维离散元模型为粗粒料颗粒破碎模拟提供了一种思路。整体破碎和局部破碎差异可从宏观级配演化、细观力学配位数、力链结构等方式进行反映。

b.颗粒特征强度越高，级配偏差对于极值干密度试验值的影响越大。不同工程的母岩性质不同，对结果的影响程度亦有差异，在进行相对密度试验时，要严格控制试验装样级配，使其尽可能不要偏离目标级配。

c.在进行大型相对密度试验时需要考虑密度桶尺寸与颗粒粒径之间的关系，高径比不宜过小，以免大颗粒的顶托作用而导致不能真正压实，高径比应大于2.0，并根据现场实际进行合理的调整。