基于三维极限分析法的GIM和SRM边坡安全系数计算结果对比

洪 勇，邵珠山，石广斌，聂兴信

(1.西安建筑科技大学资源工程学院，陕西 西安 710055；2.西安建筑科技大学土木工程学院，陕西 西安 710055； 3.西安建筑科技大学理学院，陕西 西安 710055)

自然界以及工程边坡更多的具有三维空间特性，运用三维稳定性分析方法研究边坡稳定性更符合实际情况。目前三维边坡稳定性分析方法主要有极限平衡法、数值分析法和极限分析法[1]。极限平衡法是三维边坡稳定性分析中使用最为广泛的方法，但大多数研究和应用是从二维平面向三维空间的拓展和修正，使用中需对静力平衡和滑动面等做出许多假定，导致二维极限平衡法固有的一些缺陷和弊端在三维分析中依然没有得到解决，有些不足甚至得到放大，对三维边坡稳定性分析结果的准确性产生了一定的影响。随着计算机技术和数值方法的发展，三维数值方法能够准确直观地反映边坡三维几何形状、边界条件、应力应变关系等信息，模拟边坡破坏渐进过程，越来越广泛地应用于三维边坡稳定性分析，但工程人员熟练掌握还存在一定的困难，此外，分析和研究过程中存在边坡破坏临界标准不统一以及数值计算结果与试验和现场结果存在差异等问题，在实际工程中应用较少。极限分析法具有严密的理论基础，且求解过程简便。2009年，Michalowski等[2]提出了一种三维边坡牛角转动破坏模型，基于该牛角转动破坏模型，相关学者开展了大量的采用极限分析法的三维边坡稳定性的相关研究。

目前常用的计算边坡安全系数FS的方法有强度折减法(strength reduction method，SRM)和容重增加法(gravity increase method，GIM)[3]。这两种方法在运用有限元法计算FS中研究较多。Zhang等[4-7]认为SRM和GIM定义安全系数方式不同，使用范围也略有不同。GIM定义简单明确，计算表达式为显性；SRM由于其为隐式表达式需迭代计算，但在有限元计算中基于已有程序实施简单而被普遍使用。Michalowski等[2]在其首次提出的三维牛角破坏模型极限分析上限理论中采用SRM计算FS，并从理论上分析了结果为最优上限解时，对比其他研究结果仅是特定边坡参数下的特定值。

基于三维边坡牛角转动破坏模型，国内外众多学者研究了不同破坏模式(坡趾破坏、坡面破坏、坡底破坏)[8]、边坡几何形态[9]、考虑土体非均质性和各向异性[10]、边坡裂缝[11]、加固形式[12]、孔隙水压力[13]、地震荷载[3]、岩质边坡稳定性分析[14]等复杂情况下边坡三维极限分析，拓展了边坡三维极限分析的应用范围，与其他研究结果比较表明，基于三维边坡牛角转动破坏模型的极限分析法可以用于边坡稳定性分析，但是计算FS时，主要基于SRM。Wang等[13]基于极限分析法，提出了一种分层总和法计算边坡重力功率和内能耗散，并结合极限分析理论和GIM的特点，在其相关研究中均采用GIM法计算FS；Yang等[3]分析探讨了SRM和GIM在不同参数下的敏感性规律，并总结得出两者经验关系：SRM计算FS值为GIM的2/3次方；Saada等[14]采用GIM计算岩石FS，结果表明采用GIM与传统的最大剪应力与滑面剪应力之比定义安全系数具有等效性。

由以上分析可知，SRM和GIM相关研究更多见于有限元法计算FS的研究中，而随着极限分析法的快速发展和广泛应用，两种方法在极限分析法中计算FS还需深入研究。鉴于此，本文建立了考虑坡顶倾角的三维边坡牛角转动破坏模型，基于极限分析理论构建功率平衡方程，利用满足约束条件的穷举法优化求解FS最小值，在考虑参数c/γH、内摩擦角φ、坡顶倾角α以及边坡倾角β的情况下，定量对比分析了SRM和GIM计算的边坡安全系数，可为边坡工程稳定性分析、设计与施工提供参考。

1 三维边坡牛角转动破坏模型

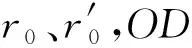
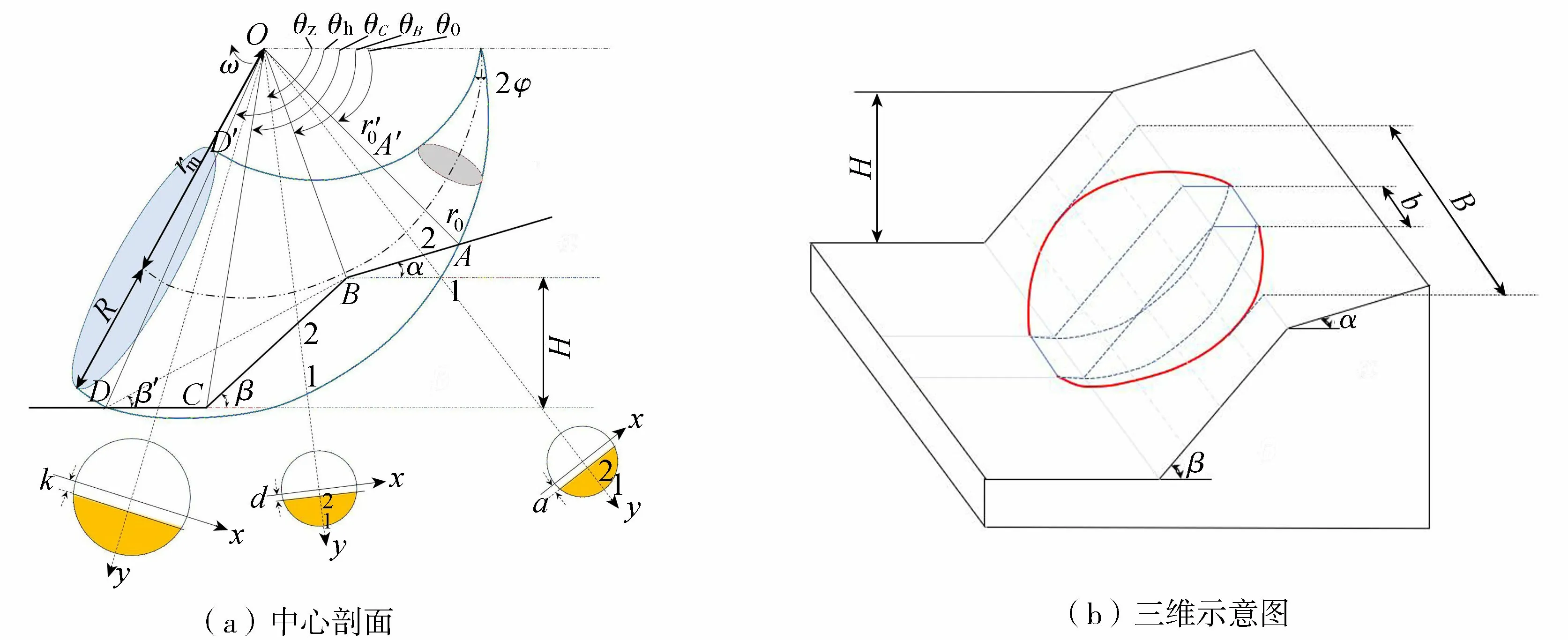
图1 三维边坡牛角转动破坏模型Fig.1 Horn-like rotational failure model of three-dimensional slope

r=r0e(θ-θ0)tanφ

(1)

(2)

图1(a)中，过O轴任意平面与三维牛角相交所得剖面均为圆形，剖得所有圆心的连线为三维牛角状圆锥面的中心轴线rm，如图1(a)中虚线所示，可以表示为

(3)

过O轴所作平面与三维牛角状曲面相交所得剖面圆半径R可以表示为

(4)

对于宽度很大的边坡，考虑模拟破坏的实际状态，在三维边坡牛角转动破坏模型对称面处插入宽度为b的块体，如图1(b)所示，随着b的逐渐增大，插入段在组合破坏模型中逐渐占据主导地位，当b→+∞时，边坡三维稳定性问题可以简化为平面应变问题。

2 边坡三维稳定性极限分析

极限分析上限理论可以表述为：在一个假设的运动许可速度场中，在满足速度边界条件和应变与速度相容条件下，外力所做功率小于或等于内部耗散功率。本文三维边坡牛角转动破坏模型的能耗计算包括重力产生功率和滑面内能耗散。计算中，分别计算边坡的三维牛角状破坏部分和中间插入段能耗，然后统一建立三维边坡牛角转动破坏模型下的功能平衡方程。

2.1 外功率

边坡外功率是由边坡材料重力产生的功率。按照坡面形态，滑动体由θ0-θB、θB-θC、θC-θh三部分组成，由这三部分产生的重力功率Wγ-3D计算表达式为

(5)

a、d和k分别为三维边坡牛角转动破坏模型中心轴线至坡顶AB、坡面BC和坡底CD的最短距离，可表达为

(6)

(7)

(8)

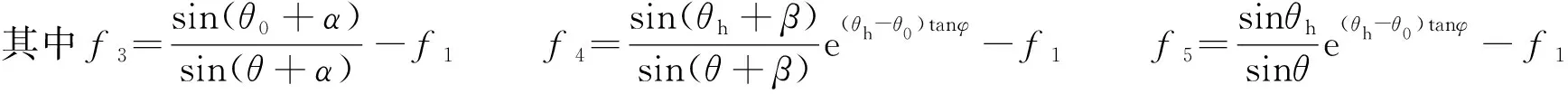
OB和OC对应的转角θB、θC由三角函数关系计算可得：

(9)

(10)

(11)

式中L为AB段长度。

对重力功率计算式进行解析积分可得：

(12)

平面插入段重力功率的计算与二维破坏模型类似，只需再乘以平面插入端的宽度b即可：

(13)

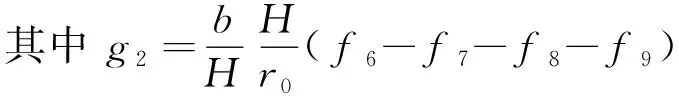
外功率总和为

W=Wγ-3D+Wγ-insert

(14)

2.2 内能耗散率

破坏模型的内能耗散率也由θ0-θB、θB-θC、θC-θh三部分组成，可以计算得到不含插入块体的三维边坡牛角转动破坏模型的内能耗散率为

(15)

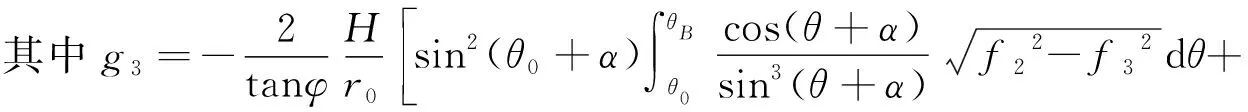
平面插入段的内能耗散率也可以分为三部分，平面插入段的内能耗散率为

(16)

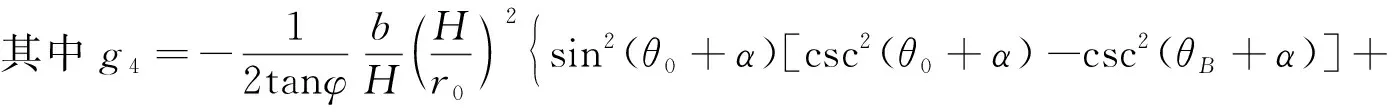
因此，破坏模型总的内能耗散率为

DV=DV-3D+DV-insert

(17)

2.3 边坡三维安全系数求解

根据虚功率原理，令整个三维牛角转动破坏模型外功率与内能耗散率相等，有：

Wγ-3D+Wγ-insert=DV-3D+DV-insert

(18)

将式(14)(17)代入公式(18)并化简可得：

(19)

3 安全系数求解

3.1 GIM

根据GIM的定义，FS为增加后的外力与初始外力之比，即

FS=kcr/k=qcr/q

(20)

式中：k、q分别为土体初始重力和荷载；kcr、qcr分别为增加后的重力和荷载。根据功率计算公式，功率与外力呈线性关系，因此，FS等于临界外力功率Wcr除以实际外力功率W，即：

Wcr=WFS

(21)

基于极限分析上限理论，当内能耗散率等于增加外力所做功率时，三维边坡处于极限平衡状态，此时：

D=Wcr

(22)

联合式(21)(22)可得：

FS=D/W

(23)

由式(23)可知，FS定义为内能耗散率与外力做功功率之比，即

(24)

3.2 SRM

SRM基本原理是将土体强度参数(c、φ)同时除以折减系数F，将该组新参数作为土体强度参数进行计算，直至边坡达到临界破坏状态，此时的F为边坡安全系数FS，计算过程为

cm=c/F

(25)

tanφm=tanφ/F

(26)

将式(25)(26)代入式(24)可知：

(27)

式(27)是FS的隐函数。

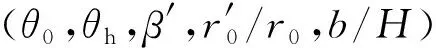
3.3 最小安全系数

基于上述分析，将式(24)(27)转化为求解：

minFS=FS(θ0,θh,β′,r0′/r0,b/H)

(28)

约束条件为

(29)

式中：b′为三维边坡牛角转动破坏模型的牛角部分最大宽度；B为边坡总宽度。

3.4 对比验证

自然状态下的边坡验证，是对一般黏性土三维边坡进行临界高度及安全系数验证。众所周知，当具有临界高度的三维边坡处于极限状态时，其安全系数等于1.0。Taylor[15]最早定义无量纲参数γH/c为边坡稳定性系数NS，现有相关研究沿用该定义方式[2]，NS能反映边坡的安全状态。基于文献[2，8-9]中γH/c值，分别采用SRM和GIM计算FS，以验证本文方法及程序的正确性，验证结果如表1所示。

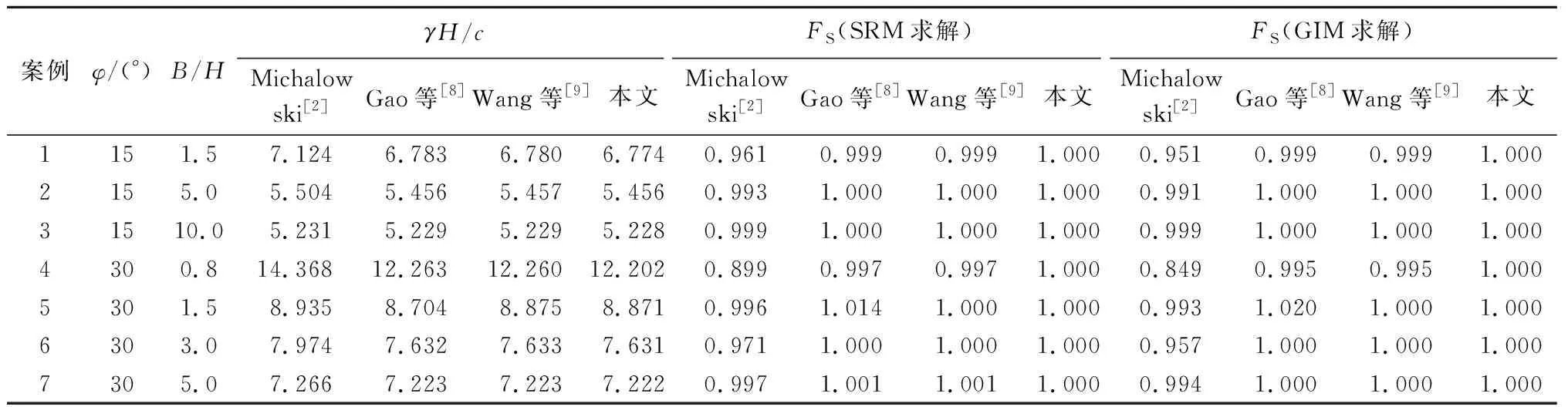
表1 本文研究与现有研究结果对比

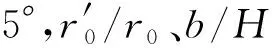
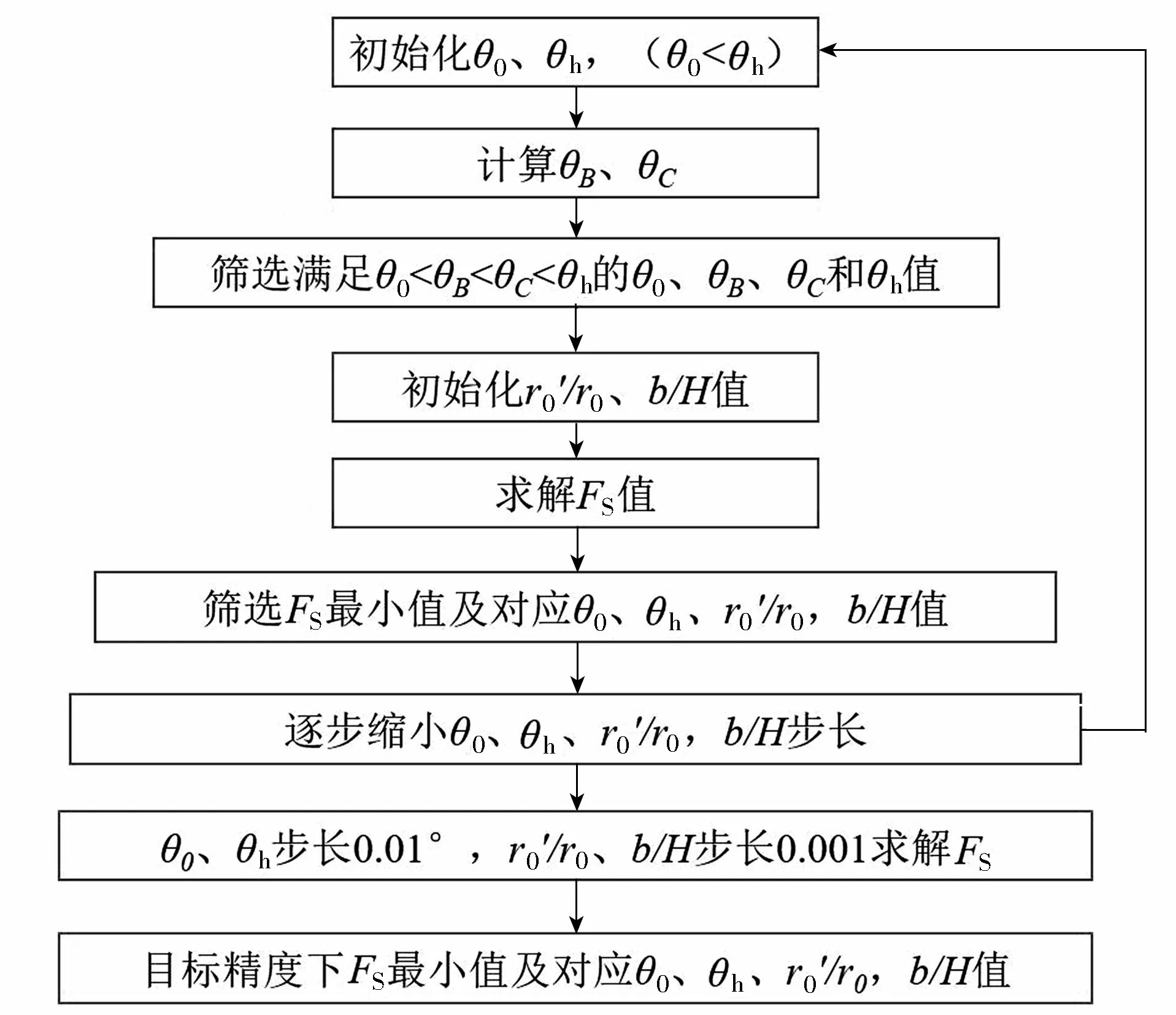
图2 边坡安全系数优化求解流程Fig.2 Optimization solving process of slope safety factor

4 边坡三维效应及参数分析

4.1 边坡案例

为分析两种方法计算FS结果的不同，以某一均质边坡进行参数分析，该边坡主要参数为：φ=15°，β=60°，在参数c/γH=0.116以及B/H=1.0时，相关学者对其进行了研究。计算结果表明该边坡二维情形下FS为1.0，其中基于极限分析法的上限法和下限法计算结果分别为1.02和0.98[16]，二维分析时各方法一致性较好；三维分析时，本文计算结果分别为1.484(GIM)和1.325(SRM)，而卢坤林[16]、Hungr等[17]、Leshchinski等[18]、Hovlan[19]计算结果分别为1.26、1.23、1.25和1.189，Huang等[20]等基于简化和严格的三维极限平衡法计算结果分别为1.204和1.243，Li[21]等基于上限法和下限法计算结果分别为1.44和1.27。

对比已有研究，本文采用GIM和SRM两种方法求解FS结果与上限法计算结果接近，而相比其他学者计算结果均偏大。与上限法计算结果接近原因为研究理论相同，都基于极限分析法上限理论。相比于其他文献，本文计算结果偏大的原因是三维牛角转动破坏模型计算边坡安全系数时，假定边坡滑体形态为两端牛角状三维锥体+中间平面插入段，与文献[16]中圆柱+锥体形态滑体类似，计算规律与文献[16]规律一致。对于二维均质边坡，Leshchinsky等[18]采用变分法严格证明了对数螺旋线(牛角转动破坏模型上下边界线)破坏模型是边坡极限平衡闭合解对应的最危险破坏机制，且与极限分析法上限解等效，但是拓展至三维空间，对数螺旋破坏模型是否为均质边坡最危险破坏机制还需进一步研究。但无论采用哪一种破坏模型，只要与边坡最危险破坏机制接近，该破坏模型下边坡相关参数就能定量反映边坡稳定性影响规律，即滑体形态不影响边坡参数对边坡稳定性的规律。

4.2 边坡三维效应分析

上述算例中，边坡二维和三维安全系数计算结果相差较大，且三维相比二维计算结果偏大。以上限法为例，三维比二维计算结果大41.17%，表明边坡具有明显的空间效应。对具有明显空间效应的边坡进行稳定性分析时，二维计算结果偏保守，按二维计算结果对边坡进行治理加固，其设计相对更安全，但一定程度上会带来较大的经济和工程浪费，反之，反演边坡安全强度参数时会过高估计，使边坡安全稳定性评估和设计偏于不安全而产生隐患，因此边坡稳定性分析时需考虑边坡空间效应(宽高比B/H)的影响。为了研究不同B/H值时边坡的三维稳定性，分别选取边坡不同B/H值，并采用GIM和SRM求解边FS，如图3所示。

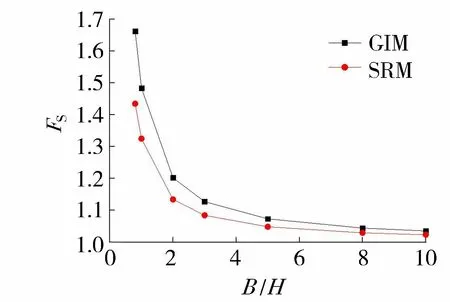
图3 不同宽高比下边坡安全系数Fig.3 Safety factors of slope under different width to height ratio

由图3可知，B/H对FS影响显著，具体表现为：B/H<3时，边坡三维效应显著，随着B/H增加，FS急剧降低；B/H>3时，FS随B/H增加而降低，但降低趋势较缓，最终趋于1.0。从采用的计算方法分析，SRM所计算FS值小于GIM。随着B/H减小，GIM所计算FS值远远大于SRM，而随着B/H增加直至趋于二维分析时，两种方法所计算FS值逐渐接近直至趋近1.0时相等。从FS具体数值分析，当B/H=5时，GIM和SRM计算结果分别为1.073和1.048，相比二维平面计算结果分别大7.3%和4.8%，三维计算结果与二维计算结果相差分别在10%和5%以内，可知B/H=5时边坡稳定性分析三维结果和二维结果相差较少，尤其采用SRM分析时。此外，绝大多数边坡失稳案例其宽高比B/H<5[16]，基于此，以前述边坡案例B/H=5为例，分别采用GIM和SRM，研究不同参数c/γH、φ、α和β下FS变化规律。

4.3 参数分析与讨论

图4反映了不同参数c/γH、φ、α及β下采用GIM和SRM对FS的影响规律。由图4可知，随着c/γH和φ增大，FS提高，而随着α和β增大，FS降低。计算结果表明，当FS=1时，两种方法计算结果接近且近似都等于1；FS>1时，GIM计算结果大于SRM，且FS越高，GIM计算结果相对越大；FS<1时，SRM计算结果大于GIM，且FS越小，SRM计算结果相对越大。此外，FS>1表示边坡稳定，FS=1表示边坡处于极限平衡状态，FS<1表示边坡不稳定，与一般规律一致。

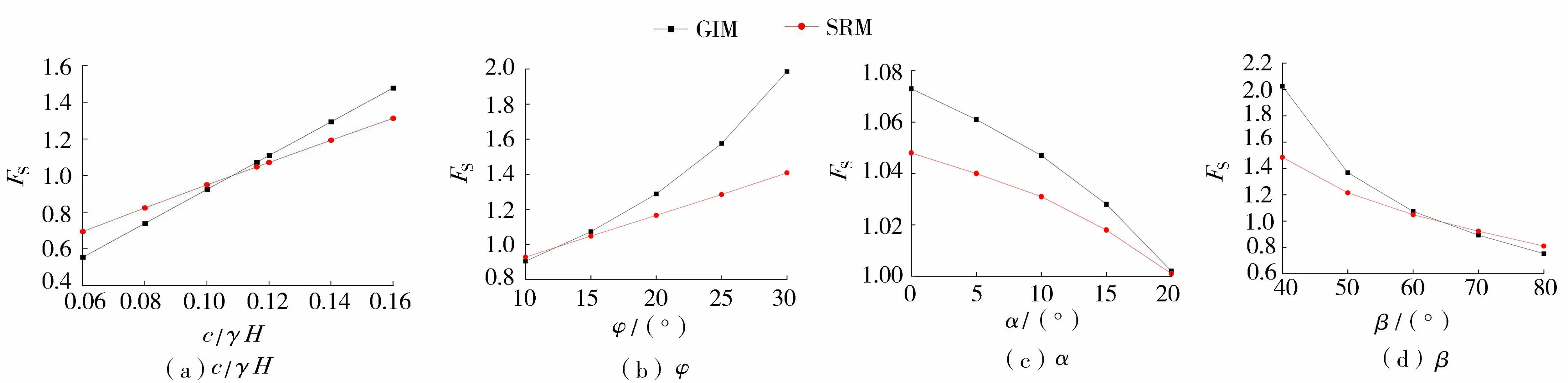
图4 不同边坡参数下边坡安全系数Fig.4 Safety factors of slope under different slope parameters

具体而言，c/γH与FS呈线性关系，即随着c/γH增大，FS线性提高。φ增大，FS增加，符合一般规律。当FS>1时，随着φ增大，GIM相比SRM计算结果呈显著增加，这与两种方法计算FS的原理一致。α增大时，FS减小，当α逐渐增加至等于边坡倾角时，边坡可视为二级边坡，符合随边坡倾角增加边坡安全系数降低的一般规律。β越大，FS越小，且随β增大呈显著降低趋势。

基于极限分析法分析边坡安全稳定性时，GIM和SRM计算FS存在差异，与两种方法的计算原理不同有关。使用GIM时，增加岩土材料容重在增加下滑力的同时，也增加了抗滑力，从而使得FS计算值偏大，对于强度参数较大的边坡尤甚，图4(b)GIM计算所得FS曲线呈抛物线形，明显反映了这一规律。使用SRM时，同时对边坡岩土黏聚力和内摩擦角进行折减，再代入岩土模型进行计算，计算所得FS相对较小，计算结果相对保守，但结果乐于被工程技术人员接受。

FS计算结果对工程设计影响较大，GB 50330—2013《建筑边坡工程技术规范》规定，对于一般工况下的永久边坡，等级为一级、二级和三级时对应安全系数分别为1.35、1.30和1.25，即相应等级和工况边坡的安全系数应不小于规范规定值，不满足时应对边坡进行处理。以此规范为例，采用GIM和SRM取FS<1.35进行分析，两种方法计算结果对比如图5所示。

图5 SRM与GIM边坡安全系数计算结果对比Fig.5 Result comparison of slope safety factor using SRM and GIM

由图5可知，GIM和SRM计算结果误差最大为10.46%，最小为0.09%，除最大误差外其余均在10%以内。FS<1.2时，两种方法计算结果误差均在5%以内，整体呈现边坡越稳定(FS越大)，计算误差越大；边坡越趋于极限状态(FS=1)，误差越小甚至计算结果相等。对于按规范需加固边坡，采用SRM计算FS结果偏保守，而GIM计算结果相对偏大，但误差均在5%以内，且边坡越趋于极限状态，两种方法计算FS结果误差越小甚至相等。对于稳定性好以及非常稳定的边坡计算FS时，除了考虑边坡荷载、几何形态以及岩土体参数等因素外，还需关注计算方法对边坡稳定性的影响。

5 结 论

a.基于极限分析理论所推导含坡顶倾角的边坡安全系数FS计算表达式，利用MATHEMATICA软件编写的优化计算程序计算边坡的安全系数，对比已有研究结果表明，本文推导公式及编写程序是正确有效的，且求解相对更优。

b.宽高比B/H越小，边坡三维效应越显著，反之，B/H越大，边坡二维特性越明显。B/H>5时，相比二维计算结果，GIM和SRM计算FS三维结果误差分别在10%和5%以内；B/H<5尤其当B/H<3时，边坡三维效应不容忽视，采用三维模型及参数计算更符合边坡工程实际情况。

c.安全系数FS随参数c/γH和内摩擦角φ的增大而提高，随坡顶倾角α和边坡倾角β的增大而降低。当FS=1时，GIM和SRM计算结果接近且近似都等于1；FS>1时，GIM计算结果大于SRM，且FS越大，GIM计算结果相对越大；FS<1时，SRM计算结果大于GIM，且FS越小，SRM计算结果相对越大。对于FS在1.2以下的稳定边坡，GIM和SRM计算结果误差在5%以内，边坡越接近极限稳定状态，两种方法计算结果误差越小。