TC4合金在不同表面强化状态下的微动磨损性能研究
刘柏,王宁,朱金龙,郝世奇,张显程
TC4合金在不同表面强化状态下的微动磨损性能研究
刘柏,王宁,朱金龙,郝世奇,张显程
(华东理工大学 承压系统与安全教育部重点实验室,上海 200237)
研究喷丸(SP)及表面超声滚压(USRP)强化后摩擦系数、残余应力场及塑性应变场对TC4合金微动磨损性能的影响。分别对TC4合金表面进行SP及USRP强化处理,通过试验测得强化前后的表面粗糙度、残余应力以及显微硬度。基于改进的Archard磨损方程,在ABAQUS有限元软件中建立微动磨损的二维柱面/平面接触模型,借助ABAQUS中的子程序SIGINI和HARDINI分别将残余应力场、塑性应变场引入到表征微动磨损的UMESHMOTION子程序中,从而探究表面强化后摩擦系数、残余应力场以及塑性应变场对平面微动磨损性能的影响。原试样经SP强化后,表面粗糙度增加,而经USRP强化后,表面粗糙度得以改善。经SP和USRP强化后,试样的显微硬度分别为原试样的1.28倍和1.23倍。TC4合金经USRP处理后,最大残余应力为–550 MPa,而SP处理后为–380 MPa。引入残余应力场后,试样的磨损深度明显减少,相比原试样,USRP、SP试样的磨损深度分别降低15%、10%。引入塑性应变场后,TC4合金的磨损深度降低了约6%。相同载荷条件下,摩擦系数越大,磨损越严重。磨损轮廓会随着摩擦系数的增大而逐渐往外侧偏移,接触中心区域的磨损深度也随着摩擦系数的增大而越来越深。塑性形变行为会随着摩擦系数的增加而变得明显,且最终会使得塑性变形的区域变得越来越大。引入残余应力场和塑性应变场后,磨损量均会减小,残余应力的影响更为显著。通过微动疲劳试验发现,加入微动磨损作用后,试样寿命显著降低,USRP试样的抗磨损性能最显著。
表面强化;微动磨损;残余应力场;塑性应变场;UMESHMOTION子程序
微动磨损是指两接触体之间由于变载荷或振动的作用,产生微米级的相对运动,从而引起材料损失的现象[1]。这种现象可能发生在许多工程实际中,例如轴承–轴、螺栓连接和铆钉联接、钢缆以及燃气轮机等[2-5]。微动磨损会使得接触区域的材料发生脱落,而材料的损失不可避免地会对其性能产生恶劣的影响。此外,微动磨损还极易促进裂纹的形成,从而降低构件的疲劳寿命,造成巨大的经济损失和安全隐患。
TC4合金因具有比强度高、高温性能稳定等一系列优点而成为航空航天领域应用广泛的材料之一,然而因其摩擦系数大,且耐磨性差,加之对微动磨损特别敏感,极易受到微动磨损的影响,从而大大降低其服役寿命[6]。表面强化作为提高材料表面性能的常用手段,可以很好地提高TC4合金的抗微动磨损性能。喷丸(SP)、表面超声滚压(USRP)等强化工艺可以使工件材料具有强韧性,同时还具有高硬度、高耐磨性和高疲劳强度。除此之外,还能引入较深的残余应力[7-9]。Liu等[10]对比研究了USRP对17-4PH钢的表面完整性、常规疲劳以及微动疲劳行为的影响规律,试验结果表明,USRP处理时间对17-4PH钢的普通疲劳和微动疲劳性能有显著影响。主要原因是USRP可以引入梯度纳米结构,较大的残余压应力和较高的显微硬度,这些因素都有助于提高17-4PH钢的普通疲劳和微动疲劳寿命。Ren等[11]研究了不同表面超声滚压工艺参数对高强度高韧性钛合金微动磨损性能的影响,试验表明,工艺参数中滚压次数为30遍、振动幅值为7时,抗磨损性能最佳。因为在该工艺下有较低的表面粗糙度、更高的显微硬度值和更深的残余应力层。Kumar等[12]在研究不同接触材料(SAE52100钢和氧化铝)对表面机械研磨处理后的TC4合金微动磨损行为的影响时发现,当接触材料为氧化铝时,经SMAT处理后的试样的磨损量最低,大约为原试样的1/4,这可以归因于较高的表面硬度、较低的切向力系数、纳米晶体表面层的存在以及SMAT处理过的样品中更多的TiO2层。
目前,关于微动磨损的研究主要包括试验[13-15]和有限元仿真2种方式。然而,通过试验方法来研究微动磨损不仅经济成本高,而且试验周期也相对较长,更重要的是,对于接触区域的应力应变分布和微动参数一般很难获取。通过有限元模拟可能很好地解决这些问题,随着有限元理论的发展,使得有限元分析成为微动磨损研究中不可或缺的一部分。Szolwinski等[16]首先将临界平面方法应用于微动损伤问题,该方法可在多个不同的平面上求得最大的疲劳损伤参数,并根据临界损伤平面来预测微动疲劳寿命。Tang等[17]建立了锆合金的二维平面/柱面接触模型,通过有限元数值模拟其微动磨损行为,发现部分滑移与整体滑移状态下的磨损性能存在差别。Tong等[18]探究了摩擦力的变化对微动磨损的影响,结果表明,当考虑部分滑移条件的磨合阶段时,摩擦系数发生变化的有限元模型获得的预测更接近于试验结果。李玲等[19]研究了循环次数、法向载荷以及位移幅值对柱面/平面微动磨损磨损深度及体积的影响,同时对部分滑移和完全滑移状态下的磨损结果进行了对比研究。张慧杰等[20]基于改进的Archard磨损方程,建立了二维柱面/平面微动磨损模型,从平面的磨损宽度和磨损深度分析了柱面半径、柱面材料弹性模量、泊松比3个参数对平面磨损轮廓的影响。Arnab等[21]借助有限元模型研究了摩擦系数、硬度和杨氏模量对微动磨损的影响,结果表明,磨损率受硬度和杨氏模量的影响显著,施加的摩擦系数对磨损率几乎没有影响。
基于上述的一系列研究发现,大多数的微动磨损仿真中,很少会将表面强化所引入的有益因素(摩擦系数、残余应力场以及塑性应变场)考虑到仿真模拟之中,这显然是不符合实际情况的。本文通过建立微动磨损的二维柱面/平面接触模型,对经SP以及USRP后TC4试样摩擦系数、残余应力场以及塑性应变场的变化对其微动磨损性能的影响进行有限元模拟探究。借助ABAQUS中的子程序SIGINI和HARDINI分别将残余应力场以及塑性应变场引入到表征微动磨损的UMESHMOTION子程序中,同时还考虑了在微动磨损过程中,接触区域发生塑性损伤时循环塑性的影响。本文还搭建了一套微动磨损装置,通过微动疲劳试验结果与模拟有限元结果相互验证。
文中SP、USRP以及原(AsR)试样的摩擦系数、残余应力场以及塑性应变场数据均通过表面粗糙度、残余应力以及显微硬度试验所得。其中,表面粗糙度由表证,并借助IFMG4表面三维形貌仪分别测量不同表面强化后试样的表面粗糙度,如图1所示。残余应力通过Proto-IXRD MG40P FS STD残余应力分析仪测定,测试试样为5 mm×5 mm×6 mm的长方体,选用Cu靶,X射线发生器管电压为24 kV,管电流为7 mA,准直管直径为1 mm,曝光时间为5 s。为了准确获得SP和USRP处理后沿深度方向的残余应力场,采用逐层电解法进行残余应力的测定。电解抛光液按高氯酸与甲醇体积比为1︰9进行配制,抛光电压为15 V。在测定残余应力时,需对每一深度的水平方向测试3个不同的位置,通过求平均值的方式来减小试验误差,残余应力分布如图2所示。显微硬度是通过HXD-1000MC/CD显微维氏硬度仪来进行测定,主要的设置参数有:施加载荷为1.96 N,保载时间为15 s。同一深度测量5个有效数据点取其均值,其中每个数据点间隔50 μm,同时沿深度方向间隔50 μm测量一次硬度值。此测量方法可以在获得足够数据点的同时,可以尽量减小硬度压痕对相邻数据点的影响,其分布如图3所示。
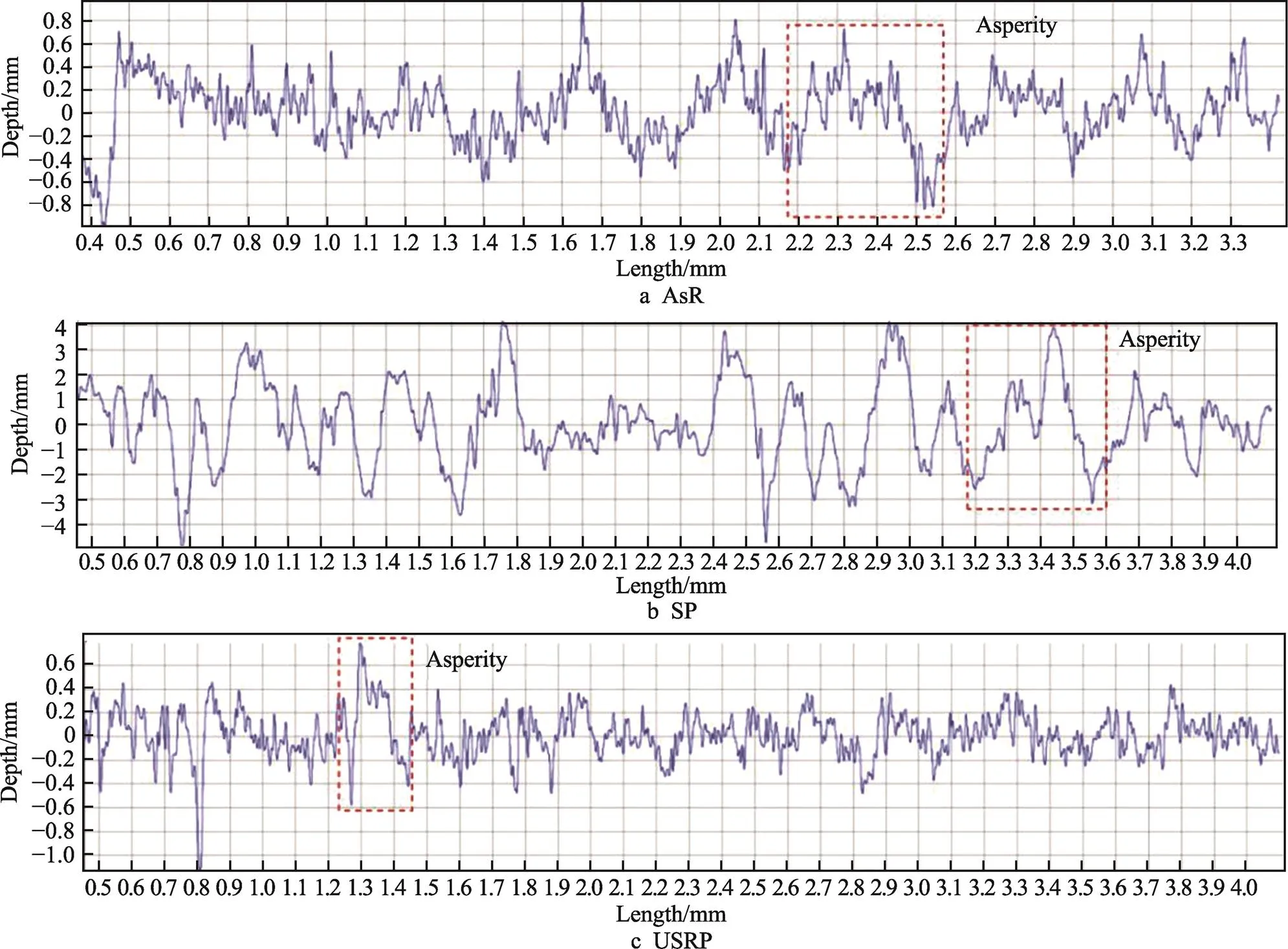
图1 不同表面处理后试样表面粗糙度
Fig.1 The surface roughness under different surface strengthening
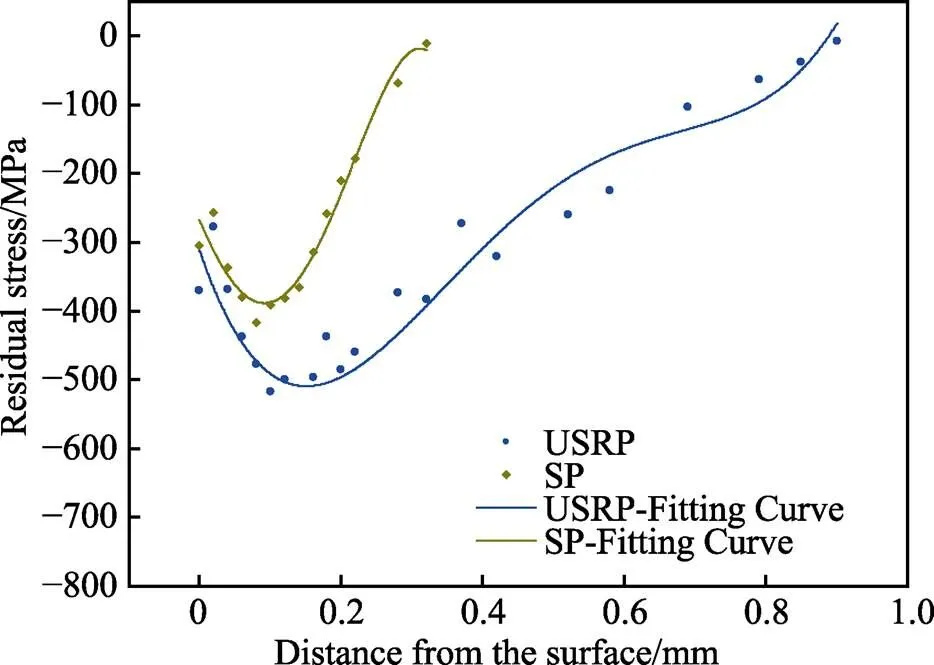
图2 不同表面处理后试样残余应力分布
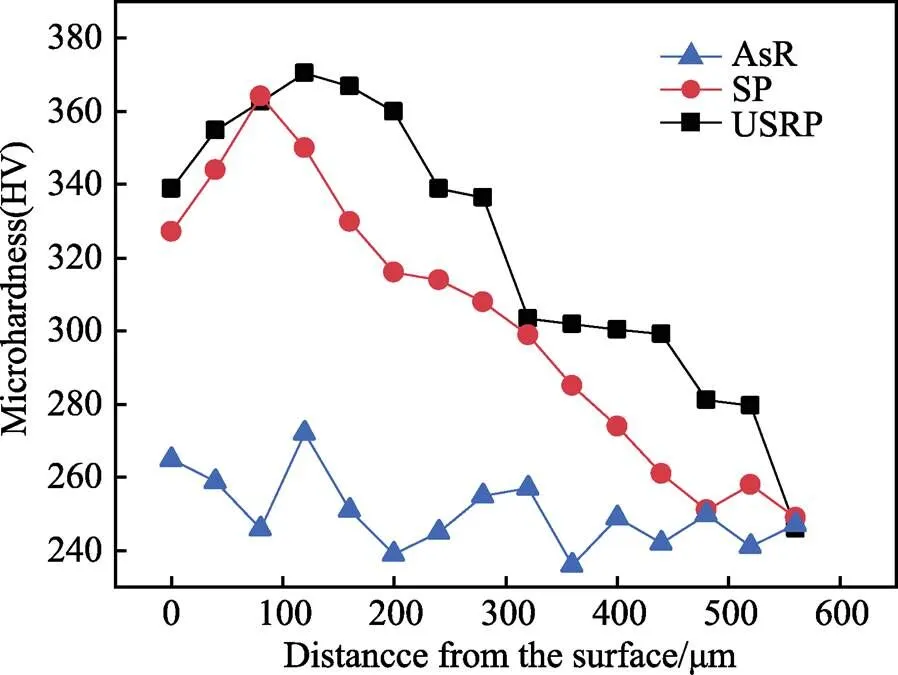
图3 不同表面处理后试样显微硬度分布
1 有限元模型
1.1 二维柱面/平面接触模型
在有限元软件ABAQUS中建立如图4所示的微动磨损的二维柱面/平面接触模型,圆柱面的半径为4 mm,下试件的长宽分别为10 mm和2.5 mm。Tobi等[22]认为,在微动磨损过程中由磨损所致使的接触几何的变化会使得在接触区域发生塑性损伤,因此在发生塑性损伤时需考虑循环塑性的影响,故文中所选取的材料属性见表1。设置平板为变形体,圆柱设置为刚体。边界条件为平板左端固定,底部设置为轴对称边界条件,在参考点上施加法向载荷使两试件紧密接触。图4中,为圆柱试件施加的切向周期性位移载荷,使两试件相对滑动,产生微动磨损。为保证2个试件接触计算结果的收敛性,有限元模型采用四节点平面应变单元CPE4。由于接触边缘附近存在明显的应力集中现象,为了能有效地捕捉接触区域的应力变化以及精确地获得该部位重要的微动参量,需要网格尺寸朝接触区域逐渐细化,该区域细化后的网格单元为5 μm×5 μm。
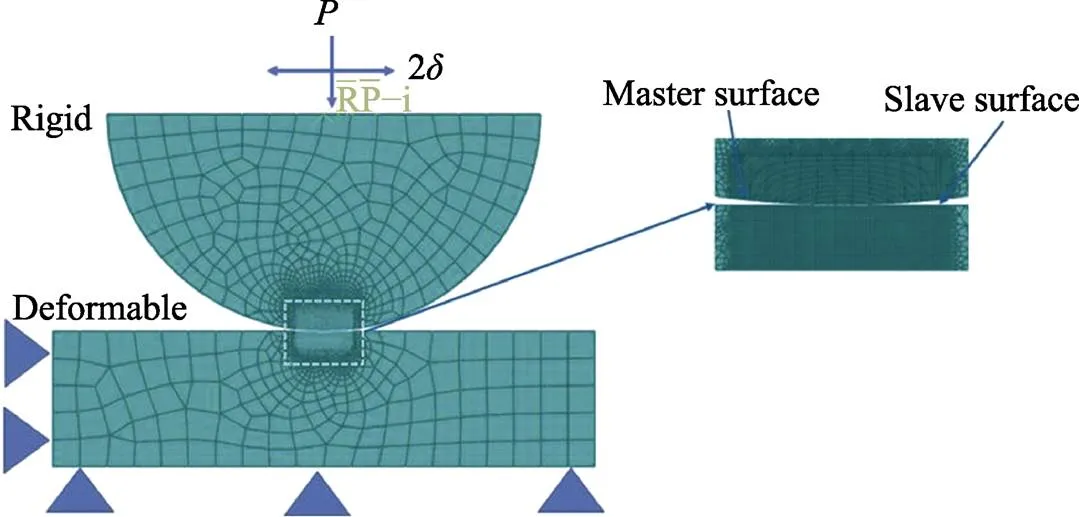
图4 有限元模型及边界条件
表1 TC4的力学性能和材料参数

Tab.1 Mechanical properties and material parameters for TC4

1.2 模型加载历程
二维柱面/平面微动磨损有限元模型的加载过程如图5所示。磨损过程包括3个分析步:
1)对平板试样下端进行对称约束,左端全约束,考虑到接触属于非线性问题,若一开始就施加较大的法向载荷,易造成计算不收敛,故在圆柱顶面中点处施加较小的法向载荷0,使两试样进行预接触。若对于强化后的试样,则还需在模型中引入强化后的残余应力场和等效塑性应变场。
2)保持模型原有约束不变,将原来的法向载荷0改为最终需要施加的法向载荷,并在后续的磨损过程中持续以恒定值施加,使得平板试样与圆柱试样在整个微动过程中一直保持良好的接触状态。
3)在圆柱顶面中点施加周期性的位移条件,幅值为。在最后一个时间分析步,需要将法向载荷进行卸载,即载荷逐渐减小为0,以获得更准确的微动参量数据。

图5 法向载荷、滑移距离加载历史
1.3 基于赫兹接触理论的有限元验证
在微动磨损仿真分析之前,需要对二维平面/柱面有限元模型进行仿真验证,以确保后期的微动磨损仿真结果真实有效。首先对建立好的二维模型进行受力分析,并将仿真结果与赫兹弹性接触理论进行对比,进而验证仿真结果的有效性。
赫兹接触应力公式[23]为:
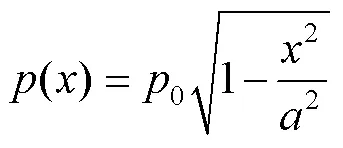
式中:为接触区域的半宽度;0为最大的接触压力。

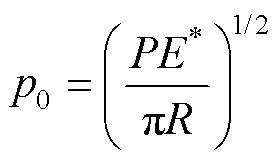
式中:为施加的法向载荷;*为两接触体材料复合弹性模量。对于平面应变问题,*可用式(4)表示。

式中:f、c和f、c分别为圆柱和平面的弹性模量和泊松比。
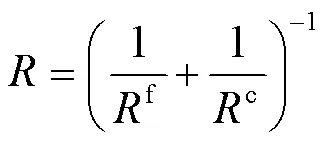
式中:f、c分别为柱面和平面的曲率半径,对于柱面来说,其曲率半径趋于无穷大。
接触压力的验证结果如图6所示,可见接触压力的仿真结果与理论值非常接近。由此可知,有限元法适合求解有限接触长度的问题,且该有限元模型在接触区域的网格非常精细,能够对接触区域的微动参量以及应力集中现象进行较为理想的表征。
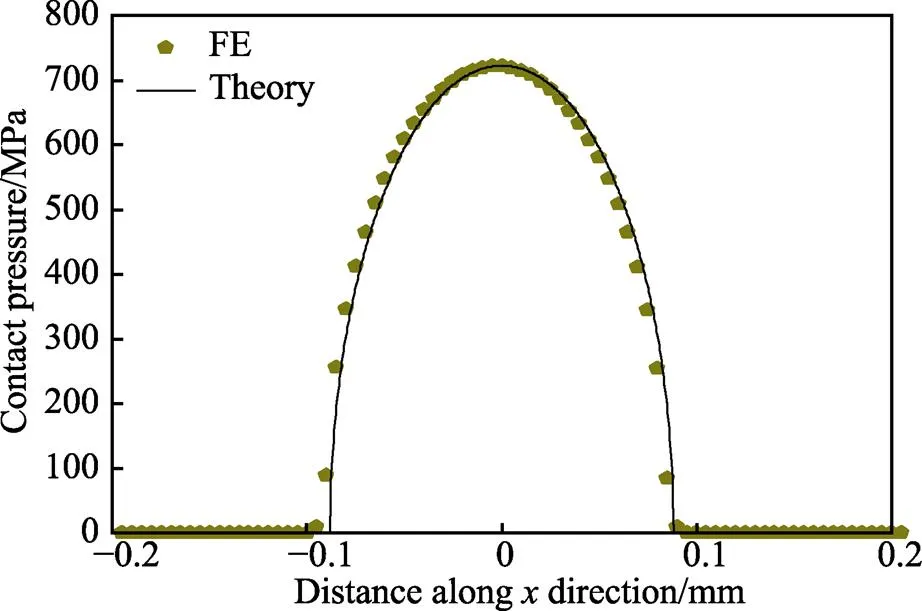
图6 接触压力的数值解和理论解的对比(法向载荷为100 N)
2 磨损方法
在对微动磨损进行有限元模拟时,主要的难点就是需要对被磨损面的材料去除进行准确的表征,也就是说,在实际工程中,两接触体在外力作用下因发生相对滑动而导致的材料损失在有限元中该如何实现。一般来讲,改进的Archard磨损方程和能耗模型可以很好地表征接触体在外力作用下的磨损量,但由于能耗模型需要获得大量的剪切摩擦力–滑移量数据,且要求较大的釆样密度,再通过积分获得能耗值,所以应用偏少,故本文选用改进的Archard磨损方程。从式(6)可知,材料的磨损量与法向载荷及滑移距离成正比关系,与材料的局部硬度为反比关系。

式中:为总磨损量;为滑动距离;为磨损系数;为法向载荷;为材料的硬度。
为了能够在有限元在中使用该方程,需要对其进行改进。对于有限元模型,接触面节点处的磨损深度d()的表达式为:


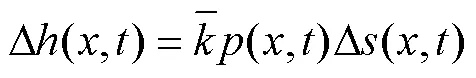
通常来说,工程中的微动磨损周次都是成千上万周的,甚至有上百万周的,如果磨损仿真中的1个分析步仅代表1次循环载荷的作用,那么对如此之多的磨损周次将会是非常耗费计算时间的。由于1次微动磨损对磨损面的磨损效果非常小,无法对接触面轮廓造成明显变化,对仿真计算中的微动参量几乎不会产生任何影响。因此,在进行磨损仿真时,完全没有必要对每个循环载荷作用后的磨损轮廓进行更新。目前学者们已经提出了几种方案来提高磨损仿真的计算效率,其中循环跳跃技术为大部分学者所采用。循环跳跃技术是利用仿真中单次循环来代替试验中的Δ次循环,故适用于仿真分析的Archard的修正形式为:
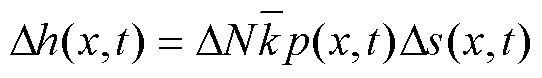
通常来讲,较小的循环跳跃值能使时域更好的离散化,从而有助于保持仿真的稳定性和准确性;而较大的循环跳跃值能够大大节省计算时间,但有可能造成收敛困难。最终,通过反复调试,选择使用循环跳跃值为2 000,因为它能够很好地兼顾计算效率、稳定性以及准确性。
在ABAQUS有限元软件中,材料的去除并不是通过删除单元或节点来实现的,而是通过对从面接触节点的强制偏移来实现的。这种强制偏移会导致网格单元发生过度畸变,甚至会产生负体积,最终导致收敛困难,而ALE自适应网格技术可以很好地解决此问题,具体过程如图7所示,而对于微动磨损的表征如图8所示。

图7 ALE自适应网格技术示意图
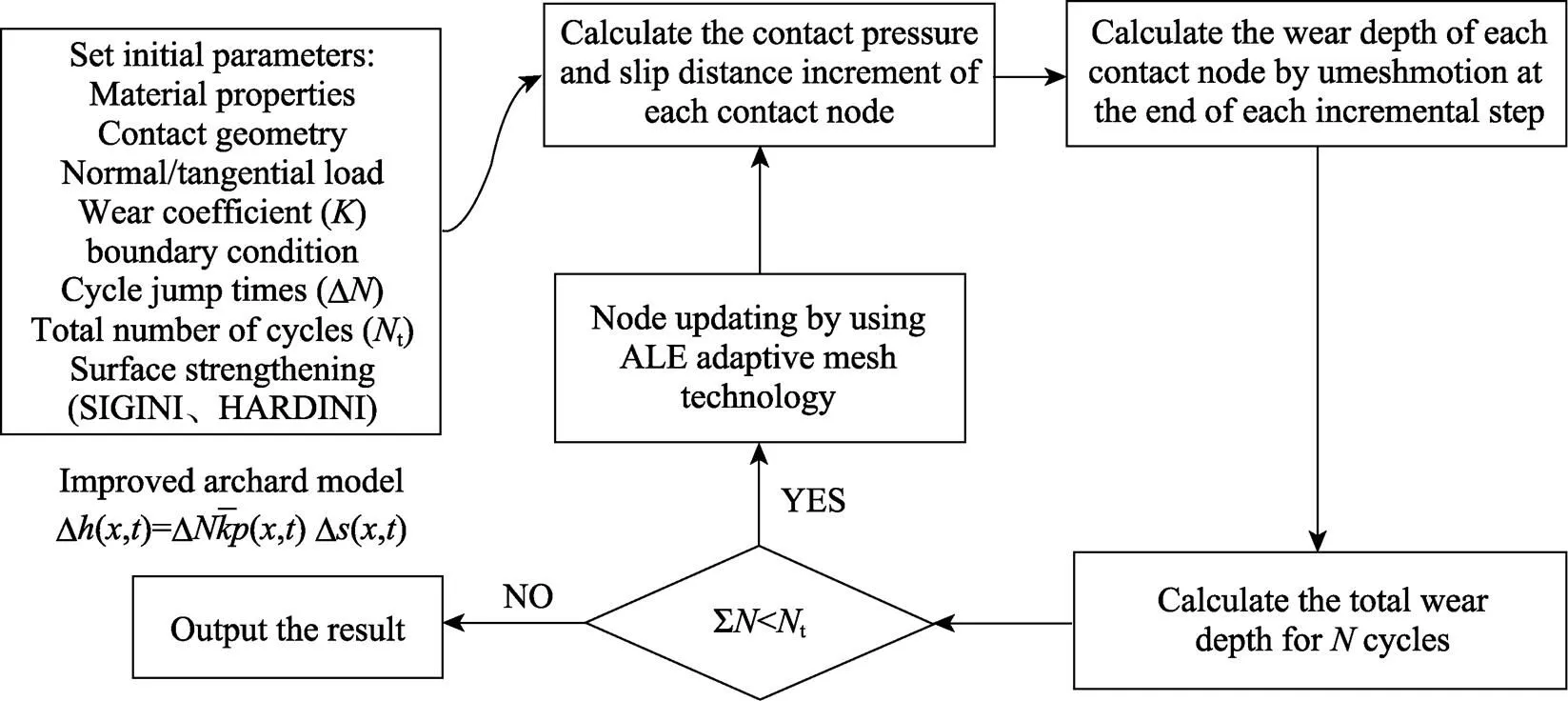
图8 磨损仿真路线
3 表面强化后不同因素对微动磨损性能的影响
诸如SP、USPR等表面机械强化工艺会使得试样的一些关键参数(如摩擦系数、残余应力场、塑性应变场和表面硬度等)发生改变。本文重点研究摩擦系数、残余应力场以及等效塑性应变场对接触参量以及接触区域应力应变分布的影响,尤其是接触边缘的塑性变形行为,因为塑性变形在表面裂纹形核及其裂纹在初期扩展中有显著影响。
3.1 摩擦系数对微动磨损性能的影响
在大多数的磨损仿真研究中,强化前后都是把摩擦系数当作一个定值来模拟,很少见到有仿真研究表征表面强化后摩擦系数改变的。但在实际工程中,经表面处理后,试样的表面状态肯定会发生改变。目前关于磨损仿真的文献大多采用的摩擦系数为0.6、0.8、0.9,至于摩擦系数不同的主要原因是原试样的处理
工艺不尽相同。本文中并不讨论原始试样摩擦系数的准确值,只考虑表面强化对原始试样摩擦系数的改变情况,以及对微动磨损性能的间接影响。考虑到如果摩擦系数相差较小,它们之间的微动参量或者应力状态可能变化得并不明显,故选择让各摩擦系数之间相差的较大一些。加之由试验发现原试样经SP处理后,粗糙度增加,而经USRP处理后,粗糙度得以降低,最终AsR、SP及USR试样的摩擦系数分别选择为0.6、0.9、0.3。
模型接触中心磨损深度值在不同摩擦系数下随循环周次的变化情况如图9a所示。可以看出,磨损深度都随着循环周次的增加而不断增大。这是因为随着微动的不断进行,接触表面的材料会不断地脱落,从而造成材料的损失,且最终会趋于一个动态平衡状态,即磨损量不会再随着微动循环次数继续增加。这可能是因为此时试样由于材料损失过大而发生了断裂,从而终止了磨损过程。除此之外,在磨损初期,3种摩擦状态下的磨损量相差较小,随着循环次数的增多,磨损量也相差得越来越多。其原因可能是在早期阶段,材料表面的金属氧化膜起到了一定的抗磨损作用,但随着磨损的不断进行,金属氧化膜被消耗掉变成了碎屑,或者变成第三体,加速磨损过程,且摩擦系数越大,磨损越严重。
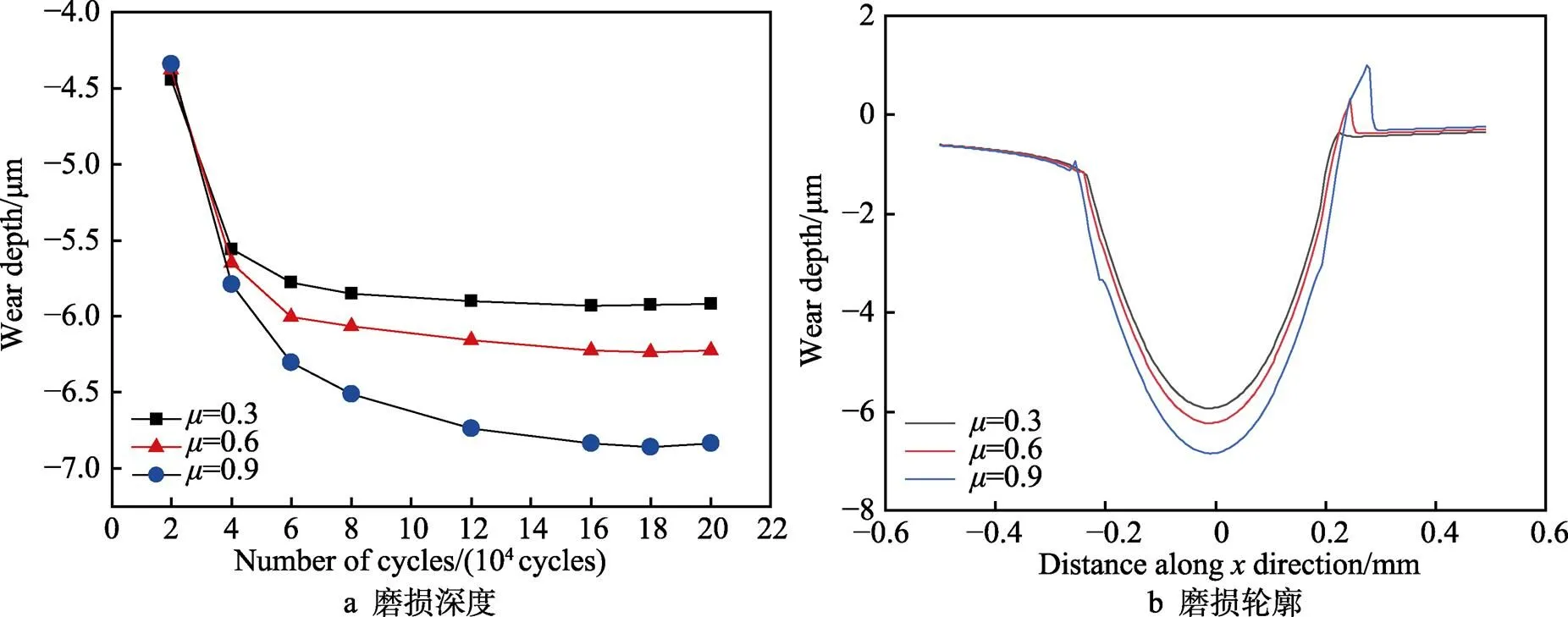
图9 不同摩擦系数下随循环周次变化的磨损深度和第20万周次时的磨损轮廓
从图9b中可以看出,SP试样在左侧大约–0.255 mm处有轻微的凸起,表明此时已经产生了微小的塑性变形。这主要是因为此处位于高接触应力区,且摩擦系数也较大,两者的联合作用使得该处区域达到了剪切屈服的临界值。对于USRP试样和AsR试样,尽管也处于高应力区,但由于摩擦系数不够,未达到剪切屈服,因此没有明显的塑性变形。相较于左侧,大约在右侧0.267 mm区域,不管是处于何种摩擦状态,试样都发生了明显的塑性变形,且摩擦系数越大,塑性变形程度越明显,这是因为该区域处于高磨损状态。除此之外,磨损轮廓还会随着摩擦系数的增大而逐渐往外侧偏移,并且接触中心区域的磨损深度也随着摩擦系数的增大而越来越深。其主要原因是摩擦系数越大,其表面的微凸体越多,且间距越大,这就使得相邻之间微凸体的结合力不够,容易导致材料在微动过程中发生脱落,从而造成接触面间材料的损失。随着微动循环次数逐渐增加,磨损深度也变得更深。与此同时,接触边缘磨损痕迹也呈现出逐渐往外侧偏移的趋势。由于循环往复的挤压,接触区域最边缘的部位发生了明显的塑性变形,最终导致该部位的轮廓明显变高。
较高的摩擦系数会引起材料的表面塑性变形,从而加剧表面磨损。当摩擦系数变高时,整个接触表面就会产生较为明显的宏观塑性变形,此时最大当量应力将会分布在整个接触表面上,从而引起严重的磨损现象。对于较高的摩擦系数,磨损量也将会变得越高,这就表明当其他条件一定时,摩擦系数的增加会使得磨损量大幅提高,这是因为累积的塑性耗散能会导致材料的迅速退化。此外,材料接触表面以及亚表面区域的循环变形行为对微动磨损影响显著。因为在磨损过程中,微动区域内的应力重分布和材料的循环塑性变形行为息息相关,尤其是塑性变形中的棘轮行为,它极易导致材料接触区域发生延性耗竭和诱发表面裂纹的萌生,从而导致分层磨损。由此可推断出摩擦系数越大,塑性耗散能就越高,材料也就越容易发生磨损。
从图10 a1、b1、c1中可知,塑性变形会随着摩擦系数的增加而变得明显,与此同时,塑性变形的区域也变得越来越大。也就是说,当微动区域的接触应力处于高应力状态时,摩擦系数与切向载荷呈正比例关系,摩擦系数越大,切向载荷也就越大,就越容易发生塑性累积的现象,甚至发生明显的剪切屈服。另外,最大塑性应变通常出现在微动接触边缘,这是因为接触表面处于复杂的高应力区,有很严重的应力集中现象,而且该区域还是磨损与未磨损的边界处,为典型的几何不连续处。高塑性应变的区域正好与磨损引起的接触边缘相对应,并且高塑性应变是由切向载荷引起的,而不是由法向载荷引起的,这称为“犁沟”效应。此外,图10a1、b1、c1中左右两侧的塑性应变区域基本是对称的,这是因为试样和加载条件也是对称的,至于两侧塑性应变存在差别的原因主要是两侧滑移距离的不同,这就导致两边区域的几何变形也不相同。由图10 a2、b2、c2中可知,接触边缘左右两侧塑性应变都是随着循环周次而不断增加的,这就说明塑性变形是可以累积的。对于USRP试样,左右两侧塑性应变随着磨损周次呈抛物线形式逐渐递增,且左右两侧塑性应变差值随着循环周次越来越大。除此之外,左侧的塑性应变逐步趋于平稳,而右侧的塑性应变仍有继续累积的趋势。AsR和SP试样左右两侧塑性应变几乎是随着磨损周次呈线性递增的,且左右两侧塑性应变差值也是越来越大。在第20万周的时候,AsR、SP试样右侧的塑性应变值都为左侧的2倍左右,而USRP试样右侧的塑性应变值为左侧的5倍左右。由此可推测出,在特定的工况下,高摩擦系数会降低两侧塑性应变比值。综上所述,塑性应变不仅与应力状态、循环次数有关,还与摩擦状态、滑移距离比值相关。

图10 不同摩擦系数下随磨损周次变化的等效塑性应变分布及其最值
3.2 残余应力场对微动磨损性能的影响
大多数的研究都表明,残余应力对裂纹的萌生有阻碍作用,即残余应力能够有效地提高材料的抗疲劳能力,但目前关于残余应力对微动磨损性能影响的研究却鲜有报道。本文通过将残余应力场纳入到磨损仿真之中,研究其对微动磨损的影响规律,残余应力场的相关数据通过试验得到。考虑到残余应力沿深度方向呈梯形分布,故可对试验中所测得的残余应力值通过数据拟合的方式求解出来。将残余应力通过编写初始残余应力场子程序SIGINI的方式引入到磨损仿真中,其中SP、USRP试样对应的初始残余应力场分布如图11所示。考虑到微动磨损量级大多为微米级,加上离表面距离过远的残余应力对表面的应力应变分布影响微乎其微,故此处的初始残余应力场的深度只考虑到0.3 mm。考虑到已有的文献大多都采用摩擦系数为0.8来研究微动磨损仿真,故采用相同的摩擦系数0.8。
由图12a可知,引入残余应力场后,磨损深度明显减小,USRP、SP试样的磨损深度相比AsR试样分别降低15%、10%。由此可知,USRP要比SP的抗磨损效果更为显著。在引入残余应力场前后,试样接触中心的磨损深度都随着循环周次的增加而逐渐变深,且变化趋势基本相同。在磨损早期,磨损深度变化较大,而到了中后期却变化得很平缓,逐渐有趋于饱和的趋势。从图12b可以看出,在引入残余应力场前后,试样接触区域边缘都发生了塑性累积的现象,但引入残余应力场后,表面的弹性变形得以部分回复。因为经SP、USRP处理后,试样表面引入了残余压应力,它能够很好地抵消一部分外载荷对材料的作用,从而减小基体材料的弹性变形。至于接触中心区域的磨损,是因为在最终变形机制中材料的损失比弹塑性变形更占优势,而相较于接触边缘的塑性应变现象,这可能是因为存在边缘效应。另外,圆柱面的滑移距离也没有超过接触边缘,故边缘也不会产生所谓的材料的损失,反而因为存在较大的剪切力,使得该区域为实现材料内部的平衡状态而发生了形变,从而呈现出凹坑状的磨损轮廓。

a SPb USRP

图12 不同残余应力场下随循环周次变化的磨损深度值和第20万周次时的磨损轮廓
根据图13a1、b1、c1可知,随着残余应力场的引入,塑性应变最值的位置逐渐向两侧边缘移动。此外,不管是否引入残余应力场,磨损轮廓都会随着磨损周次向外延伸,且两侧相对移动的距离几乎相等。这可能是因为施加残余应力场的磨损区域是关于接触中心对称的,且对于有限元分析来说,里面的材料属性也是均质且各向同性的。除此之外,加入残余应力场后,虽然试样左侧的等效塑性应变得到了增加,但右侧的等效塑性应变值也发生了改变,且在整个磨损过程中都是降低的。这就说明残余应力间接地影响到了材料内部塑性应变的流动,使得右侧的高塑性应变流向左侧较低的塑性应变,从而达到内部塑性应变场的自相平衡,并且仿真中所采用的线弹性理论是非线性随动强化准则,它能很好地体现塑性应变场在外力作用下的准确变化。另外,SP和USRP试样之间的等效塑性应变值相差较小,这主要是因为2种强化工艺在材料表面所引入的残余应力场相差较小,虽然SP、USRP试样在离表面较远处区域的残余应力场相差较大,但对表面的微动参量影响效果并不明显,说明残余应力对微动参量的影响取决于残余应力的深度及最大值的综合影响。在给定的残余应力最大值的情况下,它所在的位置离接触表面越近越好,而在给定的影响深度下,残余应力值越大越好,因为这样能更好地抑制裂纹的萌生以及对微动参量产生明显的影响。图13 a1、b1、c1的塑性应变与图12b中磨损轮廓边缘的凸起形成了对应。至于接触中心区域没有发生明显的塑性累积现象,有可能是因为随着微动循环次数的增加,磨损所导致的接触几何发生变化以及接触顺应性的增加,使得接触中心的塑性累积现象消失,也有可能是因为接触中心处产生的剪切力较小,达不到剪切屈服的临界点,从而使得产生剪切屈服塑性较小。图13b1和c1、图13b2和c2的塑性应变变化趋势比较类似,这是因为这2种试样表层及亚表层所引入的残余应力场相差不大,表明该变量对残余应力的变化不敏感。
3.3 等效塑性应变场对微动磨损性能的影响
目前对于塑性应变场对微动磨损性能的影响规律研究甚少,因此需要对等效塑性应变场与微动磨损之间的相互影响机制及接触区域中塑性应变的演化有更深入的了解。考虑到由表面强化所带来的塑性应变实测困难,目前相关的文献中还没有相关的试验数据可供借鉴。有研究[24]提出,显微硬度可直接反映试样表面加工硬化的历程,进而表征表层加工硬化程度及塑性变形影响深度,故在此用Liu等[25]提出的喷丸等效塑性应变经验公式表示相应的塑性应变场。

式中:0为表面的塑性应变值(=0);0为塑性应变为0时的深度;为塑性应变非单调变化的参数;是用来描述塑性应变分布沿深度变化的参数。
一般来说,SP处理会产生很高的塑性应变(高达30%~40%)。因此,表面的塑性应变,即0范围为0.3~0.4。在本研究中,假设塑性应变的深度0与残余压应力的初始深度相同。从USRP和SP试样的显微硬度曲线可以看出,这种强化工艺引入的显微硬度相差不大,故可假设在该USRP工艺参数下,USRP和SP试样产生的表面塑性应变范围也在0.3~0.4。借助试验所测的显微硬度分布,并结合式(10)得出图14所示的初始等效塑性应变分布。
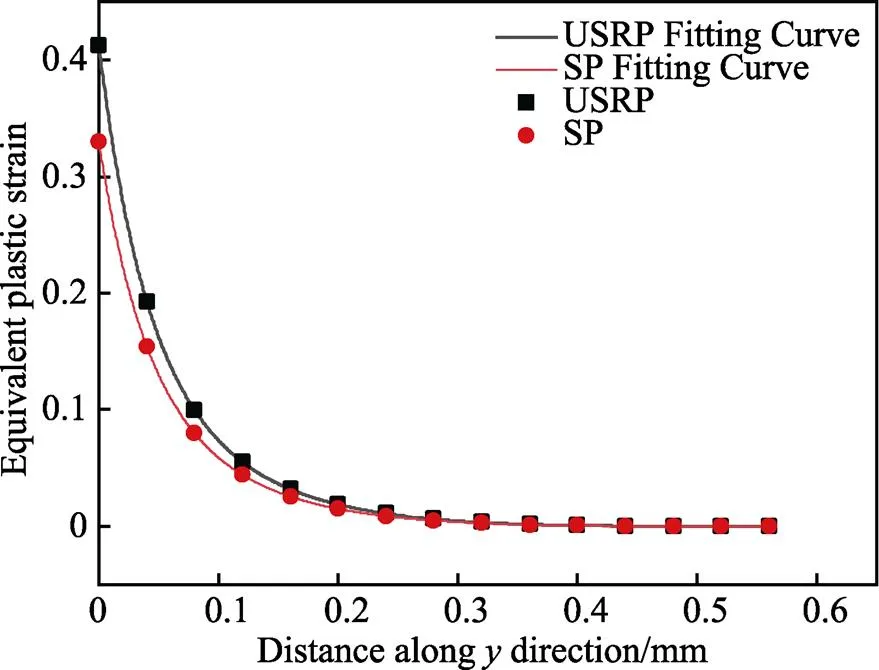
图14 不同表面强化所引入的初始等效塑性应变场分布
考虑到塑性应变场是沿深度方向是梯度分布的,可对塑性应变值通过数据拟合的方式求解出来。本文将塑性应变场通过编写初始等效塑性应变场子程序HARDINI的方式引入到磨损仿真中,其中SP、USRP试样对应的塑性应变场分布如图15所示。从塑性应变场沿深度的分布曲线可知,大概在深度0.3 mm后的塑性应变场几乎为0。故为了提高仿真效率,同时也是为了与残余应力场深度保持一致,选择0.3 mm作为塑性应变场的影响深度。
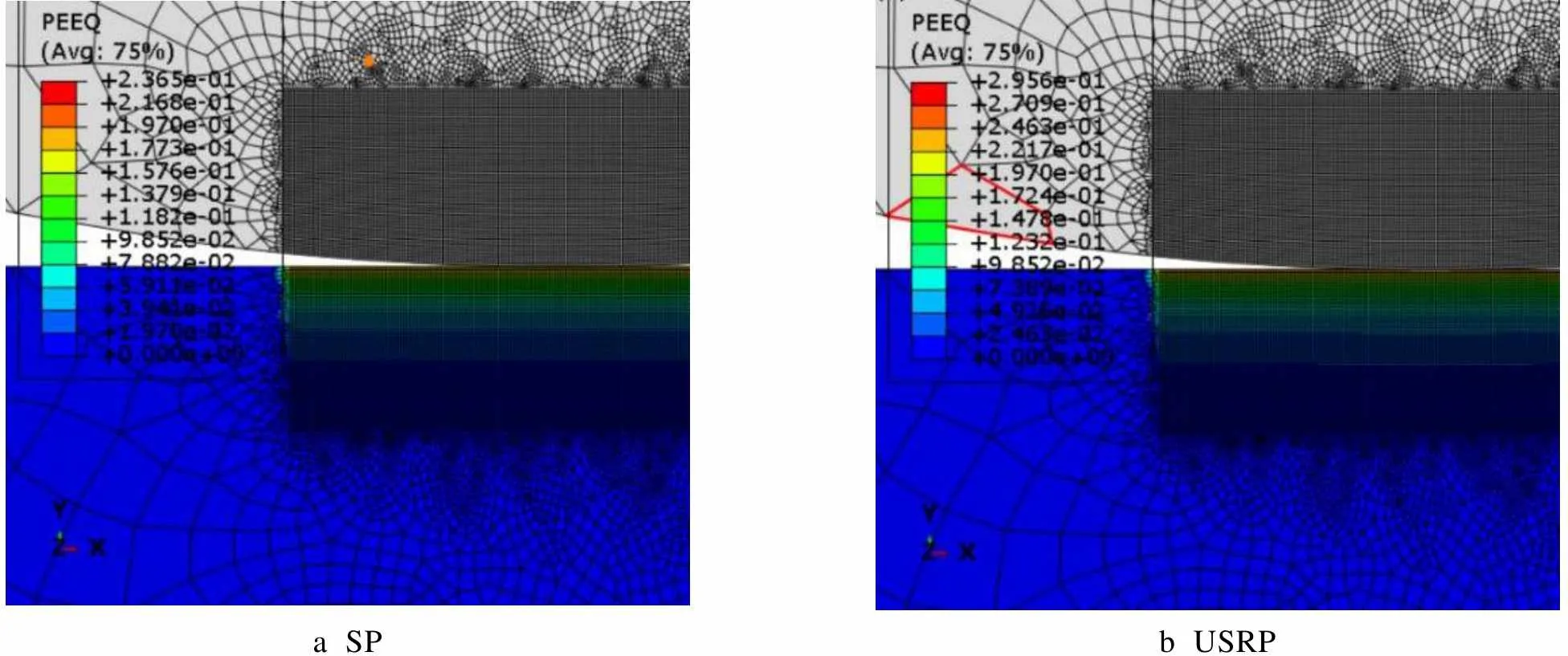
a SPb USRP
不同塑性应变场下,磨损深度的变化值以及第20万周次沿轴的磨损轮廓随循环周次的变化如图16所示。由图16a可知,引入塑性应变场前后,磨损深度都随着循环周次呈抛物线形式逐渐增加,大概到从第16万周次开始,磨损量逐渐趋于饱和。其原因可能是:由于磨损量较大,加上裂纹的作用已经达到了断裂的临界点;由于接触面间往复相对移动,产生的磨屑在接触边缘难以溢出,新产生的磨屑充当填充物留在原来的磨损坑中,使得磨损量难以继续增加。从图16b可知,引入塑性应变场后,磨损深度得以明显减小,大概降低了6%,其影响效果明显弱于残余应力场。这可能是因为所采用的磨损公式是和应力分布相关的,对应变的分布不敏感,再加上引入的应变也是比较小的,因此引入的塑性应变场对磨损量的影响本身就比较弱。同时可以看出,即使引入了塑性应变场,左侧的塑性应变依然很小,甚至可以说是几乎没区别,而右侧的塑性应变有较为明显的变化,使得磨损轮廓往接触中心方向移动。由此可知,在高塑性区,塑性应变场不仅可以减小微动磨损痕迹,还可以降低塑性累积效果。
不同塑性应变场下,沿水平方向随循环周次变化的塑性应变分布以及在不同周次的塑性应变最值如图17所示。从图17a1、b1、c1中可以清晰地看到,引入塑性应变场后,左右两侧的塑性应变区域向接触边缘外侧偏移了0.1 mm左右。这与图16b中磨损痕迹的偏移方向恰恰是相反的,相同的是塑性应变值在引入塑性应变场后明显降低。一般认为塑性应变幅值的变化与应变强化成反比,即应变强化会减轻接触边缘由于循环加载而导致的塑性应变。另外可以从图17b、c看出来,SP和USRP试样的等效塑性应变值变化几乎一样,这是因为文中所得出的深度方向的塑性应变变化曲线是根据显微硬度变化趋势而来的,试验中测得的2种试样的显微硬度在表面相差很小,再加上显微硬度与塑性应变的公式转换,就使得塑性应变曲线更加接近。从图17 a2、b2、c2中可知,在引入塑性应变场之前,AsR试样左右两侧的塑性应变都是随着循环周次线性增加的,且在第2万周次就已经出现了塑性累积现象;而引入塑性应变场后,SP、USRP试样直到第4万周次才开始出现塑性应变,由此可知塑性应变场对塑性累积有延迟效果。另外,还观察到在这2种试样第4万周次之后的塑性应变累积与循环周次呈线性增加,左右两侧的塑性应变差值在引入塑性应变场之后也得以显著降低,大约降低了35%,且左右两侧的塑性应变差值随着循环周次的增加而增加。

图16 不同等效塑性应变场下随循环周次变化的磨损深度和第20万周次时的磨损轮廓

图17 不同等效塑性应变场下随磨损周次变化的等效塑性应变分布及其最值
4 微动疲劳试验
微动疲劳试验是通过对INSTRON疲劳试验机加入微动磨损装置(如图18所示)来实现的。INSTRON疲劳试验机主要是提供轴向拉–拉疲劳载荷,为正弦加载,频率为10 Hz,应力比为0.1。设置的单卡头微动磨损装置(见图19)主要是为了提供平稳恒定的法向载荷,其中法向载荷主要通过实时数显扭矩扳手来施加,应力环上左右对称的4个螺钉主要是为了与底板连接,从而保证整个机构能够平稳的固定在托盘之上。两侧的固定栓是对螺栓杆进行固定支撑,同时也是为了防止在试验过程中螺栓杆产生过大的晃动。

图18 微动疲劳装置
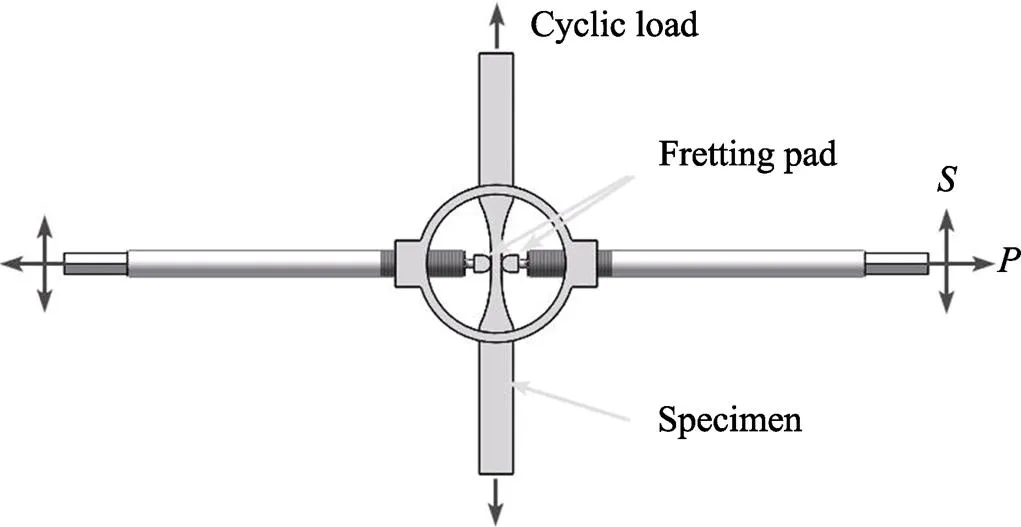
图19 微动磨损装置
AsR、SP、USRP平板试样的微动疲劳(Fretting Fatigue,FF)-曲线如图20所示。可以看出,AsR、SP、USRP试样的微动疲劳寿命都随着应力水平的增加而降低,并且应力水平越低,强化效果越显著。USRP试样对微动疲劳寿命提高得最为明显,因为USRP试样的表面粗糙度和表面显微硬度得到很大改善,这能很好地提高试样的抗磨损能力以及减轻应力集中,再加上较深的残余应力,从而大幅提高了试样的微动疲劳寿命。相比之下,SP试样对TC4钛合金微动疲劳寿命的提高效果却并不明显。一般来说,摩擦系数较大的部件更易受到微动损伤,尤其是对微动磨损较为敏感的钛合金。Bagherifard等[26]在研究喷丸对金属材料疲劳强度的影响时发现,较高的残余压应力和纳米晶体结构都有助于提高疲劳强度,但SP带来的高粗糙度会大大削弱上述2种有益参数的影响。
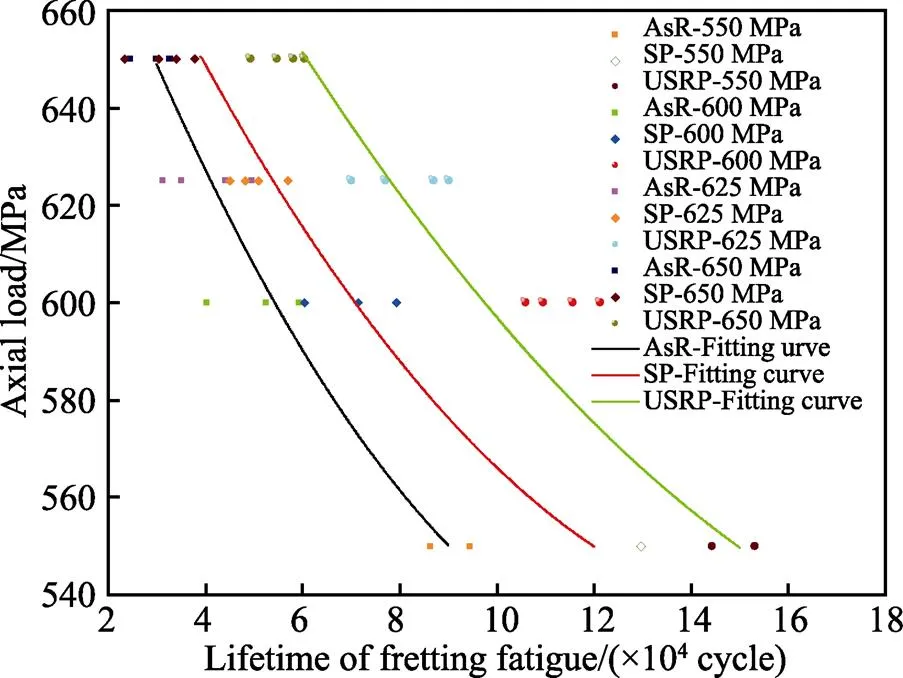
图20 不同表面强化下的微动疲劳寿命
AsR试样的微动疲劳寿命和普通疲劳(Plain Fatigue,PF)寿命柱状图见图21。可以看出,轴向应力幅值为600 MPa水平下的普通疲劳寿命为80多万周次,而在同应力水平下的微动疲劳寿命大概为8万周次,寿命大约降低了90%。在650 MPa应力水平下,寿命也降低了75%左右,即在每一个应力水平下,试样的PF寿命都比其FF寿命高得多。由此可知,TC4合金对微动损伤极为敏感,这可归因于与外部因素相关的严苛工况条件以及材料的内部原因。由于高应力集中,接触区域的微动行为会严重损伤试样的表面完整性,而且TC4容易发热,接触区域的微动磨损导致局部温度升高,这也会严重损坏表面材料。另外,还可以看出轴向应力越低,微动损伤效果越明显,可能是因为在微动疲劳过程中,微动磨损起到的作用越来越明显,在整个微动疲劳过程中,微动磨损占了主导地位。
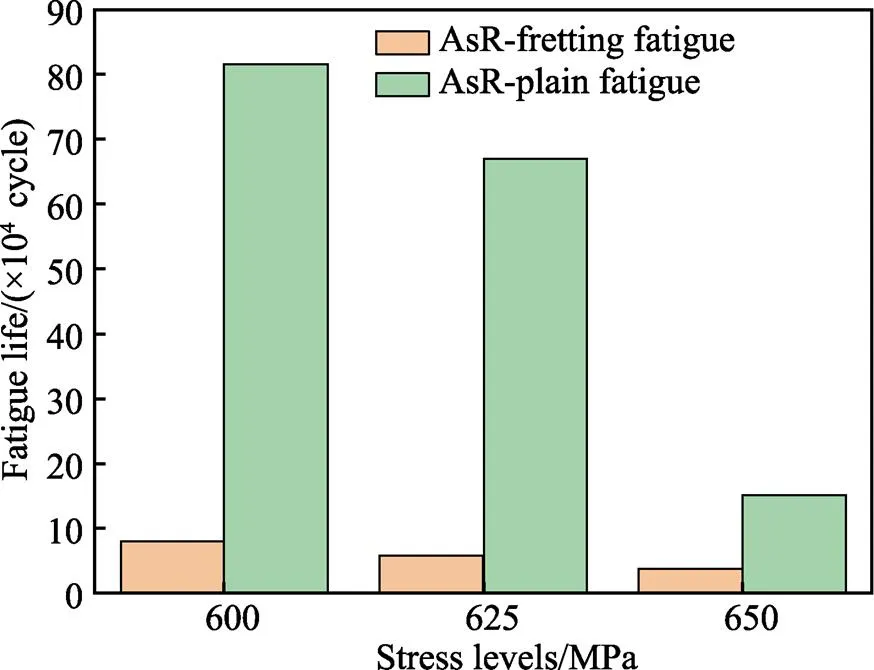
图21 不同应力水平下微动疲劳寿命和普通疲劳寿命
5 结论
在ABAQUS中建立微动磨损的二维柱面/平面接触模型,借助ABAQUS中的子程序SIGINI和HARDINI,分别将残余应力场、塑性应变场引入到表征微动磨损的UMESHMOTION子程序中,从而实现表面强化后不同摩擦力、残余应力场以及塑性应变场的有限元微动磨损仿真,得出以下结论:
1)试验中AsR、SP及USRP试样的摩擦系数分别取为0.6、0.9以及0.3。在磨损初期,3种摩擦状态下,磨损量相差较小,随着循环次数的增多,磨损量也相差的越来越多,且摩擦系数越大,磨损越严重。磨损轮廓还会随着摩擦系数的增大而逐渐往外侧偏移,接触中心区域的磨损深度也随着摩擦系数的增大而越来越深。
2)引入残余应力场后,磨损量得以显著减少,S,和USRP试样分别减少了10%和15%。在引入残余应力场前后,试样接触区域边缘都发生了塑性累积的现象,但引入残余应力场后,表面的弹性变形得以部分回复。因为经SP、USRP处理后,试样表面引入了残余压应力,它能够很好地抵消一部分外载荷对材料的作用,从而减小基体材料的弹性变形。
3)引入塑性应变场后,磨损量得以减小,但效果不如残余应力场。这是因为磨损仿真中采用的是Archard磨损公式,它是与应力分布相关的,对应变的分布不敏感,再加上引入的应变也是比较小的,因此引入的塑性应变场对磨损量的影响本身就比较弱。引入塑性应变场,左侧的塑性应变依然很小,甚至可以说是几乎没区别,而右侧的塑性应变有较为明显的变化,使得磨损轮廓往接触中心方向移动。由此可知,在高塑性区,塑性应变场不仅可以减小微动磨损痕迹,还可以降低塑性累积效果。
4)对比原试样的微动疲劳和普通疲劳寿命可以看出,加入微动磨损作用后,试样寿命显著降低,其中在应力水平600 MPa时,寿命降低效果最明显,大约降低了90%,而在650 MPa时降低了75%。此外,USRP试样的抗磨损效果最好。
[1] 周仲荣, LEO Vincent. 微动磨损[M]. 北京: 科学出版社, 2002.
ZHOU Zhong-rong, LEO Vincent. Fretting Wear[M]. Beijing: Science Press, 2002.
[2] MAJZOOBI G H, AHMADKHANI A R. The Effects of Multiple re-Shot Peening on Fretting Fatigue Behavior of Al7075-T6[J]. Surface and Coatings Technology, 2010, 205(1): 102-109.
[3] 沈明学, 彭金方, 郑健峰, 等. 微动疲劳研究进展[J]. 材料工程, 2010, 38(12): 86-91.
SHEN Ming-xue, PENG Jin-fang, ZHENG Jian-feng, et al. Study and Development of Fretting Fatigue[J]. Journal of Materials Engineering, 2010, 38(12): 86-91.
[4] NOWELL D, DINI D, HILLS D A. Recent Developments in the Understanding of Fretting Fatigue[J]. Engineering Fracture Mechanics, 2006, 73(2): 207-222.
[5] 同长虹, 黄建龙, 胡玉霞. 基于运动副磨损和原始误差影响的机构运动可靠性分析[J]. 兰州理工大学学报, 2010, 36(2): 33-37.
TONG Chang-hong, HUANG Jian-long, HU Yu-xia. Reliability Analysis of Mechanism Motion Based on both Wear of a Kinematic Pair and Its Original Error[J]. Journal of Lanzhou University of Technology, 2010, 36(2): 33-37.
[6] BUDINSKI K G. Tribological Properties of Titanium Alloys[J]. Wear, 1991, 151(2): 203-217.
[7] WANG Hai-bo, SONG Guo-lin, TANG Guo-yi. Effect of Electropulsing on Surface Mechanical Properties and Microstructure of AISI 304 Stainless Steel during Ultrasonic Surface Rolling Process[J]. Materials Science and Engineering: A, 2016, 662: 456-467.
[8] ZENG Y S. Application of Shot Peening Technology in the Development of Integral Panels of Civil Aircraft[J]. Aeronautical Manufacturing Technology, 2008(1): 54-55.
[9] FERNÁNDEZ PARIENTE I, GUAGLIANO M. About the Role of Residual Stresses and Surface Work Hardening on Fatigue ΔKTH of a Nitrided and Shot Peened Low-Alloy Steel[J]. Surface and Coatings Technology, 2008, 202(13): 3072-3080.
[10] LIU Dan, LIU Dao-xin, ZHANG Xiao-hua, et al. Plain Fatigue and Fretting Fatigue Behaviors of 17-4PH Steel Subjected to Ultrasonic Surface Rolling Process: A Comparative Study[J]. Surface and Coatings Technology, 2020, 399: 126196.
[11] REN Zhao-jun, LAI Fu-qiang, QU Sheng-guan, et al. Effect of Ultrasonic Surface Rolling on Surface Layer Properties and Fretting Wear Properties of Titanium Alloy Ti5Al4Mo6V2Nb1Fe[J]. Surface and Coatings Technology, 2020, 389: 125612.
[12] KUMAR S A, RAMAN S G S, SANKARA NARAYANAN T S N, et al. Influence of Counterbody Material on Fretting Wear Behaviour of Surface Mechanical Attrition Treated Ti-6Al-4V[J]. Tribology International, 2013, 57: 107-114.
[13] FAN Na, WANG Yun-xia, WANG Qiu-feng, et al. Effect of Displacement Amplitude on Fretting Wear of 304 Stainless Steel in Air and Sea Water[J]. Lubrication Science, 2018, 30(3): 116-125.
[14] 张猛, 莫继良, 徐敬业, 等. 一种分析手指接触摩擦的新型试验装置[J]. 摩擦学学报, 2016, 36(6): 776-780.
ZHANG Meng, MO Ji-liang, XU Jing-ye, et al. A Newly Developed Experimental Device for Friction Analysis of Finger Touch[J]. Tribology, 2016, 36(6): 776-780.
[15] 王世洪, 梁佑明, 沈桂琴. TC11钛合金微动磨损及疲劳防护工艺的探讨[J]. 航空学报, 1996, 17(3): 379-382.
WANG Shi-hong, LIANG You-ming, SHEN Gui-qin. Research on the Protective Treatment for Fretting Wear and Fretting Fatigue of TC11 Titanium Alloy[J]. Acta Aeronautica et Astronautica Sinica, 1996, 17(3): 379-382.
[16] SZOLWINSKI M P, FARRIS T N. Mechanics of Fretting Fatigue Crack Formation[J]. Wear, 1996, 198(1/2): 93-107.
[17] TANG Li-chen, DING Shu-rong, QIAN Hao, et al. Fretting Fatigue Tests and Crack Initiation Analysis on Zircaloy Tube Specimens[J]. International Journal of Fatigue, 2014, 63: 154-161.
[18] YUE Tong-yan, ABDEL WAHAB M. Finite Element Analysis of Fretting Wear under Variable Coefficient of Friction and Different Contact Regimes[J]. Tribology International, 2017, 107: 274-282.
[19] 李玲, 康乐, 阮晓光, 等. 不同加载条件下柱面/平面微动磨损有限元分析[J]. 机械科学与技术, 2018, 37(12): 1854-1861.
LI Ling, KANG Le, RUAN Xiao-guang, et al. Finite Element Analysis of Cylinder-Flat Fretting Wear under Different Loading Conditions[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(12): 1854-1861.
[20] 张慧杰, 王志敏, 张太华. 微动工况下柱面不同因素对平面磨损显著性的分析[J]. 工具技术, 2019, 53(1): 47-50.
ZHANG Hui-jie, WANG Zhi-min, ZHANG Tai-hua. Analysis of Significance of Different Factors on Flat Wear under Mirco-Motion Conditionsrevoke[J]. Tool Engineering, 2019, 53(1): 47-50.
[21] ARNAB Ghosh, BEN Leonard, FARSHID Sadeghi. A stress based damage mechanics model to simulate fretting wear of Hertzian line contact in partial slip[J]. Wear, 2013, 307(1/2): 87-99.
[22] MOHD TOBI A L, DING J, BANDAK G, et al. A Study on the Interaction between Fretting Wear and Cyclic Plasticity for Ti-6Al-4V[J]. Wear, 2009, 267(1/2/3/4): 270- 282.
[23] JOHNSON K L. Contact Mechanics[M]. Cambridge: Cambridge University Press, 1985.
[24] 胡永会, 吴运新, 陈磊. 喷丸处理7075铝合金循环载荷下表面残余应力的松弛规律[J]. 材料研究与应用, 2010, 4(3): 174-179.
HU Yong-hui, WU Yun-xin, CHEN Lei. Residual Stress Relaxation of Shot Peened 7075 Aluminum Alloy under Cyclic Load[J]. Materials Research and Application, 2010, 4(3): 174-179.
[25] LIUA J, YUANA H. Computational Prediction of shot- Peening Induced Residual Stresses under Cyclic Loading[C]//Conf Proc: ICSP-10. Tokyo: [s. n.], 2008.
[26] BAGHERIFARD S, FERNANDEZ-PARIENTE I, GHELICHI R, et al. Effect of Severe Shot Peening on Microstructure and Fatigue Strength of Cast Iron[J]. International Journal of Fatigue, 2014, 65: 64-70.
Fretting Wear Properties of TC4 Alloy under Different Surface Strengthening States
,,,,
(Key Laboratory of Pressurized System and Safety, Ministry of Education, East China University of Science and Technology, Shanghai 200237, China)
The work aimed to study the effect of friction coefficient, residual stress field and plastic strain field on the fretting wear properties of TC4 alloy after shot peening (SP) and ultrasonic surface rolling process (USRP) strengthening. The surface of TC4 alloy was strengthened by SP and USRP respectively. After strengthening, the surface roughness, residual stress and microhardness of the TC4 alloy were measured by experiments. Based on the improved Archard wear equation, a two-dimensional cylindrical/planar contact model of fretting wear was established in the ABAQUS finite element software. With the help of the subroutines SIGINI and HARDINI in ABAQUS, the residual stress field and the plastic strain field were respectively introduced into the UMESHMOTION subroutine, so as to explore the effect of friction coefficient, residual stress field and plastic strain field on the surface fretting wear performance after surface strengthening. It was found that the surface roughness of the original specimen increased after SP, but improved after USRP; The microhardness of the specimen after SP and USRP strengthening was 1.28 times and 1.23 times of the original specimen, respectively. The maximum residual stress of TC4 alloy after USRP is –550 MPa, and after SP is –380 MPa. After introducing the residue stress field, the wear depth of the specimen was significantly reduced. Compared with the original specimen, the wear depth of the USRP and SP specimens were reduced by 15% and 10% respectively. After the introduction of the plastic strain field, the wear depth of the TC4 alloy is reduced about 6%. It can be concluded that the greater the friction coefficient, the more severe the wear under the same conditions. The wear profile gradually shifts to the outside with the increase of the friction coefficient, and the wear depth in the contact center area also becomes deeper and deeper with the increase of the friction coefficient. The plastic deformation behavior becomes more obvious with the increase of the friction coefficient and eventually makes the area of plastic deformation become larger and larger. With the introducing of residual stress field and plastic strain field, the amount of wear is reduced, and the influence of the residual stress is more significant. Through the fretting fatigue test, it is found that the life of the specimen is significantly reduced after the fretting wear is added, and the USRP specimen has the best anti-wear performance.
surface strengthening; fretting wear; residual stress field; plastic strain field; UMESHMOTION subroutine
TH115.5
A
1001-3660(2022)07-0127-14
10.16490/j.cnki.issn.1001-3660.2022.07.012
2021–04–21;
2021–09–27
2021-04-21;
2021-09-27
国家重点研发项目(2018YFC1902400);上海市自然科学基金项目(20ZR1415300)
National Key Research and Development Project (2018YFC1902400) and Natural Science Foundation of Shanghai (20ZR1415300)
刘柏(1996—),男,硕士研究生,主要研究方向为航空发动机叶片榫接结构的微动疲劳性能。
LIU Bai (1996-), Male, Postgraduate, Research focus: fretting fatigue performance of aeroengine blade tenon structure.
王宁(1980—),女,博士,副教授,主要研究方向为结构完整性、表面强化、蠕变及微动疲劳性能。
WANG Ning (1980-), Female, Doctor, Associate professor, Research focus: structural integrity, surface strengthening, creep and fretting fatigue of components.
刘柏, 王宁, 朱金龙, 等. TC4合金在不同表面强化状态下的微动磨损性能研究[J]. 表面技术, 2022, 51(7): 127-140.
LIU Bai, WANG Ning, ZHU Jin-long, et al. Fretting Wear Properties of TC4 Alloy under Different Surface Strengthening States[J]. Surface Technology, 2022, 51(7): 127-140.
责任编辑:刘世忠

