一种基于LSTM神经网络的荧光寿命还原算法

杨碧玉，徐跃，2

（1 南京邮电大学 集成电路科学与工程学院，南京 210023）

（2 射频集成与微组装技术国家地方联合工程实验室，南京 210023）

0 引言

荧光寿命成像技术（Fluorescence Lifetime Imaging Microscopy，FLIM）因其可获取用于提取生命系统潜在结构和功能变化的生物学数据而广泛应用于生物医学、化学分析、生命科学、细胞生物学等领域［1-5］，如癌症诊断［6-7］、皮肤病诊断［8］、脑组织分析［9］、药物动力分析［10-11］等。荧光寿命是荧光分子团的固有特性，对分子所处的微环境极其敏感［12］，因此，利用荧光寿命成像可以有效地研究蛋白间相互作用机理［13］、药物疗效［14］、生物组织微环境变化等。

荧光寿命成像质量强烈依赖于荧光寿命测量技术与荧光寿命还原算法。目前，基于时间相关单光子计数（Time Correlated Single Photon Counting，TCSPC）技术的时域测量方法因准确度高、易于弱光检测而成为生物研究领域中主流的荧光寿命测量方法［15］。TCSPC 法所得测量结果为荧光光子随时间的分布曲线，通过曲线拟合或其他形式的数据分析进行寿命还原可得到样品的荧光寿命值。传统的基于TCSPC 技术的荧光寿命还原算法主要有质心法（Center-of-Mass Method，CMM）与最小二乘法（Least Squares Method，LSM）。CMM 具有精度高、计算简单的特点［16］，但在估算长荧光寿命时精度明显下降，而LSM 通常需要提供适当的初始条件才能获得高的预测精度［17-18］。目前CMM 与LSM 主要用于荧光寿命在10 ns 范围内生物分子的荧光寿命还原，还不适用于快速、高精度、长荧光寿命的提取。近年来，新兴的深度学习技术也逐渐用于荧光寿命还原［19-21］。WU Gang 等［18］提出了一种基于人工神经网络（Artificial Neural Network，ANN）的高速FLIM 分析方法，其生成寿命图像的速度是传统LSM 的180 倍。SMITH J T 等［20］提出了一种荧光寿命成像网络（Fluorescence Lifetime Imaging Network，FLI-net），提供快速与无参数的处理，实现细胞中复杂荧光寿命的快速准确量化。XIAO Dong 等［21］提出了量化卷积神经网络（Quantized Convolutional Neural Network，QCNN）算法进行荧光寿命的还原，该算法在光子数为300～500 的情况下优于CMM 在光子数为9 000～10 000 时的还原精度。以上研究主要利用深度学习方法实现荧光寿命在10 ns 范围内的快速低光子FLIM 图像，但未涉及长荧光寿命还原问题。长荧光寿命物质大多为量子点，其荧光寿命范围为20～80 ns［22］，而广泛用于生物医学分子成像的荧光纳米探针的荧光寿命可达90 ns，因此目前迫切需要研究一种新的荧光寿命还原算法来解决宽荧光寿命范围内的还原精度、速度等方面的制约问题。

为了解决大动态荧光寿命还原精度低的问题，本文提出了一种基于长短时记忆（Long Short-term Memory，LSTM）神经网络的荧光寿命还原算法。该方法利用LSTM 神经网络对时间序列的强大学习能力进行荧光寿命还原，通过选取合适的超参数进行模型的搭建、训练与测试，并用蒙特卡罗仿真验证所提出方法在大动态范围内进行高精度、快速FLIM 成像的有效性。

1 LSTM 荧光寿命还原算法

当样品受到入射脉冲激光照射后，荧光分子团中处于激发态的电子发射一个光子后回到基态，从而产生荧光［16］，其发光强度随时间呈现指数衰减趋势，如图1（a）所示，荧光强度衰减至最大值的1/e 所消耗的时间定义为荧光寿命。为了准确检测荧光寿命通常将探测范围分为多个时间窗口，对于单个窗口每探测到一个光子则在其对应的计数器加一，将单个时间窗口的光子计数累加，记录多个周期后得到光子计数随时间变化的直方图，图1（b）展示了TCSPC 技术的原理。

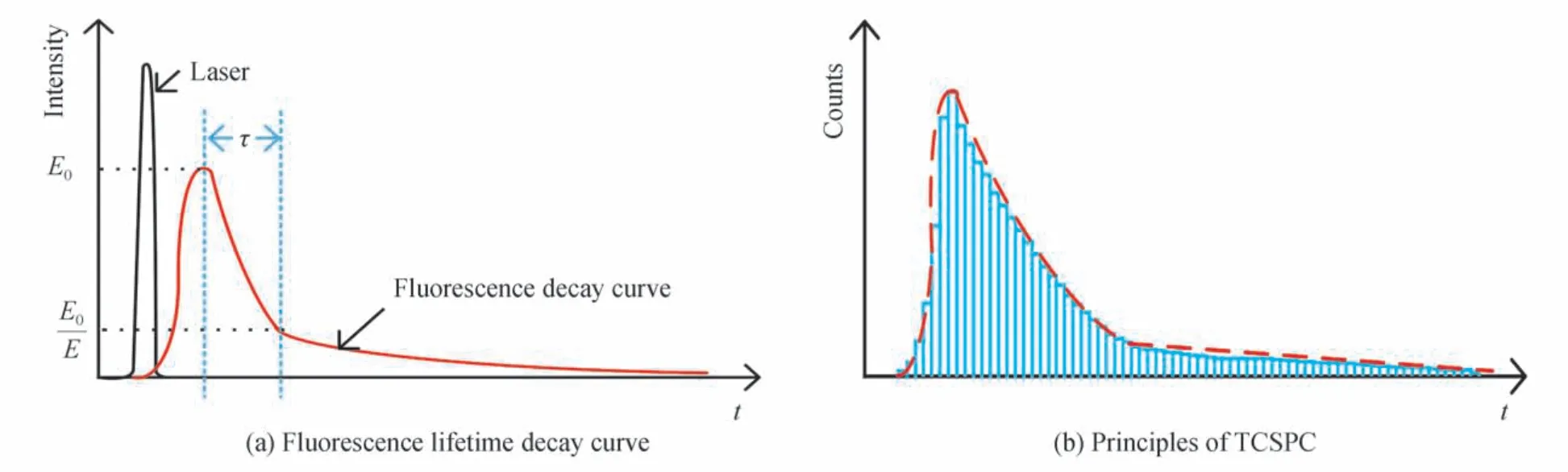
图1 TCSPC 法荧光寿命探测Fig.1 TCSPC method for fluorescence lifetime detection

TCSPC 进行荧光寿命探测所得到的直方图数据代表荧光衰减信号的时序序列，通过对时序序列进行数据分析处理可得到样品的荧光寿命值。选择搭建神经网络的方式对直方图衰减数据进行分析，通过模型的训练学习获得大动态范围内荧光寿命的衰减信息，主要分为网络模型结构的搭建与模型的训练调优两个阶段。网络模型结构包含输入层、隐藏层、输出层。其中，输入层用于重构荧光寿命直方图所得的时间序列数据，隐藏层主要用于学习直方图输入数据的特征与输出特征之间的映射关系，而输出层则进行反归一化处理并输出最终荧光寿命还原结果。图2展示了LSTM 荧光寿命还原网络模型的构建流程。首先，通过TCSPC 法生成多组时间序列数据，将这些数据分为训练集与测试集，其中训练集用于模型的训练，而测试集进行模型的测试。然后，在输入层上进行训练集与测试集数据的重构，将所有输入数据进行归一化处理后送入含有多层LSTM 网络的隐藏层，通过隐藏层提取出序列的时间相关性后再送入输出层。最后，将输出结果与理论结果进行比较计算得到模型的误差，然后使用优化器进行网络权值的更新，依次迭代后权重收敛，获得损失函数值最小的模型。最后输出层对隐藏层的输出结果进行反归一化处理，获得荧光寿命的还原值。

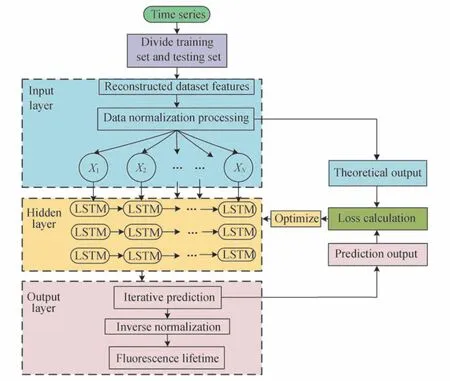
图2 LSTM 神经网络模型的构建流程Fig.2 Flow chart of the construction of the LSTM neural network model

应当注意到，在搭建的荧光寿命还原网络中隐藏层是一个重要的核心层，它一般包含多层LSTM 网络，而每层网络中又包含多个LSTM 神经元，用于对时间序列进行特征提取。一定数量LSTM 神经元组成如图3所示的链式结构，其中A 表示LSTM 神经元。每个LSTM 神经元包含一个用来保存长期记忆的细胞状态和输入门、遗忘门以及输出门。图3中输入门通过σ函数与tanh 函数对输入时间序列做处理，遗忘门通过σ函数对输入时间序列做筛选，输出门通过对当前记忆细胞Ct中的信息进行过滤输出，得到当前时刻的输出值ht作为近期信息，并与保持长期信息的Ct一起传递给下一个细胞，最终LSTM 神经元细胞通过三种门结构实现时间序列信息的保护与控制。

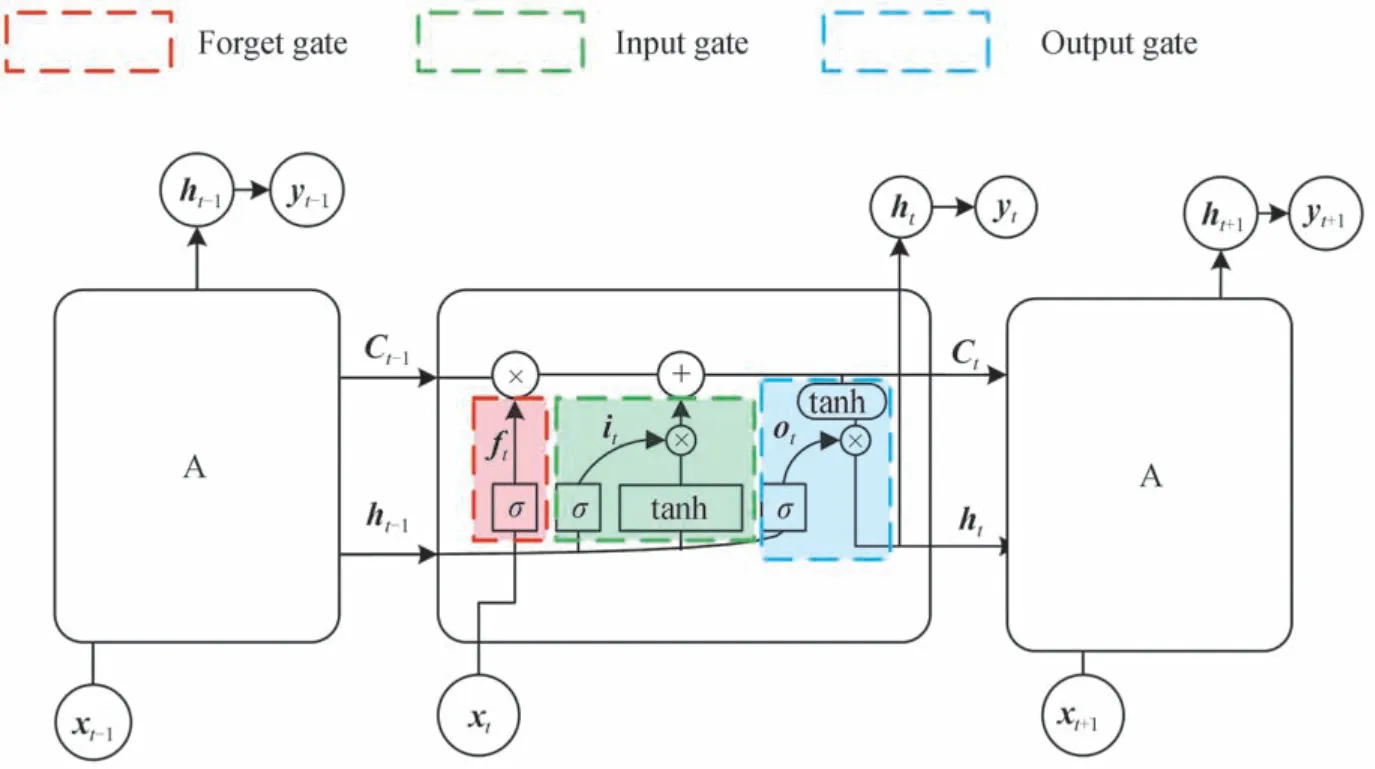
图3 LSTM 结构Fig.3 Structure of LSTM

对于给定的荧光寿命衰减时间序列xt，LSTM 神经网络计算公式可表示为［23］

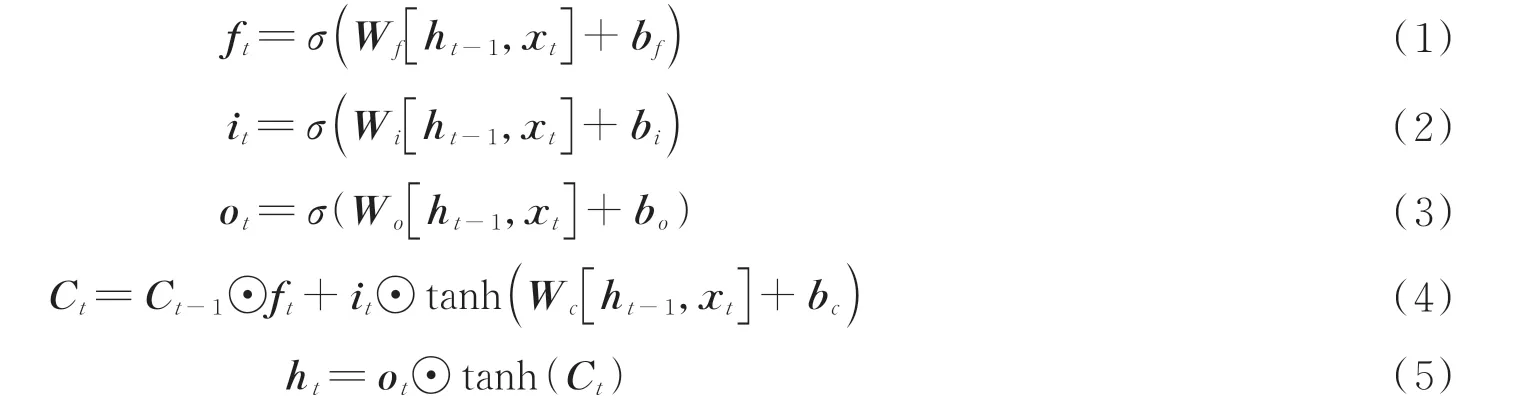
式中，ft、it、ot分别为t时刻遗忘门、输入门和输出门的状态，ht为隐藏状态，Wf、Wi、Wo、Wc分别为遗忘门、输入门、输出门以及细胞状态的权重，bf、bi、bo、bc分别为遗忘门、输入门、输出门以及细胞状态的偏置，⊙表示矩阵中的每个元素对应相乘，［］表示两个向量相连接。

每个神经元细胞的输出用Yt表示，理论输出为，Wy为输出权重，by为输出偏置，定义t时刻损失函数值为Lt，Ymn、为矩阵m行n列的值，则一次训练的损失函数L为每一时刻损失值的累加。Yt、Lt、L可以分别表示为

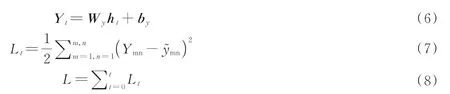
选择最小均方误差函数（Mean Squared Error，MSE）作为损失函数，用于对荧光寿命还原结果进行评价，其表达式为

式中，yi表示第i个样本的实际值，表示模型的预测值。MSE 越小，表明神经网络和训练集拟合性越好，匹配度越高。

为了提高LSTM 荧光寿命还原算法的准确性，需要对模型的超参数进行选取，包括LSTM 层数及每层神经元个数。参数的确定采用网格搜索方法进行，本质为穷举法。通过循环遍历所列出的超参数值域，使用每组超参数训练模型并挑选误差最小的超参数组合作为最终结果。网格搜索适用于超参数较少的情况，由于本文模型所需确定的超参数仅有2个，因此采用网格搜索方法，最终结果以1～100 ns 的荧光寿命进行预测的精确度为评价标准。为了避免模型预测的偶然性偏差，每种荧光寿命进行100 次测量取平均值τa作为其荧光寿命还原值，定义Δτ为荧光寿命还原值与理想荧光寿命值之间的偏差，则还原准确度可计算为

对LSTM 层数为1～4 层的神经网络进行训练，神经元固定为128 个，训练所需数据集由计算机生成，利用TCSPC 技术生成100 ns 范围内的20 000 个荧光衰减直方图，由直方图生成时间序列并储存为csv 文件格式，其中70%作为训练集数据，30%作为测试集数据，数据集中不同荧光寿命值均匀分布，计算机随机选取训练集与测试集。在隐藏层的LSTM 层间加入激活层与Dropout 层来防止训练模型过拟合，Dropout 层按1%的概率忽略直方图数据对应特征向量中部分位置的特征值，减少冗余权值，增加各个特征之间的正交性，最后加上全连接层汇聚所提取到的特征，对结果进行降维，得到如图4所示的结果。可以发现4 个模型的准确度均在94%以上，层数为3 的网络模型预测平均精确度更高，因此3 层LSTM 神经网络为最优。固定3 层网络层数，对每层的神经元个数分别设为16、32、64、128，进行模型训练与测试，图5显示了不同神经元个数下所训练模型在100 ns 内荧光寿命还原的效果。可以看到当神经元个数为128 时，所测结果的平均精确度更高。

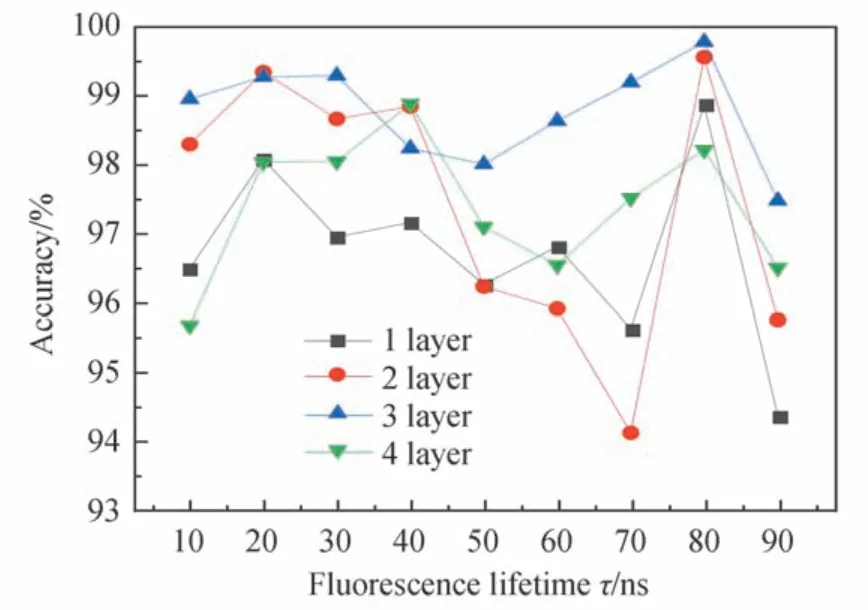
图4 相同神经元个数、不同层数时的测试结果Fig.4 Test results of the same neurons with the different layers

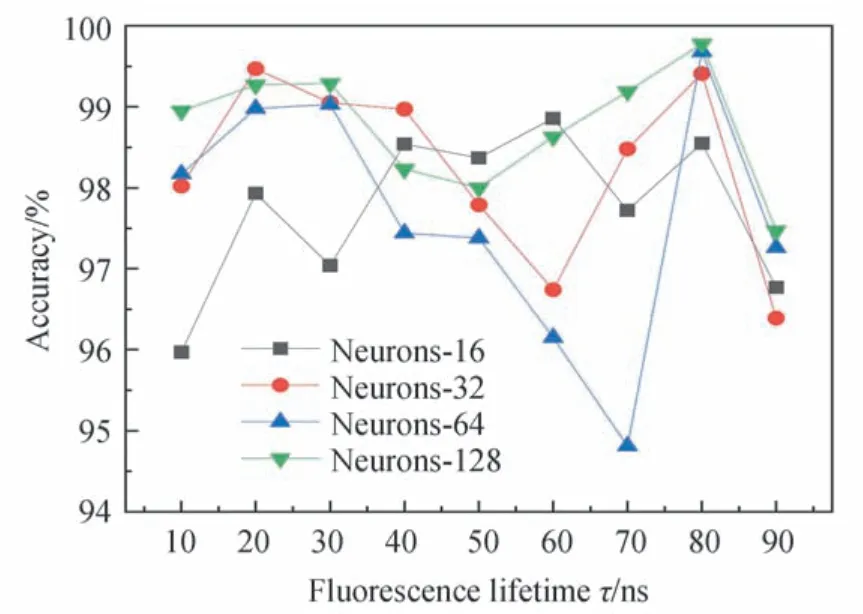
图5 相同层数、不同神经元个数时的测试结果Fig.5 Test results of the different neurons with the same layers

测试结果表明隐藏层包含3 层LSTM 网络，每层包含128 个神经元的网络结构更适用于荧光寿命还原，图6为所选网络结构，其中激活层的激活函数为双曲正切S 型函数，层间使用Dropout 层丢弃部分信息，最后使用全连接层汇聚荧光寿命衰减信息。

图6 网络结构Fig.6 The structure of the network

2 荧光寿命还原仿真

仿真实验采用Tensorflow2.7 深度学习框架，使用Python 语言编程实现，仿真运行环境为JetBrains PyCharm Professional Edition 软件，操作系统为Windows11（64 位），内存为16 GB，处理器为Intel（R）Core（TM）i5-1157 G7 2.50 GHz。在该实验环境下采用蒙特卡罗法进行单点的荧光寿命还原仿真，该方法以概率为基础，以抽样为手段对单个个体进行行为仿真并建立概率模型或随机过程［24］，即以理想荧光寿命值为参数生成一组服从指数分布的随机数，每个随机数代表一个光子，将光子累计放入相应时间窗口。仿真中荧光寿命探测周期设置为100 ns，时间窗口数M设置为1 000，每个窗口的长度设为100 ps，Nj为第j个窗口检测到的光子。Nc是在整个曝光期间检测到的光子总数，设置为1 000。荧光光子到达探测器是一个服从泊松分布的计数过程，光子探测引发的光子计数噪声是一种与荧光信号相关的泊松型噪声。在不忽略泊松噪声的情况下Nj的表达式为

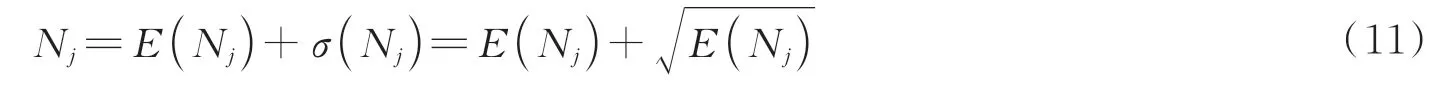
式中，Nj为单独的泊松分布，E（Nj）与σ（Nj）分别为泊松分布的平均值与标准差［25］。每个时间通道中添加的个光子即为泊松噪声。此时经过仿真可构建出时间窗口数为1 000 的光子数分布直方图，为减少神经网络的输入，将每10 个窗口对应数值进行合并使窗口数为100，图7（a）、（b）分别为光子计数值为1 000时，荧光寿命为10 ns 以及80 ns 条件下所生成的直方图。

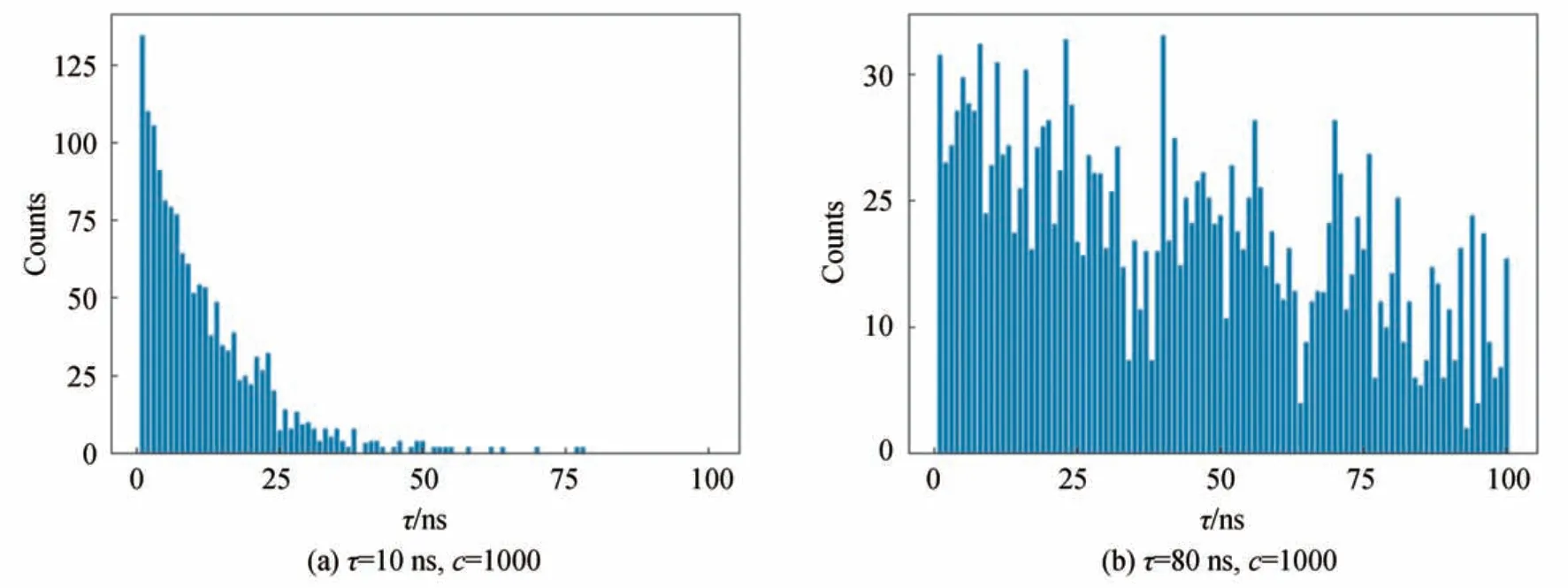
图7 荧光寿命衰减直方图Fig.7 Histogram of fluorescence lifetime decay

取出直方图中对应时间窗口的一组时间序列数据x，对数据按最小值中心化后，再按（最大值-最小值）进行缩放，使数据收敛至［0，1］之间，其目的是消除数据之间不同数量级的差异，避免数量级差异过大导致预测的准确度减小，同时也能加快网络学习与训练过程的收敛性。

将归一化处理后的数据作为模型的输入送入第二节训练好的荧光寿命还原模型中，其反归一化计算结果为单点荧光寿命的还原值。当对阵列进行还原成像时，需对阵列中每个点进行还原，得到所有点的荧光寿命还原值后再使用伪彩色进行阵列成像。图8（a）为初始荧光寿命成像图，包含8 种荧光寿命值，分别为10 ns、11 ns、12 ns、14 ns、16 ns、18 ns、22 ns 以及26 ns。图8（b）为使用LSTM 还原算法对8 种荧光寿命还原后成像的结果，可见LSTM 还原算法对10～30 ns 内所选取的8 种荧光寿命能进行较好的还原。

图8 32×32 阵列还原结果Fig.8 The restoration results of 32×32 array

3 结果与讨论

为了验证所提出的LSTM 荧光寿命还原算法的优点，将其与同样基于TCSPC 技术的CMM、LSM 算法进行性能对比。对相同荧光寿命利用蒙特卡罗法及TCSPC 技术模拟生成100 组数据后加入泊松噪声，比较了在寿命范围90 ns 情况下，光子计数分别为5 000 与10 000 时3 种荧光寿命还原算法的准确度和标准差。

利用三种算法在光子数为10 000 时，对荧光寿命1～90 ns 内每隔5 ns 荧光寿命所生成的直方图进行寿命还原，结果如图9所示。图中横坐标为理想荧光寿命值，纵坐标为还原值。可以明显地发现CMM 在荧光寿命值超过20 ns 后还原效果急剧恶化，LSM 相比于LSTM 算法的还原值与理想寿命值偏差更大，而LSTM 算法可在90 ns 的大动态范围内实现荧光寿命准确还原，其还原范围是CMM 算法的4.5 倍，同时拥有比LSM 更高的还原精度。

图9 CMM、LSM 与LSTM 还原范围对比Fig.9 Comparison of CMM，LSM and LSTM retrieval range

在光子计数为5 000 时对长短荧光寿命分别选取多个寿命值进行单点还原来实现三种算法性能的定量比较，对于短荧光寿命，选取5 ns 和10 ns 两种荧光寿命值，对于长荧光寿命，选取40 ns、80 ns 以及90 ns 的荧光寿命值。为了避免偶然性误差，对相同理论寿命采用三种算法进行100 次还原后取平均值作为其还原寿命值，结果如表1所示。对于短荧光寿命还原，三种算法准确度均大于90%；对于长荧光寿命，CMM 难以进行准确还原，与LSM 相比，LSTM 算法拥有更低的还原标准差和更高的还原准确度。

表1 光子计数为5 000 时CMM、LSM 与LSTM 算法单点还原对比Table 1 Comparison of CMM、LSM and LSTM algorithms for retrieving single point when the photon count is 5 000

在光子计数为10 000 时重复上述实验进行荧光寿命的还原，结果如表2所示。对于短荧光寿命还原，三种算法的准确度受光子数的影响较小；对于长荧光寿命，CMM 依旧难以进行准确还原，与光子数为5 000 相比，LSM 算法与LSTM 算法对荧光寿命的还原准确度均有所上升且标准差减小。

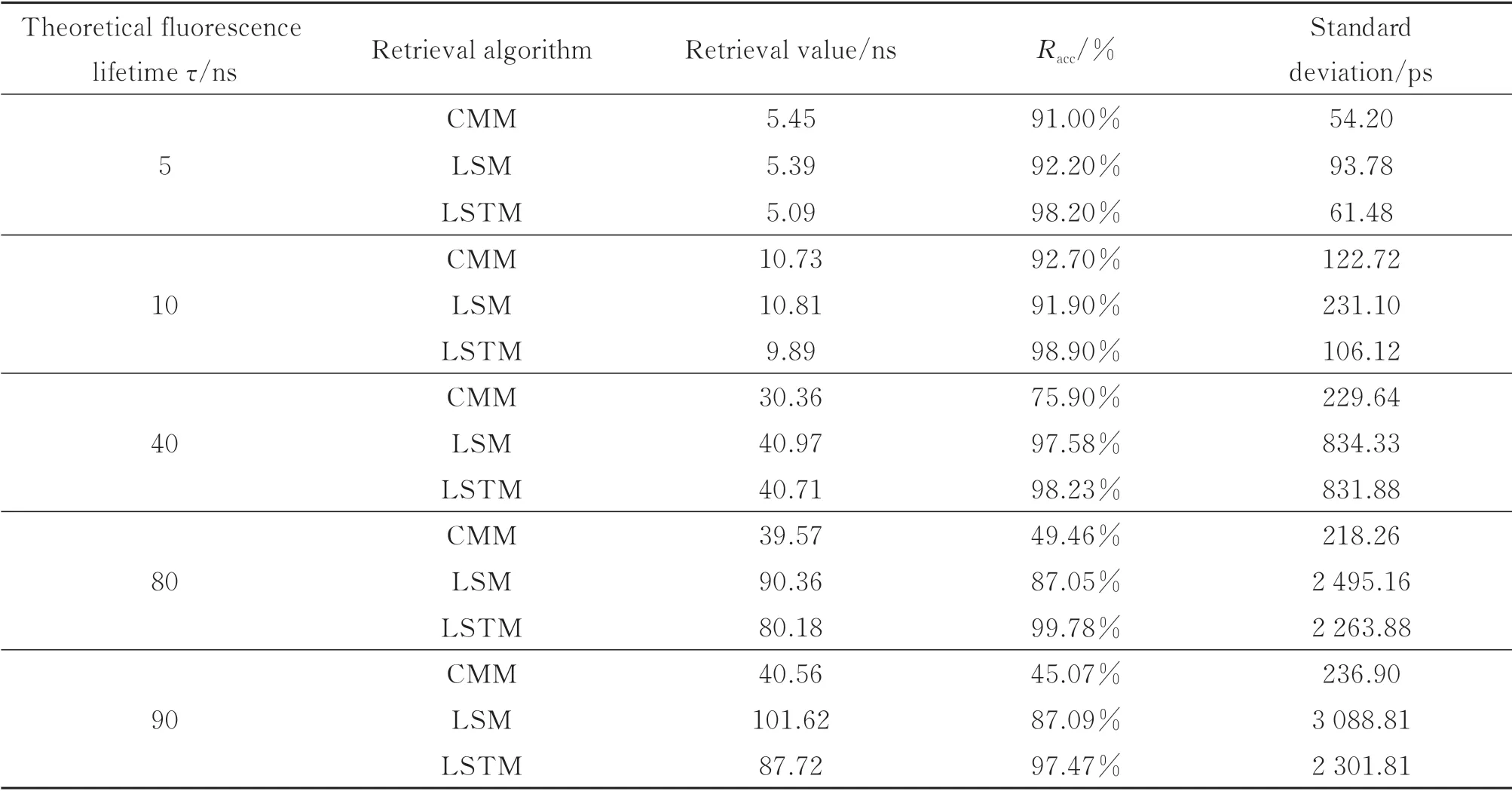
表2 光子计数为10 000 时CMM、LSM 与LSTM 算法单点还原对比Table 2 Comparison of CMM、LSM and LSTM algorithms for retrieving single point when the photon count is 10 000

从单点还原结果可见CMM 更适用于短寿命还原，而LSM 需将拟合阶次与窗口宽度结合，参与拟合的窗口宽度必须大于拟合阶次，因此需要人工选取适合的拟合窗口宽度，光子数较少的情况下其拟合结果与本文所提方法相比精确度略低，标准差略高。

应当注意到单点还原的结果因为泊松噪声的存在成为一个随机过程，因此需要进一步利用阵列的方式来进行荧光寿命还原成像效果的仿真与分析。预先设定好32×32 阵列中每个像素所对应的初始荧光寿命值，然后对所有像素分别使用CMM、LSM 与LSTM 算法进行荧光寿命还原，对于短寿命范围的还原，阵列中选取5 ns、10 ns、15 ns 三种荧光寿命值进行成像，图10显示了3 种还原算法的阵列成像结果。在荧光寿命为短寿命时，CMM、LSM、LSTM 均能很好地进行荧光寿命成像。此外，在阵列中选取40 ns、60 ns、80 ns 较长的荧光寿命值进行阵列成像，还原结果如图11所示。可见，CMM 对于长寿命难以准确成像，而LSM 和LSTM 对于长寿命均可进行还原成像，但相比之下LSTM 算法的成像效果更优。对于32×32 阵列的成像，经过多次实验计算表明，CMM 可在0.07 s 完成计算，LSM 需要大约77 s，而LSTM 算法使用多进程编程时大约需要9.7 s。当提升硬件条件时，该算法将会在更短的时间内完成阵列还原，为实时成像提供了可能。

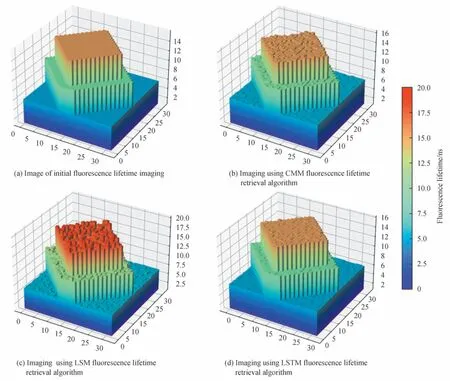
图10 τ1=5 ns，τ2=10 ns，τ3=15 ns 时阵列成像效果对比Fig.10 The comparison of array imaging when τ1=5 ns，τ2=10 ns，τ3=15 ns

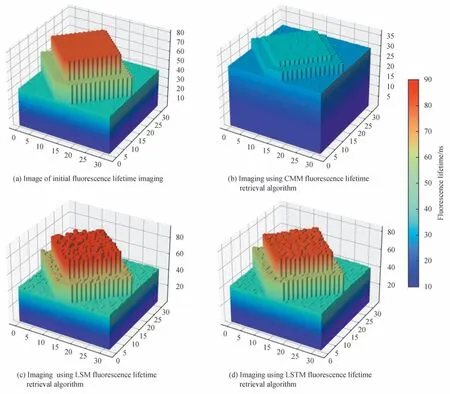
图11 τ1=40 ns，τ2=60 ns，τ3=80 ns 时阵列成像效果对比Fig.11 The comparison of array imaging when τ1=40 ns，τ2=60 ns，τ3=80 ns

4 结论

本文提出了一种基于LSTM 神经网络的荧光寿命还原算法，实现了90 ns 范围内的荧光寿命还原。采用深度学习技术提取TCSPC 技术所生成直方图中的时域信息，建立直方图与荧光寿命的对应关系并进行模型训练。蒙特卡罗模拟仿真表明本文所提出的LSTM 算法与同样基于TCSPC 的CMM 相比，其还原范围由20 ns 拓宽至90 ns，与LSM 相比，LSTM 算法的精确度平均可提高5%，对于32×32 阵列的成像速度提升约8 倍。该LSTM 荧光寿命还原算法在保证还原精确度的情况下能显著拓宽荧光寿命还原范围，适用于单指数大动态范围荧光寿命的精确还原成像。