一种CMG框架伺服系统的改进自抗扰控制策略

赵文鹏 刘 昆

中山大学航空航天学院，广州 510006

0 引 言

控制力矩陀螺(CMG-Control Moment Gyro)是航天器姿态控制的一类执行机构，对航天器姿态控制和保持航天器长期稳定运行起到关键作用。CMG以其机械结构简单、输出力矩大等优点被广泛应用到航天器上，“天宫一号”和“天宫二号”即选用了CMG作为执行机构[1-2]。

CMG由高速转子系统和框架伺服系统组成，框架伺服系统的控制精度影响整个CMG系统的输出力矩精度。CMG框架伺服电机的转速一般很低，系统中存在的转矩扰动严重影响了其控制精度[3-4]。当框架电机驱动框架低速运转时, 沿框架轴方向主要会受到3种干扰力矩：摩擦力矩、阻尼力矩、以及高速转子动不平衡引起的高频干扰力矩。相关学者对CMG伺服系统的控制算法做出了很多研究。文献[5]通过建立干扰力矩观测器抑制了摩擦力矩等干扰力矩的影响，但抑制效果比较有限。文献[6]和文献[7]设计了自适应滑模控制器来抑制干扰力矩，在一般转速下系统工作性能得到了一定的提升，但在低转速范围内控制效果并不明显。文献[8]通过自抗扰控制(ADRC-Auto Disturbance Rejection Control)有效抑制了系统中干扰力矩的影响，在1rad/s的转速设定下具有较好的仿真效果，同时提高了系统的稳态精度。传统的ADRC是非线性的，并且存在较多待整定的参数，在控制器设计上存在较大困难，不便于工程应用[9]。为了减少ADRC的整定参数，简化控制器设计，高志强提出了线性自抗扰控制器(LADRC-Linear Auto Disturbance Rejection Control)，引入了频域中带宽的概念，将控制器的设计参数与控制器带宽联系起来，给出了LADRC的参数整定公式，对于实际的工程应用具有重要的意义[10]。

在CMG框架伺服系统的干扰力矩中，由动不平衡引起的高频干扰力矩的幅值与高速转子转速的平方成正比，频率与高速转子转速同频，是一种大幅值高频干扰力矩，对CMG框架控制精度带来了较大影响。相关文献[11]指出，传统的扩张状态观测器对于常值外界扰动能够实现渐近跟踪，对于CMG框架伺服系统中存在的周期性扰动无法完全估计，从而产生转速波动。

针对以上问题，本文建立了CMG框架伺服系统的数学模型，针对转速环设计了LADRC控制器，并利用CMG框架伺服系统中存在的由高速转子动不平衡引起的周期性扰动的先验信息，改进扩张状态观测器结构，适当增加扩张状态观测器阶数来提高系统跟踪性能。仿真结果表明，改进的LADRC对于周期性扰动抑制效果显著，提高了CMG框架伺服系统的低速控制精度。

1 CMG框架伺服系统建模及扰动分析

1.1 CMG框架伺服系统建模

CMG框架电机通常采用永磁同步电机(PMSM)，而永磁同步电机具有非线性、多变量、强耦合的特点，在建立数学模型前，通常做如下假设[12]：

1)转子永磁磁场在空间的分布与定子电枢绕组中感应电动势严格按正弦规律变化；

2)永磁体材料电导率为0，永磁体内部磁导率与空气相同；

3)忽略定、转子铁芯磁阻，不计磁滞损耗和涡流损耗的影响；

4)定子绕组三相严格对称分布；

5)转子上无阻尼绕组。

根据以上假设，采用id=0的矢量控制，可以建立两相旋转坐标系(dq坐标系)下的PMSM数学模型，如下所示：

电磁转矩方程：

Te=1.5npψfiq

(1)

运动方程：

(2)

d/q轴电流方程：

(3)

式(1)～(3)中，相关变量含义如表1所示。

表1 PMSM数学模型参数

矢量控制原理如图1所示，采用了电流内环和转速外环的双闭环控制[13]。

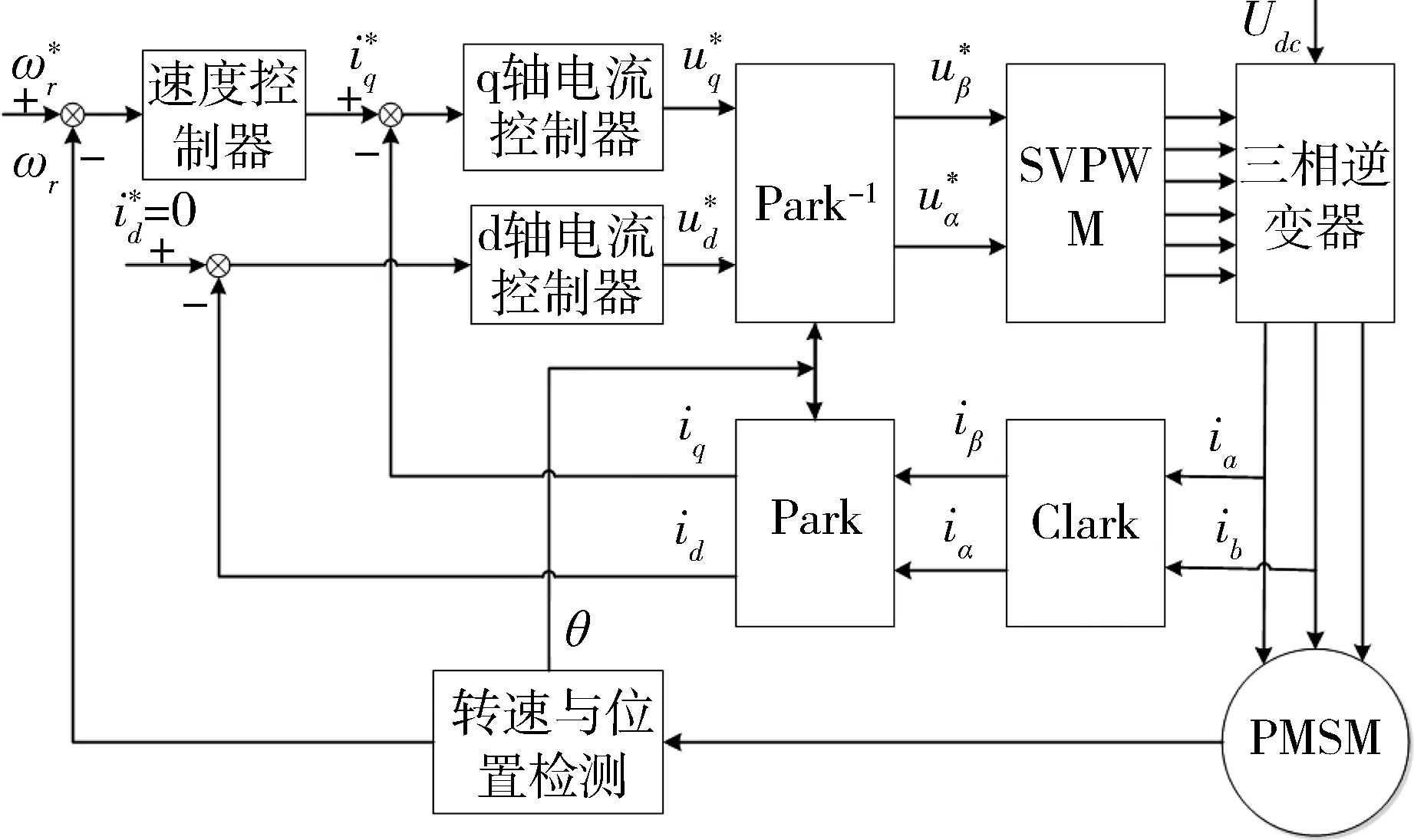
图1 矢量控制原理框图

1.2 CMG框架伺服系统扰动分析

CMG框架伺服系统的扰动包括了摩擦力矩，阻尼力矩，齿槽效应和磁通畸变引起的脉动力矩以及转子动不平衡引起的高频扰动力矩。其中齿槽效应和磁通畸变引起的脉动力矩可通过电机优化设计和磁通补偿的方式改善。摩擦力矩造成框架伺服系统产生低速爬行以及极限环振荡等，可通过分析摩擦产生的机理，建立摩擦力模型进行前馈补偿解决[14]。

由于制造工艺等原因，陀螺房内的高速转子质量分布并不完全均匀，其在高速旋转时会产生一个偶不平衡力矩，使得高速转子的旋转主轴相交于质心，但与其几何中心不重合，会在如图2所示沿框架轴xg方向上产生一个力矩分量，从而对框架施加扰动力矩，严重影响了CMG框架伺服系统的控制精度[15]。相关学者发现CMG中偶不平衡力矩沿框架轴方向的力矩分量为[16]

T0=-JrΩ2ArsinΩt

(4)

式中,Jr为高速转子的转动惯量；Ar为一个常系数；Ω为高速转子的角速度。

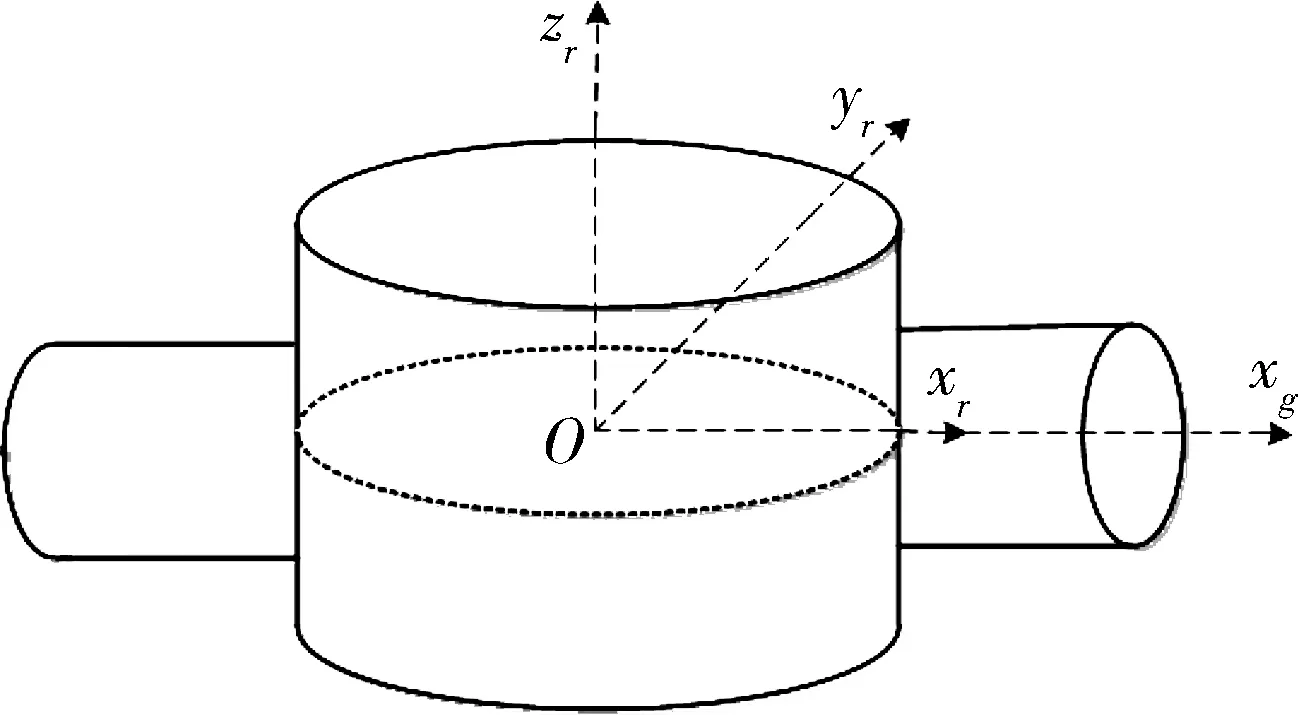
图2 CMG坐标系

CMG框架电机运行转速很低，而转子动不平衡引起的扰动为大幅值高频扰动，频率远超CMG框架伺服系统的带宽，常规的控制器控制效果不佳。在框架伺服系统运行时，高速转子稳态运行，转速基本不变，根据式(4)，动不平衡引起的干扰频率也基本不变。因此，本文根据转子动不平衡引起固定频率扰动的模态信息，对LESO重新进行设计。

2 LADRC原理

传统的ADRC由跟踪微分器、扩张状态观测器和非线性误差反馈控制律三部分组成。跟踪微分器通过安排过渡过程，解决了传统PID控制器响应速度和超调之间的矛盾。扩张状态观测器将系统未建模部分和未知扰动归结为“总扰动”，替代误差积分反馈作用，不仅能够抑制常值干扰，对于一些随机干扰也能有很好的抑制效果[17]。ADRC并不依赖于被控对象的数学模型，只需要知道被控对象的阶数和系统输入矩阵的大概数值即可。但是因为控制器设计复杂，参数整定无实际物理意义上的指导，所以传统的ADRC难以应用于工程实际中。由于转速作为系统最终输出，大部分扰动都发生在转速环中，为便于工程应用，只将转速控制算法改为LADRC，电流环保留原PI控制。

线性跟踪微分器(LTD)：

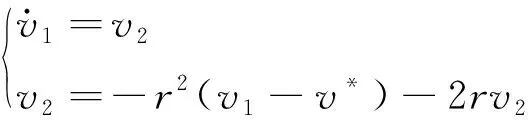
(5)

式中,v*为给定值；v1为v*的跟踪信号；v2为v1的微分信号；r为跟踪微分器的跟踪快慢因子，r越大，跟踪速度越快，但是r过大也会导致系统出现超调。

线性扩张状态观测器(LESO)：

(6)

式中，y为输出值；z1为y的观测值；e为观测误差；z2为扩张扰动的估计值；β1和β2为状态反馈的增益系数，增益越大，观测器对输出和扰动跟踪能力越强。

线性误差反馈控制律(LSEF)：

u=k1(v1-z1)-z2/b

(7)

式中，k1为反馈控制系数， LADRC速度控制原理框图如图3所示。

图3 LADRC原理框图

3 改进LADRC的PMSM速度控制器设计

在PMSM系统中，速度环控制器选用一阶的LADRC，根据式(1)～(2)选择状态量为[x1,x2]T=[ωr,-(TL+Tf+Dωr)/J]，输入量u=iq。得到状态方程为

(8)

根据(6)式得到LESO的矩阵形式

(9)

则根据式(8)～(9)可以得到误差状态方程

(10)

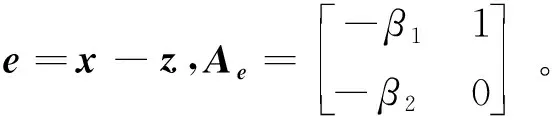
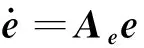
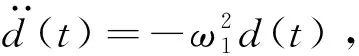
(11)

根据式(11)可对系统状态进行重构，则

(12)

根据重构后的系统设计LESO如下

(13)

根据式(13)可知LESO的特征方程为

(14)

通过带宽法来整定LESO的增益系数，由式(14)可得整定公式为

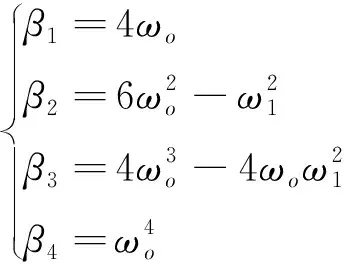
(15)

式中，ωo为LESO的带宽。

4 改进LADRC的稳定性证明

根据式(12)((13)可得到状态重构后的LESO误差方程

(16)

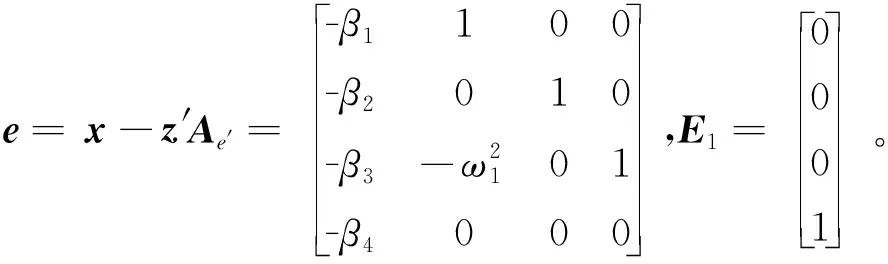
为了使观测误差趋近于0，矩阵Ae′必须具有Hurwitz性，即保证特征方程|sI-Ae′|的特征根具有负实部，利用观测器带宽的概念可选取特征方程为：

(17)

(18)

则特征方程为

(19)

根据式(16)、(18)和(19)可以得到

(20)

(21)

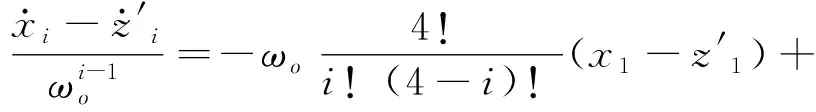
(22)

(23)

现令

(24)

(25)

则式(22)和(23)合写为

(26)

在式(26)中假设右边只有第1项，则根据式(25)一定能保证A2的Hurwitz性[18]，即保证观测器观测误差渐近趋近于0。而第二项的h1为扩张状态不含周期性干扰项x22的微分量，是误差的有界函数，系统达到稳态时，可认为h1=0，则证得

(27)

5 仿真校验

本次设计通过Simulink建立了基于LADRC的速度控制的CMG低速框架伺服系统模型，采用国防科技大学研制的磁悬浮控制力矩陀螺作为研究对象，其框架电机的参数如表2所示[19]。

表2 框架电机参数

设计线性跟踪微分器的快慢因子r=1000，控制力矩陀螺框架电机转速一般不超过3r/s，则控制器带宽要大于3Hz，为保留一定的裕度，综合选取控制器带宽ωc=150rad/s，得到控制器增益k1=150。根据工程经验，控制器带宽ωc与观测器带宽ωo的关系一般为ωo=3～5ωc，则选择LESO带宽ωo=500rad/s。假定陀螺房内高速转子保持稳态运行速度为Ω=10000r/min，则根据式(10)，假设动不平衡引起的扰动力矩为T0=sinΩt，则根据整定公式(15)可设计LESO增益系数。

本文通过比较传统的LADRC速度控制器与所设计的改进的LADRC速度控制器，研究高速转子动不平衡引起的扰动力矩对于CMG框架低速性能的影响以及系统性能的变化。分别设定转速给定值为0.1rad/s和1rad/s，图4～5显示了传统的LADRC在稳态时存在周期性变化的稳态误差和理论分析一致。传统的LADRC只能对常值扰动渐近收敛到0，无法抑制周期性变化的扰动。而改进的LADRC基本完全抑制了由转子动不平衡引起的周期性扰动。由图6可以看出传统的LADRC估计误差在上界为0.05rad/s，下界为-0.05rad/s的领域内周期性变化，而改进的LADRC估计误差在稳态时能够收敛到0。

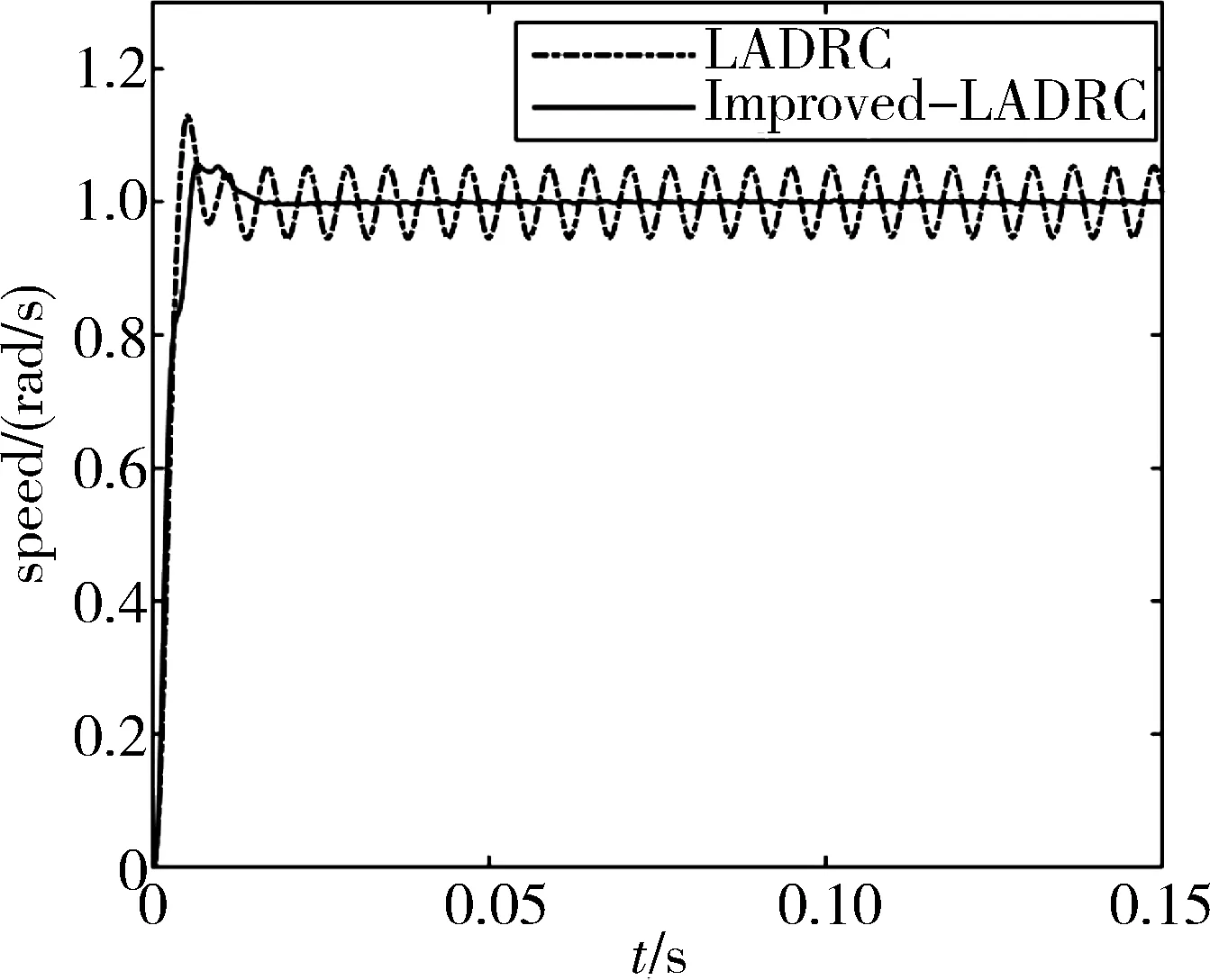
图4 1rad/s给定下转速阶跃响应曲线

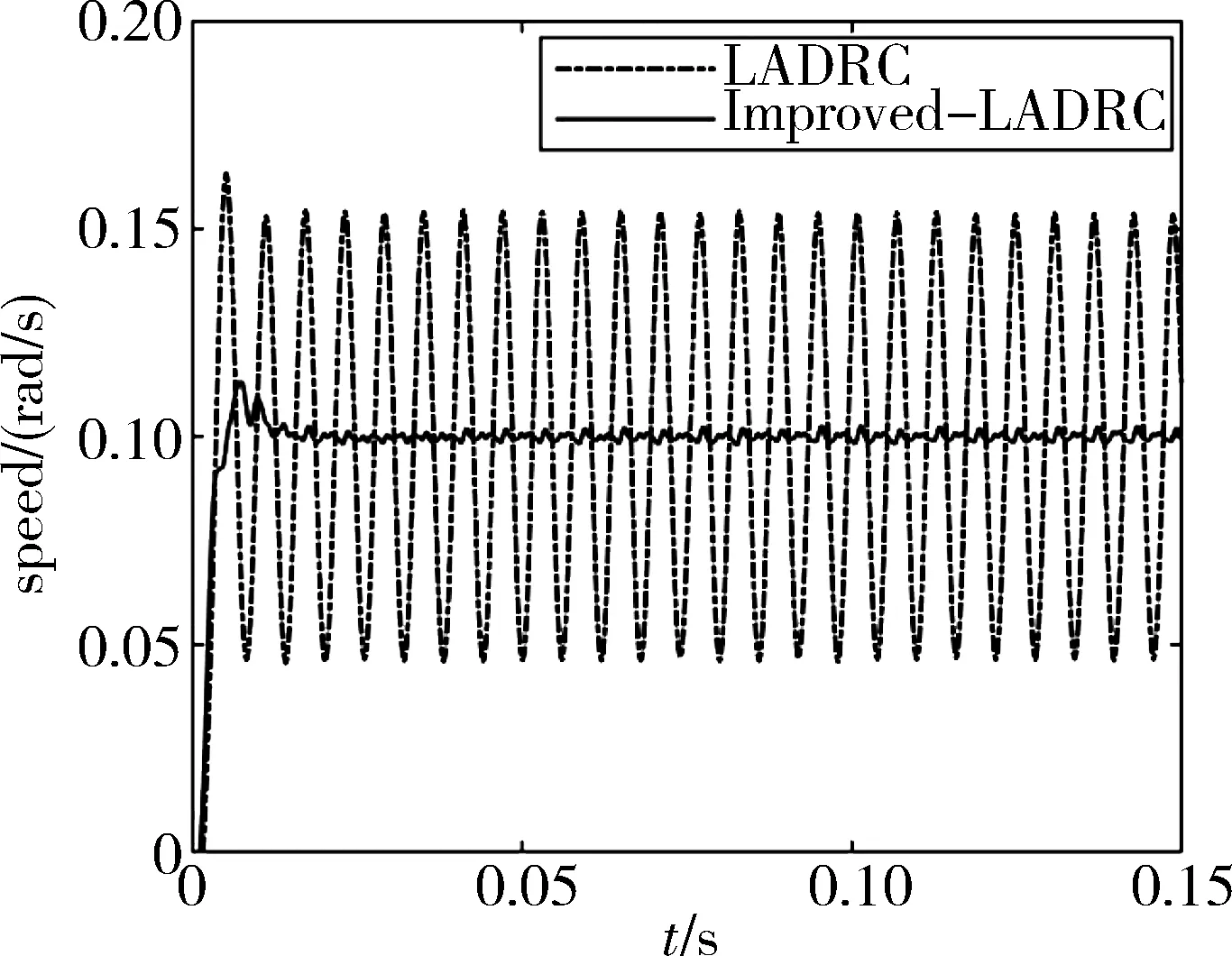
图5 0.1rad/s给定下转速阶跃响应曲线

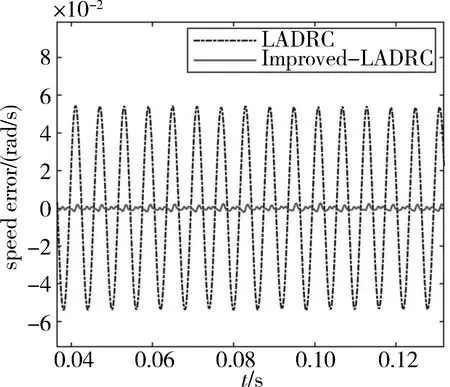
图6 转速阶跃响应下稳态误差曲线

航天器姿态控制系统给定的CMG框架伺服电机的参考速度指令带宽不高于3Hz，则设定转速给定值频率为3Hz，幅值为1rad/s的正弦给定指令。图7可以看出传统的LADRC速度周期性波动明显，由转子动不平衡引起的扰动力矩使得框架角速度以0.05rad/s幅度波动。相较而言，改进的LADRC下框架角速度几乎无波动，转速跟踪误差幅值约为0.02rad/s，相位滞后小于0.02rad。干扰抑制效果明显，转速控制性能得到改善。

图7 正弦给定指令下的转速响应曲线

除了CMG高速转子动不平衡引起的周期性扰动外，转换到dq坐标系后，系统一般还受到6次、12次以上的谐波干扰，为验证所设计控制系统对多源外界干扰的抑制效果，现同时加入CMG高速转子动不平衡引起的周期性干扰和6次、12次的谐波干扰，并在0.1s时突加1N·m的负载。图8可以看出在周期性干扰和谐波干扰的1rad/s给定下，改进的LADRC不仅对周期性干扰抑制效果明显，对于谐波干扰也有一定的抑制效果。在突加1N·m的负载后，改进的LADRC转速下降约0.025rad/s，即下降2.5%，由于所设计的改进LADRC与传统LADRC控制器带宽一致，调节时间约为0.03s，和传统LADRC相比基本不变。

图8 多源干扰下1rad/s的转速阶跃响应曲线

仿真结果表明，通过改进的LADRC速度控制解决了传统LADRC控制器受CMG高速转子动不平衡产生的周期性扰动力矩而引起的转速波动，稳态跟踪误差显著降低，系统跟踪性能得到进一步提升，对于多源外界干扰也有较好的抑制效果。

6 结论

针对传统LADRC难以抑制CMG转子动不平衡引起的周期性扰动的问题，将周期性扰动模态信息引入LESO进行状态重构，从而对这种周期性扰动实现估计与补偿。仿真结果表明，经过改进的LADRC基本消除了由CMG转子动不平衡引起的周期性扰动，同时对多源外界干扰也有较好的抑制性能，从而提高了速度跟踪精度，使系统低速控制精度进一步提高。