孔雀垂直起降飞行器数学仿真模型*

贾晨辉 骆无意 柳嘉润 吕新广 李新明 巩庆海 张 隽

北京航天自动控制研究所，宇航智能控制技术国家级重点实验室，北京 100854

0 引言

可重复使用运载火箭是近年来新兴的一项航天飞行控制技术。美国当地时间2015年12月21日晚，特斯拉公司创始人埃隆·马斯克创办的太空探索技术公司(以下简称SpaceX)发射的“猎鹰9”火箭在佛罗里达州卡纳维拉尔角成功实现第一节火箭软着陆，从而开创了火箭从太空直接垂直回收的历史[1]。近年来，火箭的垂直回收技术受到了国内外多个高校、研究机构的广泛关注，该技术不仅极大降低了火箭的发射成本，使火箭具备了可重复使用的能力，而且可以使火箭带回更多的飞行数据供研究人员参考、分析，为提升后续火箭的各项性能提供数据基础。

“孔雀”系列飞行器为一款可重复使用的垂直起降技术验证平台，可用于验证运载火箭垂直回收、非程序制导及智能飞行控制等各项关键技术[2]。。该飞行器目前已服役3年，参加了多次飞行验证试验，实现了多项关键技术的突破。

为支持航空航天飞行器的飞行控制研究，各研究机构建立了多种飞行器的数学模型供航空航天研究人员或爱好者进行控制仿真研究。如NASA公布了F-18 HARV战斗机数学模型[3]，以及一些学者公布了一系列超音速飞行器的数学模型[4-5]等。但由于运载火箭垂直回收技术研究刚刚起步，目前鲜有对外发布的可重复使用运载火箭数学模型供航天工作者进行运载火箭垂直回收等技术的控制仿真分析与研究工作。

本文建立孔雀飞行器的数学模型用于为垂直起降飞行器控制技术研究人员提供一套可进行控制仿真研究的被控对象模型，该数学模型根据孔雀飞行器的设计过程及飞行试验过程的参数建立，作为孔雀飞行试验前的数学仿真和半实物仿真依据，实现孔雀飞行器各项控制算法的验证，亦可作为可重复使用运载火箭飞行控制仿真研究的被控对象模型使用。

1 符号说明与基本假设

1.1 符号说明

孔雀飞行器模型的常用符号如表1所示。

1.2 基本假设

1)飞行器为刚体，忽略弹性振动；

2)平坦静止大地，忽略地球曲率和地球转动的影响；

3)忽略燃油消耗导致的转动惯量、惯性积、质心位置变化；

4)忽略发动机转子转动导致的陀螺效应；

5)忽略发动机摆动角加速度导致的附加力矩。

2 被控对象模型

2.1 孔雀飞行器外形

孔雀飞行器外形及主要舱段如图1所示。本文中所介绍的模型为不包含涵道风扇与栅格舵(仅计算二者重量)的飞行器模型。

表1 孔雀飞行器模型的常用符号

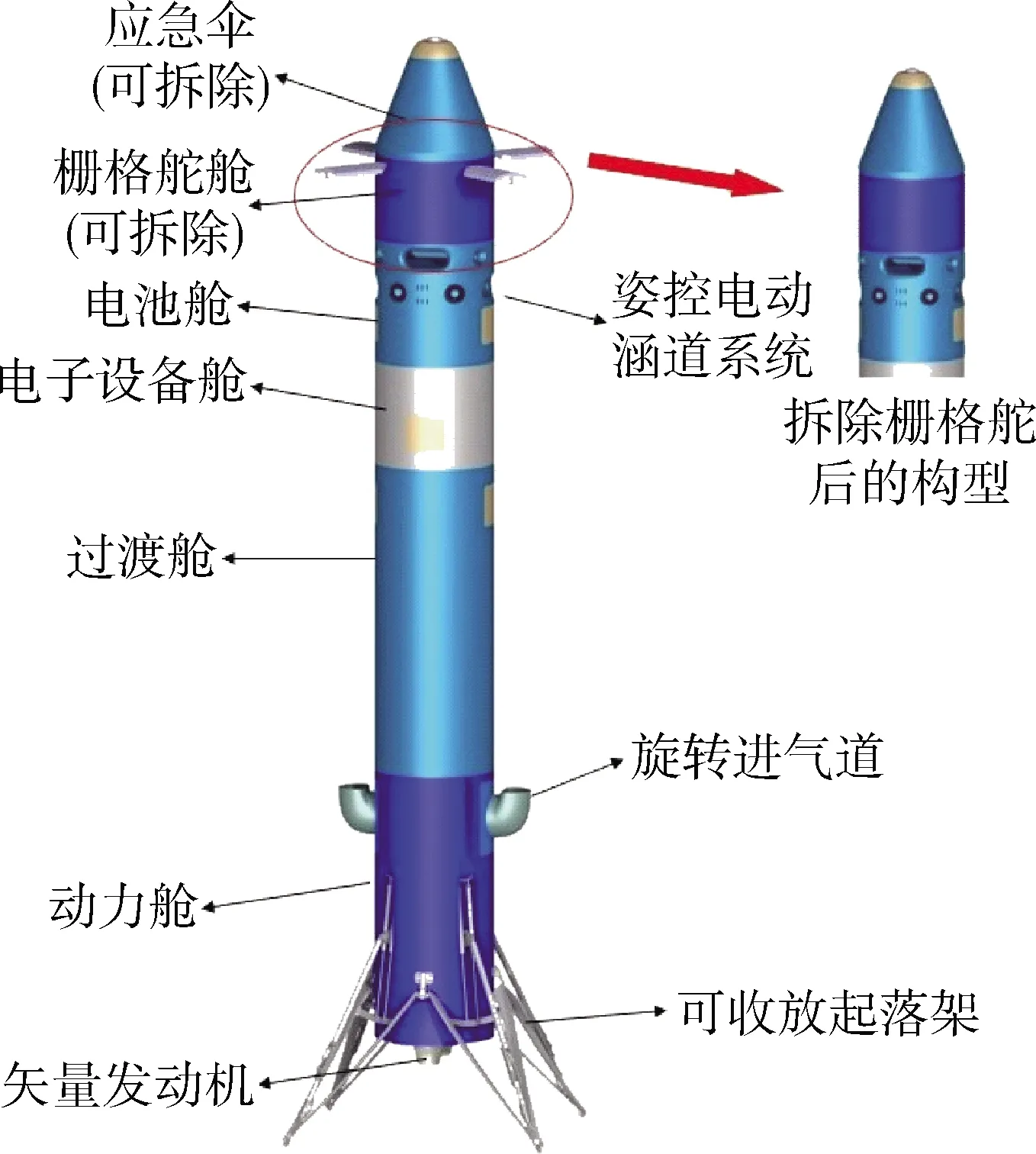
图1 孔雀飞行器外形图

2.2 坐标系

采用俄罗斯体制的“北-天-东”坐标系，定义符合右手定则的空间直角坐标系，其定义见参考文献[6]。

地面系与箭体系之间的关系可以用俯仰角φ、偏航角ψ和滚转角γ这3个姿态角来确定。姿态角按照从地面系到箭体系为3-2-1的转序定义。

2.3 被控对象模型

2.3.1 风模型

(1)

考虑飞行器处于水平定常风场中，即仅考虑水平方向的风。风向角θw定义为：按右手定则，从地面系OdXd轴开始，绕OdYd轴转动到风速矢量的角度。地面系下的风速按式(2)计算：

(2)

在一次仿真中风向角θw为常数。

风速大小vw设置为随高度变化的仿真量，其表达式为：

vw=kwindyvw1≤vw≤vw2

(3)

其中，kwind为风速相对于高度变化的比例系数；vw1，vw2为仿真中风速的上下限幅值。

(4)

2.3.2 飞行器运动方程

飞行器运动方程的状态为：地面系位置[x,y,z]T；地面系速度[vx,vy,vz]T；姿态角[φ,ψ,γ]T；箭体轴转动角速度[ωx,ωy,ωz]T；此外，发动机耗油导致质量变化。微分方程如式(4)所示，其中：

(5)

式中，Tt→d为箭体系到地面系的转换矩阵；[FA,FN,FZ]T为气动力在箭体系下的分量表示；[Pxt,1,Pyt,1,Pzt,1]T；[Pxt,2,Pyt,2,Pzt,2]T分别为1号、2号发动机推力矢量在箭体系的分量表示；mg为重力；Qeng,1，Qeng,2分别为1号、2号发动机的耗油率，单位为kg/s。

气动力矩、推力力矩等的合外力矩在箭体系的分量[Mxt,Myt,Mzt]T可表示为：

(6)

式中，[L,M,N]T为箭体系下的气动力矩；[lx,1,ly,1,lz,1]T，[lx,2,ly,2,lz,2]T分别为1号、2号发动机转轴在箭体系相对于飞行器质心的坐标；⊗表示矢量的叉乘，其定义为：

(7)

飞行器地速大小v按下式计算：

(8)

地面系下的空速按下式计算：

(9)

箭体系下的空速按下式计算：

(10)

空速大小按下列2式计算均可：

(11)

(12)

飞行器攻角α和侧滑角β根据下2式计算：

(13)

(14)

其中，α∈[-π，π]。

2.3.3 气动特性

气动力和力矩需要计算相应的气动系数。记：

CA,CN,CZ,Cmx,Cmy和Cmz分别为轴向力系数、法向力系数、侧向力系数、滚转力矩系数、偏航力矩系数和俯仰力矩系数，正方向为其所在(或所绕)箭体系坐标轴的正方向。

气动系数是空速、攻角和侧滑角非线性函数，其标称值以多维数表的形式给出：

Ck=Ck(u,α,-β) (k=A,N,Z,mx,my,mz)

箭体系下气动力为：

Fk=qSrefCk(k=A,N,Z)

(15)

气动力矩系数的参考点为飞行器顶点。因此，箭体系下绕质心的气动力矩为：

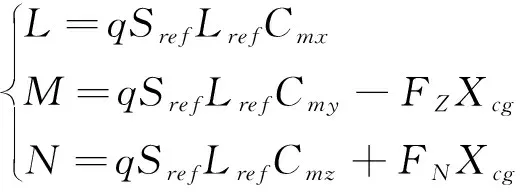
(16)

式中，Sref为气动参考面积;Lref为气动参考长度;Xcg为质心位置，从飞行器顶点向下为正；q为动压：

(17)

其中，ρ为大气密度;u为空速大小。计算时，气动力系数、气动力矩系数、质心位置和大气密度均应考虑偏差。

2.3.4 发动机推力矢量

发动机的摆动由伺服电机驱动实现。每台发动机由4个电机驱动(可等效为2个舵机)，每台发动机的2个舵机互不耦合，分别在正交的2个方向产生摆角，控制发动机向任意方向偏转。2台发动机呈“一”字形安装。每台发动机有俯仰、偏航2个转轴。其后视图如图2所示。

图2 孔雀飞行器发动机安装与摆角定义示意图

结合发动机摆角的定义，2台发动机的推力矢量分别为：

(18)

其中，δins为安装角，即摆角为零时发动机推力线与箭体轴线夹角，以使得推力线由平行于箭体X轴偏向质心方向。

2.4 执行机构模型

2.4.1 发动机推力变化的动态特性

“孔雀”飞行器发动机采用JETCAT P550 Pro，发动机推力变化特性可表示为如下形式：

PC=f(PWMeng)

(19)

其中推力指令是发动机控制PWM信号PWMeng的函数，由数表插值得到，PWMeng是一个正整数。若某一自变量的值超出插值表，则以数表边界值代替。

根据地面测试数据，将发动机动态特性简化为一个二阶线性环节，用于计算实际推力。

(20)

式中，PC为推力指令;P为发动机实际推力大小;Keng为发动机稳态增益;ωeng为发动机自然频率；ξeng为发动机阻尼比。

2.4.2 驱动发动机摆动的伺服电机动态特性

将电动舵机的动态特性简化为二阶传递函数、间隙特性与零位的串联。

二阶传递函数特性如下：

(21)

式中，δ*C(s)为摆角指令;δ*TF(s)为经过传递函数后的舵机摆角。下标*表示1,2,3,4。Kδ为伺服稳态增益，ωδ为伺服自然频率，ξδ为伺服阻尼比。

3 模型参数

本文所列各飞行器相关参数来源于设计过程中的计算数值或根据飞行试验数据所测得的值。

3.1 飞行器总体参数

孔雀飞行器模型参数见表2：

表2 孔雀飞行器总体参数标称值

3.2 气动系数

分别在起落架收起上升段、无栅格舵起落架收起下降段2种状态下，根据试验数据进行拟合。飞行器在上升段与下降段，在起落架收起与起落架放下的状态下，其气动特性均有不同。受篇幅限制，本文未列出模型仿真过程中所采用的气动参数，对此部分感兴趣的读者可通过作者邮箱进行索取。

3.3 发动机参数

发动机参数的标称值见表3。

表3 发动机参数标称值

3.4 伺服电机参数

伺服电机参数的标称值见表4。其中伺服间隙半宽度大小为通过试验实测。

4 控制仿真实例

本仿真实例采用一套制导控制律对模型进行控制，目标为将“孔雀”飞行器由起点(0m,0m,0m)起飞，在终点(40m,0m,0m)处着陆，在飞行过程中以上升速度(Y向速度)10m/s经过交班点(40m,320m,0m)，在经过交班点之后开始减速上升，至最高点后进行加速下降，当速度达到-7m/s时进行减速下降直至着陆。受篇幅限制，本文未列出模型仿真过程中所采用的制导与控制算法，对此部分感兴趣的读者可通过作者邮箱进行索取。

表4 伺服电机参数标称值

飞行器运动方程与制导控制律均通过MFC环境进行编程，对于模型中的微分方程，采用固定步长的四阶龙格-库塔法进行数值积分。仿真开始时间为ts=0.0s，积分步长为Δt=0.001s,控制周期ΔtC=0.01s。图3～4分别为仿真过程中飞行器的位置、速度曲线。可见按照所设定的制导控制律，可完成飞行器按照预定轨迹在47.32s左右飞至交班点，并垂直降落至指定位置。图5～6为真实飞行试验中采用相同的制导控制律得出的真实飞行试验曲线。从曲线的趋势可以看出，该模型能够较为相似地反映实际飞行控制状态。

图3 飞行控制仿真位置速度曲线

图4 飞行控制仿真姿态曲线

图5 实际飞行试验中飞行器位置速度曲线

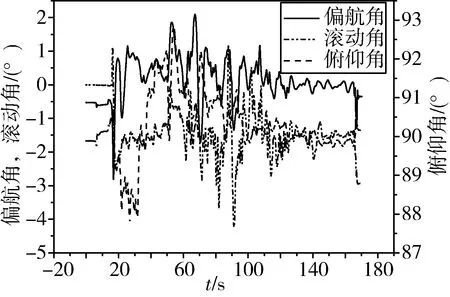
图6 实际飞行试验中飞行器姿态曲线

5 结论

本文介绍了“孔雀”飞行器垂直起降飞行验证平台的数学模型，以微分方程的形式描述了该模型的运动学方程、气动特性和发动机及伺服机构等执行机构特性，并基于本模型采用一套制导控制律进行了飞行控制半实物仿真。该数学模型可作为被控对象用于运载火箭垂直回收技术等飞行控制技术的仿真研究。