一种卫星姿态控制系统故障定位研究方法*

何漫丽 程月华 韩笑冬 王 泽 叶正宇

1.南京航空航天大学航天学院，南京 211100

2.南京航空航天大学自动化学院，南京 211100

3.中国空间技术研究院，北京 100094

0 引言

随着航天技术的不断发展，对卫星的安全性和可靠性的要求越来越高。一旦发生故障，会导致卫星无法完成空间任务，因此实现卫星的故障诊断尤为重要。在卫星系统中故障数据非常少，而现有的机器学习和数据挖掘等算法大多要求大量且高质量的故障数据，因此这些方法在实际卫星故障诊断中难以应用。

近些年来，基于数据驱动的故障诊断方法不依赖精确的系统数学模型或专家经验，已成为卫星故障诊断的重要方法[1]。文献[2]提出了基于多层前馈神经网络方法对航天器在线故障检测提供支持。文献[3]采用神经网络对飞轮进行建模，对单个飞轮进行检测以定位故障。文献[4]使用神经网络分别对动量轮和地球敏感器建模分别检测以定位故障。文献[5]采集了飞轮总线电压，使用神经网络对反作用飞轮进行建模检测故障。这些研究方法依赖大量的故障样本[6-7]，而实际卫星系统难以获得足够数量有标签故障样本，迁移学习为解决无故障样本的问题提供了一条有效的方法。

TCA[8]方法是一种基于特征的迁移学习方法，该方法通过将数据映射到迁移子空间中，减小域之间的边缘分布差异，然后利用主成分分析(PCA)方法进行降维，实现分类、回归和聚类。文献[9]针对滚动轴承实际工况的复杂性和变异性导致的故障特征不可预测问题，采用TCA方法进行跨域特征提取，实现滚动轴承故障诊断。文献[10]通过转移成分分析方法将不同域的数据映射到共享的潜在空间，从而减小训练和测试数据之间的分布差异，提高了异步电机在不同工况下的故障诊断性能。文献[11]利用TCA实现了三相异步电机定子故障的在线诊断。因此本文引入TCA方法，解决实际卫星无故障样本情况下的故障定位问题。

本文提出一种基于迁移成分分析的卫星姿态控制系统故障定位方法。首先以设计阶段的卫星模型和在轨卫星分别作为标称模型和实际模型，利用标称模型和实际模型的健康数据拟合ACS系统模型，生成残差信号，提取故障特征。以标称模型残差特征、实际卫星残差信号分别作为源域、目标域数据，利用TCA方法进行特征变换，以减小源域和目标域的残差特征分布差异，解决在轨卫星的故障诊断问题。经过半物理仿真平台试验，验证了所提出算法的有效性。本文的结构安排如下：第1节从残差角度分析了迁移学习的可行性；第2节提出了本文的研究方案；第3节利用半物理气浮台仿真验证了本文所提方案；第4节对本文所展开的研究工作进行了总结。

1 问题描述

考虑航天器传感器安装不确定性、转动惯量不确定性及环境干扰，用状态方程描述航天器实际系统方程如式(1)所示。

(1)

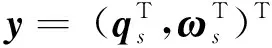
1.1 数据拟合的标称卫星模型的残差信号

记航天器的标称模型如式(2)所示。

(2)

针对标称模型建立神经网络观测器如式(3)所示。

(3)

(4)

(5)

将式(5)代入式(4)中，可得式(6)。

(6)

1.2 数据拟合的在轨卫星残差信号

由于航天器遥测数据中包含了执行器不确定性ΔB、环境扰动Md、敏感器安装误差ΔC，所以通过数据训练建立出来的模型可以表示为式(7)。

(7)

(8)

将式(5)代入(8)，可得式(9)。

(9)

1)根据式(6)和(9)，由于fa和fs的存在，系统健康和故障情况下的信号残差ey存在差异，因此健康数据和故障数据残差具有可分性。

2)比较式(6)和(9)，由于存在执行器安装误差ΔB、敏感器安装误差ΔC、执行器噪声建模误差eεa、敏感器噪声建模误差eεs，标称模型与实际系统的健康数据残差之间存在差异，同时故障数据之间也存在差异。若直接将标称系统的健康和故障数据训练的分类器用于实际系统数据的诊断，一般无法得到较好的诊断效果。

3)由于ΔB、ΔC、eεa、eεs有界，且ΔB、ΔC相对于B、C较小，因此源域与目标域残差数据分布存在相似性，利用域间数据分布的相似性实现迁移学习。

2 基于TCA的故障诊断方案

针对实际卫星无故障样本的问题，利用标称仿真模型与实际卫星系统信号残差特征分布的相似性，采用TCA方法对源域和目标域数据进行特征映射，减少其分布差异，使得标称仿真模型数据训练的分类器能够直接用于目标域数据的诊断。

2.1 故障诊断方案

为了解决实际卫星无故障样本的问题，采用基于TCA的卫星执行器故障诊断方案如图1所示。

图1 TCA诊断方案

Step 1：建立神经网络观测器，生成残差信号

根据卫星ACS系统模型，参考文献[12]设计执行器与动力学观测器Γ1、运动学观测器Γ2。观测器采用反向传播(BP)神经网络进行拟合。观测器Γ1的输入输出分别为[Mc(t),ωs(t)]、ωs(t+Δt)；观测器Γ2的输入输出分别为[ωs(t),qs(t)]、qs(t+Δt)。式中：Δt为控制周期。上述2个观测器Γ1、Γ2均需用标称模型数据和实际系统数据进行训练。建立卫星的标称仿真模型。采集标称模型健康数据训练神经网络观测器Γs。采集实际系统健康数据对Γs继续训练得到实际系统的神经网络模型Γt。

采集标称模型的健康和故障信号输入观测器Γs，将神经网络观测器的输出与标称模型实际输出信号比较，生成残差rs；将采集的实际系统的待检测信号输入训练的神经网络Γt，然后将神经网络Γt的输出与卫星实际输出信号比较，生成残差rt。

Step 2：特征提取与特征映射

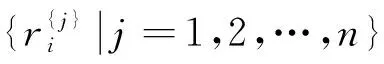
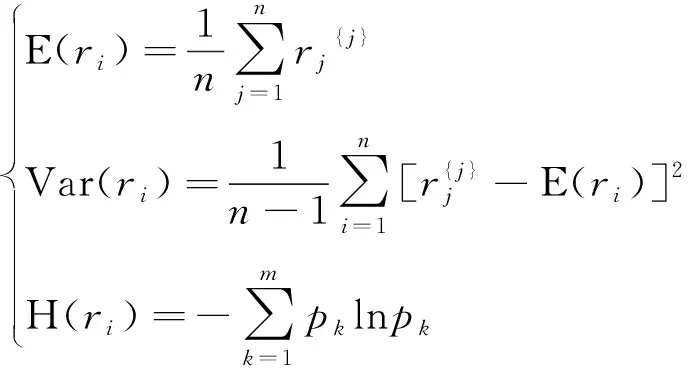
(10)

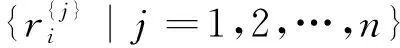
Step 3：Softmax分类器训练与故障诊断

Step 4：结合观测器Γ1、Γ2的观测结果，实现卫星姿态控制系统的故障定位[12]。

2.2 TCA算法用于故障诊断

TCA是一种经典的基于特征的迁移学习方法，其利用MMD方法衡量源域和目标域残差特征的距离，并将迁移学习与PCA方法结合，对数据进行特征映射，以减小数据特征分布差异，使得源域数据特征训练的分类器能用于目标域数据的诊断[8]。

1)MMD(Maximum Mean Discrepancy)

在迁移学习中，很多度量方法被用于衡量数据分布的距离，如余弦相似度、KL散度、A-distance等。文献[13]提出一种最大均值差异(MMD)方法作为衡量两个分布之间距离的标准。它通过将原空间中两组数据通过Φ映射到再生核希尔伯特(RKHS)空间，通过计算再生核希尔伯特空间中样本均值的欧氏距离得到样本分布距离。设Xs={x1,…,xns}和Xt={x1,…,xnt}是两组数据样本，则其概率分布P(Xs)和P(Xt)之间的距离为：

(11)

式中：H是高维的希尔伯特空间，Φ:χ→H，Xs∈χ,Xt∈χ。将式(11)展开得到式(12)：

D(Xs,Xt)=tr(KL)

(12)

式中：

(13)

2)TCA

设源域数据Xs和目标域数据Xt边缘概率分布P(Xs)≠P(Xt)，且条件概率分布P(Ys|Xs)≠P(Yt|Xt)。假设存在一个映射ψ，使得ψ(Xs)与ψ(Xt)的分布相近，即p(ψ(Xs))=p(ψ(Xt))， 然后可以针对ψ(Xs)和Ys使用标准的机器学习算法训练分类器，用于ψ(Xt)的类别Yt。

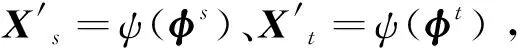
(14)

则有：

(15)

引入核矩阵K使得K(·,·)=〈φ(ψ(·)),φ(ψ(·))〉，则根据式(12)，优化问题可以变成最小化式：

(16)

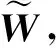
(17)

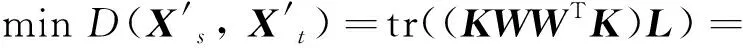
(18)

加入正则化项后，优化目标为：

(19)

式中：tr(WTW)为正则化项，避免W太过复杂。限制WTKHKW=I作用是避免得到W=0的解。μ为正则化项参数，H是一个中心矩阵，H=Ins+nt-1/(ns+nt)11T，Ins+nt∈R(ns+nt)×(ns+nt)，1∈Rns+nt。

用拉格朗日乘子法解式(19)，有：

tr(WTKLKW)+μtr(WTW)-
tr((WTKHKW-I)Z)=
tr(WT(KLK+μI)W)-tr((WTKHKW-I)Z)

(20)

设式(20)对W的导数等于0，有：

(KLK+μI)W=KHKWZ

(21)

式(21)两边同乘以WT得：

WT(KLK+μI)W=WTKHKWZ⟹
Z=(WTKHKW)+WT(KLK+μI)W

(22)

将式(22)中Z代入(21)得到：

tr(WTKHKW)+WT(KLK+μI)W)

(23)

式中：+为伪逆符号。由于KLK+μI矩阵非奇异，最小化式(23)等价于：

(24)

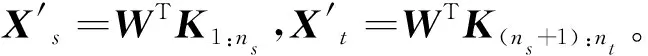
3 故障诊断技术的半物理仿真校验

为了验证本文提出的基于TCA的卫星ACS系统故障定位方法的有效性，以气浮台模拟在轨卫星，开展基于三轴气浮台的半物理仿真验证。

建立标称卫星模型仿真系统作为源域，以微型气浮半物理仿真平台作为目标域，验证在气浮台无故障样本的情况下，利用标称模型仿真数据特征建立Softmax分类器，用于对气浮台待检测样本的诊断。微型三轴气浮台设备如图2所示。

图2 微型三轴气浮平台系统

微型气浮台的设计质量m=31kg，设计惯量Js，飞轮角动量Jw=0.438Nms由于存在制造误差、安装误差、干扰力矩等因素作用，实际气浮台参数与设计参数存在差别。

其中

(25)

以飞轮故障为例，图3为源域和目标域的正常和故障数据的x轴角速度残差特征以及通过TCA特征映射后的三维特征。

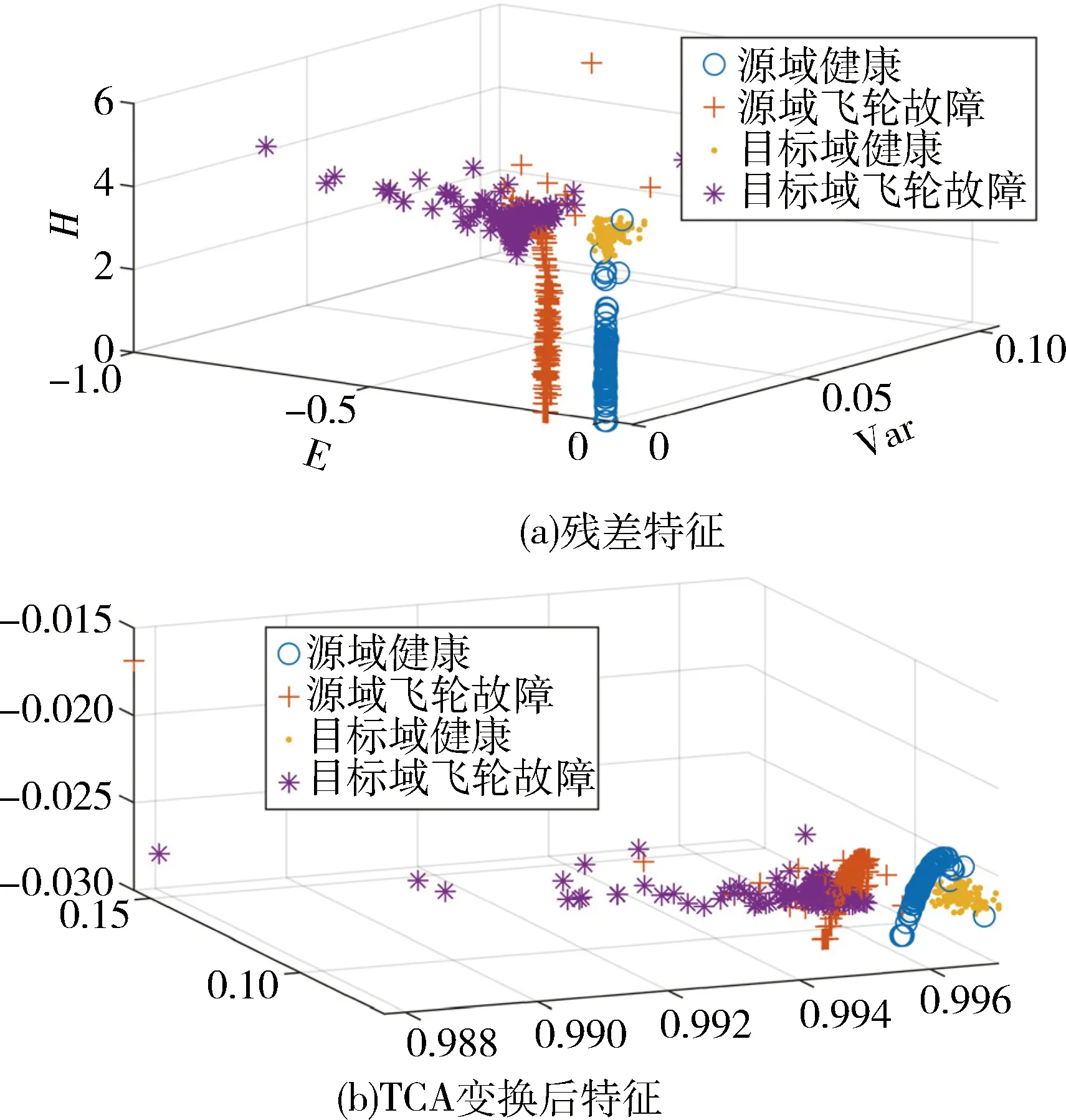
图3 残差特征和利用TCA变换后特征

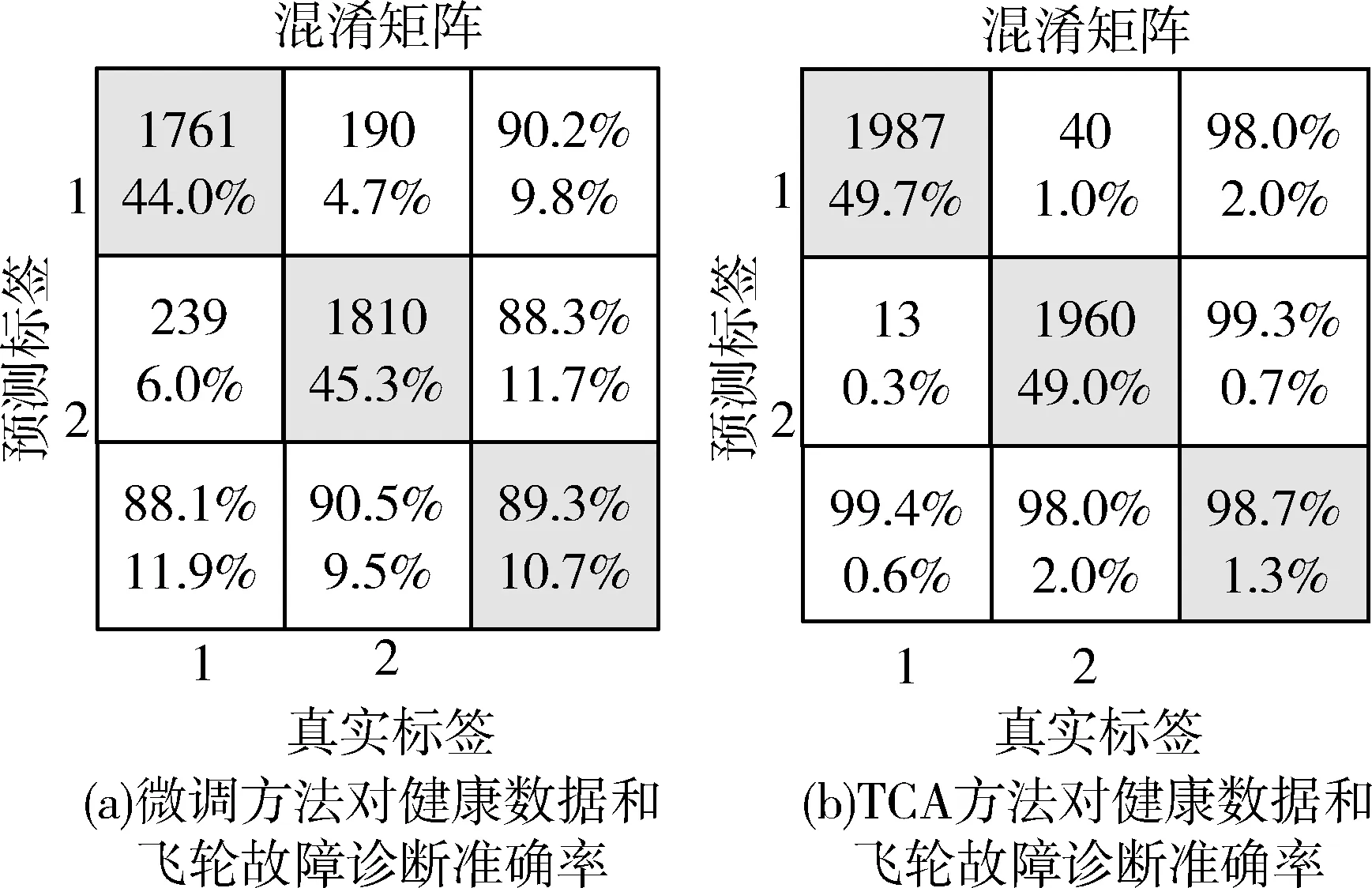
图4 softmax故障检测结果

参照Step4，得到各部件故障定位准确率如图5所示。从图5可以得到，仅用微调的迁移学习方法对健康、飞轮故障、陀螺故障、星敏感器故障样本的故障准确率分别为88.05%、90.52%、97.45%、88.21%，采用TCA改进后的方法对前述几种故障的诊断准确率分别为98%、99.3%、99.89%、92.1%，有效提升了对气浮台的故障定位效果。

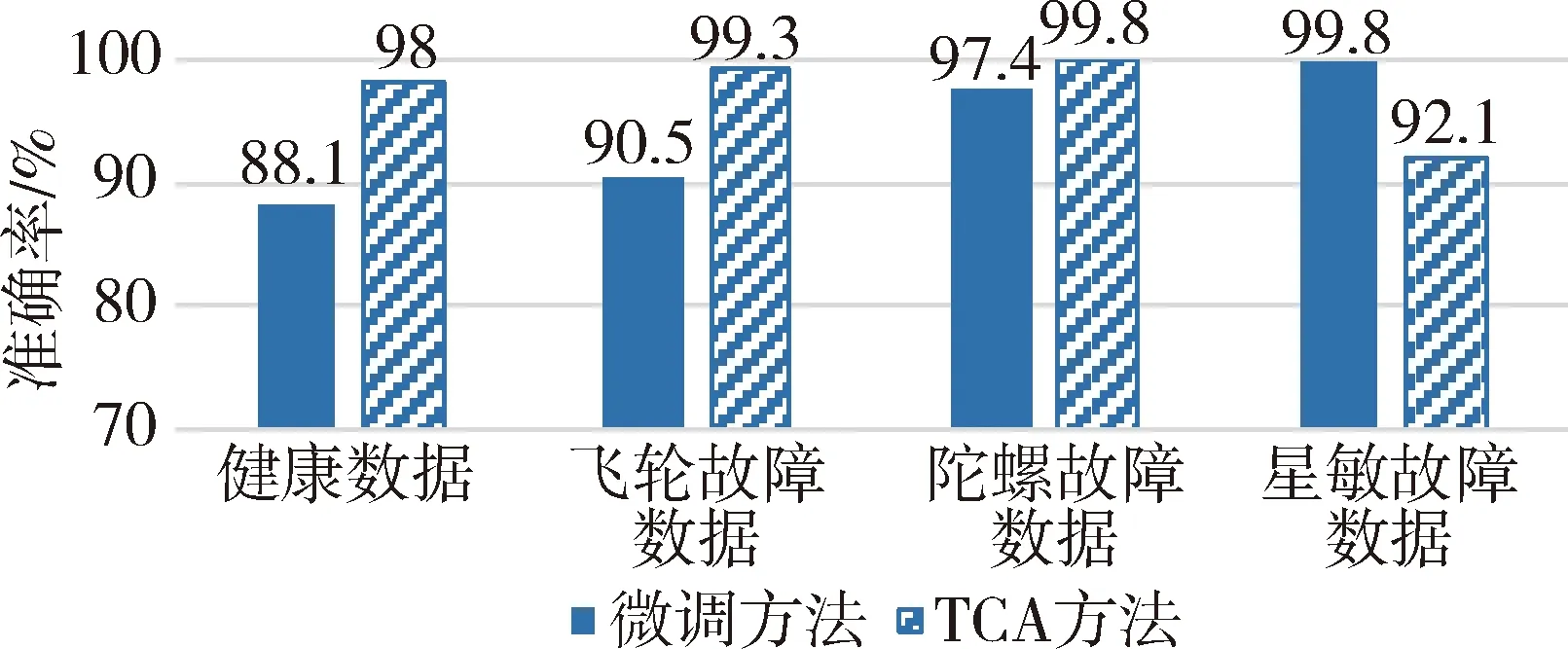
图5 故障定位准确率

4 结论

采用一种基于迁移成分分析与神经网络和softmax结合的方法，用于解决无故障样本情况下的故障定位问题。通过观测器获得数据残差并提取残差的故障特征后，采用TCA方法减小了残差特征分布差异，实现了源域特征训练的Softmax分类器对目标域待检测数据进行诊断。相较于未使用TCA的微调方法，本文所提方法明显提高了故障定位准确率。