计及电压环影响的虚拟同步发电机低频振荡阻尼分析与控制

王光宇，付立军，胡 祺，刘陈瑞扬，马堰泓

（舰船综合电力技术国防科技重点实验室（海军工程大学），湖北省武汉市 430033）

0 引言

为响应国家“双碳”战略目标，加速推进能源结构转型，以光伏、风电等为代表的新能源发电在电网中的渗透率不断提高［1-2］。与同步发电机不同，以采用常规控制方案的电力电子变换器为并网接口的新能源发电机不具备旋转惯性，其低惯量和弱阻尼特点给电力系统安全稳定运行带来了新的挑战。为此，逆变电源的虚拟同步发电机（virtual synchronous generator，VSG）控 制 技 术 应 运 而生［3-7］，其通过控制模拟同步发电机的运行特性，从而使其具备主动支撑电网的能力。

然而，VSG 在模拟同步发电机运行特性的同时，也继承了同步发电机潜在的稳定性问题。在传统电力系统中，由于远距离输送电的需要，同步发电机中存在着高倍数的快速励磁控制器，当它产生的负阻尼转矩大于发电机固有的正阻尼转矩时，可能导致系统低频振荡［8］。类似的问题也出现在VSG中，文献［9-10］研究了VSG 并网运行时存在的功率振荡问题，发现无功-电压控制环节有着和同步发电机励磁控制相似的负阻尼作用，容易诱发系统振荡失稳。文献［11］揭示了锁相环对VSG 低频振荡的作用机理，得出减小锁相环带宽或增大虚拟阻抗可以有效改善锁相环引入的负阻尼影响。文献［12-13］分别从原动机控制和VSG 渗透率的角度入手分析了VSG 存在的低频振荡失稳风险。因此，VSG在模拟同步发电机工作的同时，也会继承同步发电机的转子振荡特性，系统可能存在以转子运动方程为主导的低频振荡问题［14-15］。上述文献虽然从不同角度对VSG 并网系统的低频振荡问题进行了研究，但鲜有文献计及VSG 内环电压-电流双闭环尤其是动态响应相对较慢的dq轴电压控制的影响。

对于以电力电子变换器为并网接口的新能源发电机而言，电压-电流双闭环控制在改善系统输出电压和电流动态特性以及过流保护等方面发挥着不可或缺的作用［16-18］，然而，对于其潜在的失稳风险却关注较少，在研究VSG 低频振荡问题时常常被忽略，近年来已有部分研究者开始关注该问题。文献［19］通过对比VSG 向量模型和全动态模型讨论了内外环控制间的耦合问题。文献［20］研究了光伏VSG并网系统中电压环引发的高频谐振和次同步振荡问题。上述研究表明，VSG 内外环控制之间存在一定的耦合影响，但并未对影响机理进行深入讨论。随着变电站功率等级的提升，开关频率趋于减小以降低开关损耗［21］，受限于较低的开关频率，VSG 中级联结构控制的带宽相对较窄，导致各控制环节间时间尺度分离不明显并存在动态交互，电压环对VSG中转子运动方程主导的低频振荡阻尼影响值得评估。文献［22-23］分别基于多回路交互保结构模型和运动方程模型探讨了VSG 内环控制对系统阻尼的影响规律，但建模过程较为复杂，且均没有对改进措施作进一步研究。

本文从VSG 多时间尺度控制特性的角度出发，基于分析将内环控制与虚拟转子运动的耦合交互问题聚焦到动态响应相对较慢的电压环上，建立了计及电压环影响的类Heffron-Phillips 动力学稳定分析模型，利用阻尼转矩法清晰地揭示了电压环对VSG并网系统低频振荡的影响机理，进而根据阻尼特性分析提出了一种基于相位补偿的电压环改进控制方法。最后，通过仿真验证了阻尼特性分析结论的正确性和改进控制方法的有效性。

1 小信号稳定分析模型

1.1 系统结构及多尺度控制特性

典型的VSG 并网系统拓扑结构如图1 所示。

图1 VSG 并网系统结构Fig.1 Grid-connected system structure of VSG

VSG 是通过控制逆变器模拟同步发电机运行来实现惯性支撑的，因此VSG 既含有电力电子器件本身具备的快速响应特性，又存在与同步发电机类似的机电控制特性，控制环节复杂且呈现宽频带特征，如附录A 图A1 所示。由于开关频率的限制，电流环控制带宽通常在百赫兹级，电压环是电流环的相邻控制环路，其动态响应速度通常为电流环的1/10，控制带宽一般为10 Hz 级，而转子运动方程和无功电压控制是模拟同步发电机的机电尺度特性，其控制带宽在赫兹级［24-25］。根据不同控制环节的带宽以及多时间尺度理论，可以近似将VSG 的动态特性划分为3 个尺度:低频尺度、次/超同步尺度、高频尺度。不同的控制尺度对应着不同的小扰动稳定性问题，因此VSG 存在着以低频振荡、次/超同步振荡、高频振荡为代表的宽频带振荡问题，本文关注由转子运动方程主导的低频振荡问题，并着重考虑其相邻时间尺度dq轴电压环控制的动态交互影响。

1.2 稳定分析模型

基于上述分析，可对原有控制拓扑进行简化，得到包含转子运动方程、无功-电压控制以及dq轴电压环的VSG 简化控制拓扑，如附录A 图A2 所示。电流环因具有较高的控制带宽，在低频振荡阻尼分析时可近似等效为增益为1 的放大环节。值得注意的是，对电流环进行简化是为了在机理分析过程中更加清晰直观地研究电压环的影响，而在本文所搭建的仿真模型中则考虑了电流环的动态过程。

采用空间矢量和复杂传递函数表示方法［26］，基于电路关系可得VSG 的输出电压和电流动态为:

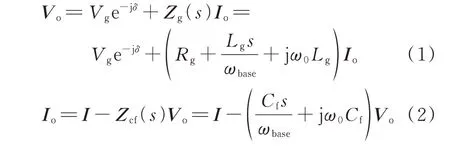
式中:Vo=Vod+jVoq为VSG 输出端电压矢量，其中Vod和Voq分别为输出端电压的d轴和q轴分量；I=Id+jIq和Io=Iod+jIoq分别为逆变器侧和网侧电流矢量，其中Id和Iq分别为逆变器侧电流的d轴和q轴分量，Iod和Ioq分别为网侧电流的d轴和q轴分量，上述矢量均建立在控制器自身的dq旋转坐标系下；δ=θVSG-θg为控制器dq旋转坐标系相位θVSG与电网dq旋转坐标系相位θg的差值；Zg（s）和Zcf（s）分别为线路和滤波器阻抗的矢量形式；Vg为电网电压幅值；ωbase和ω0分别为频率基准值和额定值。

忽略电流环动态影响，逆变器侧输出电流矢量等价于电压环输出电流参考矢量，其动态方程可表示为:

式中:Gvc（s）=Kvp+Kvi/s为电压环PI 控制器的传递函数，其中Kvp和Kvi分别为电压环的比例和积分系数；E=E+j0 为VSG 端电压参考矢量，d轴分量E由无功-电压控制环节决定，通过设置q轴分量为0保证VSG 初始端电压矢量位于控制器d轴上。

无功-电压控制环节模拟同步发电机的无功调压特性，其动态方程为:

式 中:Vod，0和Vo，0分 别 为 输 出 端 电 压d轴 分 量 和 输出端电压幅值在平衡点处的稳态值；传递函数XE(s)代表控制器相位扰动对无功-电压控制环节输出电压指令的影响。

式中:ΔTD为阻尼转矩，由虚拟转子运动自身控制参数决定，ΔTD=DΔω；ΔTE为等效电磁转矩，反映复杂控制环节的耦合影响，ΔTE=ΔTE1+ΔTE2=(GE1(s)+GE2(s))Δδ，其中转矩ΔTE1受到电压环和电路参数影响，转矩ΔTE2由电压环、无功-电压控制环节和电路参数共同作用。稳定分析模型基于VSG 转子运动方程，其他控制回路可看作是向转子运动提供等效的输入转矩，阻尼转矩ΔTD和等效电磁转矩ΔTE合成得到的总输入转矩ΔT∑决定虚拟转子的摇摆特性。

图2 稳定分析模型Fig.2 Stability analysis model

1.3 模型验证

为验证本文所建立稳定分析模型的正确性，在MATLAB/Simulink 中分别建立VSG 稳定分析模型和详细的电磁暂态模型，详细模型考虑了电流环的动态过程，主要参数见附录A 表A1。在2 s 时，系统有功功率指令Pref阶跃增加0.1 p.u.，4 s 时阶跃减少0.2 p.u.，2 种模型对应的输出功率动态响应见附录A 图A3。由图A3 可以看出，二者的暂态响应过程具有较好的一致性，验证了稳定分析模型的有效性。

2 电压环对低频振荡阻尼特性的影响分析

2.1 电压环对阻尼特性的影响机理分析

前文建立了VSG 低频振荡稳定分析模型，控制环节对阻尼特性的影响可看作向转子运动方程提供等效的输入转矩。根据经典电力系统稳定性分析理论可知，输入转矩可以分解为阻尼成分和同步成分，只有同时具备正阻尼成分和正同步成分的系统才是小扰动稳定的，其中阻尼成分可以定量衡量系统对低频振荡的抑制能力，为弱阻尼低频振荡模式的形成提供机理解释［27-28］。

考虑电压环影响的VSG 阻尼转矩分析如附录A 图A4 所示。图A4（b）中给出了等效电磁转矩传递函数的波特图，由图A3 可知此时系统的主导振荡频率在1～2 Hz 之间，根据主导振荡频率对应的幅值和相位可得对应的等效电磁转矩ΔTE，如图A4（a）所示。分析可知，VSG 的阻尼成分由两部分组成，一部分是由转子运动自身参数决定的固有阻尼成分，另一部分是由复杂控制耦合引入的附加阻尼成分。特别地，当负的附加阻尼成分大于正的固有阻尼成分时，系统则会因阻尼不足而发生低频振荡。

同样的，可以建立忽略电压环影响的VSG 稳定分析模型，仅考虑转子运动方程和无功-电压控制环节的影响，其控制拓扑及模型推导见附录C。忽略电压环影响的VSG 阻尼转矩分析结果如附录A 图A5 所示，相似的，可以求得其等效电磁转矩ΔTE，进一步分解得到Δω轴上的附加阻尼成分。通过对比图A4（a）和图A5（a）可以发现，考虑电压环影响的VSG 和忽略电压环影响的VSG 固有阻尼成分相同，而前者的附加阻尼成分明显大于后者，因此计及电压环影响的VSG 系统总阻尼成分较小，低频振荡阻尼特性较差。换而言之，电压环的引入给VSG 系统提供了额外的负阻尼成分，从而恶化了VSG 低频振荡阻尼特性，增加了系统低频振荡失稳的风险。

2 种情形下的VSG 低频振荡模式对比如表1 所示。可以看出，考虑电压环影响的VSG 低频振荡模式阻尼明显减小，振荡频率增大，其低频振荡模式离虚轴更近，因此电压环恶化了VSG 的阻尼特性，与阻尼转矩分析的结果一致。

表1 不同情形下的低频振荡模式对比Table 1 Comparison of low-frequency oscillation modes in different scenarios

2.2 电压环控制参数的影响分析

基于前文分析可知，电压环的引入给VSG 系统提供了额外的负阻尼成分，进一步分析电压环控制参数对阻尼成分的影响规律。图3（b）中给出了VSG 在不同电压环比例系数下的等效电磁转矩传递函数波特图，根据主导振荡频率对应的幅值和相位可以分别得到对应的等效电磁转矩ΔTE，如图3（a）所示。可以看出，随着电压环比例系数的减小，等效电磁转矩相位减小而幅值基本保持不变，ΔTE向Δω轴负方向靠拢，因此复杂控制耦合所引入的负阻尼成分增大，系统总阻尼成分减小，从而恶化了系统的阻尼特性。值得注意的是，当电压环比例系数足够小时，复杂控制耦合引入的负阻尼成分可能大于VSG 的固有阻尼成分，使得系统总阻尼成分为负，系统可能因阻尼不足而发生低频振荡。

图3 电压环比例系数对阻尼成分的影响Fig.3 Effect of proportional coefficient of voltage loop on damping component

表2 中给出了VSG 在不同电压环比例系数下的低频振荡模式，随着比例系数的减小，电压环所提供的额外负阻尼成分增大，低频振荡模式阻尼减小，系统低频振荡失稳的风险增加，与阻尼特性分析的结果一致。

表2 不同电压环比例系数下的低频振荡模式对比Table 2 Comparison of low-frequency oscillation modes with different proportional coefficients of voltage loop

电压环积分系数对VSG 阻尼成分的影响如图4 所示。与比例系数的作用效果不同，随着电压环积分系数的增大，等效电磁转矩相位基本保持不变而幅值增大，但同样使得转矩ΔTE在Δω轴负方向上的分量增大，从而恶化了系统阻尼特性。

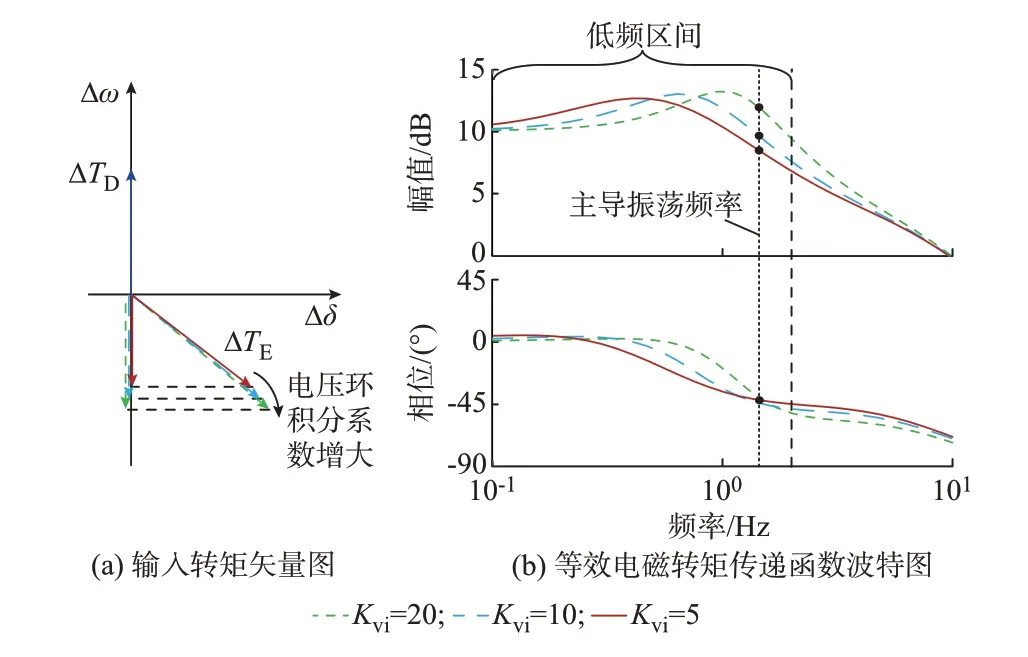
图4 电压环积分系数对阻尼成分的影响Fig.4 Effect of integral coefficient of voltage loop on damping component

表3 中给出了VSG 在不同电压环积分系数下的低频振荡模式，随着积分系数的增大，电压环所提供的额外负阻尼成分增大，系统阻尼比减小，验证了阻尼特性分析结果的正确性。

表3 不同电压环积分系数下的低频振荡模式对比Table 3 Comparison of low-frequency oscillation modes with different integral coefficients of voltage loop

3 基于相位补偿的改进电压环控制

由第2 章分析可知，电压环提供了额外的负阻尼成分，使得VSG 系统总阻尼成分减小，可能带来低频振荡问题。为削弱电压环引入的负阻尼影响，改善VSG 低频振荡阻尼特性，本章基于阻尼特性分析提出了一种基于相位补偿的改进电压环控制策略，通过相位补偿方法重塑等效电磁转矩传递函数的频谱特性，增大电磁转矩ΔTE与Δω轴负方向的夹角，从而减小电压环引入的负阻尼成分，改善VSG 阻尼特性，原理如附录A 图A6 所示。

基于相位补偿的改进电压环控制拓扑如附录A图A7 所示，改进后的电压环动态方程可表示为:

式中:T1和T2分别为超前和滞后时间常数。

相位补偿器所能提供的最大超前相位可由下式计算得到:

相位补偿器的参数设计可按下列步骤进行:首先，选择系统主导模式的振荡频率作为相位补偿器的最大超前相位频率flead；然后，选择合适的最大超前补偿相位φlead；最后，根据所选择的频率flead和相位φlead，联立式（14）和式（15）计算超前和滞后时间常数T1和T2。

选择VSG 的主导振荡频率作为最大超前相位频率，分别选择最大超前补偿相位为10°、30°和50°这3 种情形，另取无相位补偿情形作为对照。分别求解相位补偿器参数T1和T2，如表4 所示。4 种不同补偿条件下的相位补偿器传递函数S（s）的波特图如附录A 图A8 所示。

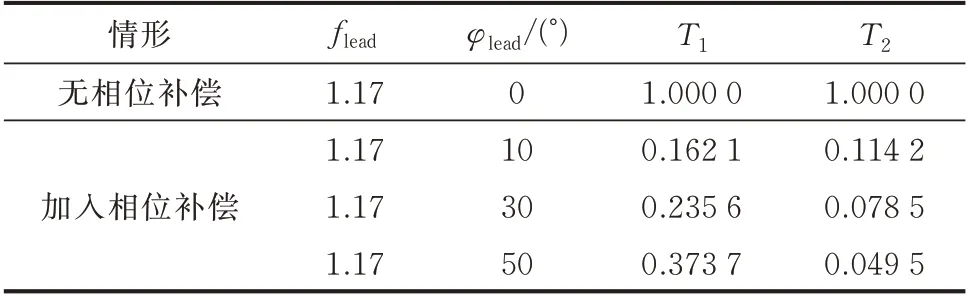
表4 相位补偿器参数设计Table 4 Parameter design of phase compensator

不同补偿相位对VSG 系统阻尼成分的影响如图5 所示。可以看出，系统在加入电压环相位补偿后，主导振荡频率下的等效电磁转矩传递函数相位显著增大而幅值几乎不变，这意味着等效电磁转矩向远离Δω负半轴的方向移动而大小几乎不改变，相应在Δω轴上提供的负阻尼分量显著减小，大大削弱了电压环引入的负阻尼影响。

图5 补偿相位对阻尼成分的影响Fig.5 Effect of compensated phase on damping component

同时，适当地增大相位补偿角度会使得等效电磁转矩的转动角度也相应增大，提供的负阻尼分量减小，更有利于改善VSG 系统的阻尼特性，但相位补偿方法的能力有上限。以本文研究对象为例，当补偿角度超过50°时，等效电磁转矩的补偿角度提升较小，且转矩幅值基本不变，此时再继续增大补偿角度对VSG 低频振荡阻尼没有明显提升，还可能会引入新的同步谐振问题，如附录A 图A9 所示。因此，在应用改进的电压环控制策略时要结合系统阻尼特性选择适当的相位补偿角度，提升VSG 低频振荡阻尼补偿效果的同时，避免引入新的稳定性问题。

4 仿真验证

为了验证VSG 阻尼特性分析的正确性和所提优化控制方法的有效性，在MATLAB/Simulink 中搭建了VSG 并网系统仿真模型，系统控制拓扑如图1 所示，主要参数详见附录A 表A1。

图6（a）给出了计及电压环影响和不考虑电压环影响时VSG 并网系统的小扰动仿真结果。系统初始运行在稳定状态下，2 s 时系统有功功率指令阶跃增加0.1 p.u.，可以看出考虑电压环影响的VSG功率响应曲线相比不考虑电压环影响的振荡幅度较大，且收敛速度较慢，系统阻尼特性较差，更容易发生低频振荡，说明电压环的引入提供了额外的负阻尼成分，使得VSG 总阻尼成分减小，验证了阻尼特性分析的结论。

进一步，考虑电压环主要控制参数对VSG 阻尼特性的影响。不同电压环比例系数下的VSG 输出功率响应波形如图6（b）所示，随着比例系数的减小，输出功率振荡幅度逐渐增大，系统可能由于阻尼不足而发生低频振荡。基于前文对VSG 多尺度特性的分析可知，当比例系数减小时，电压环与转子运动方程之间的动态交互会进一步增强，从而增大了电压环对系统低频振荡的负阻尼影响，恶化了VSG低频振荡阻尼特性。不同电压环积分系数下的VSG 输出功率响应波形如图6（c）所示，当积分系数增大时，输出功率的振荡幅度基本不变，但振荡频率加快，系统恢复稳定的时间延长，电压环引入的负阻尼成分增大，系统阻尼特性变差。

采用改进的电压环控制策略，补偿相位从0°增大到50°时，系统的输出功率响应曲线见图6（d）。可以看出，随着电压环补偿相位的增大，系统低频振荡问题得到改善。根据阻尼特性分析结果可知，当在电压环前向通道加入相位补偿后，系统等效电磁转矩与Δω轴夹角增大，形成的负阻尼分量减小，系统固有阻尼成分不变时总阻尼成分增大，因此适当增大电压环相位补偿角度更有利于改善系统的阻尼特性。

图6 不同条件下的输出功率响应Fig.6 Output power response under different conditions

5 结语

本文按照稳定分析模型建立、阻尼特性分析、改进控制的思路开展了计及电压环影响的VSG 低频振荡阻尼特性分析与控制研究。首先，基于VSG 多尺度控制特性分析，并借鉴同步发电机中Heffron-Phillips 模型建模思路，建立了适用于VSG 低频振荡阻尼特性研究的类Heffron-Phillips 稳定分析模型，从而将包含电压环在内的复杂控制耦合影响等效成虚拟转子运动的额外输入转矩。应用阻尼转矩分析方法，揭示了电压环对VSG 低频振荡阻尼特性的影响机理。以此为基础，提出了一种在电压环前向通道加入相位补偿器的优化控制方法，并分析了其对系统阻尼成分的影响。最后，通过仿真验证了阻尼转矩分析的结果，得到结论如下:

1）VSG 在模拟传统同步发电机动态特性的同时引入了转子摇摆振荡特性，系统存在以转子运动方程为主导的低频振荡模式。

2）电压环给VSG 低频振荡模式引入了额外的负阻尼成分，当电压环比例系数减小或积分系数增大时，其所提供的负阻尼成分增大，从而恶化了VSG 阻尼特性，系统可能因阻尼不足而发生低频振荡。

3）基于相位补偿的改进电压环控制策略可以有效补偿电压环引入的负阻尼成分，增大VSG 低频振荡模式阻尼，且适当增大相位补偿角度更有利于改善系统阻尼特性。

本文主要研究了VSG 单机无穷大系统中电压环对低频振荡模式的负阻尼影响并提出改进策略。下一步将针对多VSG 组网系统，开展低频振荡模式阻尼分析与优化控制研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。