整体钢平台结构体系安全性能研究
朱毅敏 徐 磊 陈逯浩 王少纯张星波 陈俊博
(上海建工一建集团有限公司,上海 200120)
0 引 言
超高层建筑作为一座城市乃至国家的地标性建筑伴随着我国经济的快速发展,也同步进入到高速发展阶段,全国各大城市掀起了超高层建筑的建造潮流,超高层建造技术也获得了长足的发展[1]。整体提升钢平台模架体系(图1)以其封闭性好、安全性高、承载能力强、施工速度快等优点,在诸如上海中心、金茂大厦、白玉兰广场等知名超高层建筑工程中得到应用,获得了较大程度的推广,越来越多地出现于超高层建筑的建造中[2]。

图1 整体提升钢平台模架体系Fig.1 Integral lifting steel platform formwork system
在超高层建筑建造过程中,整体钢平台存在安装、爬升、使用和拆除四种施工阶段[3-4],其中爬升阶段和使用阶段交替重复,是结构分析及安全控制的重难点。超高层建造整体提升钢平台结构体系受力工况较多,如何确保钢平台在高空多次变形、风荷载以及其他不利因素的影响下的安全可靠性显得尤为重要[5-7]。目前,针对整体钢平台施工全过程安全监控的研究与实践已经得到充分开展[8-10],研究表明整体钢平台在超高空施工过程中受风荷载的影响较大[11-12],而目前尚缺少针对整体钢平台可能发生的由复杂施工荷载或装备结构缺陷引起失稳破坏的深入研究[13-14],针对控制整体钢平台安全风险的结构变形预警指标的研究也不充分[15]。
本文设计满足抵抗不同作用的由多系统组成的整体钢平台结构,分析了在不同阶段的竖向荷载与作用,并制定了相应的变形控制指标,采用整体结构进行了施工阶段的工况分析,并根据受力特点布置了自动化监控装置,采集的监测数据与计算结果吻合性较好,有效控制了整体钢平台结构的安全性,为大型装备结构的风险控制提供了一定的支撑。
1 钢平台结构体系
整体钢平台是一套复杂的集成式大型施工装备体系,主要用于超高层钢筋混凝土核心筒筒体结构施工,也适用于平面形状复杂、结构形式多变的超高层钢筋混凝土构筑物施工,特别能适应复杂的多筒体超高层结构的施工。典型的提升式整体钢平台主要由位于顶部的钢平台系统、内外挂脚手架系统、模板系统、位于底部的支撑系统、安装于钢平台上的提升系统及动力控制系统组成(图2)。
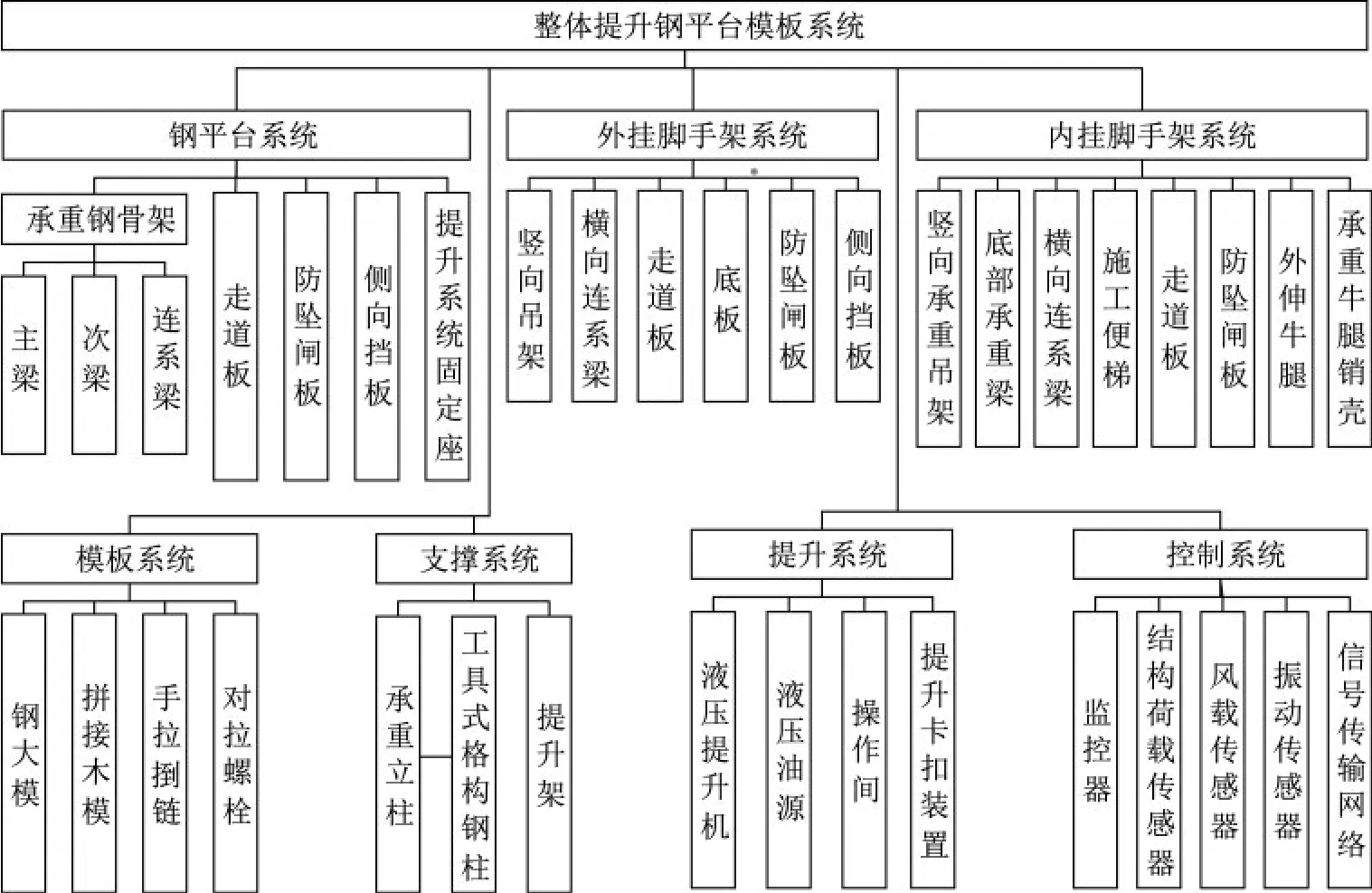
图2 整体钢平台系统功能架构图Fig.2 Functional diagram of the integral steel platform system
2 钢平台结构分析
为设计满足抵抗不同作用的由多系统组成的整体钢平台结构,本文分析了在不同阶段的竖向荷载与作用,采用整体结构进行了全过程理论分析,有效控制了整体钢平台结构的安全性。
2.1 工程概况
昆明恒隆广场主体结构采用劲性柱钢框架-混凝土钢板剪力墙核心筒结构体系,核心筒结构高度为302.95 m,标准层层高为4.3 m。核心筒墙体主要在L35、L36、L50M、L52、L53有5次空中变形,翼墙、腹墙有多次收分,核心筒翼墙厚度地上部分最厚为1 600 mm,最薄为600 mm;腹墙厚度保持600 mm不变,部分楼层有少量300 mm厚的混凝土承重墙。钢平台立面高度12 m,顶梁、底梁、爬升柱及方管柱等构件尺寸、材质见表1。
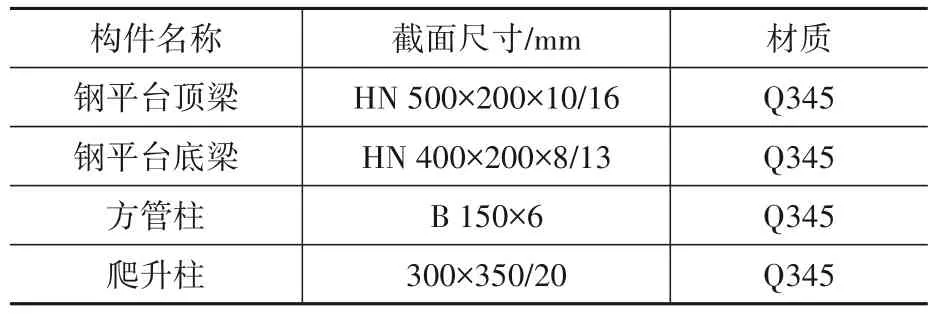
表1 钢平台主要结构参数Table 1 Major structural parameters of the steel platform
本文采用有限元软件MIDAS对钢平台进行了数值模拟,其中主体结构采用梁单元、内脚手吊挂体系采用索单元建立。柱底部的边界条件为铰接,内外支架与核心筒墙体之间为铰接,梁与柱单元之间、梁与梁单元之间根据拆分要求采用刚接、铰接及半刚性连接。钢平台三维有限元模型如图3所示。

图3 钢平台有限元模型Fig.3 Finite element model of the steel platform
2.2 整体钢平台工况分析
本文针对钢平台不同形态、不同工况、不同荷载下安全性和完整性的难题,对不同阶段分别进行设计及受力分析,结合钢平台整体的基本结构形式,进行统一组合,对局部薄弱点进行结构加强,以抵抗钢平台在不同变形阶段的竖向荷载和作用,形成阶段设计与整体分析相结合的钢平台研制模式。
(1)进行钢平台设计时,结合工程实际情况,针对钢平台在不同阶段分别进行设计,考虑不同形态、不同工况及不同荷载要求,依次进行受力分析,以确定钢平台的不同结构形式。图4计算结果表明,本钢平台设计时,正常工作状态和整体提升状态两种工况中各主要构件的应力比均控制在0.84以内,满足钢平台的结构设计要求。阶段设计完成后,结合各个阶段的结果及钢平台基本结构形式,确定整个钢平台的整体布置,最大限度地确保各个不同阶段钢平台整体的完整性及安全性。

图4 钢平台各阶段受力分析结果Fig.4 FE results for each stage of the steel platform
(2)确立钢平台整体结构形式,对薄弱点(牛腿及销壳体)进行加强,以满足钢平台各个阶段的承载力要求,保证钢平台整体模型的可行性。图5计算结果表明,标准牛腿结构悬臂端最大竖向变形为0.796 mm,局部承压区的最大有效应力为267 MPa;重型牛腿悬臂端最大竖向变形为0.419 mm,局部承压区的最大有效应力为240.1 MPa,基本满足结构要求。
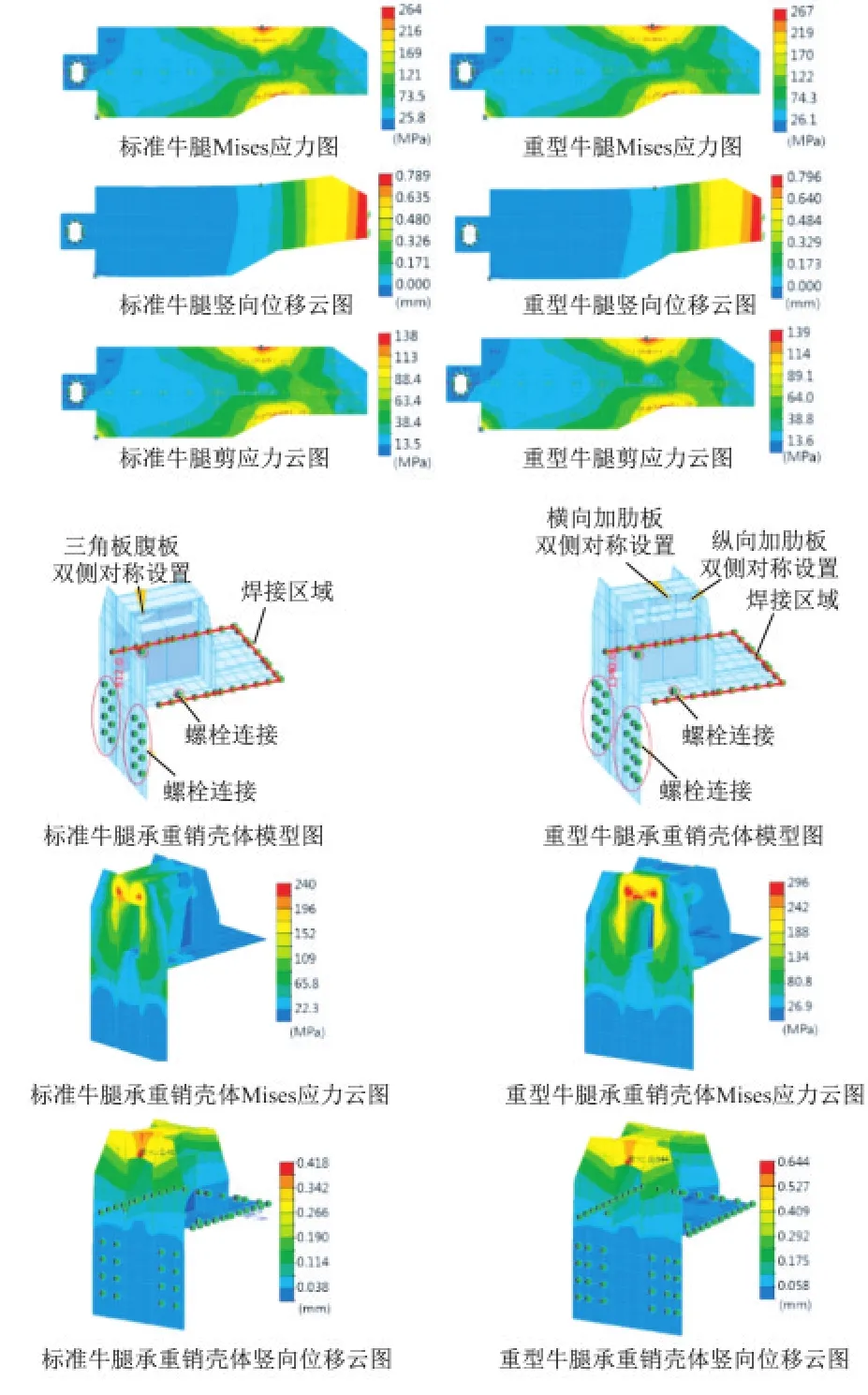
图5 钢平台牛腿及销壳体受力分析结果Fig.5 FE results of the corbel and pin shell of the steel platform
2.3 钢平台结构分析
采用有限元软件Midas对钢平台进行了数值模拟,有限元模型主体结构采用梁单元、内脚手吊挂体系采用索单元建立。柱底部的边界条件为铰接,内外支架与核心筒墙体之间为铰接,梁与柱单元之间、梁与梁单元之间根据拆分要求采用刚接、铰接及半刚性连接。分别选取正常工作状态和整体提升状态进行有模拟分析。
(1)正常工作状态:钢平台主要承重构件最大应力比为0.79(图6)。结构最大竖向变形发生在钢平台顶面四个角部,变形最大理论计算值约56.1 mm(图7)。12级风作用下钢平台X向最大水平位移为18 mm,Y向最大水平位移为14 mm,结构侧向变形比较均匀(图8、图9)。
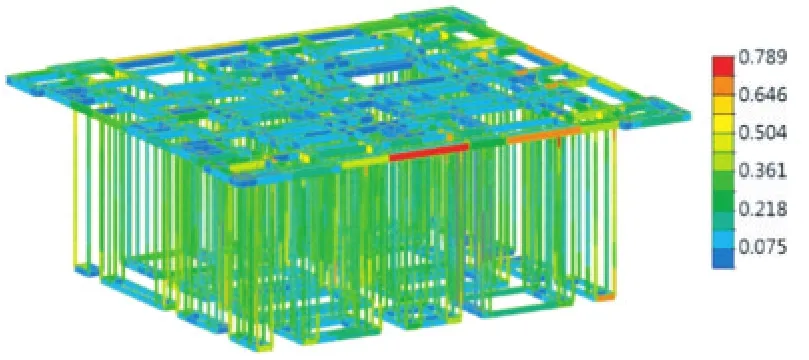
图6 钢平台正常工作状态结构应力比云图Fig.6 Stress ratio contour of the steel platform in working state

图7 钢平台正常工作状态竖向位移云图Fig.7 Vertical displacement contour of the steel platform in working state
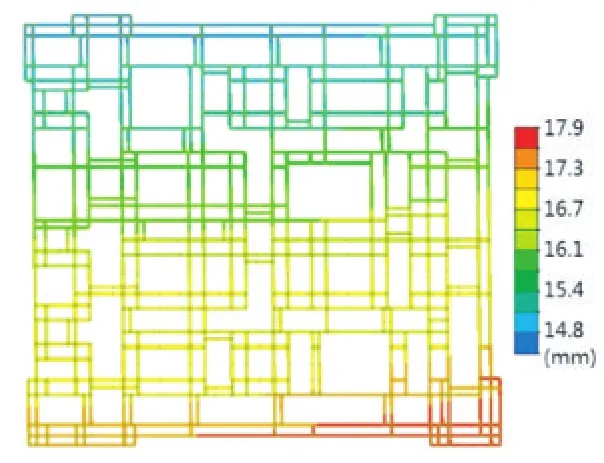
图8 钢平台正常工作状态X向位移云图Fig.8 X-direction displacement contour of the steel platform in working state
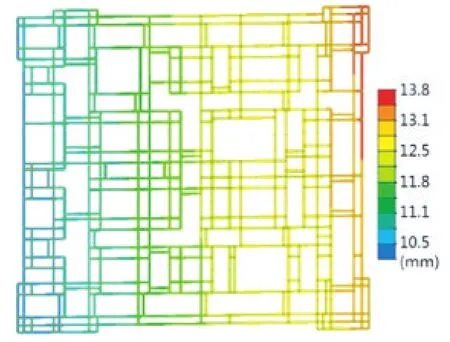
图9 钢平台正常工作状态Y向位移云图Fig.9 Y-direction displacement contour of the steel platform in working state
(2)整体提升状态:对整体结构进行有限元计算分析,从计算结果来看,各杆件应力比均小于0.8,结构设计满足要求(图10)。结构最大竖向变形发生在悬挑较大部位,变形最大理论计算值约40.2 mm(图11)。8级风作用下钢平台X向最大水平位移反应约为13.9 mm,Y向最大水平位移反应约为8.8 mm(图12、图13)。
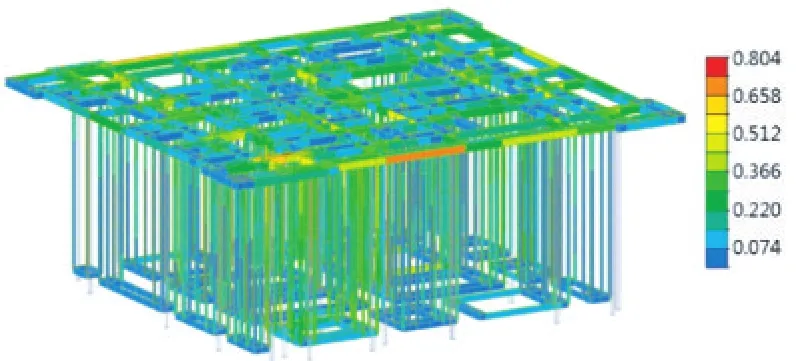
图10 钢平台提升状态结构应力比云图Fig.10 Stress ratio contour of the steel platform in lifting state
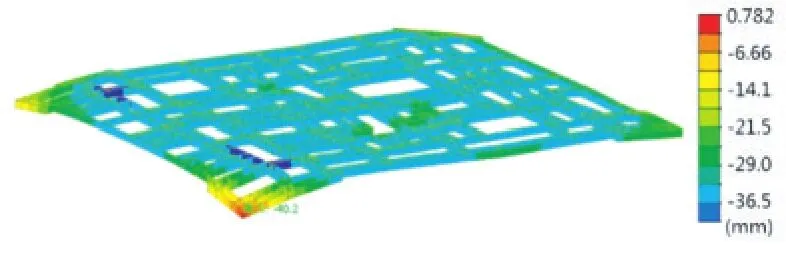
图11 钢平台提升状态竖向位移云图Fig.11 Vertical displacement contour of the steel platform in lifting state
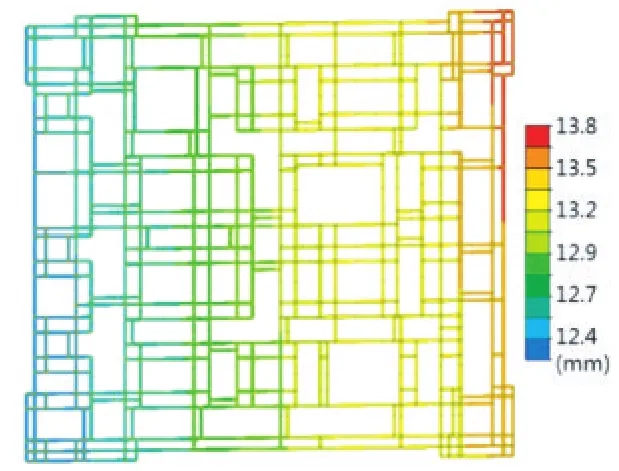
图12 钢平台提升状态X向位移云图Fig.12 X-direction displacement contour of the steel platform in lifting state
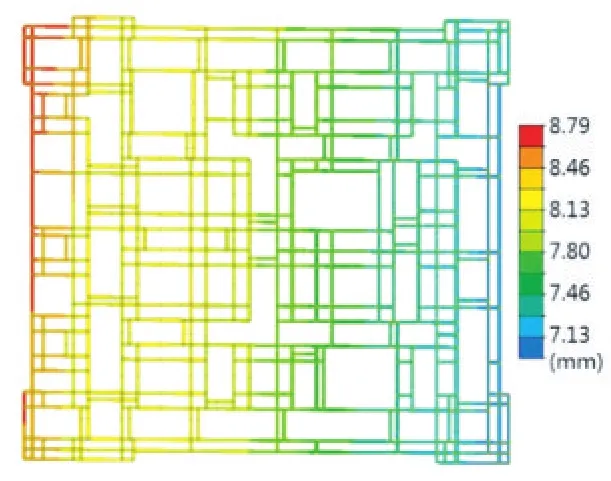
图13 钢平台提升状态Y向位移云图Fig.13 Y-direction displacement contour of the steel platform in lifting state
有限元分析结果说明钢平台在不同阶段的竖向荷载与作用下的受力及变形均符合相关要求,有效论证了钢平台体系设计阶段结构分析的合理性。
3 钢平台结构体系控制
本文钢平台体系安全控制是指在使用阶段为保证现场施工人员为保证钢平台体系及现场施工人员安全性所采取的措施,主要体现在两个方面,即荷载与作用、变形控制。
3.1 荷载作用
荷载与作用主要是指在使用阶段严格控制各部位、各阶段施工荷载,体现了对钢平台体系竖向变形的控制。
(1)正常工作状态:顶部平台限制值为7 kN/m2,为防止悬挑区域变形过大,特别针对悬挑区域顶层不允许堆载;F4~F6层限制值1.5 kN/m2;F1~F3层限制值1 kN/m2;外挂脚手架内外侧均为1 kN/m;最大施工荷载为钢筋自重,控制值为2 100 kN,并均匀分布。
(2)整体提升状态:顶部平台取0.5 kN/m2;F1~F6层取0.5 kN/m2;外挂脚手架内外侧均为1 kN/m;无钢筋堆载。
(3)实际施工中对钢平台进行变形测量,正常工作状态下中部区域变形小于10 mm,悬挑处变形也在30 mm以内,满足设计中钢平台体系竖向变形的控制要求。
3.2 变形控制
变形控制主要是为了控制使用阶段风荷载作用下钢平台体系在水平方向的变形,提高钢平台体系的整体稳定性。
(1)在钢平台内筒架与混凝土核心筒之间设置附墙滑轮,滑轮与钢平台之间通过强力弹簧顶紧,以抵抗水平风载的影响,实际水平变形小于计算值,结构水平向变形具备足够的安全储备。
(2)钢平台外架底部设有闸板,施工阶段闸板全部与剪力墙顶紧闭合,可以抵抗一定的水平风荷载影响。
4 现场安全监控
为结合实际工况对钢平台体系安全性进行分析和验证,现场采用实时自动监测装置对钢平台体系进行数据采集和安全监控。
4.1 仪器安装及测点布置
4.1.1 应变计安装
选取JTM-V5000F型振弦式表面应变计进行监测,应变计由中部测量模块与两端安装模块组成。安装时采用双组分胶或焊接方式将安装模块与钢结构表面进行牢固连接。安装完成后采用JTM-V10A智能型振弦式手持传感器读数仪进行安装检测及初始数据读取,读数正常则完成应变计安装。
4.1.2 数据采集设备
根据测点数量,采用配套的JTM-MV20A智能型振弦式传感器采集箱,内置两个采集模块,共计32通道,可满足测点布置需要。通过传输线将所有应变计与采集模块进行连接,数据即可传输并暂存于采集设备中,定期利用计算机进行数据读取。采集间隔设定为15 min。
4.1.3 测点布置
测试项目包括平台梁应变、钢平台立柱的应变。根据Midas计算结果选取受力较大堆载区域连续梁2根进行监测,每根工字钢梁分别在跨中和两端选取三个截面进行应变测试,每个截面的测点分别在上下翼缘各布置振弦式应变传感器一个,总计6个测点(12个应变监测点);悬挑梁在固支端部取靠近节点截面进行应变测试,选取悬挑梁4根进行监测,总计4个测点(8个应变监测点);钢立柱则是在三个立面各布置一个应变片,选择受力较大立柱2根进行监测,总计6个测点(6个应变监测点),总计采用振弦式表面应变计26个。测点平面布置如图14所示。为保证应变计在施工中免遭破坏,现场采用铁保护外壳及铁丝网进行防护,智能振弦式传感器采集箱布置于钢平台系统提升控制机房内,可最大程度免受外界干扰影响(图15)。

图14 测点布置平面图Fig.14 Layout plan of measuring points

图15 应变计现场安装及保护照片Fig.15 Installation and protection of strain gauges
4.2 监控数据分析
4.2.1 初始值确定
监测仪器安装时间为钢平台整体结构安装完成,各类小型设备、施工堆载及施工人员等活荷载未加载,仅有恒载作用时进行安装,尽可能将初始值“零点”固定为仅受恒荷载及常规风载作用下的数值,以此凸显施工过程中各类可变荷载对钢平台自身结构受力的影响,从而分析其各类工况下的安全性。
4.2.2 施工工况分析
监测仪器安装时间为钢平台整体结构安装完成,各类小型设备、施工堆载及施工人员等活荷载未加载,仅有恒载作用时进行安装,尽可能将初始值“零点”固定为仅受恒荷载及常规风载作用下的数值,以此凸显施工过程中各类可变荷载对钢平台自身结构受力的影响,从而分析其各类工况下的安全性。
4.2.3 数据转换
采用如下计算公式实现频率测量结果与应变的转换,并最终利用钢材弹性模量E计算得出测点钢结构所受应力:
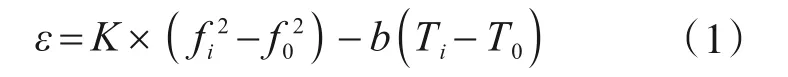
式中:ε为微应变变化值;K为应变计率定系数;fi为测量频率;f0为初始频率;b为温度修正值;Ti为测量温度;T0为初始温度。
4.3 监测结果
4.3.1 工况分析
钢平台体系结构分析和安全控制一般分为两个工况,即正常使用状态和整体提升状态。正常使用状态下,钢平台体系支承点为下部牛腿,传力路线为平台板→平台梁→钢立柱→底梁→牛腿→剪力墙,荷载除需考虑初始的结构自重、外挂脚手架荷载、风荷载外,还要考虑顶层堆载、施工人员等施工荷载;整体提升状态下,钢平台体系支承点为上部提升钢柱,主要传力路线为钢平台荷载(包含自重及堆载)→平台梁→爬升靴→爬升油缸→爬升钢柱→剪力墙,荷载仅考虑初始的结构自重、外挂脚手架荷载、风荷载及少量堆载。
4.3.2 结果分析
本文节选有代表性的标准层施工过程数据分别针对平台连续梁、悬挑梁、钢立柱进行分析,结果如下:
(1)平台连续梁监测结果分析
由图16、图17可知,平台连续梁中部监测点(下翼缘)随着施工工况的开始进入加载阶段,应力逐渐增大,并在36 MPa附近波动,较为符合实际施工中钢筋吊运至钢平台后不断消耗又不断补充的过程;进入提升工况后,钢平台连续梁中部(下翼缘)应力突然减小并进入负弯矩区间在-22 MPa附近波动,主要原因在于钢平台进入爬升阶段后逐步清理上部荷载,且测点附近存在爬升钢柱,提升时给予平台梁向上的力,带动平台爬升,其受力方向与施工工况相反。与有限元模模拟结果(活荷载作用下施工工况最大应力为38.8 MPa,提升工况最大应力为-10.4 MPa)相比,施工工况结果较为接近,提升工况也仅有较小的误差,考虑是提升过程中不均匀提升导致的应力增加。

图16 连续梁中部下翼缘应力变化图Fig.16 Stress variation of the lower flange in the middle of the continuous beam
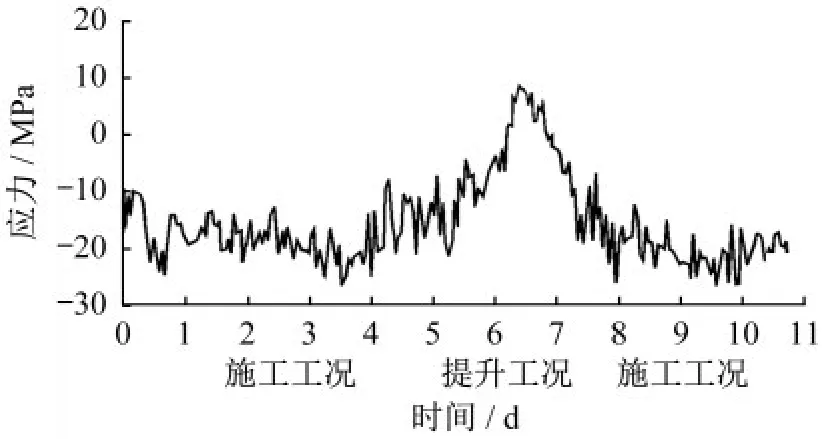
图17 连续梁中部上翼缘应力变化图Fig.17 Stress variation of the upper flange in the middle of the continuous beam
(2)平台悬臂梁监测结果分析
由图18、图19可知,平台悬壁梁端部监测点(上翼缘)随着施工工况的开始进入加载阶段,应力逐渐增大,并在130 MPa附近波动,且波动幅度较连续梁大(±20 MPa的波动),增长幅度较连续梁小(由100 MPa增长至130 MPa),体现了悬臂梁实际施工中对荷载较为敏感的特点及悬挑区域限制堆载的效果;进入提升工况后,钢平台悬壁梁端部(上翼缘)应力逐步减小,最小值约为60 MPa,主要原因在于测点附近存在爬升钢柱,进入提升工况后钢平台支点转换至爬升钢柱处,悬臂梁端部所受弯矩减小的缘故,但其弯矩符号未发生变化。与有限元模模拟结果(活荷载作用下施工工况最大应力为169 MPa,提升工况最大应力为54.2 MPa)相比,爬升工况结果较为接近,施工工况结果理论值较实际值大40 MPa左右,体现了实际施工中对悬挑区域着重采取禁止或限制堆载等安全措施的作用。
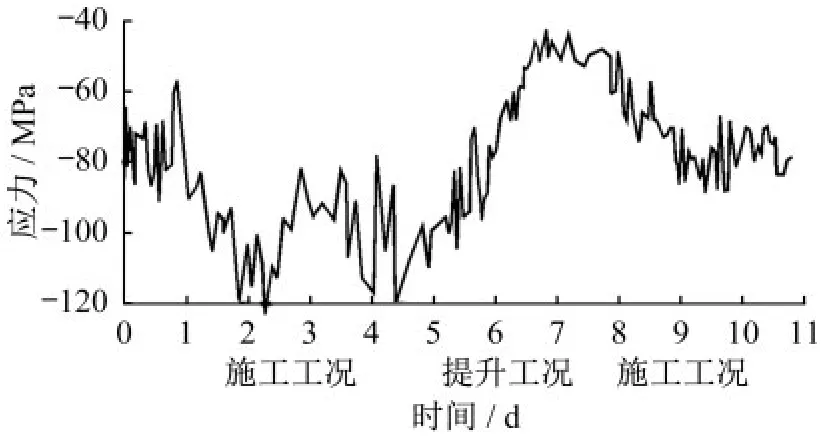
图18 悬臂梁端部下翼缘应力变化图Fig.18 Stress variation of the lower flange at the end of the cantilever beam

图19 悬臂梁端部上翼缘应力变化图Fig.19 Stress variation of the upper flange in the middle of the continuous beam
(3)钢立柱监测结果分析
由图20可知,平台钢立柱监测点(侧壁)在施工工况下立柱应力在-140 MPa下无规律波动,考虑是堆载及风荷载综合影响下的结果;在提升工况下立柱应力在20 MPa下无规律波动,比较符合提升过程中立柱受拉且荷载较小的特点,波动较大则可能是风荷载影响的结果。与有限元模模拟结果(活荷载作用下施工工况最大应力为-166 MPa,提升工况最大应力为26.4 MPa)相比,基本相同,误差可能由于风荷载的波动造成。
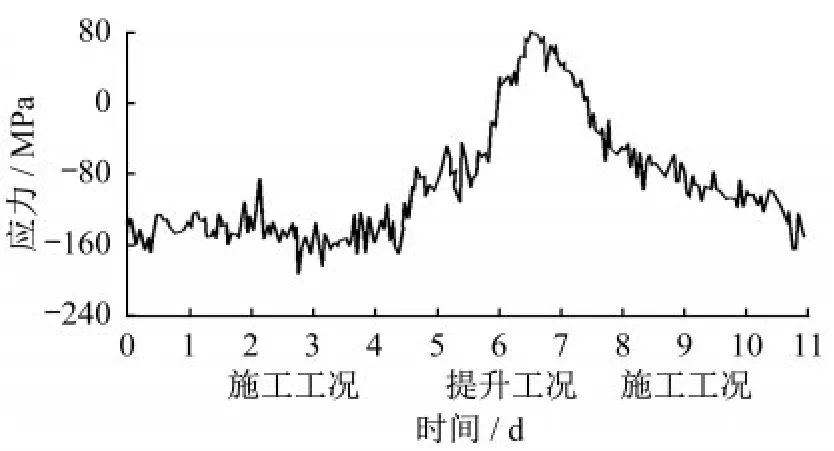
图20 平台立柱应力变化图Fig.20 Stress variation of the platform column
4.4 监测值与计算值比较
由上小节得到的连续梁中部上、下翼缘的测点应力变化图,悬臂梁端部上、下翼缘应力变化图和平台立柱应力变化图,提取一个标准层施工周期内这些测点处的应力最大值、最小值和平均值,并于计算得到的对应位置单元的应力值进行对比,结果如表2所示。

表2 应力的监测值与计算值对比Table 2 Comparison of measured and calculated values of stresses
结合监测结果与有限元分析,发现钢平台应力应变趋势与预想较为一致,且由于施工过程中安全控制措施的采用及设计计算中各类安全系数的加入,钢平台实际应力应变较计算结果整体偏小。
5 结 论
(1)通过监测应力与计算应力值的对比得出:平均监测应力是计算应力值的70%,顶升钢平台是安全可靠的;各监测杆件的实际受力与计算结果基本一致,验证了数值模型的合理性。
(2)有限元分析与现场监测都表明,在各工况下,活荷载对整体钢平台的受力和变形有较大影响,尤其是平台悬臂梁部位。建议钢平台顶部活荷载限值不能超过7 kN/m2。此外,野蛮施工、违规施工等各种不确定因素也会影响钢平台受力,因此还应规范施工现场的管理。
(3)对整体钢平台结构进行全过程理论分析,并根据受力特点布置了自动化监控装置,采集的监测数据与计算结果吻合性较好,有效控制了整体钢平台结构的安全性,为大型装备结构的风险控制提供了支撑。

