考虑不同固结阶段条件下旧桩承载力的预测研究

苏 聪 李镜培 ，* 谢 峰

（1.同济大学岩土及地下工程教育部重点实验室，上海 200092；2.同济大学地下建筑与工程系，上海 200092）

0 引 言

随着社会经济和城市建设快速发展，土地资源不断减少，越来越多的建筑需要在已有建筑拆除后的场地上建设。旧桩再利用不仅能使再建建筑物减少材料耗费，而且可以节省在原址上二次施工费用[1]。但旧桩与新桩相比，不仅在自身材料与力学特性上有很大差别，其桩周土及环境因素等亦有区别，这些区别导致了旧有桩基与新桩在承载力计算方面有着很大不同。

静压桩沉桩产生的超孔隙水压力会随时间逐渐消散，土体的有效应力与强度也会逐渐恢复与提高[2]。因此，相较于新桩，旧桩周围土体的力学特性发生了较大的变化，而在超孔隙水压力消散之后，土体还会发生以土体蠕变为主的次固结，这一过程也会造成土体孔隙比下降、强度与承载力增加，上述过程就是桩基承载力的时效性。

对于桩基承载力变化的计算可以分为理论解析解法和经验公式方法，这两种方法有着各自的优缺点。

首先是理论解析解，关于旧桩桩周土体的力学特性，Li等[2]基于K0-MCC修正剑桥模型以及圆孔扩张理论推导出了桩周土体应力以及孔压解答，该解答也被李林[3]用于推导静压桩时变承载力与沉桩终压力的理论关系。上述理论解析方法虽然可以解释承载力的变化机理，但是计算过程过于复杂，不便运用于工程实际中，同时理论解析解大多考虑的是沉桩结束后超孔隙水压力消散的主固结阶段，无法反映次固结阶段桩基承载力的变化。

在桩基承载力变化的经验公式解答方面，Skove和 Denver[4]、Tan 等[5]通过实测数据提出了基于短期承载力估算长期承载力的经验公式。但经验公式的准确性依赖于场地条件等诸多因素并且不能反映承载力变化的内在机理。

Komurka[6]通过总结大量试验数据，认为黏土中沉桩完成后，桩基承载力随时间的变化规律可大致分为三个阶段：第一阶段，在沉桩结束后较短的时间内，承载力增长幅度与时间对数呈对数关系；第二阶段，承载力增长幅度与时间对数呈近似直线关系；第三阶段，沉桩产生的超孔压基本消散，土体结构性变化、蠕变等效应引起桩承载力缓慢变化，其增长幅度与时间对数呈线性关系，该阶段即为次固结阶段。

关于次固结阶段桩基承载力的变化，尹振宇等[7]总结了软黏土蠕变研究的现状，讨论了一维、三轴、复杂应力条件下软土蠕变的特性。Liingaard等[8]提到了Bjerrum的经典时间等值线模型，认为在e-lgp坐标下不同时间的变形线是一系列相互平行的直线，即孔隙比随时间的变化与土体原应力状态无关。

针对上述研究中存在的问题，本文主要对旧桩承载力的时效性及其简化计算方法进行讨论。首先以承载力增长的机理不同将承载力的变化划分为主固结与次固结两个不同的阶段，并提出了可应用于工程实际的简化计算公式；最后通过奥西拉河试桩试验的数据，验证了本文简化计算理论的有效性。

1 主固结阶段承载力时效性

本文提出使用时效性系数来表现沉桩结束之后承载力的变化，定义时效性系数βt为沉桩后任意时刻桩基承载力与初始时刻承载力标准值的比值：

该定义下，任意时刻的桩基承载力Qt可以表示为

式中，承载力时效性系数βt采用本文提出的简化公式进行计算，对于不同的固结阶段，由于引起桩基承载力增加的主要机理不同，βt将采用不同的简化方法进行计算；Q0表示t0时刻承载力标准值，可以参考规范中的经验参数法以及静载试验法确定；Qt表示t时刻的桩基承载力。

1.1 主固结阶段承载力时效性的计算

对于主固结阶段承载力的时效性，已经有不少国内外学者进行过相关研究，相关研究主要可以分为经验公式法以及理论解析解法。

1.1.1 经验公式

关于主固结阶段桩基承载力时效性，最经典的经验公式是Skov和Denver[4]提出的半对数经验公式。Haque等[9]对静压桩时效性经验公式进行了总结，如表1所示。

表1 桩基承载力时效性经验公式（部分）[9]Table 1 Empirical calculation formula of time-dependent bearing capacity of driven pile（Part）[9]

以上经验公式虽然与实测数据有很好的吻合度，但也存在一些缺点：①经验公式是否准确在很大程度上依赖于试验场地的地质条件、施工方法及桩型；②经验公式忽略了静压桩承载力时效性的内在机理，无法反映静压桩承载力随时间变化的本质。

1.1.2 承载力与超孔隙水压力解析解

关于承载力时效性的理论推导，大部分研究结果以及实测数据都表明，主固结阶段承载力的时效性主要与超孔隙水压力的消散有关。李林等[3]基于圆孔扩张理论推导出的承载力时效性公式表明，桩侧与桩端阻力随时间的变化都与桩侧水平向有效应力的变化成正比，但是其关于孔隙水压力消散的解析解为无穷级数的形式，求解较为复杂，难以运用于工程实际计算中。

对于初始超孔隙水压力，本文采用的是南京工业大学宰金珉等[10]提出的计算公式，该公式不仅简洁，同时反映了超孔隙水压力在径向和沿深度方向的变化规律，克服了超孔隙水压力计算值在边界上的不连续，且计算结果与实测结果基本一致，其表达式为

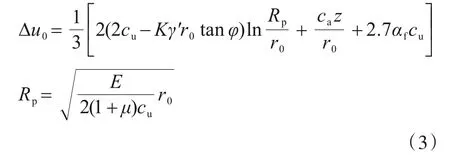
式中：Δu0为初始超孔隙水压力；Rp为塑性区半径；cu为土的不排水抗剪强度，K=tan2(45°+φ/2)，φ、ca为桩土界面的摩擦角、黏聚力；γ'为土体浮重度；r0为桩的半径；z为计算点的深度，αf=0.707(3Af-1)；Af为孔压系数；μ为土的泊松比；E为土体弹性模量。

1.2 经验公式参数拟合

Skove 和 Denver[4]通过实测数据提出了基于短期承载力估算长期承载力的经验公式Qt=Q0[Alg(t)+1]，但该经验公式中经验参数A的取值无法反应不同场地条件的差异性，因此本文对经验参数A的取值进行拟合，以提供更加精确的参数取值方法。宰金珉等[10]认为超孔隙水压力消散快慢主要与土体的水平向固结系数Ch以及桩径r0有关，Ng等[11]提出桩基承载力的变化与无量纲时间因子成正比。而主固结阶段桩基承载力的变化过程就是超孔隙水压力的消散过程，因此对于经验公式，参数A应当与水平向固结系数Ch以及桩径r0有关。所以假设经验参数是固结系数Ch以及桩径r0的函数。

本文选取了三个实例，分别来自于宰金珉等[10]，李林等[3]的试验结果。根据本文定义，承载力时效系数，将三个实例的承载力时效系数随时间的变化绘制在对数坐标系中，如图1所示。

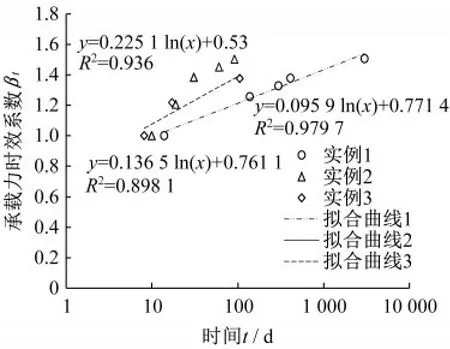
图1 实例拟合曲线（对数坐标）Fig.1 Fitting curve of examples（logarithmic coordinates）

式中，B为经验参数，根据实例数据拟合结果，参数B取值为0.4。

1.3 半理论半经验简化公式

根据李林等[3]的研究，任意时刻桩基承载力与初始时刻桩基承载力之比等于任意时刻桩基径向有效应力与初始时刻桩基径向有效应力之比：

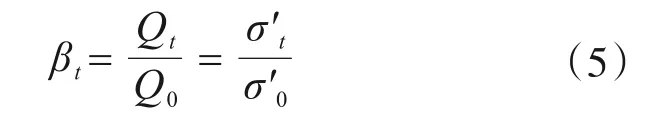
以下计算过程中，对于初始超孔隙水压力Δu0采用南京工业大学的理论解。对于超孔隙水压力的消散过程，为便于工程实际的应用，采用经验公式拟合方法，简化为对数衰减过程。

挤压力的求解参考姚笑青等[12]的计算方法：

ur·Af=Δu0，初始挤压力，则t时刻土侧向有效应力：

Δut的简化计算公式为

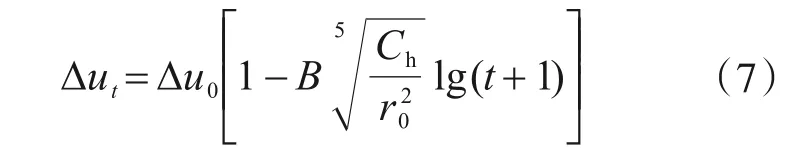
式中，B为经验参数，根据2.2节实例数据拟合结果取0.4。

在1.2节选取的三个实例中，通过半经验半理论公式计算得出的承载力时效系数与实测结果的对比如图2—图4所示。

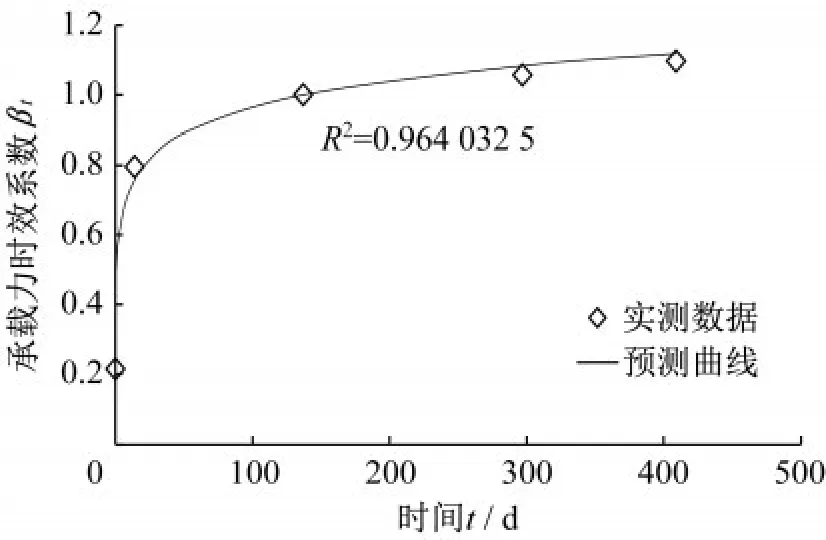
图2 实例一实测数据与预测曲线对比Fig.2 Comparison of measured data and predicted curve for example 1

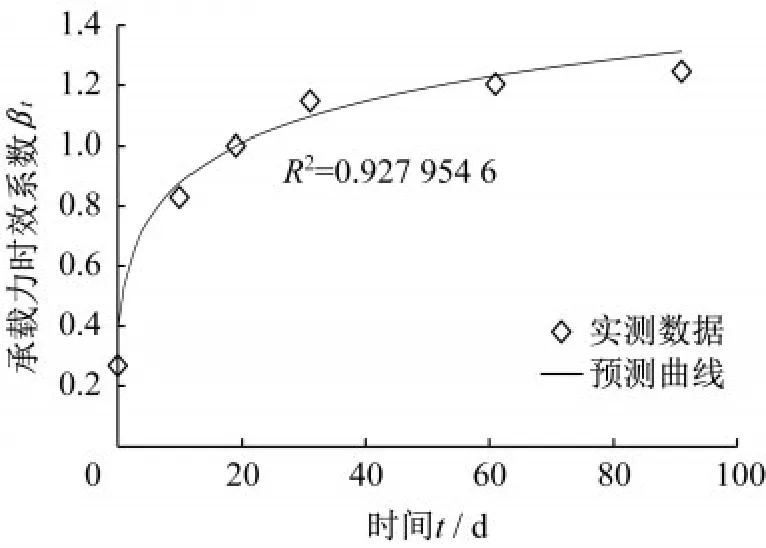
图3 实例二实测数据与预测曲线对比Fig.3 Comparison of measured data and predicted curve for example 2

图4 实例三实测数据与预测曲线对比Fig.4 Comparison of measured data and predicted curve for example 3

采用统计学中的决定系数R2对本节提出的半经验半理论公式的计算结果进行评价。决定系数R2又称测定系数、可决系数，是回归分析中说明因变量变化可靠程度的一个统计指标，其定义为

式中：yi为实测数据值为回归数据值为实测数据平均值。

为了避免出现负值，对简化公式进行线性变换，等效成为线性回归的形式，计算得出简化计算公式的线性回归R2值如表2所示。

表2 线性回归R2计算值Table 2 The coefficient of determination R2after linear regression

从表2计算结果可以看出，预测曲线线性回归后的相关决定系数均达到了0.8以上，决定系数越接近1，表明回归效果越好，本节提出的半理论半经验公式能够很好地反映实际承载力随时间的变化。

2 次固结阶段承载力时效性的计算

2.1 次固结阶段研究的重要性

众多研究与工程实例表明，沉桩完成后，桩周土的超孔隙水压力大多会在一个月内基本消散完毕，雷华阳等[13]在天津东疆保税港区二期工程中选取的实测结果表明，沉桩后20 d，绝大部分土层超孔隙水压力消散率在90%以上。Konrad等[14]也指出桩周土的超孔隙水压力在33 d左右完全消散，Roy等[15]指出超孔隙水压力的消散时间为20 d左右。

因此在讨论沉桩结束后桩基较长时间内的承载力变化时，对次固结阶段桩基承载力变化的计算也尤为重要。次固结阶段桩周土体中超孔隙水压力已基本消散完毕，土体强度变化主要由土颗粒蠕变引起，因此对次固结阶段桩基承载力的时效性计算将重点研究土体的孔隙比变化。

2.2 次固结阶段承载力时效系数简化计算公式

次固结阶段土体的变形主要由土颗粒蠕变引起。许多室内试验和现场量测的结果都表明，次固结程度大小随时间的变化在半对数坐标系上接近于一条直线。Liingaard等[8]按照Bjerrum的经典时间等值线模型给出了孔隙比随时间变化的表达式，如图5所示，从图中的时间等值线中可以看出，e-lgp坐标下不同时间的变形线是一系列相互平行的直线，意味着孔隙比的变化Δe与初始应力状态p0无关。

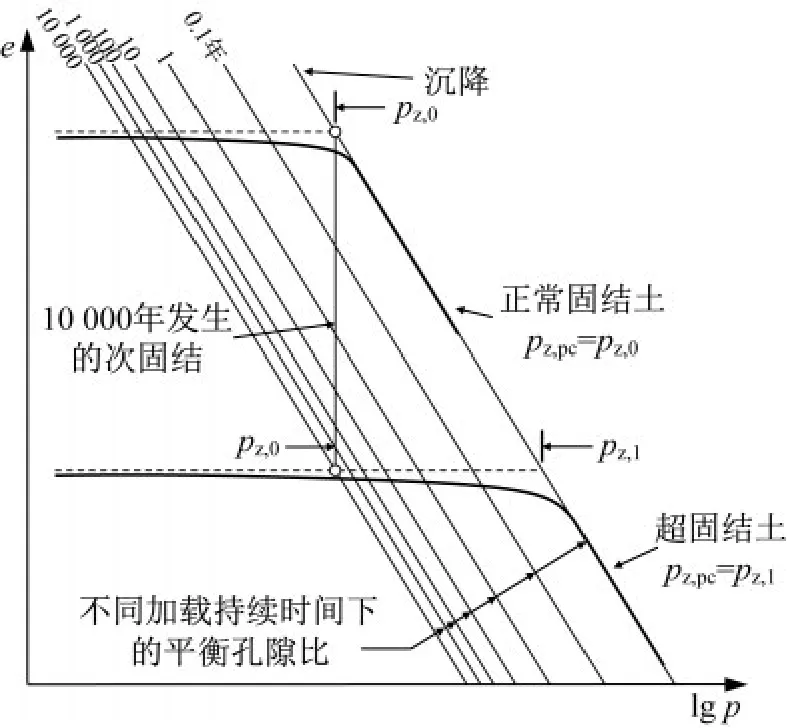
图5 时间等值线模型Fig.5 Bjerrum’s time contour model

Bjerrum经典理论[8]考虑的是一维固结下孔隙比的变化，其表达式为

式中，Cαe为次固结系数，与土体本身的应力状态有关。

2.3 次固结阶段简化公式实例验证

为验证简化式（12）的准确性，将简化公式计算结果与Augustesen等[16]实测数据中16.1号试桩的实测结果对比如图6所示。

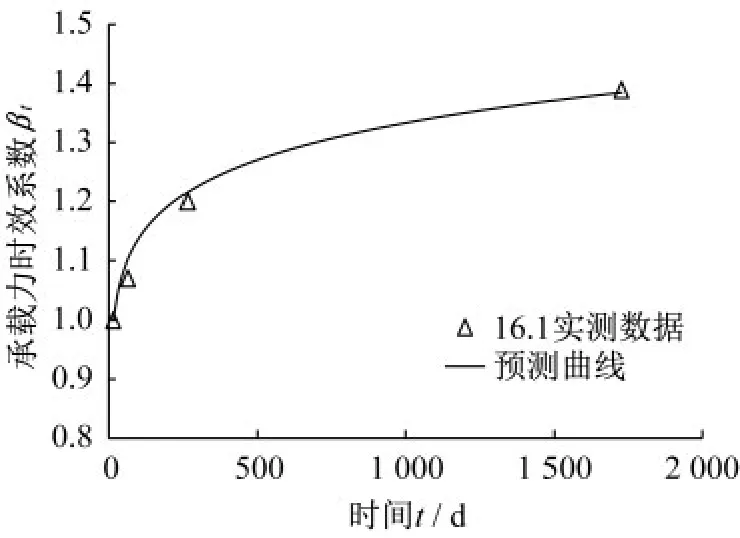
图6 实例16.1与预测曲线对比Fig.6 Comparison of measured data and predicted curve for example 16.1

从图6中可以看出，简化公式计算出的预测曲线与实测值之间有令人满意的吻合程度

简化公式中参数λ和κ的值比较固定，变动范围不大，对承载力时效系数计算结果的影响较小。2.4节将对次固结系数Cαe、初始时间t0对于简化公式（13）计算结果的影响进行讨论。

2.4 次固结阶简化计算公式参数分析

2.4.1 次固结系数

土体的次固结系数主要与土体的应力状态有关，但并不是简单的线性关系。胡建平等[17]对浙江平阳港区近海黏土的次固结系数进行了研究，图7为同一钻孔不同深度次固结系数与土体应力大小的关系。

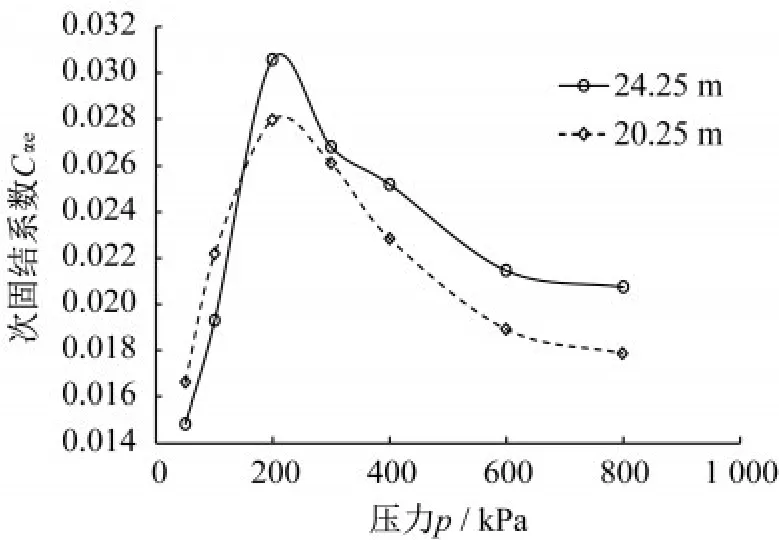
图7 不同深度处次固结系数与压力的关系（浙江沿海）Fig.7 Relationship between secondary consolidation coefficient and pressure at different depths（coastal area of Zhejiang Province）

从图7中可以看出，次固结系数的范围在0.01～0.07之间。结合其他相关文献研究成果，次固结系数大多在0.005～0.03的区间内。本文以0.004 为梯度，分别取Cαe=0.014，0.018，0.022，0.026，0.030，0.034，计算并绘出不同次固结系数下承载力时效系数βt与时间t之间的对数关系，如图8所示。

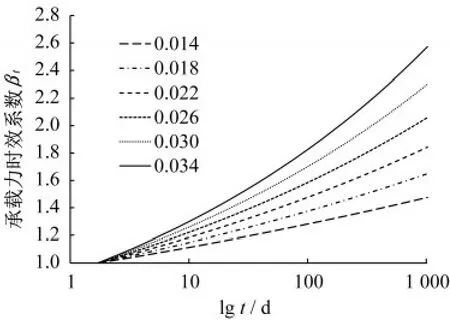
图8 承载力变化趋势随次固结系数的变化Fig.8 Trend of bearing capacity with secondary consolidation coefficient

从图8中可以看出次固结系数对于承载力时效系数βt的影响：次固结系数Cαe越大，βt-lgt曲线的斜率就越大，承载力时效系数随时间增长就越快。

结合图7以及图8的计算结果可知：当土体应力小于200 kPa时，随着土体应力增加，次固结系数增加，承载力时效系数随时间增长越快；当土体应力大于200 kPa时，随着土体应力增加，次固结系数减小，承载力时效系数随时间增长越慢。

2.4.2 初始时刻

为了进一步探究初始时刻t0选取对承载力时效系数计算的影响，在式（12）的基础上，加入时间调整系数Ψ来考虑初始时间的影响，修改后的公式：

即Δ1=Δ2⇒Ψ1=Ψ2，说明对于简化式（12），无须根据初始时刻选取的不同而对公式进行调整，初始Q0，t0取任意值，计算出的Qt都是一样的。因此，虽然初始时刻t0的取值不同会影响承载力增长比例βt的计算结果，但是不会影响最终计算的任意时刻承载力Qt的计算结果。

3 实例计算

本节将主固结和次固结阶段的简化计算公式结合，对桩基沉桩结束后较长时间内的承载力变化进行预测。选取Bullock等[18]在奥西拉河试桩的实测试验结果作为对比。奥西拉河试桩的试验周期跨度较长，实测数据从第0.98 d到1 727 d（4.73年），可以较好地反映桩基从主固结阶段到次固结阶段全过程的承载力变化。

使用简化公式对奥西拉河试桩主固结阶段桩基承载力时效系数进行计算时，土体参数参考第二节中的黏土参数，计算得出超孔隙水压力在91 d左右消散完毕，91 d之后的承载力时效系数使用第三节次固结阶段的简化公式进行计算，取t0=91。将第0.98 d时的承载力作为桩基承载力标准值，计算试桩各个时间点的承载力时效性系数，与简化公式计算结果对比如图9所示。

图9 奥西拉河试桩实测数据与预测曲线对比Fig.9 Comparison of measured data and predicted curve for the test pile in the Osceola River

从图9中可以看出，在t=0.98 d、2.97 d、16.1 d、65.1 d、265 d和1 727 d时，承载力时效系数βt分别为1、1.23、1.47、1.57、1.76和2.04，承载力分别为972 kN、1 197 kN、1 427 kN、1 528 kN、1 712 kN和1 982 kN，采用本文提出的简化公式计算得到的承载力时效系数预测值βt分别为1、1.11、1.34、1.59、1.79和2.04，承载力预测值分别为972 kN、1 080.26 kN、1 299.19 kN、1 545.23 kN、1 739 kN和1 981.28 kN，实例结果与预测公式的决定系数R2=0.952 181，非常接近1，表明用本文提出的简化计算方法对桩基承载力时效性进行预测有较好的吻合程度。

4 结论

（1）本文定义了承载力时效系数βt来计算承载力随时间的变化。根据已有研究成果将桩基承载力随时间的增长划分为主固结与次固结两个阶段。

（2）考虑主固结阶段承载力的变化主要由超孔隙水压力的消散引起。提出了将解析解与经验公式模拟消散过程相结合的半经验半理论简化计算公式，用R2对公式的拟合精度进行了初步评价。

（3）考虑次固结阶段承载力变化主要由土体蠕变引起，采用了经典的一维固结理论对次固结阶段孔隙比的变化进行模拟，得到了次固结阶段承载力的简化计算公式，综合相关文献试验的实测数据对公式进行了验证。

（4）本文利用奥西拉河的试桩数据进行验证，将主固结与次固结阶段的预测公式结合在一起，进行了承载力长周期变化的计算。对比结果表明本文提出的承载力变化简化计算公式可以比较合理地预测长期受荷桩的承载力变化，对工程实际中的计算有一定的参考价值。