基于破坏概率的大跨度柱面网架不规则结构风灾易损性分析

柴云霏 范存新

（苏州科技大学土木工程学院，苏州 215011）

0 引 言

风灾是一种突发性强、影响力大的自然灾害，对结构进行风灾易损性分析是结构进行灾害损失评估的关键环节[1-2]。结构的风灾易损性是指在不同强度等级的风力作用下，结构达到某种极限状态的概率，也可以理解为结构在风力作用下发生损伤的可能性。对结构进行风灾易损性的研究对评估分析结构的抗风性能、建立结构的抗风设计规范具有重要意义。目前，国内外关于灾害易损性的研究主要集中在地震易损性分析方面，对风灾易损性评估的研究成果相当有限。风灾易损性的研究方法主要有专家判断法、灾后调查法和理论分析法。其中理论分析法成本低、费时少、分析结果较准确，具有一定的前瞻性，有着广阔的发展空间。

大跨柱面网架结构是一种典型的风灾易损结构，这类结构因强风而遭受损失和破坏的情况屡见不鲜。为了降低风灾带来的损失，有必要对大跨柱面网架结构进行风灾易损性评估，依据评估结果进行减灾救灾措施。

柱面网架的结构形式相对比较复杂，并且表现出一定的材料非线性和几何非线性，再加上柱面网架无法通过顶部位移角来定义结构的破坏状态[3]，在风灾易损性分析上存在一定难度，目前尚未看到相关的研究成果。本文以山西某大跨柱面网架不规则结构为例，提出风灾易损性的概率分析的实施流程，建立该类结构风灾易损性的研究方法——通过MATLAB软件模拟脉动风速，再由ANSYS有限元软件进行动力时程非线性分析，得到模拟结果后利用结构损伤指数的定义，来进行结构易损性的概率分析，计算出结构在不同风速作用下反应超过某种破坏状态的条件概率，根据计算结果绘制结构在0°和90°风向角下的易损性曲线。

1 大跨钢结构网架模型建立

1.1 工程概况和结构外形

本文所研究的储煤棚位于山西省大同市，该地区山地居多，且干寒多风，温差较大，有必要对该地的结构进行风振响应分析的研究。该储煤棚的结构分布形式为三心圆柱面网架形式，平面尺寸为178 m×636 m，高50.5 m，结构模型如图1所示。

图1 网架模型示意图Fig.1 Schematic diagram of grid model

网架结构采用正放四角锥体系，这种布置方式受力均匀、空间刚度大，并且制作安装方便。该三心圆柱面网架结构选取了上下弦双排支撑方式。目前，国内110 m左右跨度的网架结构通常采用单排对边支撑。但是对于风荷载影响较大、跨度也大于110 m的网架结构，拥有更好刚度的上下弦双排支撑可以使网架结构获得更好的稳定性和安全性。网架结构的端部开敞，内部放有煤堆，结构的跨度大且阻尼小，相对于地震作用，风荷载对于钢结构的应力将起到控制作用[4]，因此，对结构进行风振响应，研究结构的抗风性能相当重要。

1.2 结构ANSYS有限元模型的建立

本文中所用到的有限元模型首先利用3D3S软件，按照结构的实际分布绘图，作为过渡导入到有限元分析ANSYS软件中，根据实际情况对ANSYS模型进行微调，得到可以用于后续分析计算的结构模型。

模型中的所有杆件均采用圆形焊接钢管Q235钢，统一用三维空间梁单元Beam44和Beam188进行建模，杆件直径为φ22（0.110 5 m）与φ24（0.122 5 m）。整个模型共有节点8 741个，杆件29 952根，结构采用铰接，支座类型为三向固定支座。该模型中杆件材料的弹性模量为2.06×1 011 Pa，泊松比为0.3，热膨胀系数1.2×10-5，屈服极限235 MPa。

2 风荷载的模拟

在研究过程中，对于施加在结构上的风荷载的模拟，采用的方法主要可以概括为：

（1）通过MATLAB程序编制对应算法进行不同坐标点脉动风速的模拟，选取结构表面528个节点作为代表节点，输入节点坐标，模拟其在不同平均风速下的脉动风速数值。

（2）利用风速-风压公式将脉动风速时程转换成基本风压时程，再乘以风压系数得到结构最终的风压时程。

（3）计算每个节点的等效受力面积，将风压转换为施加在节点上的力。

（4）将计算出的节点力通过APDL参数化设计语言导入ANSYS有限元软件，用于进行后续的分析计算。

2.1 线性滤波法模拟脉动风速

线性滤波法又名AR法或是自回归法，它是风速时程模拟的经典方法之一，其主要思路是将随机过程抽象成均值为0的白噪声随机数，经过适当变化后拟合出具有指定频谱特性的时域模型。线性滤波法利用前几个时刻的脉动量生成下一时刻的脉动量，考虑到了一定的时间相关性，是计算效率较高的方法，且此法优点明显，计算简便、占用内存小、模拟速度快，既适用于线性结构也适用于非线性的结构。综上，本文采取线性滤波法进行脉动风速的模拟。

根据《建筑结构荷载设计规范》中的规定与结构所在地的现状，脉动风速模拟的主要参数如表1所示。

表1 风速模拟主要参数Table 1 Main parameters of wind speed simulation

考虑时间相关性生成的人工风速时程，通过与目标谱对比验证程序的合理性，图2是结构中1 236节点（坐标28，48.63，45.709）的模拟脉动风速时程曲线和模拟功率谱和目标功率谱的对比曲线。由图可知，模拟谱和目标谱基本吻合，此法具有较好的精度。

图2 1236号节点的模拟风速和模拟功率谱Fig.2 Simulated wind speed and simulated power spectrum at node 1236

2.2 结构风荷载分区及风压系数的确定

在本文的研究中，在通过查阅资料[4-8]，进行多项对比之后，最终确定以《火力发电厂土建结构设计规程》[6]中关于干煤棚的风荷载体型系数作为分区施加风荷载的理论依据，得到不同风向角之下各个分区的风荷载体型系数，通过公式确定不同荷载点的风压时程曲线，最后将各测点的风荷载时程数据施加在分区面积范围内的有限元模型节点上，在此过程中，结构体型系数的分区如图3所示，风压系数取值如表2所示。

图3 结构体型系数分区Fig.3 Structure coefficient partition

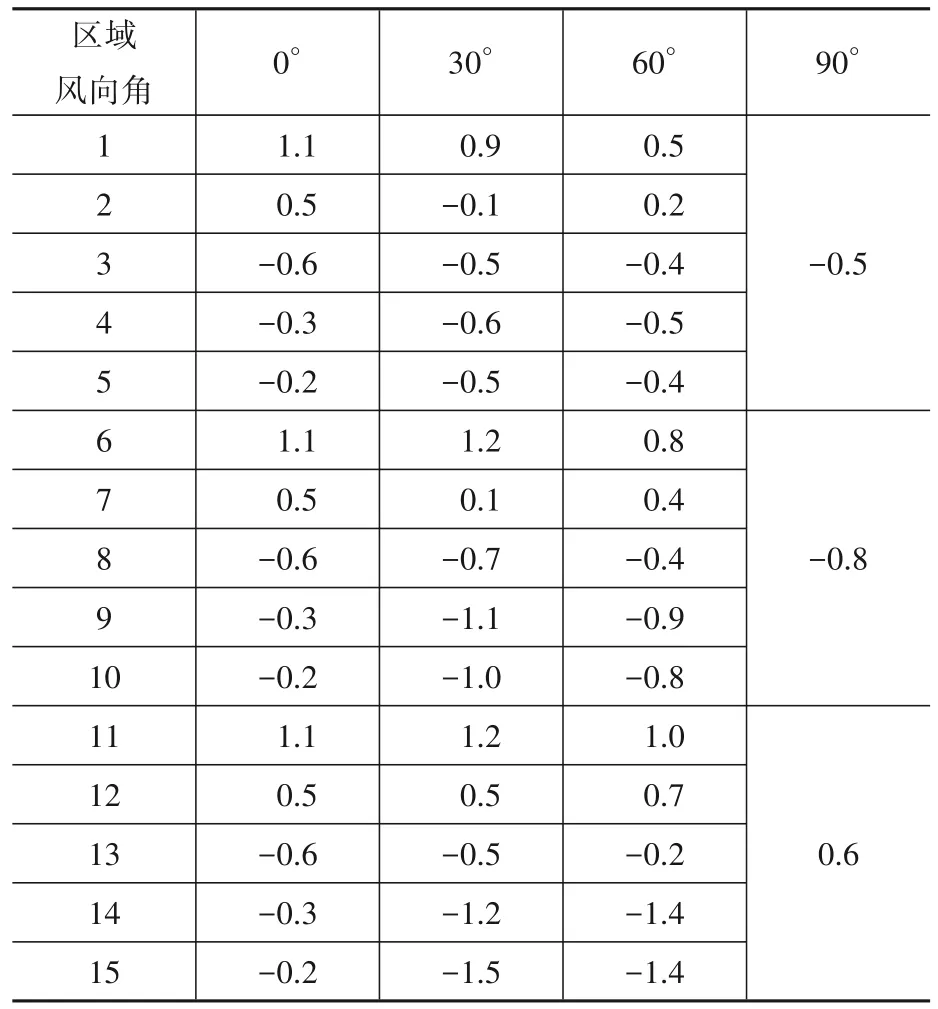
表2 《火力发电厂土建结构设计规程》中风荷载体型系数Table 2 Wind load carrier type coefficients in the“code for design of civil structures of thermal power plants”

在进行研究之前，首先规定：沿结构长边的方向为结构的X方向；沿结构跨度方向为结构的Y方向；沿结构高度方向为结构的Z方向。在风荷载的施加过程中，从坐标零点出发，以沿X方向正方向为0°风向角，沿Y方向负方向为90°风向角。

3 风灾易损性曲线的建立

3.1 分析步骤

本文考虑结构模型在0°和90°风向角下的风荷载效应，风速选取范围为平均风速10～80 m/s之间，共模拟15个不同的风速下的非线性动力分析，计算不同风速下结构构件不同破坏状态发生的概率并绘制风灾易损性曲线，具体步骤如下：

（1）利用ANSYS软件对结构进行不同风速下的非线性动力时程分析，得到一系列的结构响应数据，用于下一步的统计分析。

（2）对得到的数据进行回归分析，构建风速大小与结构反应的函数关系式，计算与每一种破坏状态对应的破坏概率。

（3）以风速为横坐标，不同破坏状态发生的概率为纵坐标、绘制风灾易损性曲线。

（4）根据绘制出的曲线，对结构在不同风速下的破坏状态进行评估。

3.2 结构损伤模型定义

20世纪60年代，损伤值是采用延性比来定义的，延性比越大则抗风能力越好，反之则越差，延性比通常可以用转角、曲率、位移来进行定义，相关公式如下：

采用延性比的方法虽然计算简便，但由于未考虑循环荷载对结构的影响，在使用上存在一定的局限性。1988年，Powell[9]在此基础上进行了改进，通过结构的弹性极限来对结构的破坏与否进行判断，公式如下：

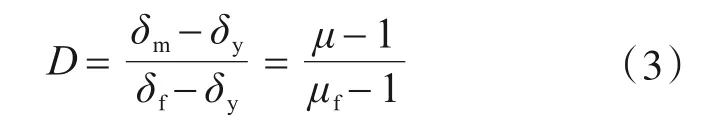
式中：δf为构件或结构的最大位移角；δy为其屈服时的位移角；δm为实际的最大位移角。

2017年，周静海等[10]提出通过构件的最大位移角来表示结构损伤，在考虑结构破坏结果的同时也考虑进了破坏过程中的损伤积累，公式表达为

在此基础上，本文将选用通过最大位移值来表示结构受到的损伤，具体公式表达如下：

式中：Xf为构件或结构的最大位移；Xy为其屈服时的位移；Xm为实际最大位移。

4.3 钢结构损伤划分

在研究过程中，选取整体损伤指数I作为反应结构破坏状态的指标，I的取值范围为0～1之间，数值越大，代表结构受到的损伤越严重，公式表达如下：

钢结构不同破坏状态对应的整体损伤指数如表3所示。

表3 不同破坏状态对应的整体损伤指数Table 3 The overall damage index corresponding to different failure states

3.3 易损性分析

对数据进行统计处理，通过式（5）和式（6）分别得到结构不同构件的损伤值和结构的整体损伤值。利用Origin软件绘制90°和0°风向角下风速v和不同风速对应的整体损伤指数I的散点图，如图4、图5所示。

图4 90°风向角下v和I的对数散点图Fig.4 Scatter plot of ln（v）and ln（I）under 90°wind direction

图5 0°风向角下v和I的对数散点图Fig.5 Scatter plot of ln（v）and ln（I）under 0°wind direction

对图中的数据进行拟合处理，可以得到90°风向角下风速和损伤指数的关系如式（7）所示，0°风向角下风速和损伤指数的关系如和式（8）所示：

假设结构的反应概率函数服从对数正态分布函数，可以用反映概率函数γ和能力参数概率函数α来反映结构易损性，即

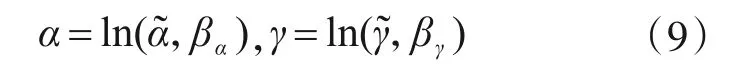
结构易损性其实是指结构在不同强度等级的荷载作用下结构发生不同破坏的概率，也就是结构动力响应超过结构抵抗能力的条件概率，用公式表示即为

结构反应γ和结构能力α服从对数正态函数的分布，所以结构发生破坏的失效概率可以表示为

将式（7）与式（8）代入式（11），即可得到两个风向角下结构不同破坏状态的超越概率。其中：结构反应概率函数γ通过整体损伤指数I得到，结构能力参数概率函数α查询相关规范[12]得到；的数值大小钢结构可以直接取值0.4。

计算结果如表4、表5所示。

表4 90°风向角下不同破坏状态的超越概率Table 4 Transcendence probability of different failure states under 90°wind direction

表5 0°风向角下不同破坏状态的超越概率Table 5 Transcendence probability of different failure states under 90°wind direction

根据所得数据，分别绘制以风速为横坐标、不同破坏状态的超越概率为纵坐标的易损性曲线，曲线图如图6、图7所示。

图6 90°风向角下的风灾易损性曲线Fig.6 wind disaster vulnerability curve under 90°wind direction

图7 0°风向角下的风灾易损性曲线Fig.7 wind disaster vulnerability curve under 0°wind direction

从表4和图6中可以看出，在90°风向角下，当风速达到40 m/s时，结构发生轻微破坏的概率达到50%；当风速达到50 m/s时，结构发生轻微破坏的概率达到75%，发生中等破坏的概率为33%，发生严重破坏和倒塌破坏的概率分别在11%和4%。结构在风荷载作用下具有较强的抗倒塌能力，发生轻微破坏和中等破坏的概率随着风速的增加有明显增大，发生严重破坏和倒塌的概率也随着风速的增加有一定幅度的增大。

从表5和图7中可以看出，0°风向角下的风灾易损性曲线形状和90°风向角下的曲线形状大致相似，但是在数值上前者要明显低于后者。当风速达到50 m/s时，结构发生轻微破坏的概率仅达20%，发生严重破坏和倒塌的概率更是微乎其微。结构发生轻微破坏和中等破坏的概率随着风速的增加有一定幅度的增大，发生严重破坏和倒塌的概率仅随着风速的增加略有增大。

4 结论

本文采用了基于破坏概率的研究方法对山西某大跨度柱面网架结构进行有限元数值模拟，根据模拟结果的统计分析绘制风灾易损性曲线，通过对风灾易损性曲线的分析可以得到以下结论：

（1）随着作用在结构上荷载的增大，结构的动力响应增大，发生不同破坏的概率也随之增大；在相同的风速下，结构发生轻微破坏的概率最大，发生中等破坏、严重破坏和倒塌的概率依次减小。

（2）本文研究的结构有着较强的抗倒塌能力，但是在强风作用下各类破坏的发生概率仍然不容小觑，在抗风设计中应该引起足够重视。

（3）在相同的风速等级下，结构在90°风向角下发生特定破坏的概率显然比在0°风向角下的概率更大；随着风速的增加，结构在90°风向角下的破坏概率的变化幅度同样更加明显。