Production of p-rich nuclei with Z =20-25 based on radioactive ion beams
Bing Li · Na Tang · Yu-Hai Zhang · Feng-Shou Zhang,3
Abstract Within the framework of isospin-dependent Boltzmann-Langevin model, the production cross sections of proton-rich nuclei with Z =20-25 are investigated.According to the reaction results for different isospin of projectiles 48Ni, 49Ni,and 50Ni,proton-rich fragments tend to be more easily produced in reactions with the protonrich projectile 48Ni. The production cross sections of the unknown nuclei in the vicinity of the projectile are sensitive to incident energy. It is observed that incident energy of 345 MeV/u is appropriate for producing proton-rich nuclei with Z =20-25. In projectile fragmentation reactions based on the radioactive ion beam of 48Ni at 345 MeV/u,several unknown proton-rich nuclei near the proton drip line are generated in the simulations. All these new nuclei are near-projectile elements near Z =28. The production cross sections of the new nuclei 34Ca, 37,38Sc, 38Ti,40,41,42V, 40,41Cr,and 42,43,44,45Mn are in the range of 10-2–102 mb. Hence, projectile fragmentation of radioactive ion beams of Ni is a potential method for generating new proton-rich nuclei with Z =20-25.
Keywords Production cross sections · Radioactive ion beams · Isospin-dependent Boltzmann-Langevin model
1 Introduction
The production of new exotic isotopes and determination of drip lines are frontier topics in nuclear physics[1–6]. To date, 3327 nuclides have been experimentally observed [7]. Erler et al. predicted the presence of approximately 7000 nuclides; therefore, more than half of these nuclides remain undiscovered [1,8].Investigation of exotic isotopes provides valuable information for understanding the processes of nuclear astrophysics and nuclear structure [9–12]. Moreover, this types of nuclear reactions provide further information on isospin dependent nucleon–nucleon interactions, offering a powerful method to study the nuclear equation of state and even the symmetry energy, which is important for the physics of neutron stars and supernovas [13–18].
To date,the proton drip line experimentally reached the medium-mass region, whereas the neutron drip line has only recently been detected up to Z = 10 [8, 19, 20]. The proton drip line is closer to the stable region because of the Coulomb repulsion between protons,which leads to a long lifetime even for nuclides outside the proton drip line[21].This results in shallow regions or sandbanks, which serve to bridge gaps of unbound nuclei along the path of the astrophysical rapid-proton capture (rp) process [22].Additionally, approximately 200 proton unbound nuclides remain to be discovered [8]. Some of these nuclides are reconstructed through their decay products,and some even have lifetimes long enough to be experimentally observable. With the establishment of sophisticated facilities,radioactive ion beams(RIBs)of nuclei with large excesses of neutrons or protons allow a deeper investigation of exotic isotopes, which has led to new discoveries such as halo nuclei and the change of magic numbers with isospin[23–26]. The separation and identification of exotic nuclei have become principally possible using two techniques:isotope separation online (ISOL) and in-flight separation techniques [27–32]. In particular, the cross sections of intermediate mass fragments under projectile fragmentation reactions at 140 MeV/u were investigated at the National Superconducting Cyclotron Laboratory(NSCL)at Michigan State University (MSU) using an A1900 fragment separator [4]. Recently, the proton-rich isotope68Br was discovered in secondary fragmentation reactions at the RIKEN Nishina Center in 2019, suggesting that secondary fragmentation reactions offer an alternative way to search for new isotopes[21].Similar experimental and theoretical studies have been conducted [33–39].
Exotic nuclei can be generated via projectile fragmentation, fission, and spallation [2, 40, 41]. Spallation is an effective reaction mechanism for the production of exotic nuclei for time-of-flight particle identification [42–44].High-energy projectile fission is appropriate for light and heavy fission fragments [45–47]. Projectile fragmentation is a common reaction mechanism that has recently been used to study the production of new exotic nuclei, and many new nuclides have been discovered [48–52].Recently, multinucleon transfer in peripheral reactions at beam energies from the Coulomb barrier to the Fermi energy has been considered to exhibit the potential of producing exotic nuclei because the projectile can pick up neutrons from the neutron-rich target [53–57].
The development of projectile fragmentation for producing new radioactive nuclides has led to a new era, not only in the discovery of new nuclides, but also in the generation and utilization of unstable RIBs. Models describing projectile fragmentation reactions deliver important inputs for yield predictions that are useful for planning experiments and future accelerator facilities [58].The models include Boltzmann-Uehling-Uhlenbeck(BUU)model [59–61], quantum molecular dynamics (QMD)model [62–66], the stochastic mean-field approach (SMF)[14, 67, 68], the abrasion–ablation (AA) model [69–71],the empirical parameterization of fragmentation cross sections (EPAX) [72–74], and the FRACS parameterization [75–77]. Transport models are good event generators and exhibit applications,for example,to design or simulate new detectors, and empirical approaches also provide better agreement with the experimental data within a large range of incident energy [78, 79]. For a thorough review,refer to Refs. [80–85]. The theoretical method applied in this study was developed by adding the fluctuating collision term to the BUU equation and introducing the isospin effect, which is the isospin-dependent Boltzmann-Langevin equation (IBLE) [86–95].
In this study, we investigate the production cross sections of nuclei near the proton drip line with charge number Z =20-25 by using RIBs in an isospin-dependent Boltzmann-Langevin approach. A good description of the experimental data with the IBLE model suggests the possibility of using the present theoretical framework for the prediction of exotic nuclei using RIBs, which will soon be available in upcoming facilities [8, 21, 35, 54]. The remainder of this paper is organized as follows. A brief introduction to the IBLE model is provided in Sect.2.The model test,calculation results,and discussion are presented in Sect. 3. Finally, the conclusions of the study are presented in Sect. 4.
2 Theoretical descriptions
In the IBLE model,the transport equation of motion for fluctuating single-particle density ^f(r,p,t) can be expressed in the following form [87–89, 93]:

Here, the ^fi=^f(ri,pi,t) denotes the diagonal elements of single particle density and W(12; 34)denotes the transition rate, which is related to the cross section of the corresponding two-body scattering process. δK(r,p,t) is the fluctuating collision term, whose second moment is characterized by a correlation function

where〈···〉presents the average over the local ensemble of BLE events, which is the local average [87–89, 93]. The fluctuating collision term acts as a stochastic force acting on ^f, which is consistent with the ‘‘fluctuation–dissipation theorem.’’The correlation function C(p1,p2)is assumed as local in space and time, and it is coherent with the Markovian treatment of the Boltzmann collision term[88,96].In the semi-classical limit,the correlation function is determined by the local averaged single-particle density f(r,p,t) as detailed in Ref. [88].
To obtain approximate solutions of the IBLE transport equation, a projection method was introduced and applied[86,92].The fluctuations were projected onto a set of loworder multipole moments of the momentum distribution.The zero-order multipole moment is constant along with the first multipole moment because of mass conservation and momentum conservation. The quadrupole moment of the momentum distribution exhibits a strong dissipative phenomenon,and it can describe the fluctuations very well.The propagation of fluctuations in the quadrupole moment of the momentum distribution alone does not provide a detailed description of the momentum space fluctuations.Thus, the octupole moment of the momentum distribution is also introduced, although its dissipative effect is not evident.We expect that such an approximation can provide a reasonable description of the gross properties of the dynamics of density fluctuations in heavy-ion collisions[86]. The local multipole moments of the momentum distribution are defined as follows:


where γs = 0.5 and 2.0 correspond to the soft and hard symmetry energies,respectively[94].The coefficient value of Csym was 29.4 MeV. The details on the symmetry energy are provided in Ref. [94, 95].
The cross sections of each channel used in the IBLE model are experimental parameterizations, which are isospin-dependent[97–99].Additionally,the in-medium cross sections for each channel were used in the model as detailed in Ref. [94]. In this study, we construct clusters using the coalescence model, in which parameters R0and P0are set as 3.5 fm and 300 MeV/c, respectively [95].Calculations were performed with 20 test particles, and simulations were conducted for 10,000 events,with impact parameter values ranging from 0 to 7 fm. The excitation energy of the produced light fragments is not sufficient to evaporate neutrons; therefore, the difference between the cross sections before and after de-excitation is small. In this study, we focus on the production cross sections of light fragments around Z =20.
3 Results and discussion

Fig. 1 (Color online) The cross sections presented as isotope distributions for 19 ≤Z ≤24 elements in 58Ni+9Be reaction at 140 MeV/u were stimulated via IBLE model for hard and soft symmetry energies and compared with the experimental data [4]
To test the feasibility of using the IBLE model to predict the production cross sections of nuclei in projectile fragmentation, we calculated the cross sections of nuclei with 19 ≤Z ≤24 in the reaction of58Ni+9Be at 140 MeV/u as shown in Fig. 1. The solid and dashed lines denote the results of the IBLE model for the hard and soft symmetry energies, respectively. The solid circles denote the experimental data obtained from Ref. [4]. As shown, the measured cross sections of the fragments are reasonably reproduced by the IBLE model for hard and soft symmetry energies. The peak locations of the calculated cross sections are close to those obtained via experiments. With respect to K and Ca, the peaks of the calculated cross sections overestimated the experimental value, and the difference was within one order of magnitude.The number of calculated isotopes is less than the experimental value,especially for fragments near the projectile, which is a limitation of dynamical simulations in IBLE, i.e., it is dependent on the number of simulated events. For the simulations of different symmetry energies, it is observed that the results are very close and differ only slightly in the proton-rich and neutron-rich regions. In the proton-rich region, more isotopes are calculated for soft symmetry energy than for hard symmetry energy. By comparing the two calculations with the experimental data, we observe that the IBLE model realizes a good description of the cross-section distributions but slightly underestimates the neutron-rich tails. The calculations for the soft symmetry energy produced more isotopes, especially for proton-rich nuclei.Therefore,it is reasonable to apply the IBLE model with soft symmetry energy to predict the production cross sections of proton-rich fragments in projectile fragmentation reactions.
Radioactive ion beams became possible with the development of large scientific installations worldwide[2, 21, 33]. To produce proton-rich nuclei with charge number Z ≈20, proton-rich beams should be used in projectile fragmentation reactions.48,49,50Ni are good candidates for radioactive beams because they exhibit small N/Z ratios near Z ≈20. They are most likely generated via projectile fragmentation in a newly built FRIB facility,such as the fragmentation of a58Ni beam on a beryllium target at an incident energy of several hundred MeV/u. To study the effect of isospin of the projectile on the fragments produced by projectile fragmentation, the isotopic distributions of fragments with Z =20-25 for the48Ni+9Be(circles),49Ni+9Be (squares), and50Ni+9Be (triangles)reactions at 140 MeV/u are shown in Fig. 2. Unknown nuclei are denoted by open symbols. The isospin Tzof projectiles48Ni,49Ni, and50Ni are -4, -7/2, and -3,respectively. It is observed that the produced fragments tend to be proton-rich because of proton-rich radioactive ion beams. In Fig. 2, several new nuclei near the proton drip line, such as37,38Sc,38Ti,40,41,42V,41Cr, and43,44,45Mn, are generated during simulations.The predicted production cross sections of these nuclei ranged from 10-2to 102mb. The number and cross sections of proton-rich new nuclei in the reaction with48Ni projectile are the highest, which is due to the highest absolute value of the projectile isospin and the lowest N/Z ratio. As the mass number of the projectile increases by 1, the peak of the isotopic distribution shifts to the right by approximately one unit, which shows a strong isospin effect in the projectile fragmentation reactions because the isospin effect is dependent on the density distribution of protons and neutrons. When the absolute value of the projectile isospin decreases or when the N/Z ratio increases, the produced fragments are closer to the stability line. The absolute values of isospins of newly produced nuclei are smaller than those of the projectile because as the reaction proceeds the isospin of the reaction system gradually tends toward equilibrium, which is the isospin diffusion process.
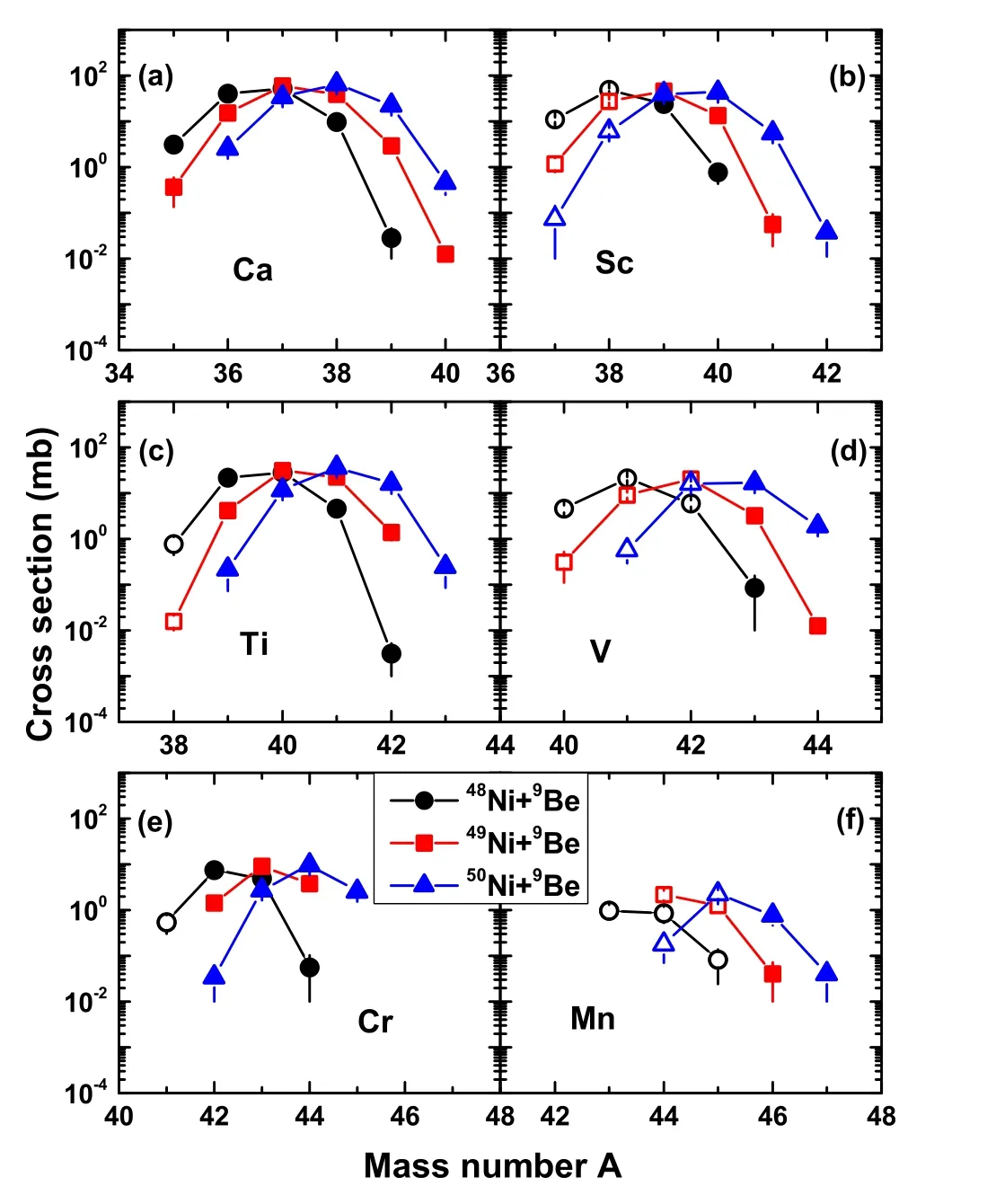
Fig. 2 (Color online) Calculated isotopic distributions of fragments with Z =20-25 for 48Ni+9Be, 49Ni+9Be, and 50Ni+9Be reactions at 140 MeV/u. Unknown nuclei are denoted by the open symbols
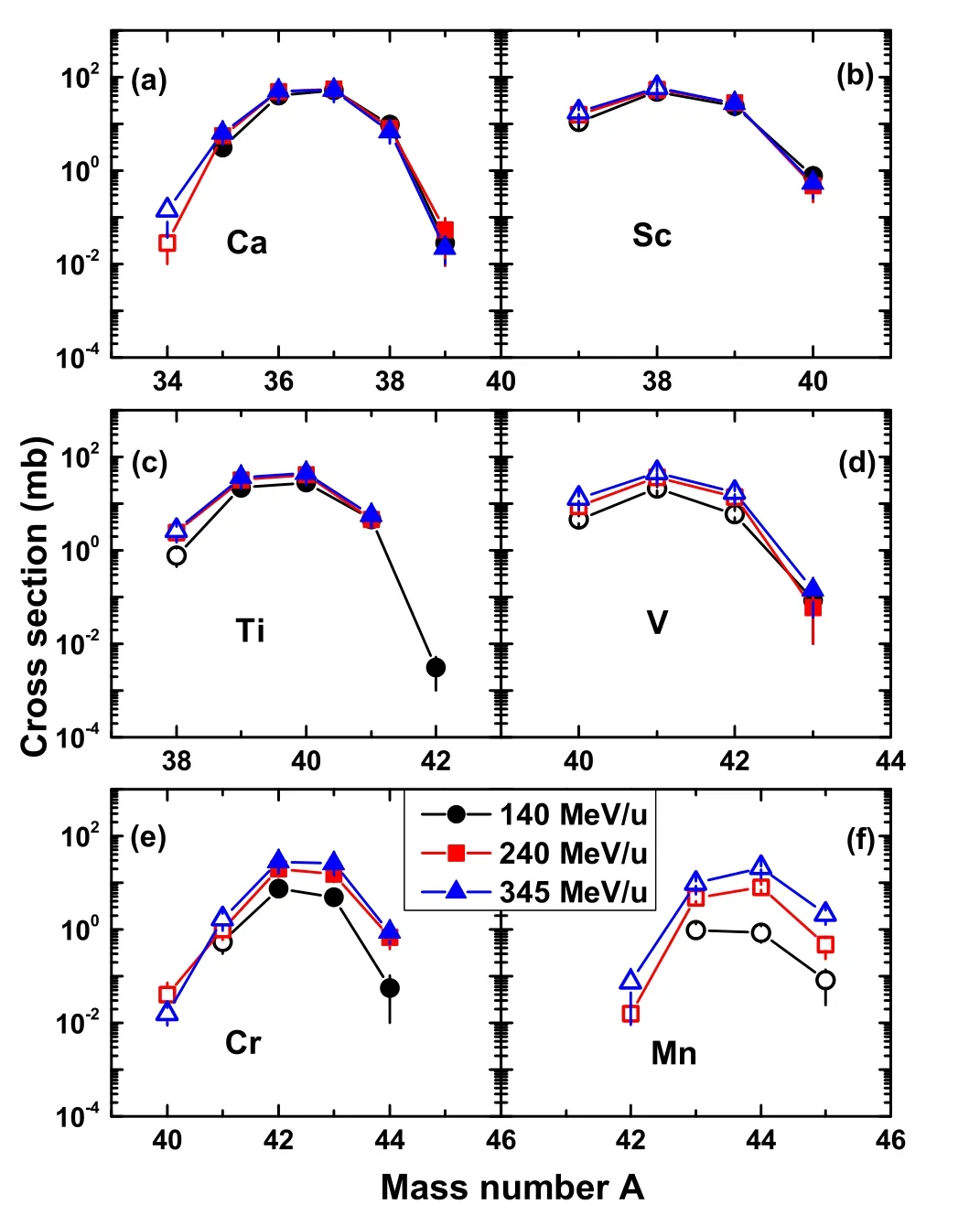
Fig. 3 (Color online) Calculated isotopic distributions of fragments with Z =20-25 for 48Ni+9Be at 140, 240, and 345 MeV/u.Unknown nuclei are denoted by the open symbols
According to the above results for different isospin of projectiles, reaction48Ni+9Be exhibits the advantage of producing rare proton-rich nuclei. To observe the incident energy effect, the production cross sections of the fragments in the48Ni+9Be reaction at 140 MeV/u (circles),240 MeV/u(squares),and 345 MeV/u(triangles)are shown in Fig. 3. As shown, the production cross sections of new nuclei at 345 MeV/u are the largest, especially the nuclei near the projectile. However, the difference among the results for different incident energies is not large. The discrepancy between the fragment cross sections at the three energies increased as the charge number of the generated fragments increased. Heavy fragments are mainly produced from peripheral collisions, which vary significantly with incident energies below 200 MeV/u [4].Additionally, the number of new nuclei produced in the simulations was consistent at incident energies of 240 and 345 MeV/u. In the48Ni+9Be reaction at 140 MeV/u, the production cross sections of the produced fragments with Z =20–25 decrease as charge number increases, whereas at 345 MeV/u, the production cross sections of the corresponding fragments do not show a significant decreasing trend. At 345 MeV/u, the projectile and target collide quickly with each other,resulting in fragments produced by the reaction. Furthermore, when compared to the reaction 140 MeV/u, the characteristics of the initial entrance channel are retained to the maximum extent at 345 MeV/u.
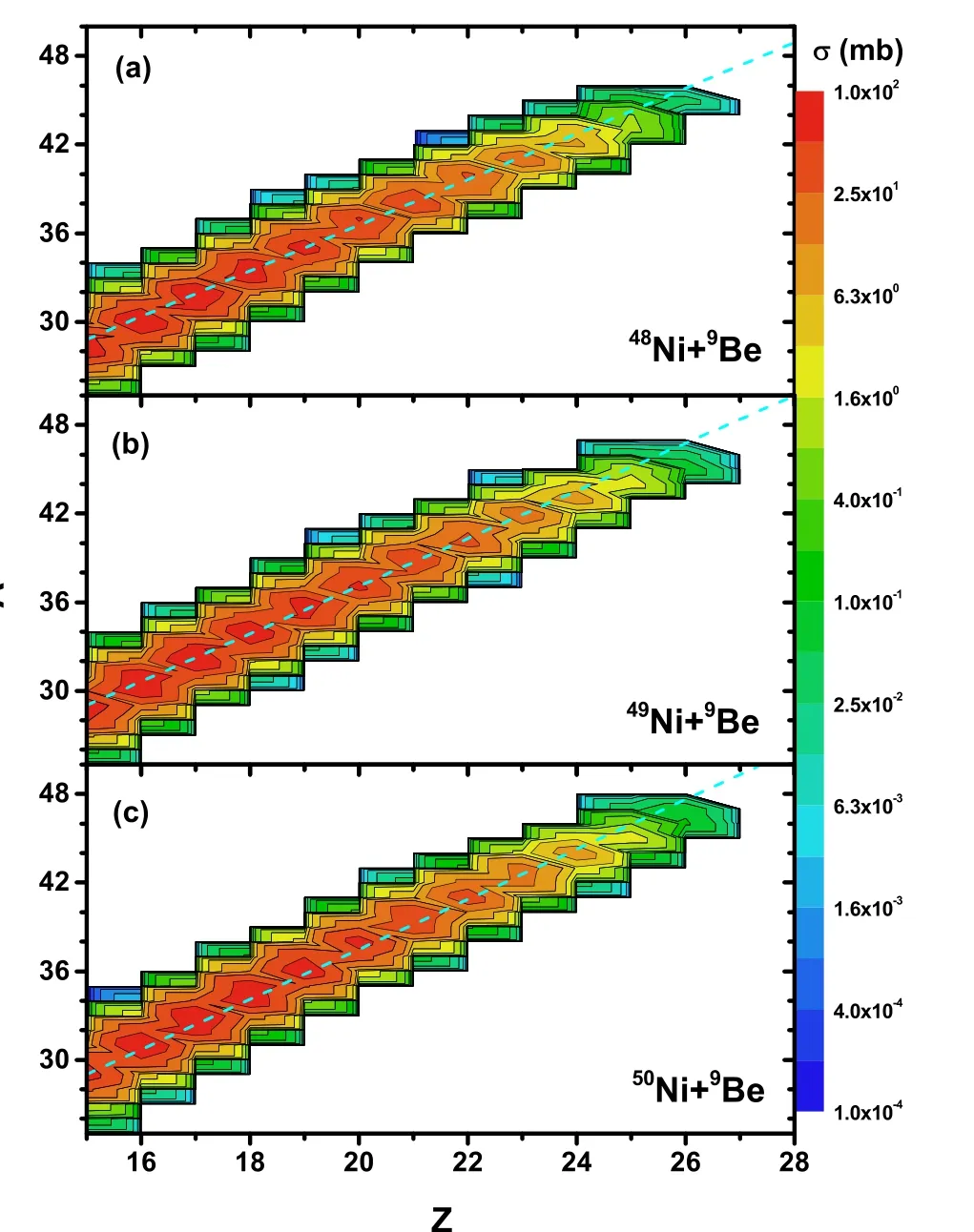
Fig.4 (Color online)Production cross sections as functions of Z and A for the fragments in 48Ni+9Be, 49Ni+9Be,and 50Ni+9Be reactions at 140 MeV/u. The dashed lines indicate the general trends of the distributions
To analyze the characteristics of the fragments produced by different projectiles in projectile fragmentation reactions,the production cross sections as functions of Z and A for the fragments in the48Ni+9Be (a),49Ni+9Be (b), and50Ni+9Be (c) reactions at 140 MeV/u are presented in Fig. 4. As the mass number of the projectile increases, the mass of the fragments produced slightly increases.Additionally, there was a plateau near Z =16 in all three reaction systems, where most of the fragments in this region were produced from the projectiles. The dashed lines indicate the general trends in the three distributions.The slopes of the dashed lines are 1.54, 1.62, and 1.69,corresponding to the reactions48Ni+9Be,49Ni+9Be, and50Ni+9Be, respectively. An increase in the slope indicates that proton-rich fragments are difficult to produce in the reaction induced by the50Ni projectile,which is consistent with Fig. 2.
The48Ni+9Be reaction at 345 MeV/u provides a significant advantage for producing new proton-rich nuclei with Z =20-25 as discussed above. To observe the relationship between the calculated nuclei near the proton drip line and experimentally synthesized nuclei with higher intuition, a nuclear chart of the predicted fragments with Z =20-25 for the48Ni+9Be reaction at 345 MeV/u is shown in Fig. 5.The filled and open squares denote known and unknown nuclei, respectively. Black, red, and brown are stable, β+decay, and p decay, respectively. The production cross sections of unknown nuclei in the48Ni+9Be reaction at 345 MeV/u are indicated by open squares in the figure. From the figure, it can be observed that the produced new nuclei are mainly distributed in the vicinity of the projectile (Z = 28) because the new nuclei are almost formed by the projectile sources in the region of highly peripheral collisions[30].In the projectile fragmentation of48Ni+9Be, 13 new proton-rich nuclei with Z =20-25 have been predicted as follows:34Ca(0.14 mb),37Sc(18.2 mb),38Sc (60.3 mb),38Ti (2.61 mb),40V (12.8 mb),41V(46.5 mb),42V (17.2 mb),40Cr (15.7 μb),41Cr (1.70 mb),42Mn (75.4 μb),43Mn (9.53 mb),44Mn (21.1 mb), and45Mn (2.08 mb). Additionally, an empirical approach was applied to determine the binding energies and to predict the cross sections for isotopes with Z =22-28 near the proton drip line(see Refs. [100,101]).It is evident that the selection of the optimal reaction system should consider not only the production cross sections of fragments but also various factors such as experimental feasibility and detection efficiency. In any case, with the improvement of the experimental condition technology, it is expected that the generation of new proton-rich nuclei with Z =20-25 via the48,49,50Ni+9Be reaction is imminent.

Fig. 5 (Color online)The neutron-deficient nuclei with Z =20-25 on the nuclear map. The filled and open squares denote known and unknown nuclei, respectively. Black, red, and brown are stable, β+decay, and p decay, respectively. The production cross sections of unknown nuclei in the 48Ni+9Be reaction at 345 MeV/u are indicated by the open squares in the figure
4 Summary
In conclusion, fragmentation isotopic distributions were calculated for58Ni on9Be target using the IBLE model for hard and soft symmetry energies.The IBLE model for soft symmetry energy leads to a good description of the crosssection distributions, and the measured cross sections of fragments are reasonably reproduced by the IBLE model,which indicates that the IBLE model can be applied to predict the production cross sections of proton-rich fragments in projectile fragmentation. When considering isospin effects, the48Ni-induced reaction produces more new nuclei and has the largest production cross sections when compared to the49Ni and50Ni projectiles because it has the largest absolute value of isospin and can produce fragments with the greatest proton abundance. Therefore, the48Ni+9Be reaction is promising for producing proton-rich nuclei with Z =20-25. The production cross sections of the new nuclei become larger as the incident energy increases, but this effect becomes weak when the incident energy is higher than 200 MeV/u. The results show that when compared to 140 and 240 MeV/u,the predicted cross sections of new proton-rich nuclei with Z =20-25 are the highest at 345 MeV/u.The isospin of the projectile and incident energy play important roles in projectile fragmentations. In the reaction of48Ni+9Be at 345 MeV/u, 13 new nuclei near the proton drip line were produced in simulations in the vicinity of the projectile (Z =28). The predicted production cross sections of the new nuclei34Ca,37,38Sc,38Ti,40,41,42V,40,41Cr, and42,43,44,45Mn range from 10-2to 102mb. Hence, the generation of new proton-rich nuclei with Z =20-25 via projectile fragmentations using secondary radioactive ion beams of48,49,50Ni is promising for future studies.
 Nuclear Science and Techniques2022年5期
Nuclear Science and Techniques2022年5期
- Nuclear Science and Techniques的其它文章
- Spatial resolution and image processing for pinhole camera-based X-ray fluorescence imaging: a simulation study
- Picosecond time-resolved X-ray ferromagnetic resonance measurements at Shanghai synchrotron radiation facility
- Nonrecursive residual Monte Carlo method for SN transport discretization error estimation
- Density fluctuations in intermediate-energy heavy-ion collisions
- Isospin effects on intermediate mass fragments at intermediate energy-heavy ion collisions
- Identification of anomalous fast bulk events in a p-type pointcontact germanium detector
