Density fluctuations in intermediate-energy heavy-ion collisions

Cong Liu · Xian-Gai Deng· Yu-Gang Ma

Abstract Within the framework of the isospin-dependent quantum molecular dynamics model, we simulate 129Xe+119Sn collisions in an incident energy range of 20 to 190 MeV/nucleon and discuss the liquid-gas phase transition with density fluctuations. For comparison, we also extract the effective Fisher parameter τeff, multiplicity of intermediate-mass fragments (IMFs), and information entropy.It is found that the Fisher parameter and maximum information entropy of collisions have peak values at Ebeam ＝50–80 MeV/nucleon. In addition, the maximum multiplicity of IMFs has a plateau around 70 MeV/nucleon.For higher-order density moments in a larger central region of [-5，5]3 fm3 in the collision system, a maximum plateau also appears as function of beam energy at energies exceeding 70 MeV/nucleon. These observables, which are consistent with each other, indicate a liquid-gas phase transition around 70 MeV/nucleon for the 129Xe+ 119Sn system.

Keywords Heavy-ion collisions · Liquid-gas phase

1 Introduction

Exploration of the phase change and equation of state(EOS) of nuclear matter during heavy-ion collisions is an important topic in nuclear physics [1–6]. It is also closely related to the nuclear transport properties [7–15], nuclear landscape, and nuclear synthesis [16–23]. In the late twentieth century,the relationship between the temperature and excitation energy of the system was found to exhibit behavior similar to the macroscopic phenomenon of the liquid-gas phase transition(LGPT)of classical fluid,and it was proposed that a first-order LGPT, and even a secondorder phase transition at the critical point,occur in nuclear matter [24]. One expects that in a finite-size system of heavy-ion collisions, the LGPT could appear. The LGPT has been investigated in intermediate-energy heavy-ion collisions, both theoretically and experimentally [25–34].In recent decades, many probes have been proposed for determining whether the LGPT has occurred, for example,the caloric curve [25–28], intermediate-mass fragments(IMFs) [35, 36], Fisher’s power-law exponent of the fragment distribution[35–39],the charge fluctuation of the largest fragment [27, 40–42], the negative heat capacity[43],the information entropy[44–46],and the nuclear Zipf law of Ma [44, 47, 48].

Furthermore, recent research has focused on density fluctuations with the goal of investigating the phase transition theoretically and experimentally as in Refs. [49–51].The normalized (net) baryon density moments, which are related to the relative production yield of composite baryons, are observationally relevant and may be useful for exploring phase transitions by enhanced production of composite particles [49–53]. The density moment is expected to be an alternative way of identifying the phase transition in heavy-ion collisions.

Because density fluctuations could be associated with the LGPT, the density moments are calculated to investigate the energy dependence and identify the transition. In this study, we explore the dependence of the density moments on the incident energy in intermediate-energy heavy-ion collisions. Within the framework of the isospindependent quantum molecular dynamics (IQMD) model,central129Xe+119Sn nuclear collisions are simulated, and the density moments are calculated. For verification, the power-law fits of the charge distribution of fragments,fragment multiplicities, and information entropy are presented.

This paper is organized as follows.In Sect. 2,the IQMD model is introduced briefly, and some formulas are presented. In Sect. 3, different LGPT probes are calculated,the maximum values of the density moments are extracted,and the results are discussed. In Sect. 4, a conclusion is presented.

2 Model and formalism

2.1 IQMD model

The QMD model is essentially a quantum extension of the classical molecular dynamics approach, which is widely applied in chemistry and astrophysics;it is designed to describe fragment formation [54–58]. This n-body approach uses a microscopic framework that treats the dynamics of colliding nuclei directly and simulates heavyion collisions on an event-by-event basis [54]. The descriptions of mean positions and momenta are purely classical,and particles are considered to be distinguishable in the QMD model[55].In this work, we use an improved version of the QMD model that incorporates isospin-dependent interactions and the Pauli exclusion principle. In this model, each nucleon is treated as a Gaussian wave packet in a coherent state [54, 55, 59]:

In this work, we set α ＝-129 MeV, β ＝59 MeV, and γ ＝2.09, which is called the hard EOS, and α ＝-390 MeV, β ＝320 MeV, and γ ＝1.14, which is called the soft EOS.

2.2 Formulas

The following probes are calculated on the basis of information on the phase space and fragments: the Fisher parameter τeff, fragment multiplicity, information entropy(H), and density moments. The effective Fisher parameter τeffcan be obtained from the charge distribution by powerlaw fitting as follows:

Fig. 1 (Color online) Charge distributions of the systems in freezeout stage(t ＝300 fm/c)at beam energies of E of a 20 MeV/nucleon,b 50 MeV/nucleon,c 80 MeV/nucleon,and d 130 MeV/nucleon.The red lines represent the Fisher power-law fits in the charge range 3 ≤Z ≤7 for the hard EOS

3 Calculations and discussion

Simulations were performed using the IQMD model for central collisions of129Xe+119Sn at various beam energies ranging from 20 to 190 MeV/nucleon. Both the hard and soft EOSs were considered. The calculated time range was 0–800 fm/c. The density moments were calculated within central regions consisting of [-3，3]3and[-5，5]3fm3cubic boxes, whose centers are located at the center of mass of the collision system,to check the central area dependence of the observables.

3.1 Time evolution of properties

Figure 2 shows the time evolution of the IMF multiplicity （NIMF） and information entropy (H) at various incident energies. In Fig. 2a, the IMF multiplicity increases, reaches a maximum, and then decreases with increasing time. Here, IMFs are defined as fragments with charge number (Z) greater than or equal to 3 and smaller than the charge number of the source. As the energy increases, the IMF multiplicity changes more rapidly.Thus,at higher energies,the collision system generally has a higher excitation energy and breaks more rapidly into numerous fragments.

Using the distribution ｛fi｝ calculated from all events,one can obtain the information entropy (H), as shown in Fig. 2b. The pattern of H evolution is slightly different from that of the IMF multiplicity. With increasing H, the system becomes more chaotic. In the compression stage,the information entropy increases rapidly. With increasing time, more fragments are created, and the multiplicity probability distribution fibecomes more diverse. As time increases further, the information entropy decreases slightly because long-term binding of nucleons in clusters is difficult under the IQMD Hamiltonian.Thus,the number of particles produced will increase with time, which will result in a change in the probability distribution fiand finally a slight decrease in H.

Fig. 2 (Color online) Time evolution of a IMF multiplicity and b information entropy at different beam energies for the hard EOS

Fig. 3 (Color online) Time evolution of a normalized density moments for the orders N ＝2 and b N ＝6 at different beam energies.Here,the normalized density moments are calculated for the central region of [-3，3]3 fm3 for the hard EOS

Fig. 4 Extracted values of a effective Fisher parameter (τ), b maximum values of IMF multiplicities(),and c maximum values of information entropy(Hmax)as a function of incident energy for the hard and soft EOSs

Figure 3 shows the time evolution of the normalized density moments (〈ρN〉/〈ρ〉N), which is the major focus of this work, in the central region of [-3，3]3fm3at various incident energies for N ＝2 and 6. The time evolution of the normalized density moments is similar to that of the IMF multiplicity. It increases with time and then shows near-saturation or a slight decrease. At a given energy, for higher-order density moments, the density moment values are larger. In particular, high-order moments show cleaner structure as a function of beam energy, that is, a clearer broad peak structure at a certain energy,although there are larger fluctuations, as shown in Fig. 3b, because obtaining higher-order density moments with the same precision requires better statistics. In addition, higher-order density moments are more sensitive to density fluctuations.

3.2 Discussion of liquid-gas phase transition

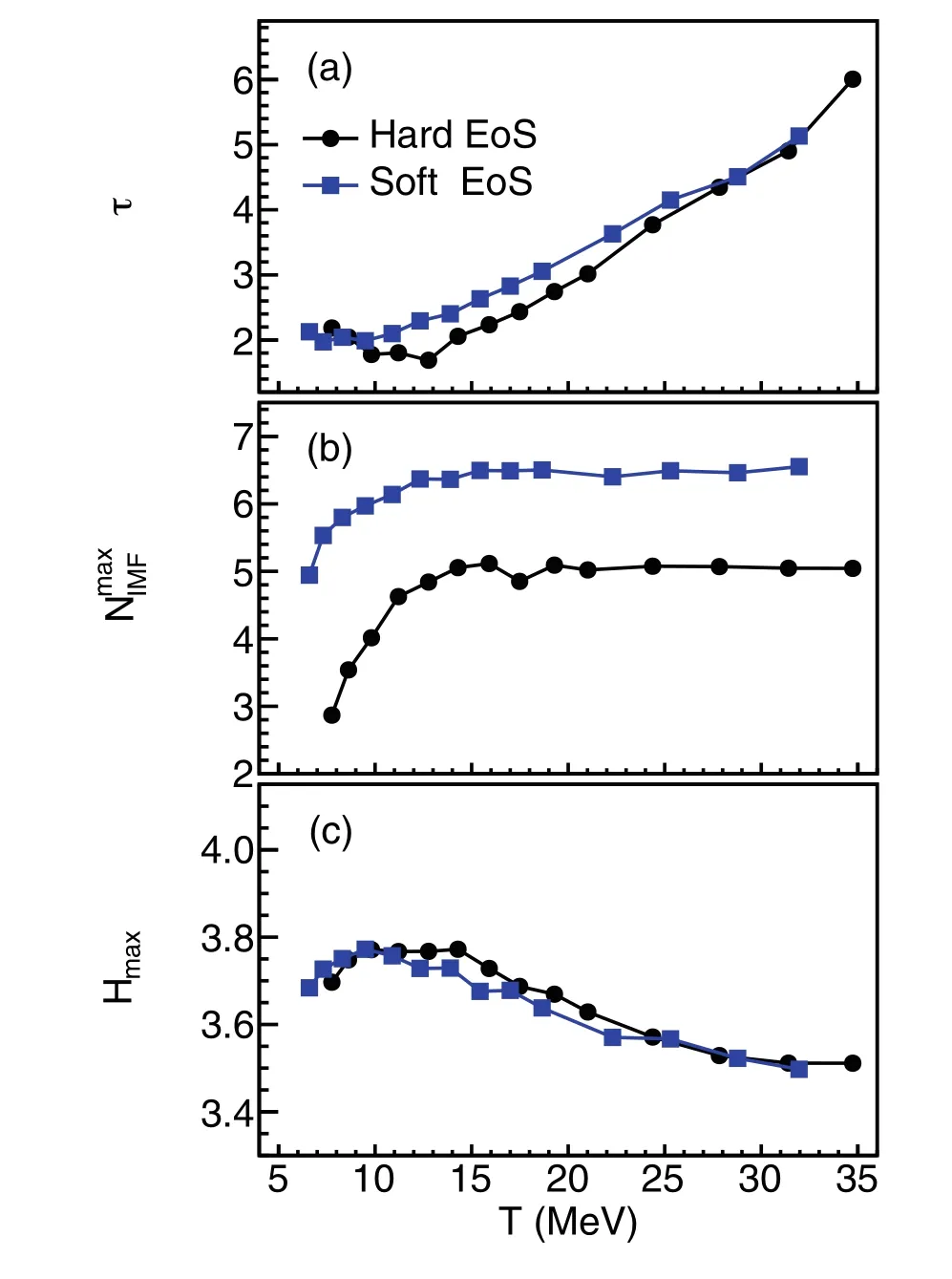
Fig. 5 Same as Fig. 4 but as a function of temperature

Further, we give the maximum normalized density moments for different orders, as shown in Fig. 6. To present all the orders of the normalized density moment in a single figure, these lines are scaled by different factors. In addition, because statistical fluctuations exist, these lines are fitted by polynomial functions. For the order N ＝2(black dotted line in Fig. 6a), the line seems flat. As the order of the density moment increases to N ＝6, the maximum values appear around E ＝90 MeV/nucleon, as shown in Fig. 6b. Thus, the collision system has the maximum density fluctuation around E ＝90 MeV/nucleon,indicating that the LGPT could occur here when the system enters spinodal instability[53, 61].However, if we choose a larger central region of [-5，5]3fm3, as shown in Fig. 7, the maximum normalized density moments reach maximum values around 70 MeV/nucleon and have a plateau at higher incident energies,like the maximum IMF multiplicity shown in Fig. 4b. This energy is also close to the energy given by the effective Fisher parameter τ and the maximum information entropy,as shown in Fig.4a and 4c.

Note that the turning energy varies with the central region. That is, the turning point has regional dependence.In fact,this can be understood from the central densities of the selected regions.We found that the[-3，3]3fm3region can reach a higher average density than the [-5，5]3fm3region.Thermodynamically,the temperature,pressure,and density are correlated; therefore, the turning point of the energy depends on the density.Actually,as reported in our previous work[62],the temperature extracted from heavyion collisions is lower for a smaller central region,where a higher beam energy would be required to reach the same temperature in a smaller central region. Thus, the calculated density moments for a region of a certain size correspond to a certain density and temperature. The[-5，5]3fm3is generally a more reasonable option,because our other observables, that is, the fragment distributions and their effective Fisher parameters, the IMF multiplicities, and the information entropy, are those of the entire space.

Fig. 6 (Color online) Maximum values of normalized density moments for N = 2, 3, 4, 5, and 6 as a function of incident energy in central region of[-3,3]3 fm3.The lines are the fitted results for the hard EOS

Fig. 7 (Color online) Same as Fig. 6, but for central region of[-5，5]3 fm3

4 Conclusion

Heavy-ion collisions of129Xe+119Sn were simulated by the IQMD model. We calculated the fragment charge distribution, IMF multiplicity, and information entropy.Turning points were found at E ＝50–80 MeV/nucleon from the effective Fisher parameter τeffof the fragment charge distribution, maximum IMF multiplicity, and maximum information entropy as a function of incident energy,which are associated with the LGPT. In addition, the turning energy extracted using τeffseems to be smaller than that obtained using the IMFs. For both the hard and soft EOSs, the turning beam energies from all of the above observables of the phase change are not sensitive to the EOS, but a soft EOS could reduce the phase transition temperature of this collision system. Furthermore, we analyzed the density fluctuations in heavy-ion collisions with density moments of different orders. The obtained turning points are close to those given by effective Fisher parameter, IMF multiplicity, and information entropy. For higher-order normalized density moments, there are also peaks or saturation regions versus beam energy, which have the same properties as those obtained using the IMF multiplicity and information entropy. However, they depend on the size of the region;that is,they are pressureor density-dependent.