Isospin effects on intermediate mass fragments at intermediate energy-heavy ion collisions
Li Li · Fang-Yuan Wang · Ying-Xun Zhang,2
Abstract In this study, we investigated the isospin properties of intermediate mass fragments (IMFs) for the central collisions of 112,124Sn+112,124Sn at a beam energy of 50 MeV per nucleon using an improved quantum molecular dynamics model (ImQMD) coupled with a sequential decay model(GEMINI).Three observables were analyzed:(1) the average center-of-mass kinetic energy per nucleon〈Ec.m./A〉 of fragments as a function of their charge number Z; (2) the average neutron number to proton number ratio (〈N〉/Z) of fragments with a given charge number Z as a function of their center-of-mass kinetic energy per nucleon (Ec.m./A); and (3) the average total neutron number to total proton number ratio (∑N/∑Z)and double ratio (DR(N/Z)) of IMFs with Z = 3–8 as a function of their center-of-mass kinetic energy per nucleon Ec.m./A. Our calculations revealed that the sensitivity of the isospin properties of IMFs relative to the stiffness of the symmetry energy remains even after sequential decay. By comparing the calculations of ∑N/∑Z and DR(N/Z)with the data, it was found that the soft symmetry energy,i.e., γ =0.5, is favored.
Keywords Symmetry energy · Intermediate mass fragments · Isospin effects
1 Introduction



However, there is tension around the symmetry energy constraints following the Lead Radius Experiment(PREXII) reporting of a model-independent extraction of the neutron skin of208Pb and Δrnp =0.283±0.071 fm [36].Yue et al. [17]analyzed newly published neutron skin data with ground-state properties and giant monopole resonances of finite nuclei, the properties of neutron stars for PSR J0740+6620,the mass-radius of PSR J0030+045,and the neutron star tidal deformability extracted from the GW170817 event to obtain the constraints of symmetry energy in a large density region. Their calculations suggested that S(ρ0)=34.5±1.5 MeV and L =85.5±22.2 MeV. The values obtained are consistent with the constraints of the symmetry energy from the SπRIT data [13]for Sn+Sn at 270A MeV, but are less than the values obtained for the analysis of PREX-II using a specific class of relativistic energy density functional [36],in which L =106±37 MeV and S0=38.7±4.7 MeV. Their constraints on the symmetry energy also overlap with the symmetry energy extracted from the charge radius of54Ni,where 21 MeV <L<88 MeV [37], and the combination of astrophysical data with PREX-II and chiral effective field theory, where L =MeV [38].Currently, the big challenge in constraining the density dependence of the symmetry energy with HICs is to understand the model dependence and reduce the uncertainties of the symmetry energy constraints. The understanding of the model dependence has been achieved in the last 10 years via the transport model evaluation project,and significant progress has been made in the treatment of nucleon-nucleon collisions and the mean-field potential [39–43]. The reduction in the uncertainties of symmetry energy constraints is still underway, which can be realized by simultaneously describing multi-observables using transport models. The data for isospin-sensitive observables from intermediate-energy HICs, such as isoscaling [44],double neutron to proton ratio [45],isospin diffusion [46], rapidity dependence of the isobaric ratio [10], and neutron-excess to proton ratio [11], have been used for comparison with the predictions from different transport models [4, 5]. Among these transport models, the ImQMD model successfully describes the neutron-to-proton yield ratio (n/p ratio), isospin diffusion,and isospin transport ratio as a function of rapidity, and constraints on the symmetry energy at the subsaturation density have been achieved [5].
Except for the aforementioned isospin-sensitive observables, the neutron number divided by the proton number of IMFs was considered to be complementary information of the neutron-to-proton yield ratio and can be used to extract information related to the symmetry energy [6]. This can be explained by the multi-fragmentation mechanism where the copious production of IMFs and its isospin contents are closely related to the dynamic mechanism of the HICs [47–49].
The measurement of IMFs has been performed at the National Superconducting Conducting Cyclotron Laboratory at Michigan State University [50], but there are few models for the theoretical analysis of the isospin effects of IMFs and their use to constrain the symmetry energy.Thus,it is worth to check whether the ImQMD model can simultaneously describe the isospin properties of IMFs.
In this study, we focus on the properties of IMFs(Z =3-8) for the central collision (b =2 fm) of112,124Sn+112,124Sn at Ebeam=50 MeV/u using the ImQMD model coupled with the GEMINI model. Furthermore, we compared the calculated results to the data for learning the form of the symmetry energy and the reaction dynamics.
2 Theoretical model and symmetry energy
The version of ImQMD used in this study was the same as that used in Ref. [5], i.e., ImQMD05, in which the isospin-independent momentum-dependent interaction was utilized. To simulate low-intermediate energy HICs, the basic properties of the initial nuclei are important,and they are guaranteed by requiring that the binding energy and root-mean-square (rms) radius of the sampled nuclei fall within the range of the experimental data with specific uncertainties. For the standard initialization treatment, the initial nuclei remain stable within 200 fm/c, which is sufficient for Sn+Sn at 50 MeV/u because the reaction dynamics are completed within 100 fm/c [51]. Additional details regarding the initialization of the ImQMD model can be found in Refs. [51–55].
The nucleonic mean field potential is derived from the Skyrme-type energy density functional, and the energy density of the symmetry potential is as follows:

The ImQMD simulations were terminated at 400 fm/c when the systems reached ‘‘dynamical freeze-out.’’ The primary fragments were recognized using the isospin-dependent minimum spanning tree method [51], and the excitation energy was calculated in the rest frame of the fragment by subtracting the ground state energy from the energy of the fragment in its rest frame.It should be noted that the fragments produced during the ImQMD calculations are primary, and they may have very neutron-rich or very neutron-poor‘‘unphysical’’fragments.The probability of generation of these ‘‘unphysical’’ primary fragments is tiny in ImQMD simulations,and their ground state energies are approximately obtained using the liquid-drop mass formula.
The sequential decay of the primary fragments was performed using the GEMINI code [56, 57], which describes the de-excitation process of the compound nucleus and facilitates binary decay, including light-particle evaporation and symmetric fission. The decay continues until the particle emission is energetically forbidden or impossible owing to competition with γ-ray emission.

Table 1 The symmetry energy coefficient and slope of the symmetry energy correspond to the parameters used in ImQMD05. S0, L and S(2ρ0) are in MeV, γ is dimensionless
3 Results and discussions
Before studying the isospin properties of the IMFs, we focused on the cluster formation mechanism of HICs.Figure 1 shows the time evolution of the multiplicities of emitted nucleons (top panels) and fragments (bottom panels), for the collisions of124Sn+124Sn and112Sn+112Sn.It is evident that the nucleons are emitted prior to IMFs with Z =3-8, and IMFs with Z =3-8 prior to fragments with Z =9-20. For example, for the reaction system112Sn+112Sn,the emission of nucleons begins from t ~50 fm/c, but the emission of IMFs with Z =3-8 occurs at approximately t ~100 fm/c and Z =9-20 fragments at approximately t ~140 fm/c. Such a dynamic process results in a decrease in the fragment velocity with the fragment charge number. After t ~250 fm/c, the primary fragments are completely formed.Ideally,the system should be in ‘‘dynamical freeze-out,’’ and its multiplicities should not change with time.However,it is difficult for the QMD type Hamiltonian to bind the fragments for a long time, and the pseudo-emission of nucleons occurs at the late stage of the simulations of HICs. Therefore, the multiplicities of fragments with Z =3-8 or 9-20 decrease slightly, and the magnitude depends on the stiffness of the symmetry energy.
To understand the influence of different symmetry potentials on the reaction dynamics, we investigated the time evolution of the multiplicities of nucleons and fragments for γ =0.5 (solid lines) and γ =2.0(dashed lines).The results show that the multiplicities of the nucleons and the fragments depend on γ and the isospin asymmetry of the reaction system.
The multiplicities of emitted neutrons calculated with γ =0.5 are greater than those with γ =2.0, and the effect is the opposite for the multiplicities of protons. Consequently,it is expected that the neutron-to-proton yield ratio would be sensitive to the stiffness of the symmetry energy.Numerous studies have investigated for constraining the symmetry energy using n/p ratios [10, 39, 45, 54, 58, 59].
For the multiplicities of fragments with Z =3-8(or 9-20), the calculations show that the multiplicities of IMFs obtained with γ =0.5 are smaller than those with γ =2.0.This is because a higher density is reached in the overlap region and more compressional energy is stored for the soft isospin asymmetric nuclear equation of the state (γ =0.5)compared to that of the stiff isospin asymmetric nuclearequation of state (γ =2.0) in the simulations. Thus, the reaction system simulated with γ =0.5 disintegrates into more light-charged fragments compared to the case of γ =2.0. Owing to the conservation of the nucleon number in the reaction system,the multiplicities for fragments with Z =3-8 (or 9-20) for the γ =0.5 case are smaller than those for γ =2.0.

Fig. 1 (Color online) The time evolution of the multiplicities of nucleons and fragments withZ =3-8 and Z =9-20 for 124Sn+124 Sn (panels a and c)and 112Sn+112 Sn(panels b and d) for different symmetry energy cases



Fig. 2 (Color online) The average kinetic energy per nucleon as a function of the fragment charge number Z. The solid symbols represent γ =0.5 and the open circles represent γ =2.0. The red lines are the results for primary fragments,and the blue lines with symbols represent the cold fragments

where Y(Ni,Z) is the yield of the fragment with a neutron number Niand charge number Z. The summation is for all isotopes at a given Z. As an example, Fig. 3 presents the〈N〉/Z ratio of primary fragments (red lines) as a function of Ec.m./A for fragments with Z =3,4,5,6,7,8. The left six panels are for124Sn+124Sn and the right six panels are for the reaction system112Sn+112Sn.In general,the slopes of the 〈N〉/Z ratio as a function of Ec.m./A are negative,because the Coulomb energy accelerates the neutron-poor fragments to a higher kinetic energy region.These behavior occurs for all elements of the IMFs. Furthermore, the curves of the 〈N〉/Z ratios as a function of kinetic energy Ec.m./A depend on the stiffness of the symmetry energy,and the results obtained for γ =0.5 and 2.0 crossover at a specific energy,Ecross.The values of Ecross increase from 4 MeV to approximately 10 MeV as Z increases from 3 to 8, owing to the Coulomb interaction.


The Coulomb interaction increases the isospin asymmetry of the primary fragments and the symmetry energy term decreases the isospin asymmetry of the fragments. Since the fragments are formed during the expansion phase during which the system is at a subsaturation density, the values of the symmetry energy avsym(ρ,T) obtained for γ=0.5 are larger than those obtained for γ=2.0, and it is expected that the 〈N〉/Z values of the fragments obtained for γ=2.0 will be larger than those for γ=0.5, according to Eq. (6).

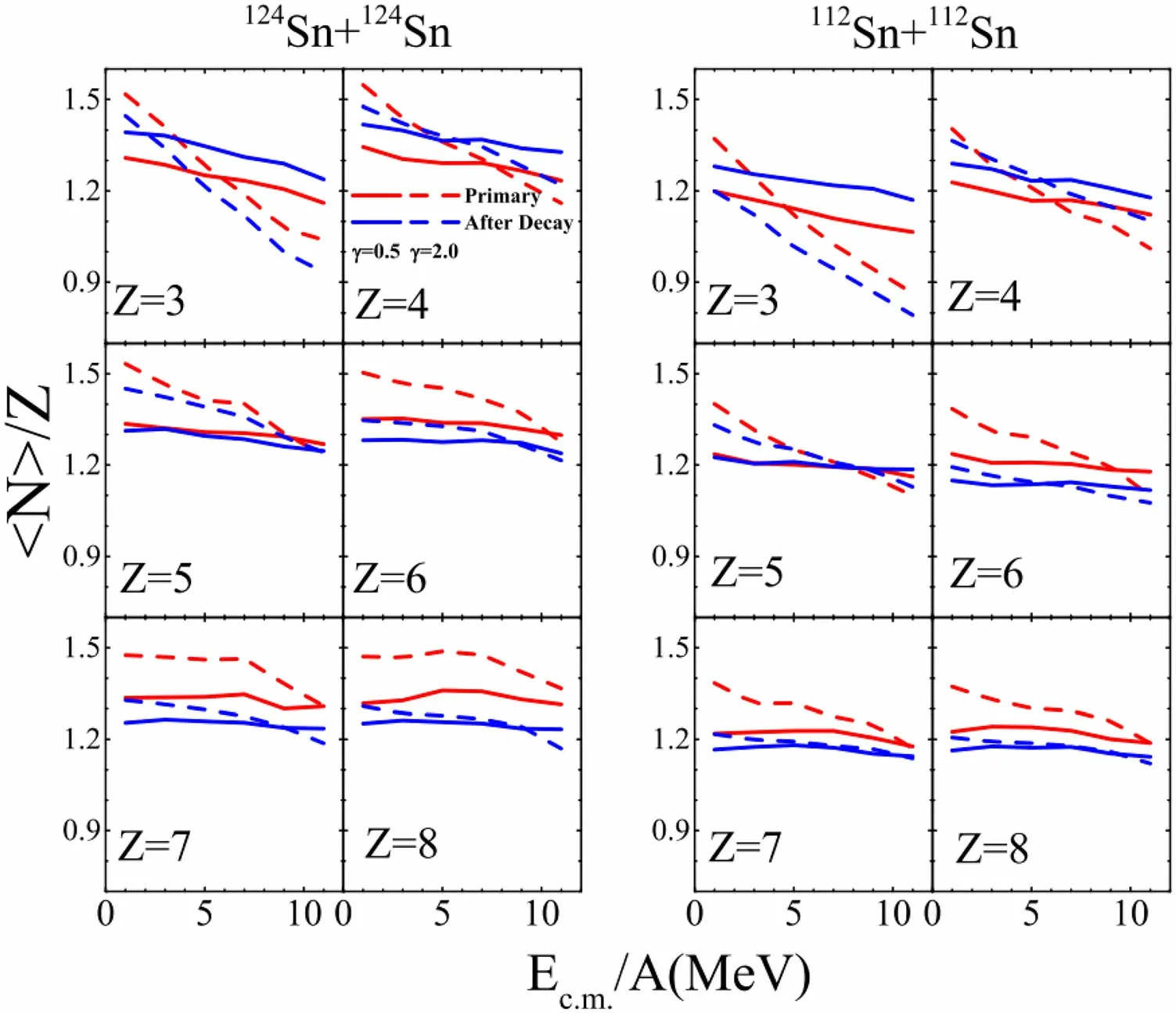
Fig. 3 The 〈N/Z〉ratios as functions of kinetic energy per nucleon for Z = 3, 4, 5, 6, 7, 8 for primary (red lines) and cold fragments (blue lines) obtained for γ =0.5 and 2.0. The left six panels are for 124Sn+124 Sn,and the right panels are for 112Sn+112 Sn




Fig.4 ∑N/∑Z as a function of the kinetic energy per nucleon for 124Sn+124Sn (left four panels) and for 112Sn+112Sn (right four panels).Panel a, b, e and f represent the results for the primary fragments, and c,d,g and h are the results for the cold fragments


The idea of this double ratio is similar to the double neutron-to-proton ratio, which has been used to isolate the isospin effects and constrain the density dependence of the symmetry energy [6, 45, 54]. To obtain good statistics of the results of DR(N/Z) in the transverse direction, we performed simulations with 100,000 events. In Fig. 5a, we present the DR(N/Z) ratios for the cold fragments in the transverse direction for an experimental case such that 70°≤θc.m.≤110°.The shaded region with a solid pattern(dashed pattern) is the result obtained for γ=0.5 (γ=2.0).The DR(N/Z) ratios obtained for γ =2.0 are larger than those obtained for the γ =0.5 case. This can be observed from Fig. 3.These trends reflect the fact that the fragments originate from the composite system that survives the preequilibrium emission,as indicated in Ref.[6].Compared to the data,the calculations for the case of γ=0.5 are favored.We also analyzed DR(N/Z)in the non-transverse direction,and the results are shown in panel (b). The calculations show that the sensitivity of DR(N/Z) to the stiffness of the symmetry energy is maintained in the non-transverse direction, and the DR(N/Z) in the non-transverse direction has good statistics because the IMFs are distributed in the forward and backward regions.

Fig. 5 Double N/Z ratios as a function of the kinetic energy per nucleon. The top panels are the results for the transverse direction,and the bottom panels are the results for nontransverse direction
4 Summary and prospective

Nevertheless, the tight constraints on the symmetry energy still need more work.For example,the effects of the momentum-dependent symmetry potential should be well understood because the isospin-dependent momentum-dependent symmetry potential influences the cluster formation and the n/p ratio of the emitted nucleons [66, 67].Thus,the curves of the average kinetic energy of the IMFs as a function of Z are modified. The ∑N/∑Z ratios and DR(N/Z) may also be influenced by the different signs associated with effective mass splitting. These points should be carefully investigated in the future. Our analysis and experimental studies[50]also suggest that a sequential decay model should be developed.
AcknowledgementsY.Zhang is thankful for the helpful discussions with Prof. M. B. Tsang.
Author ContributionsAll authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Li Li, Fang-Yuan Wang and Ying-Xun Zhang.The first draft of the manuscript was written by Ying-Xun Zhang and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
 Nuclear Science and Techniques2022年5期
Nuclear Science and Techniques2022年5期
- Nuclear Science and Techniques的其它文章
- Spatial resolution and image processing for pinhole camera-based X-ray fluorescence imaging: a simulation study
- Picosecond time-resolved X-ray ferromagnetic resonance measurements at Shanghai synchrotron radiation facility
- Nonrecursive residual Monte Carlo method for SN transport discretization error estimation
- Density fluctuations in intermediate-energy heavy-ion collisions
- Identification of anomalous fast bulk events in a p-type pointcontact germanium detector
- Free-radical evolution and decay in cross-linked polytetrafluoroethylene irradiated by gamma-rays
