Enhanced solution to the surface–volume–surface EFIE for arbitrary metal–dielectric composite objects*

Han WANG，Mingjie PANG，Hai LIN

State Key Laboratory of CAD & CG，Zhejiang University，Hangzhou 310027，China

Abstract: The surface–volume–surface electric field integral equation (SVS-EFIE) can lead to complex equations，laborious implementation，and unacceptable computational complexity in the method of moments(MoM).Therefore，a general matrix equation(GME)is proposed for electromagnetic scattering from arbitrary metal–dielectric composite objects，and its enhanced solution is presented in this paper.In previous works，MoM solution formulation of SVSEFIE considering only three-region metal–dielectric composite scatters was presented，and the two-stage process resulted in two integral operators in SVS-EFIE，which is arduous to implement and is incapable of reducing computational complexity.To address these difficulties，GME，which is versatile for homogeneous objects and composite objects consisting of more than three sub-regions，is proposed for the first time.Accelerated solving policies are proposed for GME based on coupling degree concerning the spacing between sub-regions，and the coupling degree standard can be adaptively set to balance the accuracy and efficiency.In this paper，the reformed addition theorem is applied for the strong coupling case，and the iterative method is presented for the weak coupling case.Parallelism can be easily applied in the enhanced solution.Numerical results demonstrate that the proposed method requires only 11.6% memory and 11.8% CPU time on average compared to the previous direct solution.

Key words: Composite object;Integral equation;Method of moments (MoM);Addition theorem;Iterative method

1 Introduction

The electromagnetic(EM)simulation of metal–dielectric composite structures plays an essential role in many areas of electromagnetism such as planar microstrips，radome analysis，remote sensing，and radar applications (Lu and Chew，2000;Lu，2003;Xie and Li，2018).In previous works (Poggio and Miller，1973;Rao et al.，1982;Ergul and Gurel，2009)，one unknown was enough for a metal object，whereas two unknowns were required to reproduce the sought field throughout a dielectric object in the surface integral equation(SIE).

Recently，the surface–volume–surface electric field integral equation (SVS-EFIE) (Menshov and Okhmatovski，2013;Lori et al.，2018) has been proposed for scattering analysis of two-dimensional(2D)and three-dimensional (3D) dielectric bodies.Furthermore，SVS-EFIE has been applied to dielectric objects in multilayered media (Zheng et al.，2018) and metal–dielectric composite objects (Gholami and Okhmatovski，2020).The analytic solution to SVS-EFIE has also been presented for homogeneous dielectric spheres，which validates the rigorous nature of SVS-EFIE (Goni and Okhmatovski，2021).SVS-EFIE requires only a single unknown on the boundary of the dielectric body to determine the sought field with a two-stage process(Lori et al.，2018).In the first stage，the unknown currents on the boundary of the scatterer were used to obtain the total field distribution throughout the volume of the scatterer.The entire field outside the scatterer was obtained in the second stage by the total field distribution throughout the volume using the volume equivalence principle.However，the two-stage process will generate two additional dense matrices in the method of moments (MoM).Considering a metal–dielectric composite object discretized by tetrahedrons，Nvtetrahedrons in its volume andNstriangle pairs on its boundary were observed，whereNv=andα ∈(1，1.5) (Gholami et al.，2019).In solving SVS-EFIE using MoM with the RWG basis function(Rao et al.，1982)and Galerkin method，Nsunknown coefficients must be determined.Apart from the normalNs×Nsdense matrix，the first-stage process leads to an additionalNs×Nvdense matrix，and the second-stage process leads to an additionalNv×Nsdense matrix.The hierarchical(H-)matrix has been introduced for fast analysis of SVS-EFIE(Gholami et al.，2019).The general mathematical framework of theH-matrix provides a highly compact representation of the impedance matrix，which can reduce the time and memory usage for solving SVS-EFIE.However，theH-matrix accelerated method does not consider the difference between the strong coupling and weak coupling cases among the composite objects.Moreover，although SVS-EFIE has been applied to metal–dielectric composite objects in Gholami and Okhmatovski (2020)，only the MoM solution formulation considering three-region metal–dielectric composite scatterers has been presented.Therefore，although SVS-EFIE can effi-ciently reduce the number of unknowns in SIE for dielectric scatterers，solving SVS-EFIE using MoM will result in complex equations，laborious implementation，and unacceptable computational complexity.

To address these problems，an enhanced solution to SVS-EFIE for arbitrary metal–dielectric composite objects is proposed in this study.MoM is the core solver of the enhanced solution.In addition，CPU parallelism(Dagum and Menon，1998;Hariharan et al.，2002)can be easily applied to improve the computational efficiency of the accelerated methods.Two main contributions of this paper are as follows:

1.A general matrix equation (GME) is presented to solve SVS-EFIE for arbitrary metal–dielectric composite objects using MoM.The new GME is highly adaptive to homogeneous objects and composite objects that consist of more than three sub-regions.Furthermore，GME has a simple form that is easy to implement on computers.

2.An enhanced solution to GME is presented.Two acceleration policies are proposed for solving GME based on coupling degree，which can be set adaptively to balance the accuracy and efficiency.For the strong coupling case，the addition theorem，which has been widely used in computational electromagnetics，is adopted to accelerate matrix–vector multiplication (MVM) and matrix–matrix multiplication (Song J et al.，1997;Chew et al.，2001).For the weak coupling case，the iterative method is adopted to consider the weak coupling among different parts，and adaptive cross approximation(ACA)(Zhao et al.，2005) is introduced to compress the coupling matrix among different sub-regions.In the enhanced solution，computational complexity is reduced toO(NαslogNs)，whereNsis the number of total triangle pairs on the boundary of the composite objects.

2 Basic principle of SVS-EFIE

Consider the scattering of the time-harmonic incident fieldEincon a homogeneous dielectric object of volumeV.Using the volume equivalence principle，the electric field inside and outside the scatterer can be defined as

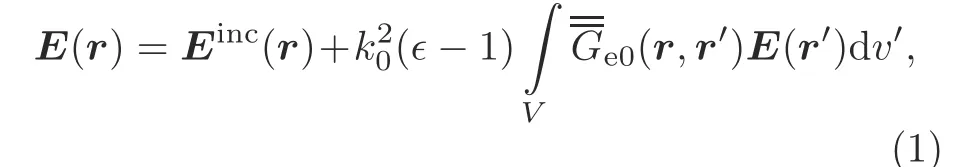
whereris the observation point in the space，r′is the source point inside the scatterer，∈is the complex relative permittivity，is the wavenumber of vacuum，and∈0andμ0are the permittivity and permeability of vacuum，respectively.The 3D dyadic Green function of free space is

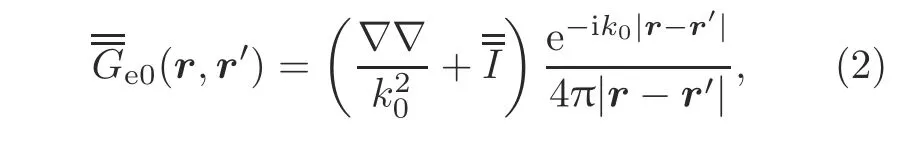
whereis the idem-factor.

By the homogeneous wave equation，the total electric field inside the scattererVsatisfies

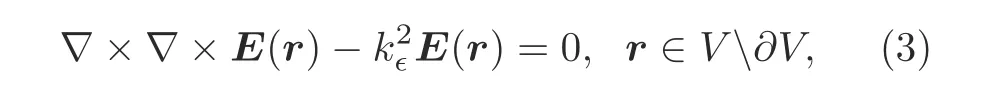
whereis the wavenumber inside the homogeneous non-magnetic medium.

It can be written as a superposition of spherical waves emanating from object boundary∂Vas

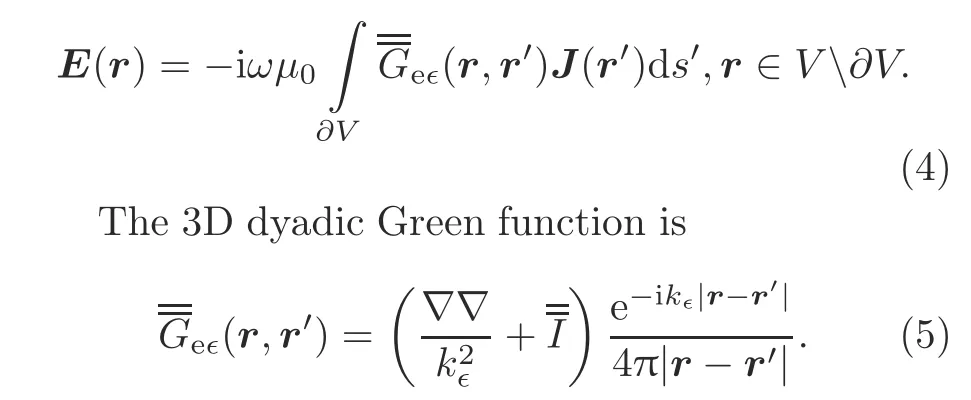
Substituting Eq.(4)into Eq.(1)and restricting the observation domain to the surface of the scatterer yields SVS-EFIE as(Lori et al.，2018)

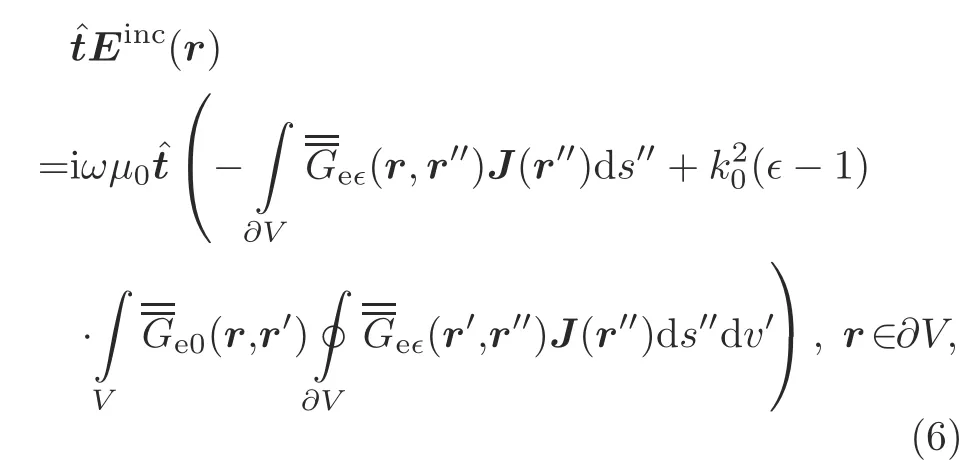
3 GME of SVS-EFIE for composite objects

SVS-EFIE was extended to SVS-surface-EFIE(SVS-S-EFIE) for composite conductor–dielectric materials by Gholami and Okhmatovski(2020)，but only the MoM solution formulation for three-region composite objects was presented.Here，we present a general solution form to SVS-EFIE based on the MoM for arbitrary metal–dielectric composite objects.Homogeneous objects and composite objects consisting of more than three sub-regions can be easily expanded from GME.

Consider an arbitrary metal–dielectric composite object that consists ofPcconductor regions andPddielectric regions.The index range of the metal regions is from 1 toPc，and the index range of dielectric regions is fromPc+1 toPc+Pd.By the equivalence principle and enforcement of the vanishing tangential electric field on the surface of the metal region，the sum of the tangential part of the incident field and the total scattered field generated from all sub-regions of the composite objects on the metal region surface equals zero.By the volume–surface equivalence principle (Lu and Chew，2000;Xie and Li，2018)and restricting the observation point to the boundary of the dielectric region，the tangential part of the total field of the dielectric region’s boundary is equal to the sum of the incident field of the region and scattered field generated from all the sub-regions of the composite objects.Adjusting these pieces of information，the extended SVS-EFIE for composite objects is represented as

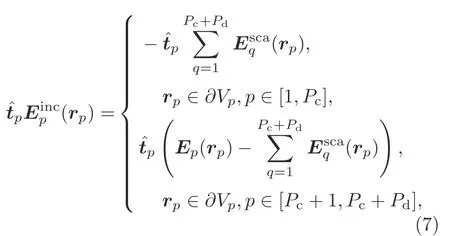
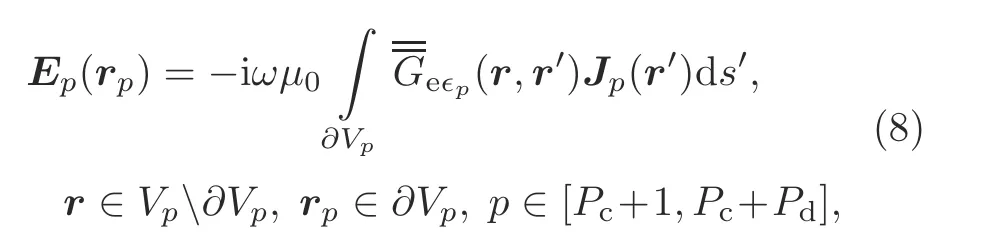
whereJpis the unknown equivalent current on the boundary of regionp.The Green function of the dielectric regionpis

By the surface equivalence principle and Eq.(6)，the scattered field from different sub-regions is represented in Eq.(10) at the top of the next page.In Eq.(10)，Jqis the unknown equivalent current on the boundary of regionq，∂Vqis the boundary of the metal regionq，Vqis the volume of the dielectric partq，and∈qis the complex relative permittivity of the dielectric regionq.

Combining Eqs.(7) and (8)，the general form of the SVS-EFIE for composite conductor–dielectric materials is produced in Eq.(10).In solving equations using MoM，the surfaces of metal regions are discretized by triangles，and the volumes of dielectric regions are discretized by tetrahedrons.The

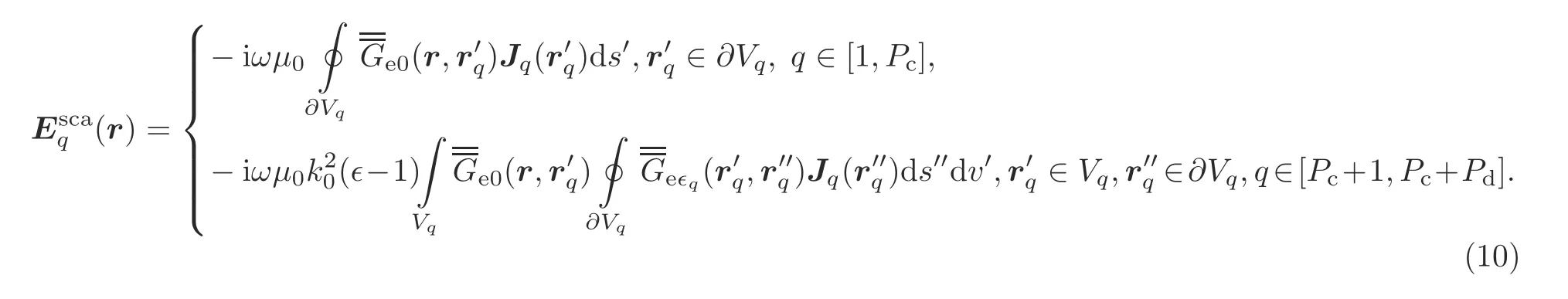
unknown currentsJqdefined on the boundary∂Vqof regionqcan be performed using the RWG basis function (Rao et al.，1982)，which is defined as

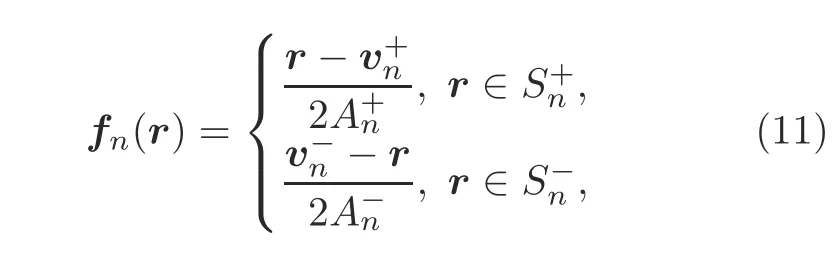
whereis the vertex that is opposite to the interior edge andis the area of triangleas illustrated in Fig.1.

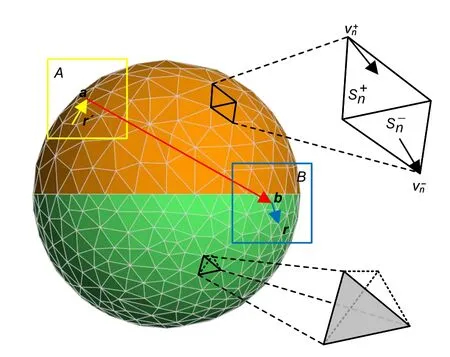
Fig.1 Illustration of the mesh，basis functions，and wave translation

Using the Galerkin method，the GME can be written as

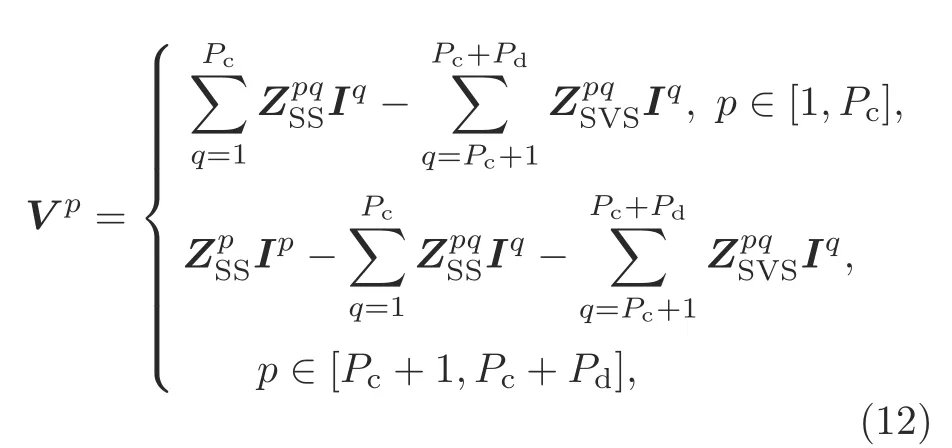
whereV pis the excitation matrix related to the left part in Eq.(7).IpandIqare the unknown surface current coefficients of regionspandq，respectively.The dielectric surface-to-surface integral matrixis generated from Eq.(8)，and the matrix elements are computed by

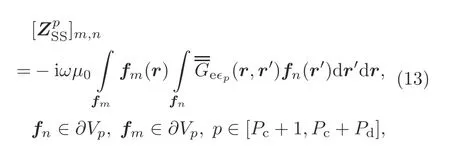
wherefmis the RWG test function andfnis the RWG basis function.

The metal surface-to-surface integral matrixis related to the surface-to-surface integral Eq.(10) from conductor partpto partq，and the matrix elements are calculated by

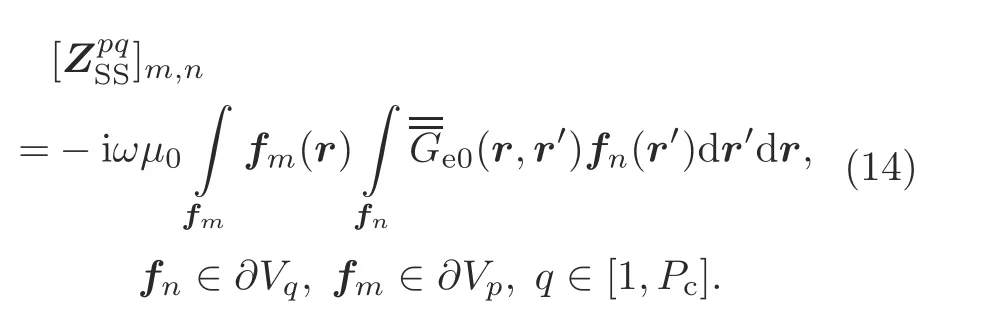
The dielectric SVS integral matrixis related to the SVS integral Eq.(10) from dielectric partpto partq，and the matrix elements are computed by

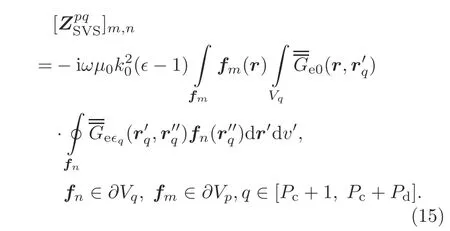
The excitation matrix is calculated by

4 Enhanced solution to GME

The GME of SVS-EFIE can be solved directly，but the computational complexity of the direct solution is unacceptable in practical applications.The dielectric and metal surface-to-surface integral matrices in Eq.(12)requireO()memory storage.In addition，these two dense matrices in Eqs.(17) and(18)requireO(NsNv)memory storage.The SVS integral matrix is generated by the multiplication of two dense matrices，leading to time complexity of.In addition，the direct matrix equation solver for GME requiresO() CPU time.Therefore，given thatNv=andα ∈(1，1.5)，the direct solution to GME hasO(N1+αs)space complexity andtime complexity.

In this study，an enhanced solution of the general form is presented to reduce the computational complexity.Two policies are presented based on the coupling degree concerning the spacing between different sub-regions.For the strong coupling case，the coupling matrices between two sub-regions contribute significantly to the final result.Thus，the coupling matrices should be stored explicitly，and the physical considerations such as the addition theorem are suitable for reducing the computational complexity.For the weak coupling case，the coupling matrices between two sub-regions have a weak influence on the final result.Thus，the coupling matrices can be compressed by an algebraic method such as ACA，and the iterative method is suitable for considering weak coupling.

4.1 Enhanced solution in the strong coupling case

In this study，the method based on the addition theorem is proposed to solve the scattering problems for the composite objects in the strong coupling case.Applying the addition algorithm to the Green function in Eqs.(2)and(9)yields

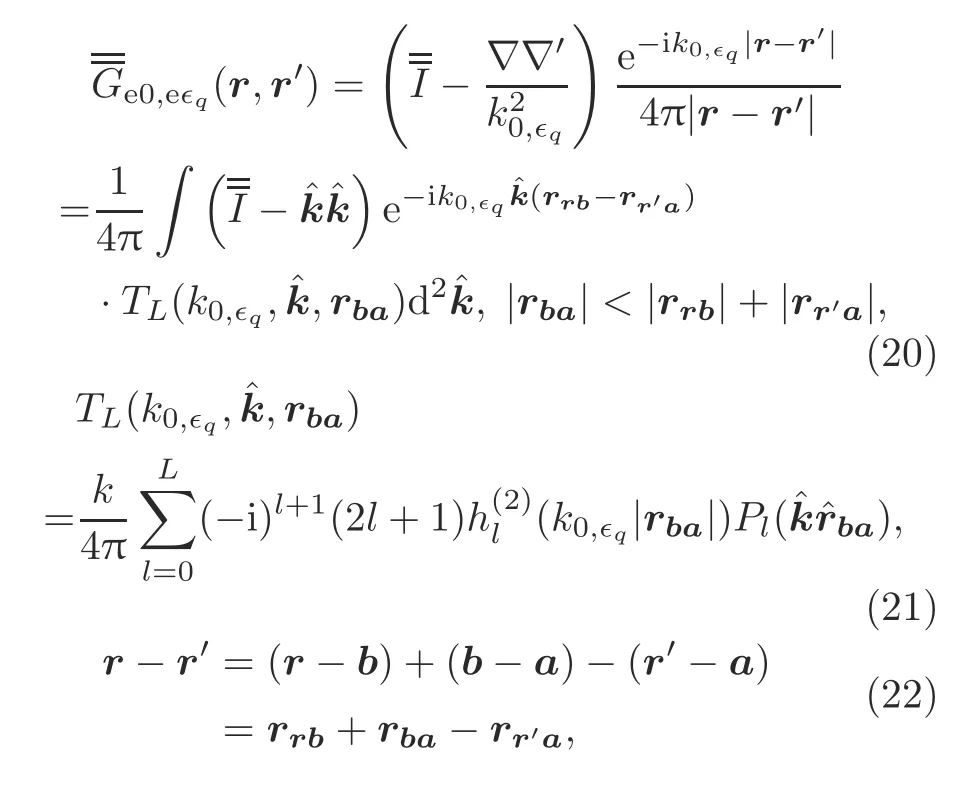
Applying the addition theorem to the four matrix elements shown in Section 3 produces new formulas to calculate the elements that satisfy the constraint in Eq.(20).

1.Applying the addition theorem to Eq.(13)，theelement can be written as

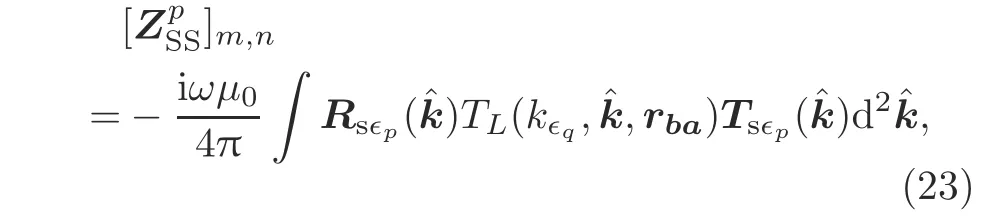
where the radiation function is

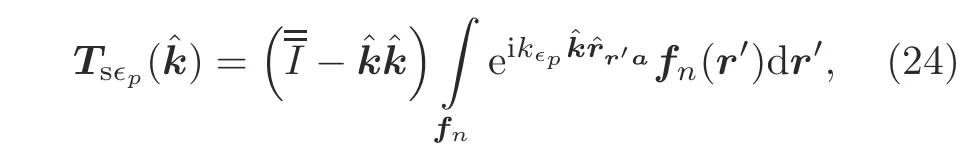
and the receive function is

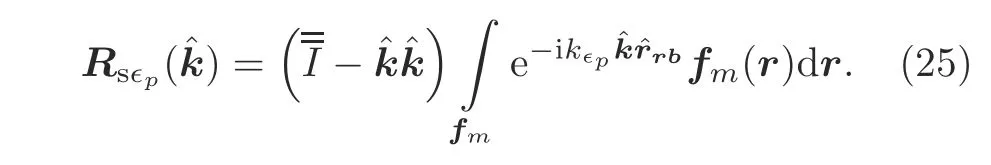
2.Applying the addition theorem to Eq.(14)，theelement can be written as

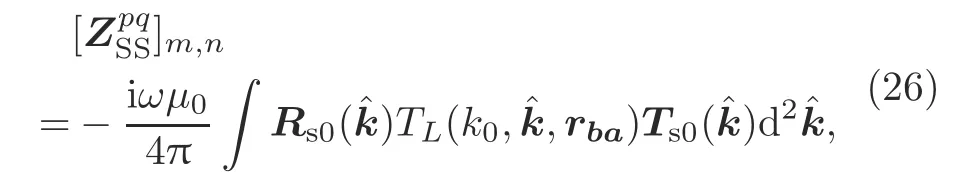
where the radiation function is

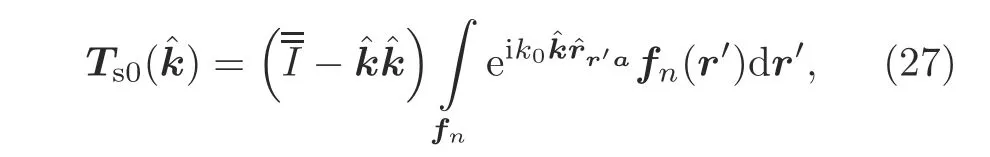
and the receive function is

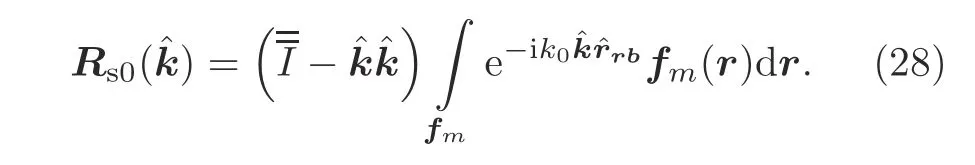
3.Applying the addition theorem to Eq.(17)，theZSVelement can be written as

where the radiation function in the volume-tosurface integral process is

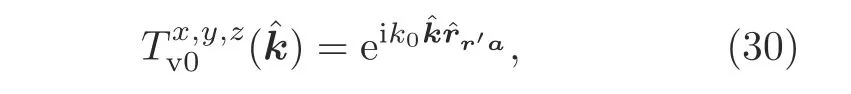
and the receive function defined on the RWG basis functions on the boundary of the scatterer is the same as Eq.(28).

4.Applying the addition theorem to Eq.(18)，theZVSelement can be written as

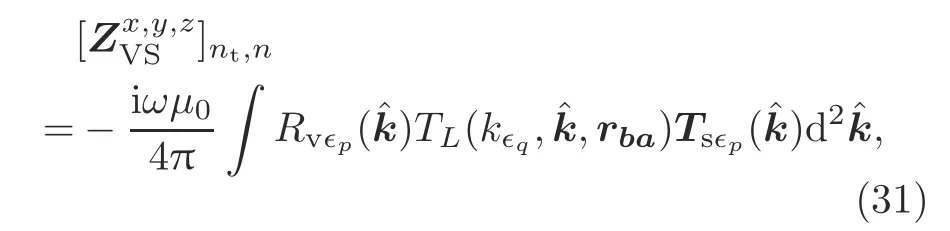
where the element of the radiation function is the same as Eq.(24)，and the receive function in tetrahedron’s volume is

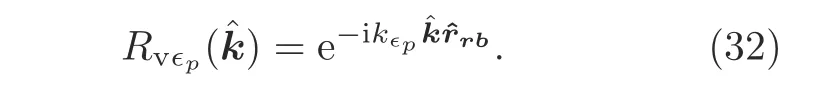
The addition theorem can accelerate MVM in the iterative solver for matrix equations such as the Jacobi method，Gauss–Seidel method，and conjugate gradient method.The MVM based on the addition theorem has three main steps.

First，the tree-based octree subdivision scheme is used to divide the RWG triangle pairs and tetrahedrons into layered cubes (groups) (Meagher，1982).In the octree subdivision scheme，the entire object is enclosed in a large cube，which is then partitioned into eight child cubes.Each child cube is then recursively subdivided into eight smaller cubes as long as the edge length of the finest cube is no less than the threshold (0.25λin this study，whereλis the wavelength).As shown in Fig.1，a cube (group)can contain only RWG triangle pairs from a single region (groupA) or RWG triangle pairs of different sub-regions and tetrahedrons(groupB).

Second，for a cube in each layer，other cubes are marked as the near group，the relatively far group，and the far group based on their positions.If cubeC2adjoins cubeC1，thenC2is marked as a near group ofC1.If cubeC3does not adjoinC1，but their parent cubes are adjoined，thenC3is marked as a relatively far group ofC1.Other cubes in the same layer are marked as far groups ofC1.

Third，the corresponding near-group impedance elements in the finest layer are computed by conventional MoM and stored explicitly.The MVM related to the relatively far group in each layer is accelerated by the addition theorem.Thus，the calculations ofare accelerated through three processes:upward aggregation，translation，and downward disaggregation (Fig.1).For each basis function in the finest layer，the aggregated field to the center of its parent group is calculated by the radiation functions，and its disaggregated field is directly calculated by the receive functions.For each cube，the aggregated field to the center of its parent group is aggregated and interpolated，and the disaggregated field is anterpolated and disaggregated from the center of its parent group (Bucci et al.，1991;Chew et al.，2001;Sarvas，2003).Note that the interpolation and anterpolation are required due to the different sampling rates in different layers when we calculate the integral in Eq.(20).

In the enhanced solution for the strong coupling case，an octree structure withO(logNs) layers will be constructed.In each layer，the aggregation，translation，and disaggregation processes requireO(Nv) memory storage and CPU time (Song JM and Chew，1995).Thus，the enhanced solution in the strong coupling case hascomputational complexity.

4.2 Enhanced solution in the weak coupling case

Considering a composite conductor–dielectric object whose spacing among different homogeneous sub-regions is relatively far(no less than 0.1λin this study)，the coupling among different sub-regions has a weak influence on the final result.Thus，we propose an iterative method to solve GME with weak coupling in this study.The flowchart of the iterative method is illustrated in Fig.2.There are two main processes:the inner solving process and the iteration process.Details of these two processes will be presented in the following subsections.

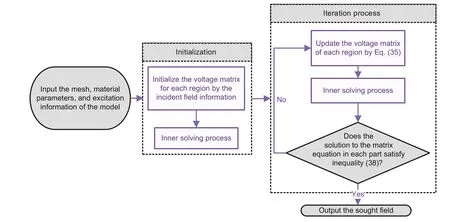
Fig.2 General flowchart of the enhanced solution in the weak coupling case

4.2.1 Inner solving process

In the inner solving process，the octree structure and the addition theorem are used in each homogeneous region as illustrated in Section 4.1.After the incident field is determined，different homogeneous parts are solved independently.In this implementation，the inner solver of the conductor parts solves

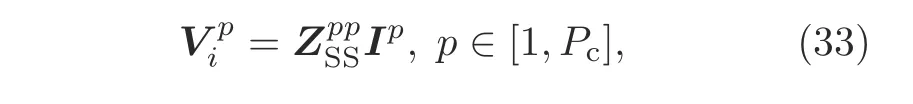
and the inner solver of the homogeneous dielectric parts solves

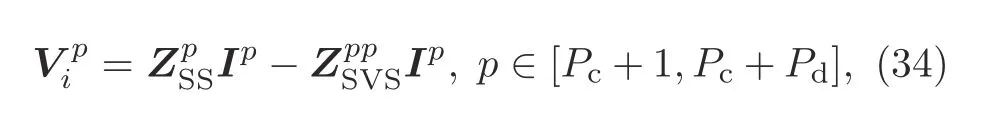
whereis the excitation vector of regionpin theithiteration process.

4.2.2 Iteration process

The coupling among different sub-regions is considered in the iteration process.In each iteration process，an additional excitation matrix ΔV pis computed for each region，and the excitation matrix of regionpin the (i+1)thiteration is calculated by

In Eq.(36)，is the current matrix of partqgained in theithiteration process andis the same asV pin Eq.(16).Due to the weak coupling among different sub-regions，the coupling matrices are of low rank.ACA(Zhao et al.，2005)can be used to compress the coupling matrices.Thus，the lowrank coupling impedance matrices in Eq.(36)can be compressed by

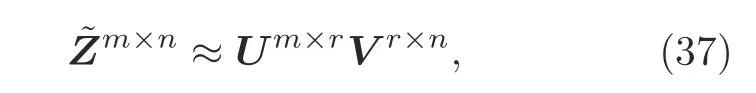
whereris the effective rank of them×nweak coupling matrixZ(r ≪m，n)，and them×rmatrixUandr×nmatrixVare dense rectangular matrices.

The iteration process will stop when the current becomes stable，and the stopping criterion is

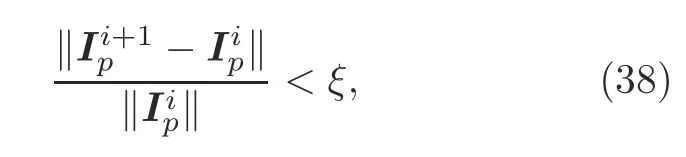
where‖·‖is the 2-norm form andξis the threshold value.

In the enhanced solution in the weak coupling case，the coupling among different sub-regions is accelerated by ACA.The ACA algorithm requiresO(rNs+rNv)=O(rNv) memory storage andO(r2Ns+r2Nv)=O(r2Nv) CPU time (Zhao et al.，2005).After matrix compression，the CPU time for constructing the additional excitation matrices is reduced toO(rNv).In addition，the computational complexity of the inner solving process is.Thus，the enhanced solution in the weak coupling case hascomputational complexity.

5 Numerical results

In this section，numerical results are presented to test the efficiency and validity of the proposed method.The following examples are performed on a personal computer with 3.70-GHz Intel®CoreTMi7-8700K CPU(six cores are used)and 64 GB RAM.The computational resource requirements of the direct solution to GME and the proposed enhanced solution for all numerical results are presented in Table 1.The number of iteration steps for the strong coupling case in Table 1 is derived from the iterative matrix equation solver，and the number of iteration steps for the weak coupling case is derived from the coupling process between different sub-regions.

Table 1 Computational resource requirements of the direct and enhanced solutions

As previously mentioned，the enhanced solution can be used to analyze the scattering characteristic of homogeneous objects.For metal objects，letPc=1 andPd=0 in Eq.(12).For homogeneous dielectric objects，letPc=0 andPd=1.Here，first，a dielectric almond shape with relative permittivity(2.0，-0.5)is analyzed.The object is discretized by 10 911 tetrahedrons，which leads to 3753 triangle pairs on its surface.The almond is illuminated by a 3.0 GHz vertically polarized incident plane wave from(θ，φ)=(0°，0°).The radar cross section(RCS)in the directionsθ ∈[0°，360°]，φ=0°is calculated.Fig.3 shows the RCS results of the enhanced solution and the results of the direct solution and the solution using the FEKO software.

Fig.3 Bistatic RCS of the almond computed by the direct solution，enhanced solution，and FEKO

Second，two examples are presented to test the accuracy and efficiency of the proposed enhanced solution in the strong coupling case.First，the analysis of a stratified ball is presented.As shown in Fig.4a，31 652 tetrahedrons discretize the ball，and 7222 triangles discretize the boundaries of the subregions in total，which leads to 10 833 unknowns.The sub-regions formed by dielectric materialsA，B，C，D，and the perfect electric conductor (PEC)sub-region contribute 1113，2307，3114，2985，and 1314 unknowns，respectively.The relative error distribution of the total field throughout the dielectric regions with respect to the FEKO solution is presented in Fig.4b.In addition，the relative error is defined by

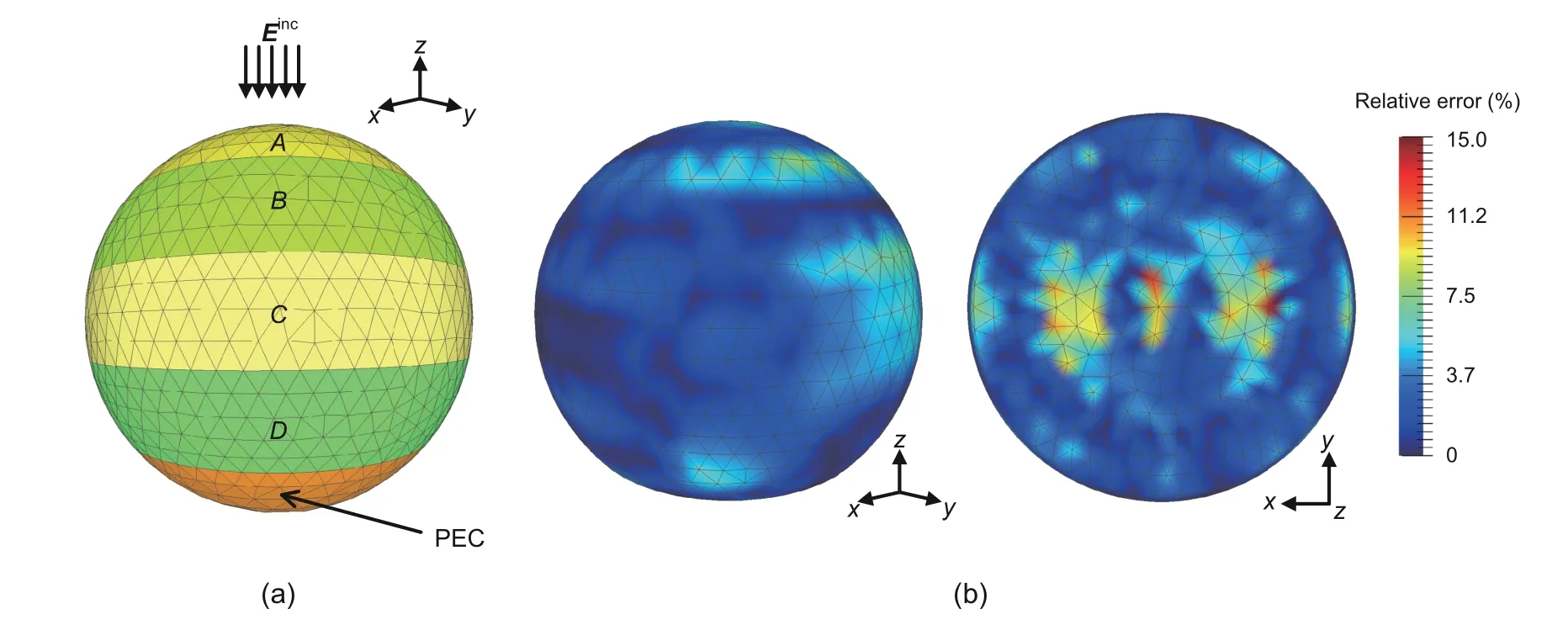
Fig.4 Model and simulation results of the stratified ball

where RE(r) is the relative error value at pointr，Ee(r) is the total field calculated by the proposed enhanced solution，andEFEKO(r) is the total field calculated by FEKO，and the norm is defined as the 1-norm form.Then，a composite ball is considered.The composite ball is discretized by 72 299 tetrahedrons，and 14 610 triangles discretize the boundaries of the sub-regions in sum，which leads to 21 915 unknowns.The sub-regions formed by the dielectric materialsA，B，C，D，E，and the PEC sub-region contribute 1935，4086，4851，5997，3972，and 1074 unknowns，respectively，as shown in Fig.5a.The total field distribution is presented in Fig.5b.The RCS in directionsθ ∈[0°，360°]，φ=0°for VV polarization calculated by the enhanced solution is in good agreement with those of the direct solution and the FEKO solution，as shown in Fig.6.

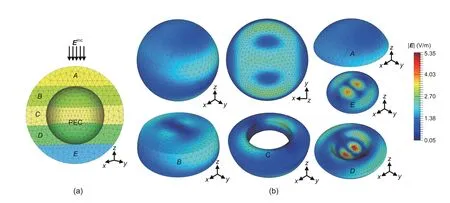
Fig.5 Model and simulation results of the composite ball

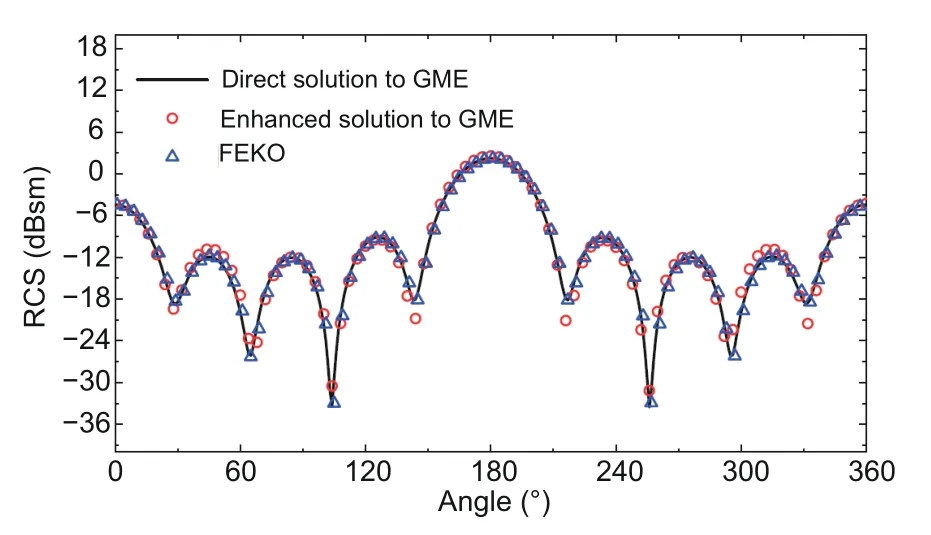
Fig.6 Bistatic RCS of the composite ball computed by the direct solution，enhanced solution，and FEKO

Third，a discrete object consisting of several discrete sub-regions is analyzed by the proposed enhanced solution in the weak coupling case.As shown in Fig.7a，the scattering target array is discretized by 74 423 tetrahedrons，and 10 276 triangles discretize the boundaries of the sub-regions in total，which leads to 15 404 unknowns.The inner PEC cube has 608 unknowns，and the dielectric balls(from the ball formed by materialA，counterclockwise)have 1119，1431，1860，2253，2589，2253，1860，and 1431 unknowns.The total field distribution is presented in Figs.7b and 7c.The RCS in directionsθ ∈[0°，360°]，φ=90°for VV polarization calculated by the proposed method is in good agreement with those of the direct solution and the FEKO solution，as shown in Fig.8.

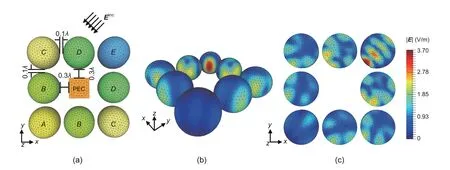
Fig.7 Model and simulation results of the discrete objects

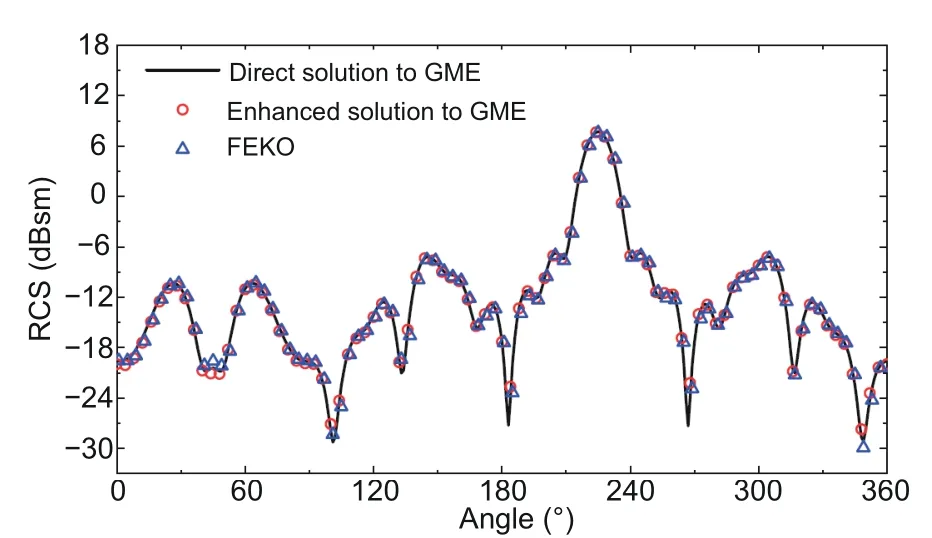
Fig.8 Bistatic RCS of the discrete object computed by the direct solution，enhanced solution，and FEKO

Compared with the direct solution to GME，the proposed enhanced solution generates results with low relative errors，and the proposed method requires only 11.6% memory and 11.8% CPU time on average among these cases.It can be concluded that the enhanced solution has better performance when analyzing homogeneous objects and composite objects compared with the direct solution.

6 Conclusions

In this paper，an enhanced solution to SVSEFIE is proposed and implemented to solve the EM scattering problems of metal–dielectric composite objects.Although SVS-EFIE can reduce the number of unknowns when analyzing homogeneous dielectric objects，it can result in complex equations，laborious implementation，and unacceptable computational complexity when it is applied to metal–dielectric composite objects.Thus，GME is first presented to analyze the metal–dielectric composite objects.Note that GME can also be used to analyze the scattering properties of homogeneous objects.Then，the enhanced solution with two policies to GME is proposed.These two policies can be selected adaptively based on the coupling degree concerning the spacing between different subregions.For the strong coupling case，the enhanced solution based on the addition theorem is proposed.For the weak coupling case，the enhanced solution based on the iterative method and algebra-based matrix compression method is proposed.In addition，CPU parallelism can be easily applied to the enhanced solution.Numerical results demonstrate that the proposed method requires only 11.6%memory and 11.8%CPU time on average compared to the previous direct solution.Numerical results demonstrate the efficiency and accuracy of the proposed method.

Contributors

Han WANG designed the research and implemented the code.Mingjie PANG and Hai LIN processed the data.Han WANG drafted the paper.Mingjie PANG helped organize the paper.Han WANG，Mingjie PANG，and Hai LIN revised and finalized the paper.

Compliance with ethics guidelines

Han WANG，Mingjie PANG，and Hai LIN declare that they have no conflict of interest.