Cooperative planning of multi-agent systems based on task-oriented knowledge fusion with graph neural networks*

Hanqi DAI，Weining LU‡，Xianglong LI，Jun YANG，Deshan MENG，Yanze LIU，Bin LIANG

1Department of Automation，Tsinghua University，Beijing 100084，China

2Beijing National Research Center for Information Science and Technology，Tsinghua University，Beijing 100084，China

3Office of Science and Technology，Tianjin University，Tianjin 300350，China

4School of Aeronautics and Astronautics，Sun Yat-sen University，Shenzhen 518107，China

5Faculty Office of Electrical and Electronics Engineering，University of Nottingham，Ningbo 315154，China

Abstract: Cooperative planning is one of the critical problems in the field of multi-agent system gaming.This work focuses on cooperative planning when each agent has only a local observation range and local communication.We propose a novel cooperative planning architecture that combines a graph neural network with a task-oriented knowledge fusion sampling method.Two main contributions of this paper are based on the comparisons with previous work:(1) we realize feasible and dynamic adjacent information fusion using GraphSAGE (i.e.，Graph SAmple and aggreGatE)，which is the first time this method has been used to deal with the cooperative planning problem，and(2)a task-oriented sampling method is proposed to aggregate the available knowledge from a particular orientation，to obtain an effective and stable training process in our model.Experimental results demonstrate the good performance of our proposed method.

Key words: Multi-agent system;Cooperative planning;GraphSAGE;Task-oriented knowledge fusion

1 Introduction

Coordination and cooperation(C&C)is defined as“joint operation or action amongst a group of agents”(López et al.，2011)，which is the essential ability required for a multi-agent system(MAS)to tackle various practical tasks.The cooperative multi-agent planning problem is one of the representative tasks that can reflect the C&C ability of MAS.Research in the area of cooperative multiagent planning has attracted wide attention among researchers and achieved remarkable progress in recent years (van den Berg J et al.，2008;Sartoretti et al.，2019).Cooperative multi-agent planning has many practical applications，such as logistics and warehousing(Wurman et al.，2007;Enright and Wurman，2011)，traffic control (Dresner and Stone，2008)，robotics (Veloso et al.，2015)，and mobilityon-demand services(Prorok and Kumar，2017).The main objective of cooperative planning is to find an efficient and effective coordination plan among autonomous agents that generates collision-free paths leading agents from their source nodes to the designated destinations.The plan should not only ensure the generation of collision-free paths，but also minimize the number of the total time steps required for every agent to reach its destination.However，it is not easy to achieve planning accuracy and calculation efficiency at the same time.Currently，the methods of cooperative planning can be generally classified as centralized and decentralized (Singhal and Dahiya，2015).Centralized coordination is realized by a planning unit that considers an MAS as a multidegree-of-freedom system.The planning unit is responsible for obtaining global information and making collaborative decisions.The decisions that are conveyed to each agent are used for real-time navigation.Centralized coordination can generally achieve optimal and complete solutions.However，this requires very expensive computation，and if the spatial dimension is large or even continuous，then the optimal strategy must be NP-hard (Standley and Korf，2011;Yu and LaValle，2013).In general，centralized coordination is not suitable for MAS with a large team due to the high computation requirement and high communication cost among the agents (Verma and Ranga，2021).Different from centralized coordination，decentralized coordination does not have a planning unit，and all agents are equivalent with respect to their responsibility to coordinate.Because there is no pressure for large-scale centralized computing，decentralized coordination significantly reduces the coupling and computational overhead.However，decentralized approaches can generally obtain only sub-optimal and incomplete solutions，and it is difficult for most of the current decentralized approaches to ensure the convergence of the negotiation process without priority planning (van den Berg JP and Overmars，2005).Therefore，balancing optimality and completeness with the complexity of computing is still an open research problem (Barer et al.，2014;Sartoretti et al.，2019).

This work focuses on cooperative planning when each agent has only local communication and a local observation range.To solve the above problem，Li et al.(2020) proposed a combined architecture that includes a convolutional neural network(CNN)(Krizhevsky et al.，2017)to fully extract features from local observations，a graph neural network (GNN) (Wu et al.，2021) to fuse features between agents，and a multi-layer perceptron (MLP)network to map a sequential action policy for every agent.The GNN provides a suitable solution because its computation is based on the graph topology，it promotes information exchange and sharing between agents，and it enhances a single agent’s perception and cognition of global information.Li et al.(2020)used the graph shift operator(GSO)(Ortega et al.，2018)left-multiply feature information matrix of neighbor nodes;however，elements on the diagonal of the GSO are all zero，and the aggregated information of the central agent is omitted，which is useful for local planning.In addition，the GSO matrix has a fixed shape and cannot be directly used for a multiagent team with a dynamic size.Furthermore，in the real world，adjacent agents，whose locations are more close to each planning agent’s goal，are likely to be more valuable in making a reasonable action decision.

Therefore，we propose a cooperative planning architecture that combines a GNN with a task-oriented knowledge fusion (TOKF) sampling method.The main contributions of the paper are as follows:

First，we use GraphSAGE (i.e.，Graph SAmple and aggreGatE) to fuse the information from adjacent agents.GraphSAGE is a GNN inductive framework that allows us to build a general model to tackle cooperative planning problems with any number of agents.

Second，we propose a TOKF sampling method to aggregate available knowledge from a particular orientation，which allows our model to achieve an effective and stable training process.

Third，promising results demonstrate the good performance of our proposed model.

2 Background

In this section，we describe the problem and then briefly review the concept and use of GraphSAGE.

2.1 Problem formulation

This is a cooperative multi-agent planning problem，in which each agent has no global positioning and has only local communication and local observations in an unknown environment.The task scene is arranged in a two-dimensional environment(W×H)with several obstacles.LetV={v1，v2，···，vN}be the set ofNagents，andN(vi) be the immediate neighborhood of agentvi，i=1，2，···，N.The perception radius of each agent isrob，and the perception range of agentviis represented asRWob×Hobon the map at timet，whereWobandHobare the width and height，respectively.The communicate radius of each agent isrcom，and the communicate network is described asG(V，Et)，whereEt ⊆V×Vis the set of edges.At timet，if(vi，vj)∈Et，agentviand agentvjcan communicate with each other.Furthermore，two agents can communicate with each other at timetin a mathematical language，that is，‖ Pi -Pj ‖≤rcom，wherePi，Pj ∈R2are the positions of agentviand agentvj，respectively.

The goal of this planning problem is to efficiently navigate the agents to their respective destinations without collision.The planned path is composed of sequential actions at each moment.Breaking down each action of the agent at timetand taking agentvias an example，we want to create a mappingFto transform the perceived informationinto a decision-making action，that is，，whereGtrepresents the communicate networkGat timet.

2.2 GraphSAGE

Based on CNN and graph embedding，GNNs have been proposed to collectively aggregate information from the graph structure(Zhou et al.，2020).GraphSAGE is a general inductive framework that uses node feature information to efficiently generate node embeddings for previously unseen data(Hamilton et al.，2017).The aggregation function is the core of the GraphSAGE framework，and it is important to design effective functions to aggregate the feature information of node neighbors on the graph.We need an aggregation function to ensure that the neural network model can be trained and applied to the feature sets of the unordered node neighborhood.

In this work，we apply the mean aggregator as the function to aggregate information.The update process is as follows:

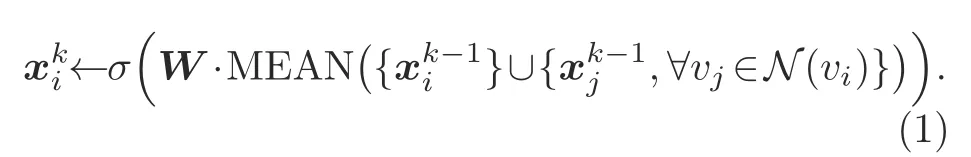
In Eq.(1)，Wis the weight matrix，k ∈{1，2，···，K}represents the layer number of the model or the“search depth，”andis the feature of agentviat layerk.The intuition behind the Graph-SAGE forward propagation algorithm is that at each iteration，agents aggregate information from their local neighbors，and as this process iterates，agents incrementally gain more and more information from further nodes of the graph (Hamilton et al.，2017).The forward propagation algorithm can be divided into three steps，and we use Fig.1 as an example for explanation.First，randomly sample neighbors in two layers.Second，from the outside to the inside，sequentially aggregate the information from the sampling agents.Third，use the aggregated information as the input of the fully connected layer to predict the target agent’s label.The overall algorithm is summarized in Algorithm 1.The input requiresG(V，E) and the features of all agents，that is，{xi，∀vi ∈V}.Whenk=1，we defineas the input feature of agentvi.Taking agentvias an example，the represented features of sampled neighborsare aggregated into a vector.Then，take the average of the input features，multiply the result by weight matrixW，and apply a non-linear activation functionσto it.The result will be used in the next step.AfterKloops，the final output at depthKis represented as.

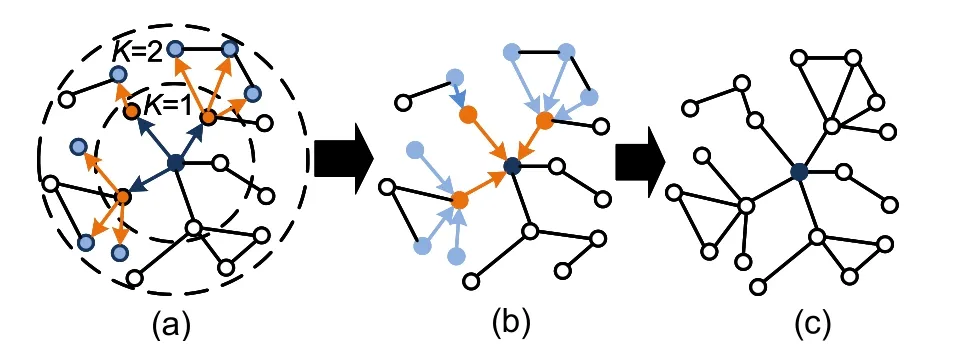
Fig.1 Illustration of the process of forward propagation:(a) sampling nodes from local neighbors;(b)aggregating feature information;(c) predicting the current state of the node

3 Proposed method

Similar to the architecture mentioned in Li et al.(2020)，we propose a three-stage method for onestep planning of each agent:(1) The environmental information extraction module learns the features from the surrounding environment.This module could be constructed using classical CNN models，such as VGGNet and ResNet.Learned features，coupled with the central agent’s own state information，could be regarded as the knowledge held by each agent，which is shared with other agents.(2) The TOKF module aggregates knowledge from adjacent agents，which is built by GraphSAGE using the task-oriented sampling mechanism.(3) The decision-making module makes an action decision with a standard MLP model.The whole structure is displayed in Fig.2.

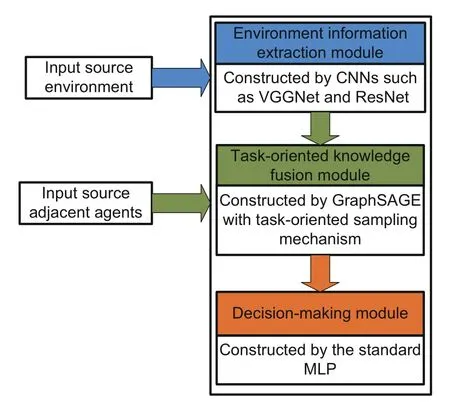
Fig.2 Structure of the proposed method for one-step planning of each agent

The environmental information extraction module and decision-making module can be directly realized with existing models.So，we do not explain their construction processes.

As mentioned in Section 2.2，during the standard GNN model training process，the adjacent information is sampled randomly from all directions.This sampling method is suitable for issues in which there are no spatial physical correlations among various nodes.However，in the practical situation，agents close to the target can provide more beneficial information for path planning tasks，and it is a more reasonable way to purposely sample information from highly task-related agents.Therefore，to enhance the effectiveness of the GNN model while solving the practical problem，we propose a novel sampling framework and its feasible methods.The following subsections detail the framework and construction algorithm.

3.1 Task-oriented knowledge fusion (TOKF)framework

The TOKF framework is designed to increase the quality of knowledge aggregation from adjacent agents，so the central agent can reach its own goal in an optimal way.Adjacent agents，who are located in the goal direction of each planning agent，are more likely to be valuable in making a reasonable action decision.Therefore，the core idea of our proposed TOKF framework is to strengthen the knowledge of agents from a particular orientation.The TOKF workflow is shown in Fig.3.Agents in the dark blue area are more helpful to the central agent in completing the path planning task than those in the light blue area.Following this idea，we introduce the realization method which uses soft sampling.

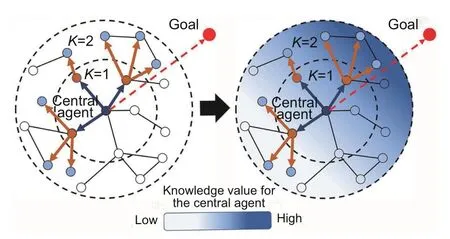
Fig.3 Workflow of the task-oriented knowledge fusion (TOKF) (References to color refer to the online version of this figure)

3.2 Soft sampling TOKF

It is not feasible to choose valuable adjacent agents by modifying only the connection weight between agents，because the chosen agents are not permanent in every training epoch.Therefore，we screen the target agents according to their own observable features，that is，their positional relationship to the central agent.First of all，we define the“towards area”and“backwards area.”A coordinate system is constructed，with the central agent as the origin，the line between the central agent and its goal as theyaxis，and the direction toward the goal as the positive direction of theyaxis.Then，in this coordinate system，the first and second quadrants are the towards area，and the third and fourth quadrants are the backwards area.These divisions are displayed in Fig.4.

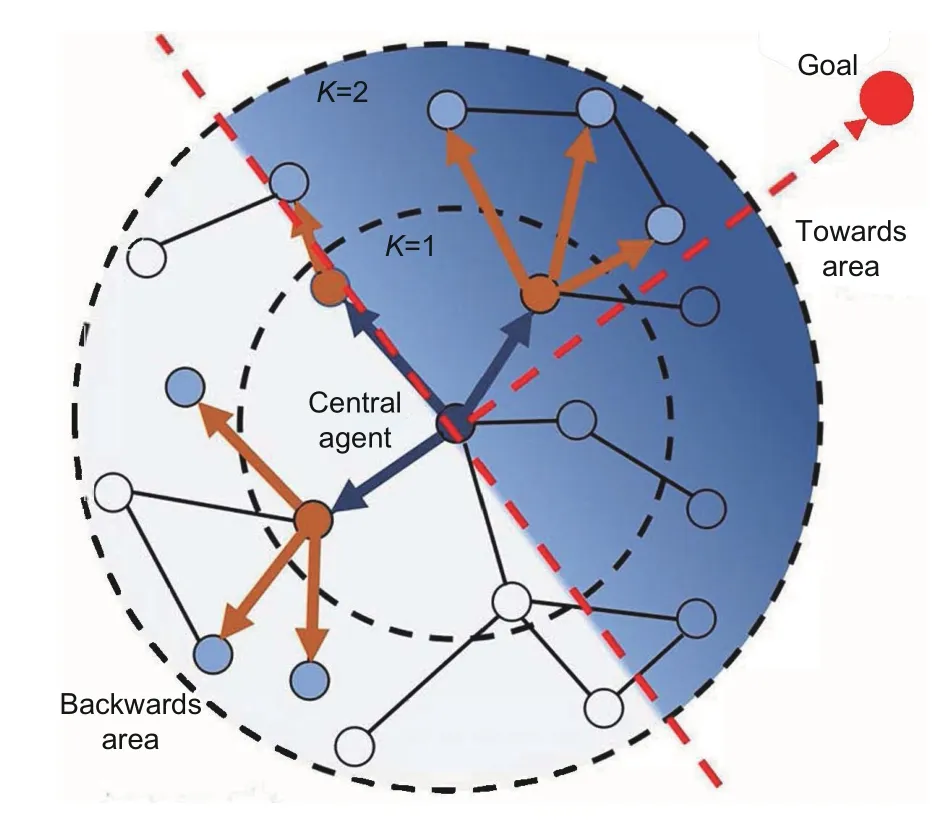
Fig.4 Definition of towards and backwards areas

We multiply the knowledge vector by a larger coefficientθtowardswhile adjacent agents are in the towards area，and a smaller coefficientθbackwardsfor those in the backwards area.It is worth noting that the soft sampling algorithm is applied only to the first-level neighbors，to avoid losing information from further invisible agents.By doing this，knowledge from valuable adjacent agents is strengthened.The TOKF-GraphSAGE forward propagation algorithm is shown in Algorithm 2.

4 Experimental results and analysis

4.1 Model structure

The model structure consists of three parts:CNN，GraphSAGE，and MLP.We use VGGNet as the CNN architecture in this work.Graph-SAGE aggregates the feature tensors within aK-hop(K=1，2，3)neighborhood.The number of samples per layer is 5，and we set 128 and 7 as the input and output dimensions of GraphSAGE，respectively.The linear soft-max layer maps the output into five motion primitives(up，left，down，right，and idle).

4.2 Experimental setup and dataset

The experimental environment and dataset were the same as those in Li et al.(2020).In this work，we used 600 different maps from the dataset.The size of each map was 20×20，70%of which were used for training (420)，15% were used for testing (90)，and 15% were used for validation (90).Our hardware platform was conducted using a 16-core，3.4 GHz i9-129 000 K CPU and an Nvidia GTX 3090 GPU with 24 GB of memory.

4.3 Performance metrics

We used the same performance metrics as in Li et al.(2020):

(1)Success rate(SR)=nsuc/nis the ratio of the number of successfull cases (nsuc) to the number of tested cases(n).In a successful case，all agents reach the destination within the specified time，without collisions.

(2)Flowtime increase=(FT-FT*)/FT*is the measurement of the gap between the actual path length(FT)and the optimal path length(FT*).The maximum allowed planning length of the predicted path of each agent is set aswhereis the optimal make-span of the solution.

4.4 Results and analysis

We applied our method to the problem of cooperative planning of multiple agents，and compared it to four methods:discrete-ORCA (a velocity-based method) (van den Berg J et al.，2011)，a combined network containing only CNN and MLP(no GNN)，a method based on GNN(K=3)(Li et al.，2020)，and a method based on GraphSAGE(K=1，2，3)which uses GraphSAGE to replace our proposed TOKF.

4.4.1 Results on map data

1.Success rate

Fig.5 shows the relationship between the success rate and the number of agents for each method.From the overall trend，as the number of agents increases，the success rate decreases.Obviously，the methods that use GNNs are significantly better than discrete-ORCA and the model that uses only CNN.As the number of communication hops increases，the success rate of the methods based on TOKF-GraphSAGE and GraphSAGE increases significantly.We can also see that with the same number of communication hops，the method based on TOKF-GraphSAGE performs slightly better than the method based on GraphSAGE，but is slightly unstable compared to the method in Li et al.(2020).After analysis，we believe that the method based on TOKF-GraphSAGE filters out invalid information and significantly improves search efficiency and effectiveness;however，it still aggregates more redundant information compared to the method in Li et al.(2020).

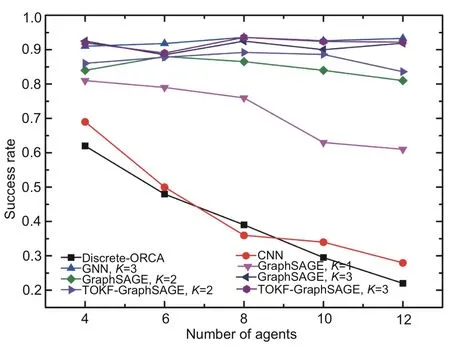
Fig.5 Success rate of various methods

2.Flowtime increase

Fig.6 shows the relationship between the flowtime increase and the number of agents for each method.From the overall trend，as the number of agents increases，the flowtime increase curve rises.Compared with the benchmark and the model that uses only CNN，we can see that the methods that use GNNs have obvious advantages.As the number of communication hops increases，the flowtime increase of the methods based on TOKF-GraphSAGE and GraphSAGE decreases significantly.With the same number of communication hops，the method based on TOKF-GraphSAGE performs slightly better than the method based on GraphSAGE and the method in Li et al.(2020).This phenomenon can be attributed to more effective information aggregation by TOKF-GraphSAGE.

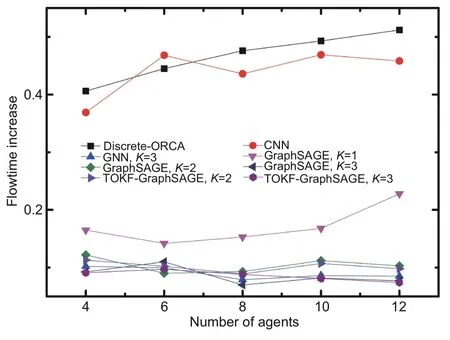
Fig.6 Flowtime increase of various methods

4.4.2 Empirical analysis

To further demonstrate the advantage of TOKF-GraphSAGE，we analyzed its performance from two perspectives:success rate with increased training epochs and learning efficiency.We visualized the learning curves of GraphSAGE(K=3)and TOKF-GraphSAGE (K=3).For clarity，we chose the success rate vs.the training epoch to show the learning process，as shown in Fig.7.Two phenomena are worthy of attention:(1)TOKF-GraphSAGE can achieve a better success rate with fewer training epochs than GraphSAGE (the red curve is always above the black curve).This indicates that our proposed TOKF aggregates more useful knowledge from adjacent agents.(2) The learning curve of TOKF-GraphSAGE is more stable than that of GraphSAGE;specifically，the red curve keeps increasing and the black curve drops at approximately 40 training epochs.We suggest that the knowledge from agents in the outer area might mislead the action policy evolution process.

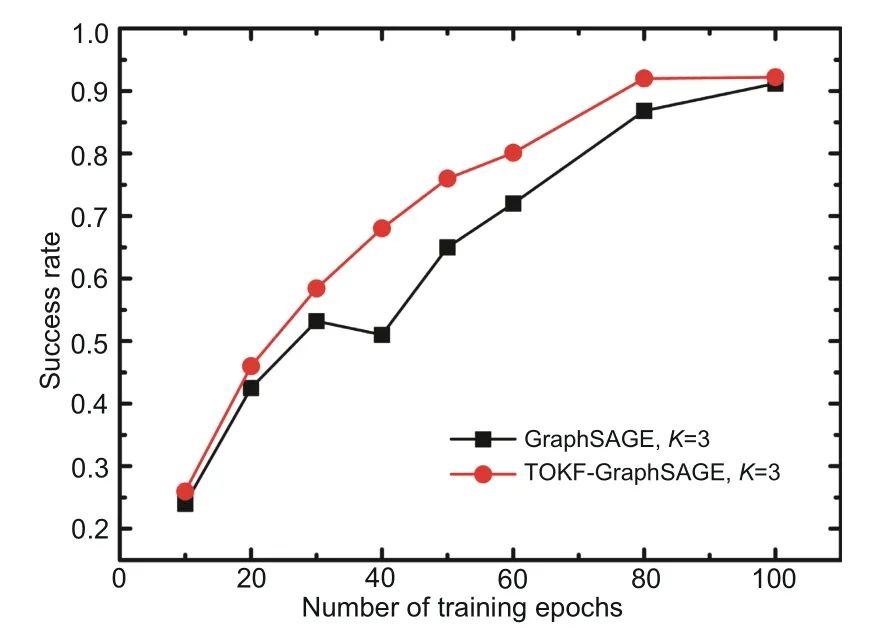
Fig.7 Learning curve comparison between the GraphSAGE and TOKF-GraphSAGE (References to color refer to the online version of this figure)

In addition to the comparison of success rates obtained with the same number of training epochs，learning speed is crucial for performance evaluation.Therefore，we compared learning efficiency between GraphSAGE (K=3) and TOKF-GraphSAGE(K=3).The significant advantage of TOKFGraphSAGE can be seen clearly in Fig.8.TOKFGraphSAGE completed the training process of 100 epochs in 7 h，whereas GraphSAGE took nearly 20 h to complete the same training process.

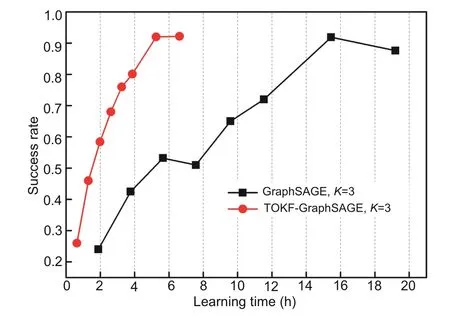
Fig.8 Learning time comparison between the Graph-SAGE and TOKF-GraphSAGE

We list the soft sampling parametersθtowardsandθbackwardsin Table 1.The results are in agreement with our hypothesis，θtowards(0.506)＞θbackwards(0.312).This means that the knowledge from towards area agents is more important for cooperative planning than that from backwards area agents，and the effectiveness of our proposed TOKF is demonstrated.

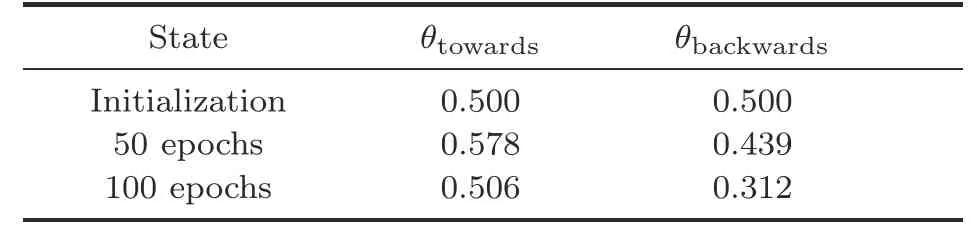
Table 1 Values of θtowards and θbackwards

4.4.3 Generalization ability analysis

As stated earlier，one of the prominent advantages of our proposed model is that it is generalizable.This means that the learned model can be used to handle cooperative planning problems involving various numbers of agents and map sizes.To analyze this ability，we observed various numbers of agents (20，30，40，50，and 60) and various map sizes (10×10，15×15，20×20，25×25，and 30×30).The baseline model was trained in an experimental setup of 10 agents and a 20×20 map size.For other experimental conditions，we chose the best performance within 100 training epochs.

For clarity，we calculate the decrease rate (DR)of success rate with the following formula:

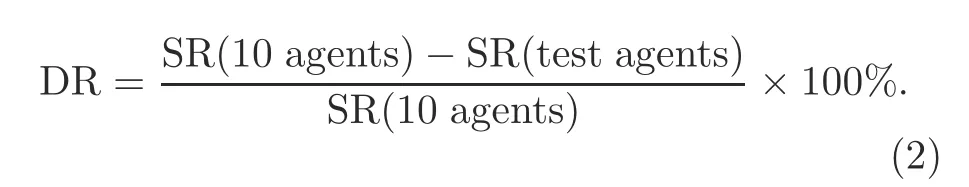
The results for the agent number variation are shown in Fig.9.As the number of agents increases，the success rate begins to decrease with a tolerable cost(a maximum reduction of 10.82%).In a map of limited size，the possibility of agents being blocked from reaching the goal is increased.

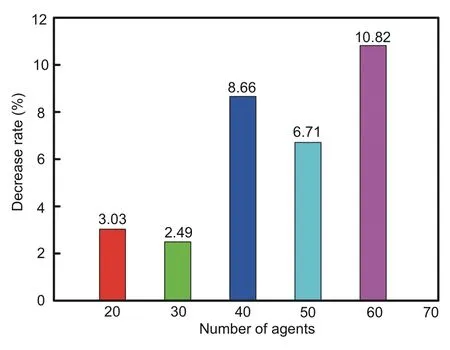
Fig.9 Generalization on various numbers of agents

Table 2 presents the experimental results with various map sizes.The results prove that the trained model could deal with maps of unknown size(a maximum reduction of 3.14%)，because our model successfully learns the path planning policy using only local information.For smaller-size maps，it is easier to find the correct path to the goal.It takes longer to find the correct path in larger-size maps.The time required might exceed the maximum planning time length defined previously，which has a negative effect on the success rate.

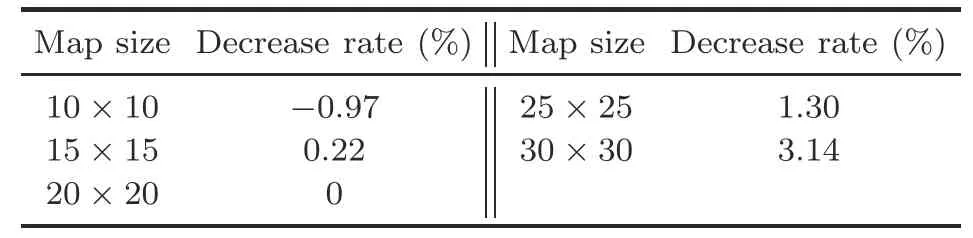
Table 2 Generalization on various map sizes

5 Conclusions

Aiming at the more complex real-world scenarios of cooperative multi-agent planning，in which each agent has a limited range of observation and communication in an unknown environment，we proposed a network architecture consisting of a CNN，TOKF-GraphSAGE，and MLP，which aggregates more effective information with a high degree of task relevance and eliminates some redundant information irrelevant to tasks.Because applying a scenario involving the current similar methods is relatively simple，in the future we plan to optimize the model so that it can be applied to more complex real scenarios.

Contributors

Hanqi DAI and Weining LU designed the research.Hanqi DAI and Weining LU conducted the experiments and drafted the paper.Xianglong LI，Jun YANG，and Yanze LIU helped organize the paper.Deshan MENG，Yanze LIU，and Bin LIANG revised the paper.Hanqi DAI and Weining LU finalized the paper.

Compliance with ethics guidelines

Hanqi DAI，Weining LU，Xianglong LI，Jun YANG，Deshan MENG，Yanze LIU，and Bin LIANG declare that they have no conflict of interest.