自适应辅助分类器生成式对抗网络样本生成模型及轴承故障诊断

杨光友 刘 浪 习晨博

1.湖北工业大学农机工程研究设计院，武汉，4300682.湖北省农机装备智能化工程技术研究中心，武汉，430068

0 引言

设备运行监测数据中，正常数据占大多数，故障类数据较少，因此数据集中的正常数据与故障数据比例严重失衡，此种情形下训练的故障诊断模型的诊断准确率较低，影响模型的可用性[1]。针对不均衡样本的故障诊断，杨宇等[2]通过少量已知样本建立多变量预测模型，对未知样本进行分类，计算已知样本与已分类未知样本的互相关性，选出相关性较高的样本作为模型训练数据集。陶新民等[3]提出的最大软间隔支持向量域描述(maximum soft margin-support vector domain description，MSM-SVDD)模型能充分利用少数故障类样本信息，将SVDD的分类边界逐渐向稀缺故障类倾斜，进而提高算法对少样本数据的敏感性，提高模型的诊断准确率。

优异的数据生成模型是解决样本不均衡问题的一种有效方法，其中比较常见的合成少数类过采样技术(synthetic minority oversampling technique，SMOTE)[4]在采样样本的K个近邻中的随机样本后插值生成新数据。RAGHUWANSHI等[5]将SMOTE生成数据与类特定极限学习机(class specific extreme learning machine，CSELM)结合来解决样本不均衡问题。ZHANG等[6]提出一种结合过采样方法与DAE(deep auto-encoder)方法的故障诊断方法，使用少数样本加权法对数量占比较低的类别进行过采样，并与真实数据混合，然后再采用DAE方法提取混合后数据的深层次特征，并将其输入至决策树进行数据分类。

生成对抗网络(generative adversarial network，GAN)[7]的核心思想是建立不断对抗的生成网络与判别网络，并迫使它们在空间分布上接近，进而生成质量较好的生产数据样本，可用于轴承故障诊断[8]。王俊等[9]提出了一种基于SDAE-GAN(stacked denoising auto-encoder GAN)的数据生成模型，SDAE在输入层添加噪声进行编码重构，使GAN模型的生成器可以提取更深层次的故障特征，提高模型的抗噪能力。

不均衡样本的故障诊断研究中，对如何平衡判别器与生成器之间的性能、加快GAN收敛的研究较少，因此笔者提出一种基于SA-ACGAN(self-adaptive auxiliary classifier GAN)的轴承故障样本生成方法，通过度量判别器与生成器之间的相对性能来自适应调节生成器的损失值。试验结果表明，本文方法大幅提升了生成数据的质量，且最终训练出的普通BP故障诊断模型性能与其他需要复杂计算方法的模型性能相当，但在诊断耗时方面，本文所提方法显著优于其他方法。

1 生成对抗网络及其改进

1.1 GAN和ACGAN模型

GAN主要由生成器网络和判别器网络组成，其结构如图1a所示，其中，随机向量z输入至生成器网络G(z)，并将z解码为生成数据Xfake，生成器网络损失函数为

(1)

式中，m为每批次训练样本数量；i为样本编号；D(*)表示判别器网络。

判别器网络判定输入数据是真实数据的概率，其损失函数为

(2)

式中，xi为该批次的第i个真实样本。

原始GAN模型只能生成不含标签的样本数据，不适宜参与实际故障诊断的有监督模型训练。图1b所示的ACGAN[10]对原始GAN添加辅助分类器，在生成器训练过程中引入标签，由判别器的交叉熵损失函数约束生成器根据标签生成数据。

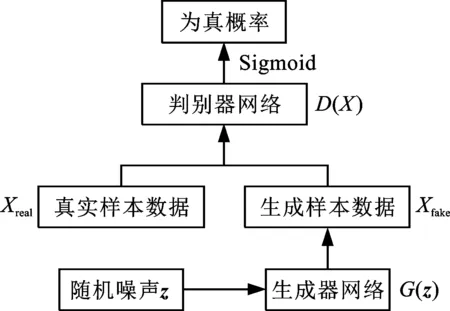
(a)GAN模型结构图

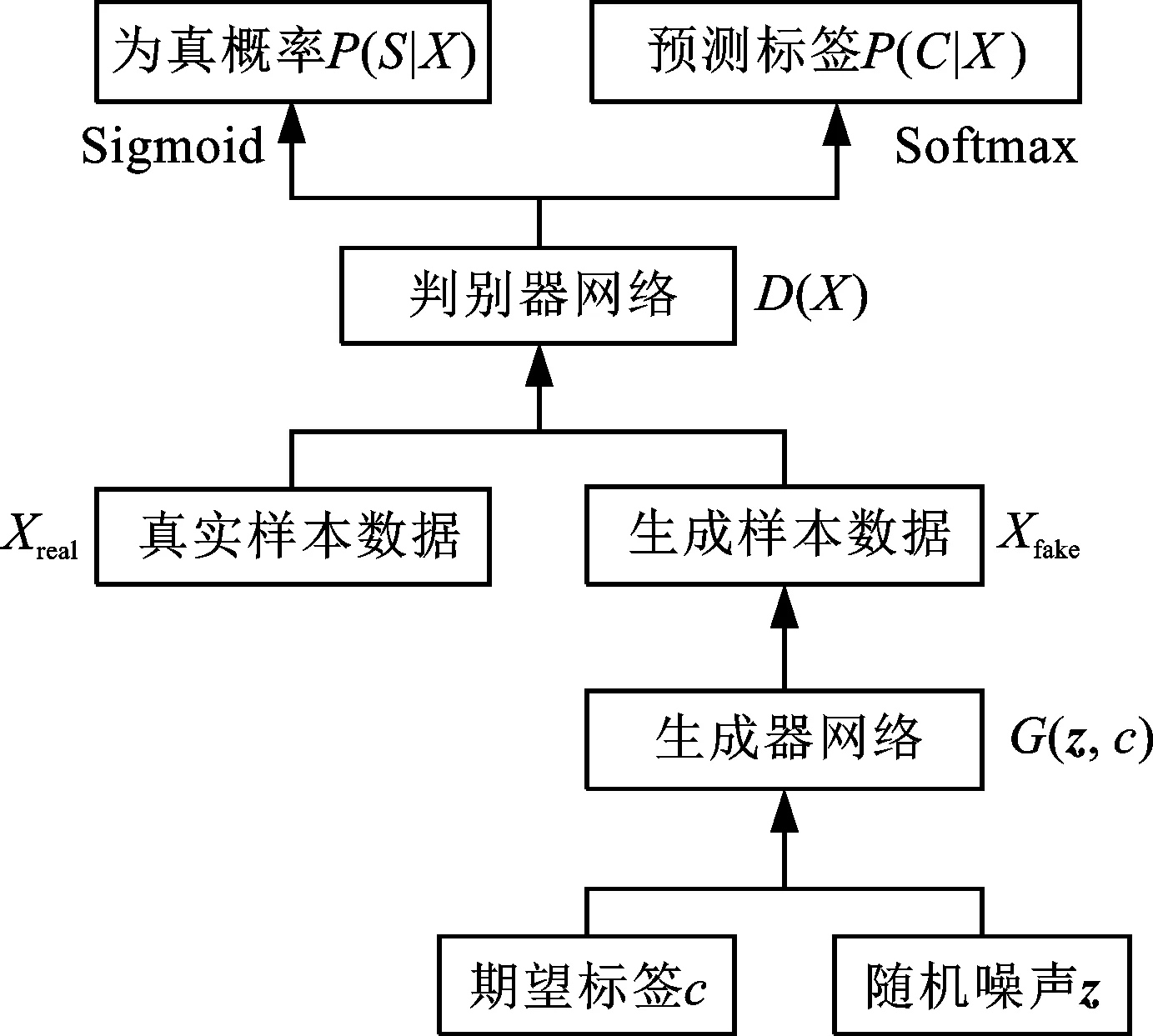
(b)ACGAN模型结构图注：图中sigmoid与softmax为相应激活函数。图1 GAN和ACGAN模型结构图Fig.1 Structure of GAN and ACGAN model

ACGAN模型训练中，通过随机采样低维度随机噪声信号z和期望标签c输入到生成器网络，再经非线性映射函数G(z，c)解码为生成数据样本Xfake；并将真实数据样本Xreal与Xfake输入至判别器网络D，判别器网络输出数据为真实样本的概率P(S|X)与所属数据类别概率P(C|X)，其中，S表示样本真假，C表示样本类别。

在判别器训练过程中，当判别器输入为Xreal时，希望判别概率P(S=real|Xreal)尽可能地大，且对输入样本的分类概率P(C|Xreal)尽可能正确；判别器输入为Xfake时，希望判别概率P(S=fake|Xfake)尽可能大。在生成器训练过程中，希望生成数据Xfake送至判别器的判别概率P(S=real|Xfake)尽可能大，迫使生成数据与真实数据在判别器的判别结果上表现一致。对应的判别器损失函数Ld和生成器损失函数Lg分别为

Ld=E(log2P(S=real|Xfake))+E(log2P(S=

fake|Xfake))+E(log2P(C=c|Xreal))+

E(log2P(C=c|Xfake)

(3)

Lg=E(log2P(S=real|Xfake))+

E(log2P(C=c|Xfake))

(4)

式中，E(*)表示期望。

1.2 SA-ACGAN模型

GAN最大的特点在于将静态优化问题转换为生成器与判别器的动态优化问题，通过判别器与生成器两者的交替训练使生成器与判别器性能达到纳什均衡，此时的判别器无法有效分辨真实样本与生成样本。

对抗训练模式能使生成的样本分布逼近真实分布，却使GAN模型不稳定，导致生成器与判别器性能不匹配等问题。生成器性能太好，判别器性能不足以支撑其与生成器形成相抗衡的对抗学习状态，导致模型收敛缓慢；判别器性能太好，会使生成器无论怎么训练，生成数据判别为真的概率始终为0，生成器的损失梯度消失，生成器性能差。解决此问题的常用优化方法有：使生成器与判别器采用不同学习率[11]、调节生成器与判别器的训练次数[12]等。这些方法通过人工调节，希望判别器与生成器达到一个较好的平衡，但忽略了判别器与生成器的性能差异是动态的，上述方法仍难使两模型同时达到收敛。

针对上述问题，笔者提出了一种自适应的生成器损失函数：

(5)

式中，ξ为平滑系数；α为变化幅度系数。

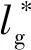
引入平滑系数ξ是为了防止D(G(z))过小导致ω过大；变化幅度系数α可使判别器性能与生成器性能相差较大时的ω变化更大，加快训练收敛速度。ω一般取2。将ω应用到ACGAN后的生成器损失函数为

E(log2P(C=c|Xfake))

(6)

2 基于SA-ACGAN的故障诊断模型及应用

基于SA-ACGAN的故障诊断流程如图2所示。离线训练阶段完成SA-ACGAN模型训练后，通过训练好的SA-ACGAN模型进行样本扩充，并将扩充后的样本数据集输入BP网络来训练故障诊断模型。在线诊断过程仅需使用训练好的BP网络进行故障诊断，SA-ACGAN模型的训练流程如图3所示。

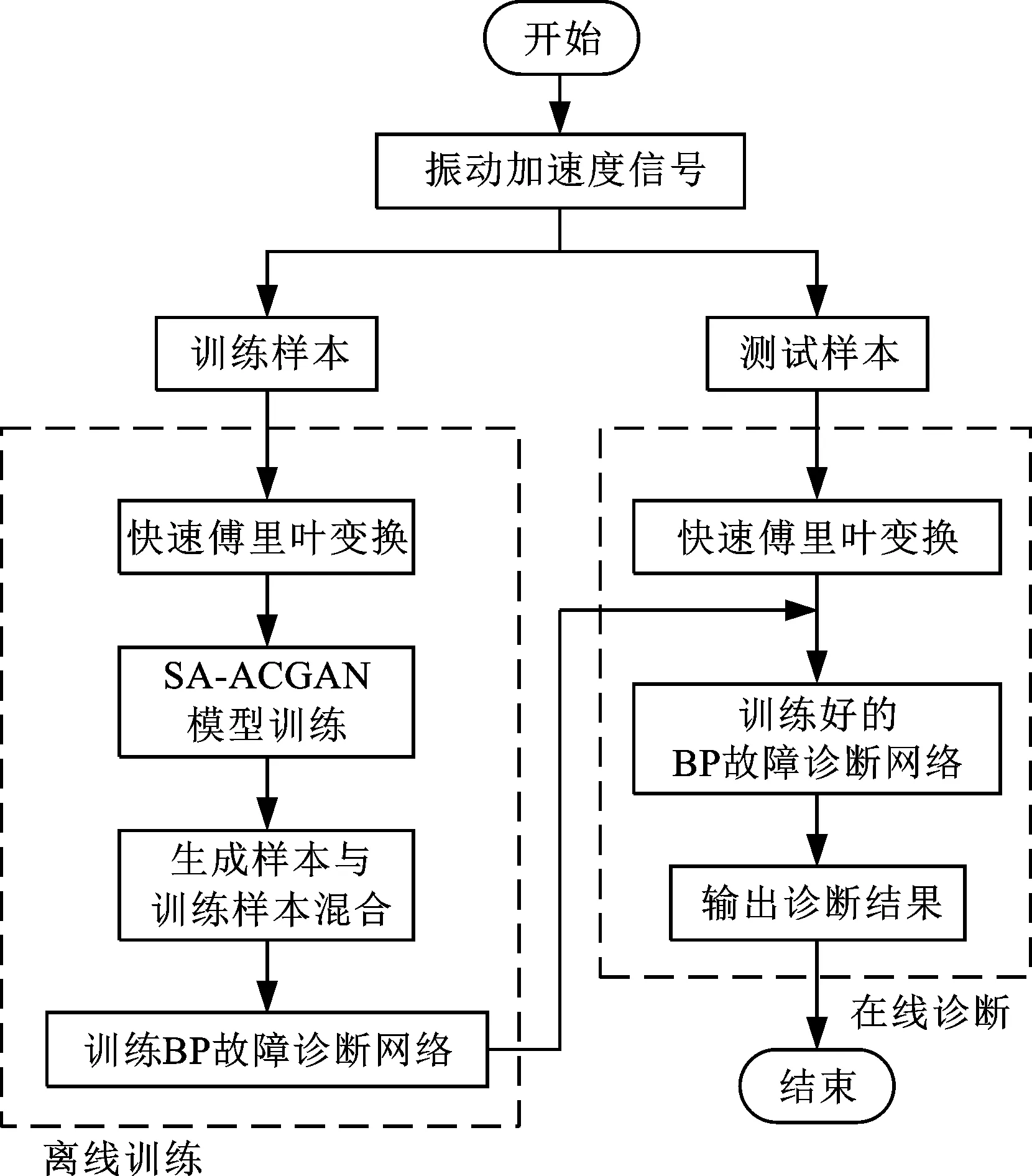
图2 故障诊断流程图Fig.2 Flow chart of fault diagnosis process

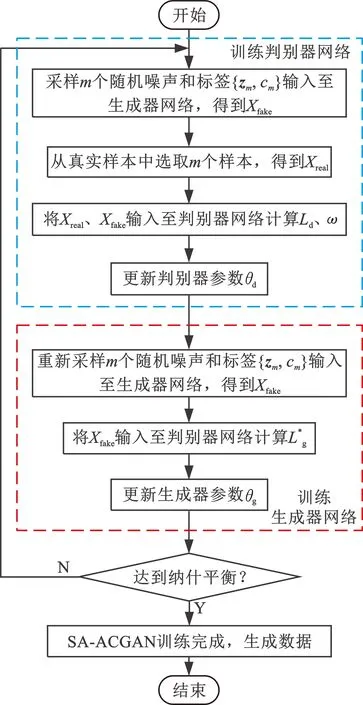
图3 SA-ACGAN训练流程图Fig.3 Training flow chart of SA-ACGAN

SA-ACGAN训练过程中，将ω的计算放在判别器网络训练既可以减小计算量，又能保证判别器的性能优于生成器的性能，提高算法的收敛效率。

为验证本文方法的有效性，采用两个数据集进行试验验证，其中，数据集1为凯斯西储大学( Case Western Reserve University，CWRU)的滚动轴承数据集，数据集2为笔者在某联合收割机脱粒滚筒实验平台采集的轴承故障数据。

2.1 试验1

2.1.1CWRU数据集

实验轴承为驱动端6205-2RS JEM型深沟球轴承，通过电火花技术在轴承内圈、外圈以及滚动体分别加工不同程度的11类故障。加速度传感器部署在驱动端电机支撑轴的轴承座上方。试验转速为1772 r/min，信号的采样频率为12 kHz。

试验数据为一维振动数据，将每2048个采样点对应数据作为一个样本，正常样本的截取间隔为32个采样点，以获得大量正常样本，故障样本也是由2048个采样点对应数据组成的样本，但其截取间隔为2048个采样点。试验数据样本训练集OA1、测试集1(由未参与训练的样本组成)、通过ACGAN得到的生成集GA1、通过SA-ACGAN得到的生成集GB1如表1所示。SA-ACGAN模型结构如表2所示。

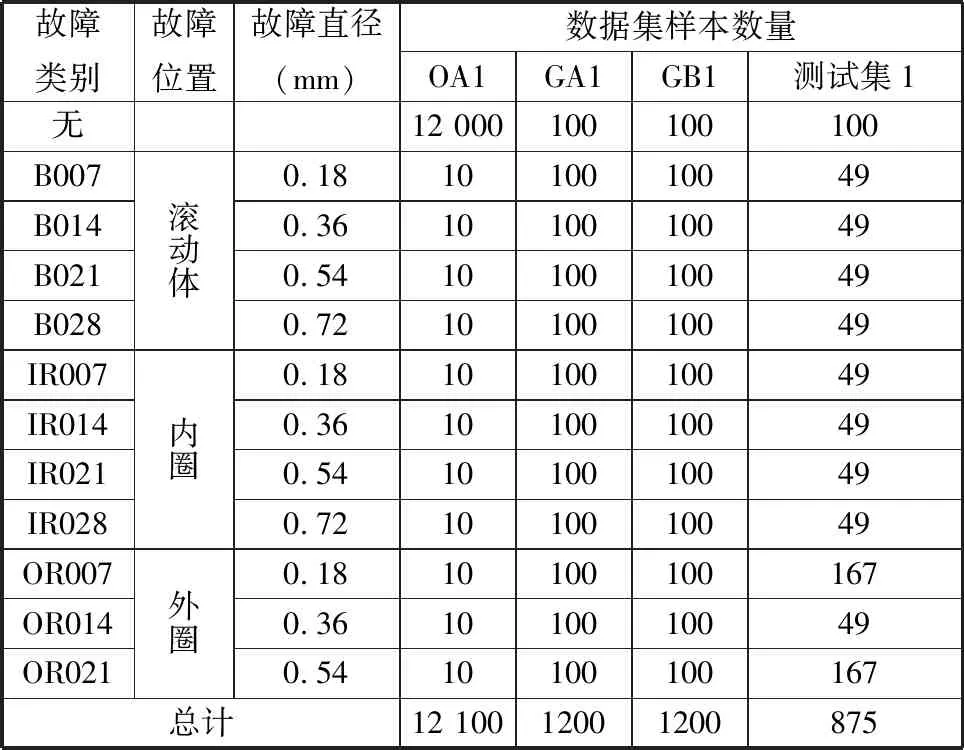
表1 CWRU数据集试验设置

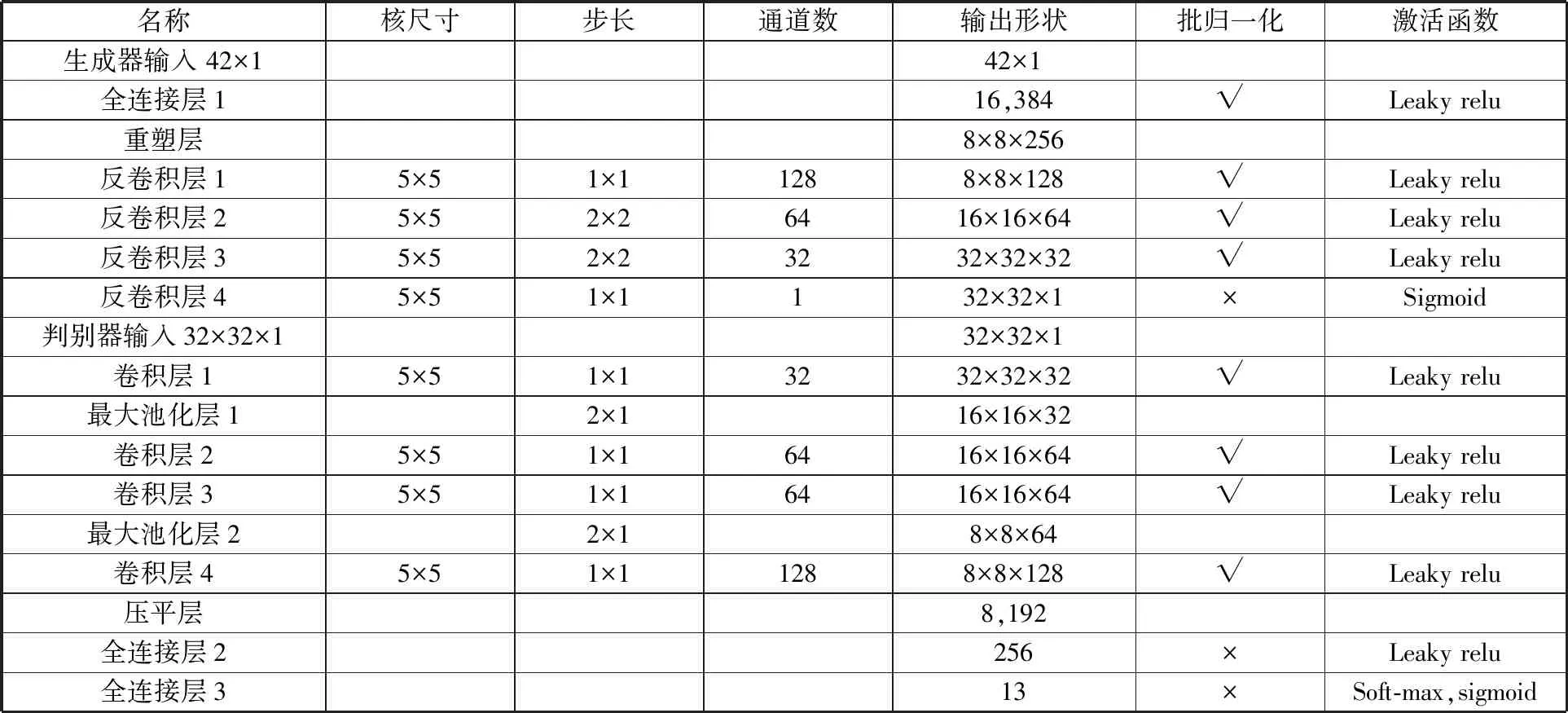
表2 SA-ACGAN模型结构表

生成器输入由随机噪声向量(长度为30)与one-hot编码后的样本标签向量(长度为12)拼接而成。由于判别器输入层形状为32×32×1，故生成器生成的样本和真实样本在训练过程中，将以32×32×1的张量形状输入到判别器中；又由于故障诊断模型输入层的形状为1024×1的向量，故在故障诊断模型训练时，需将生成器生成的样本转换为1024×1的向量后再输入到故障诊断模型中。为保证实验的一致性，ACGAN和SA-ACGAN使用同一结构，生成器与判别器均采用RMSprop优化器，学习率设为0.0001。为加快模型收敛，所有的核参数初始化方式均为He Normal初始化[13]。由1.2节可知，平滑系数ξ取较大值时，ω更稳定；ξ取值较小时，ω变化区间大，对生成器和判别器的性能修正效果好，但会导致ω出现大幅度震荡，引起模型坍塌等问题，因此变化幅度系数α取值不宜超过3。后续试验中，平滑系数ξ取值为1，变化幅度系数α取值为2，此时ω的取值范围是0.25～4.00，在此取值条件下，模型训练收敛快且稳定。

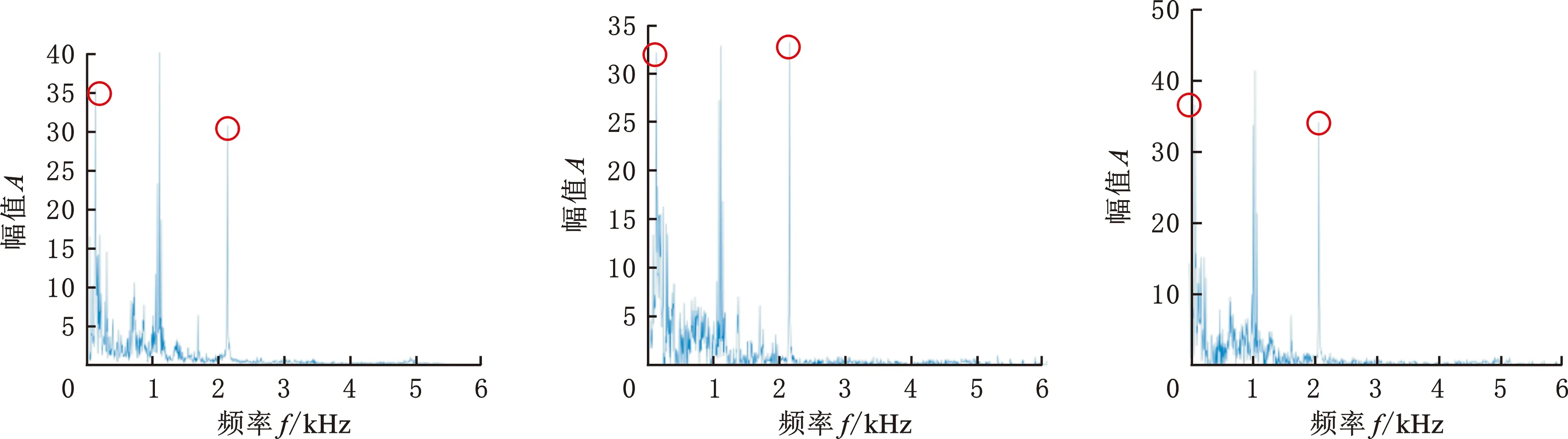
(a)正常轴承真实数据频谱图 (b)ACGAN生成正常 轴承数据频谱图 (c)SA-ACGAN生成正常轴承数据频谱图

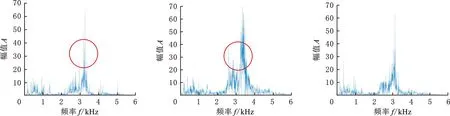
(d)滚动体故障轴承真实数据频谱图 (e)ACGAN生成滚动体 故障轴承数据频谱图 (f)SA-ACGAN生成滚动体故障轴承数据频谱图

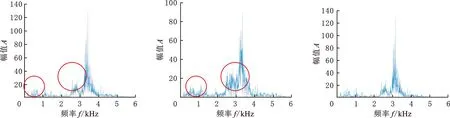
(g)外圈故障轴承真实数据频谱图 (h)ACGAN生成外圈故障轴承数据频谱图 (i)SA-ACGAN生成外圈故障轴承数据频谱图图4 真实样本与生成样本对比图Fig.4 Comparison of real samples and generated samples

图4为部分真实样本与生成样本的频谱图，可以看出，图4a(正常轴承频谱)中，100 Hz和2000 Hz处的幅值左大右小；图4b中，100 Hz和2000 Hz处的幅值相近；图4c中，100 Hz和2000 Hz处的幅值左大右小，显然本文方法生成数据的频谱特征更接近原始数据的频谱。在滚动体故障频谱图中，图4d的主频单峰值特征明显；图4e主峰的毛刺较多，且在3000 Hz左侧的频谱分布明显与原始数据图谱不同；图4f与图4d的频谱分布相似。对于外圈故障，图4h中，3000 Hz左边的毛刺较多，且主频3500 Hz处的幅值与真实样本的幅值相差太大，图4i与图4g的频率分布接近。由此可知，SA-ACGAN的细节学习能力要强于ACGAN，生成的数据更接近真实数据。

故障诊断使用的BP网络结构如表3所示，其输入为预处理后的一维加速度信号，输出对应表1的12种轴承状态。

2.1.2试验结果及分析

分别使用数据集OA1、数据集OA1+生成集GA1、数据集OA1+生成集GB1训练BPNN，用测试集1测试的故障识别平均准确率如表4所示，其中，GA1、GB1分别由ACGAN和SA-ACGAN生成。

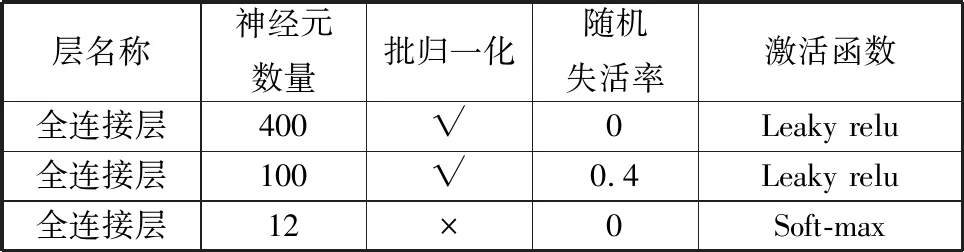
表3 故障诊断模型结构表

由表4可知，仅使用原始样本数据集OA1训练的模型故障诊断准确率为22.45%～100.00%，模型性能差且不稳定，B021的识别率仅为22.45%；使用数据集OA1+生成集GA1训练的模型故障诊断的平均准确率为96.23%，较OA1的平均准确率84.10%有大幅提高，并且模型的稳定性有了较大的提高，且整体鲁棒性提升较大；数据集OA1+生成集GB1训练的模型故障识别平均准确率达到了99.66%，除复合故障OR007的识别准确率为98.20%外，其余均为100.00%，该方法不仅能大大提高故障诊断模型的识别准确率，且还能提高模型稳定性和鲁棒性。

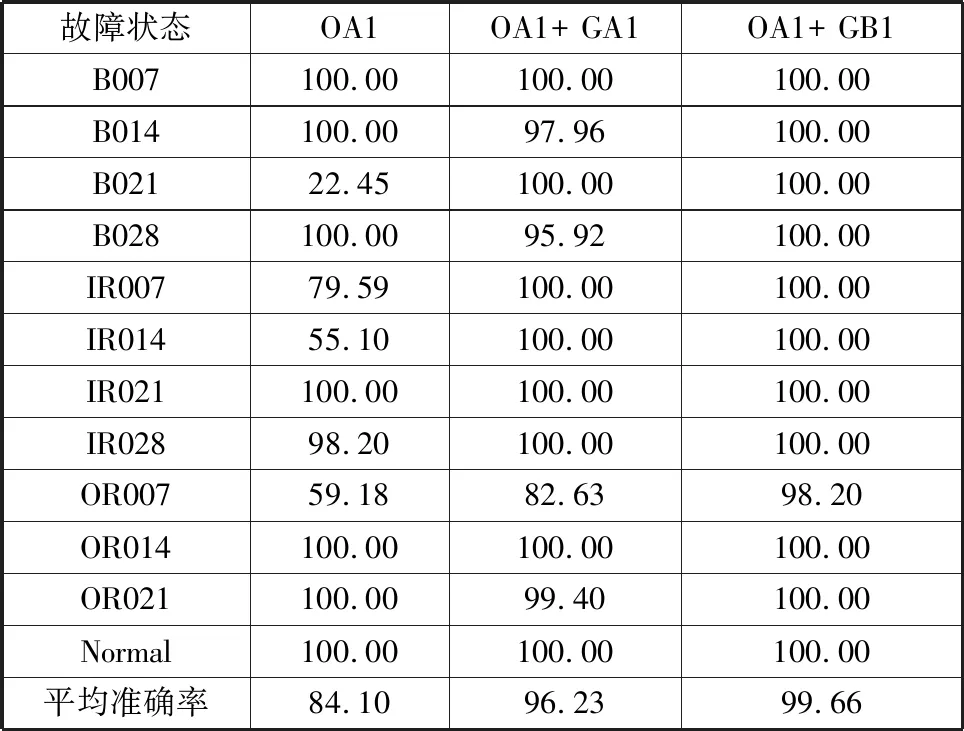
表4 各类故障准确率

2.2 试验2

2.2.1试验数据

试验平台主要由电机驱动部分、脱粒总成部分、数据采集部分以及上位机组成。试验监测对象为联合收割机脱粒滚筒后端的6307深沟球轴承，通过更换带有不同故障的深沟球轴承来模拟轴承不同的工作状态(表5和图5)。试验中，通过4个CT1010L加速度传感器采集轴承在不同工作状态、不同位置的加速度信号，加速度传感器1～4的电压灵敏度分别为101.6 mV/g、99.1 mV/g、101.2 mV/g和101.3 mV/g，实验平台以及加速度传感器布置位置如图6所示。

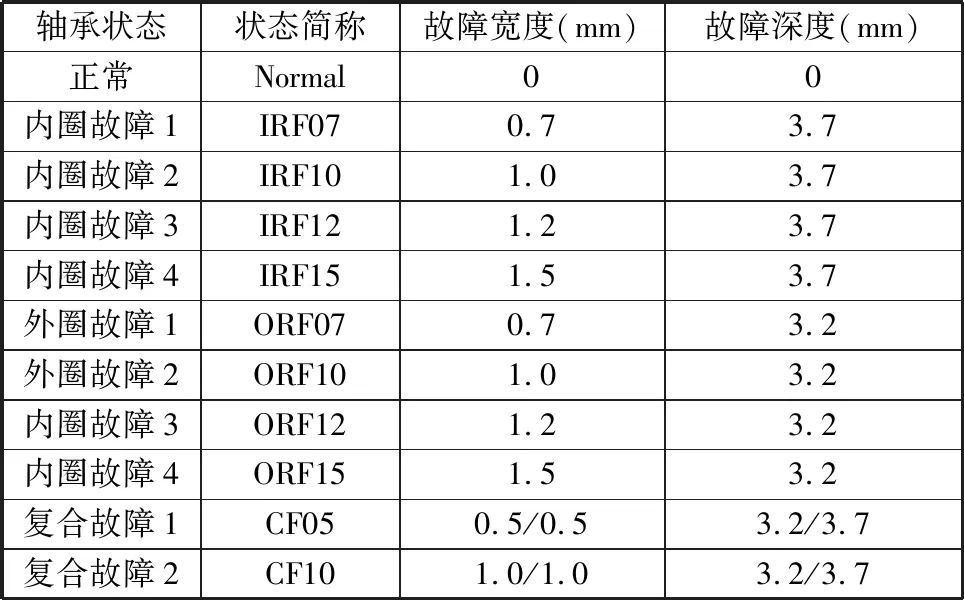
表5 不同状态参数表

本试验数据为4通道振动数据，工作转速为320 r/min，将2048个采样点的对应数据作为一组样本，样本截取间隔为1024个采样点。数据样本集OA2、生成集GA2、生成集GB2所构成的样本不均衡试验数据集如表6所示，其中，GA2、GB2分别由ACGAN和SA-ACGAN生成。

试验所使用的生成对抗网络模型与表2相似，由于总计类别为11类、通道数为4，故生成器的输入形状为41×1，输出层(反卷积层4)的通道数改为4；判别器网络输入形状为32×32×4，输出神经元12个，其中，11个神经元对应表5的11种轴承状态，1个神经元对应判别器判别结果的概率。故障诊断BP网络模型与表4相似，输入形状为1024×4，输出层神经元个数为11。优化器、学习率以及其他超参数均与2.1.1节保持一致。

(e)IRF15 (f)ORF07 (g)ORF10 (h)ORF12

(i)ORF15 (j)CF05 (k)CF10图5 不同故障类型轴承Fig.5 Different type of bearing

图6 联合收割机试验平台传感器安装示意图Fig.6 Schematic diagram of sensor installation of combine harvester test platform

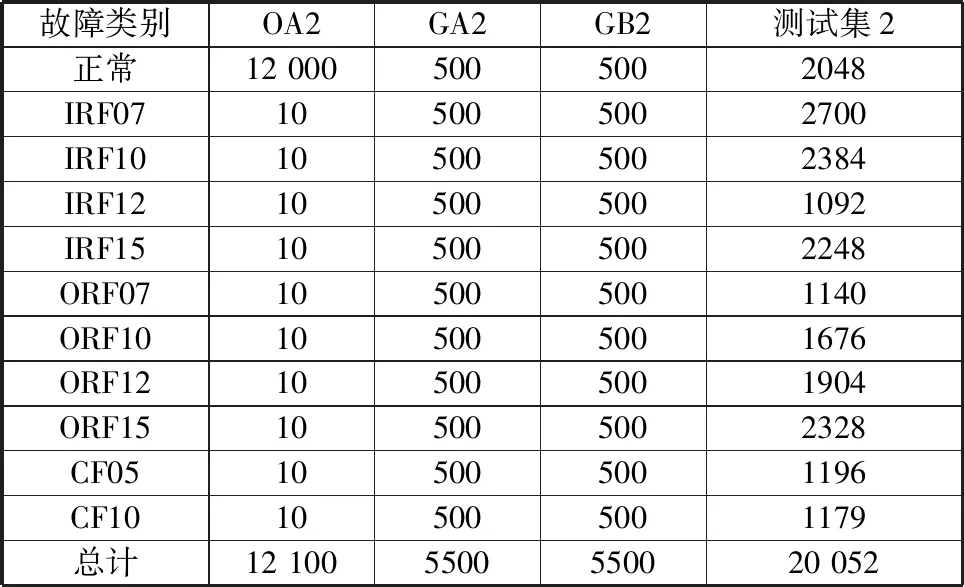
表6 不均衡试验数据集设置

2.2.2试验结果及分析

分别使用数据集OA2、数据集OA2+生成集GA2、数据集OA2+生成集GB2训练BPNN，同时用测试集2检验BPNN每轮训练结果。图7为不同故障的准确率随模型训练次数变化的曲线。由图7可知，数据集OA2+生成集GB2训练的模型收敛最快、平稳性最好。

3个数据集训练的故障诊断模型的分类准确率如表7所示。由表7可知，使用数据集OA2训练的故障诊断模型的平均准确率为94.70%，由于故障样本不均衡，故障分类准确率波动很大，对特征难以提取的故障的分类准确率较低，如内圈故障ORF12、复合故障CF10的分类准确率仅为80.67%和73.27%。使用数据集OA2+生成集GA2训练的模型故障分类准确率平均为98.67%，但ORF15的识别率(单个故障分类准确率的最小值)为92.66%，IRF10识别率为95.05%。使用数据集OA2+生成集GB2训练模型生成的样本质量更稳定，整体分类准确率达到了99.90%；单个故障分类准确率的最小值为99.33%，对CF10、ORF12的识别准确率为100.00%和99.95%。

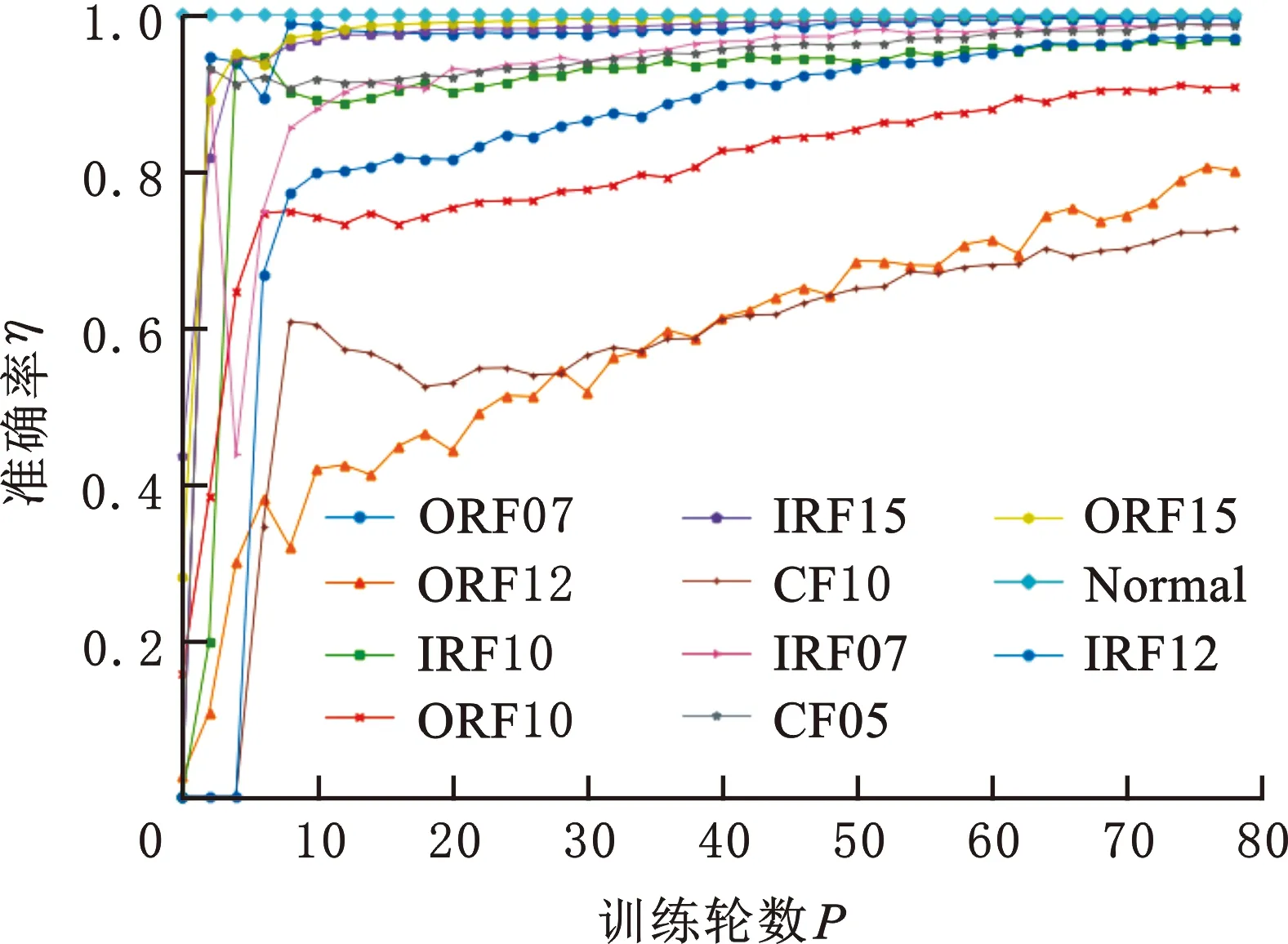
(a)数据集OA2

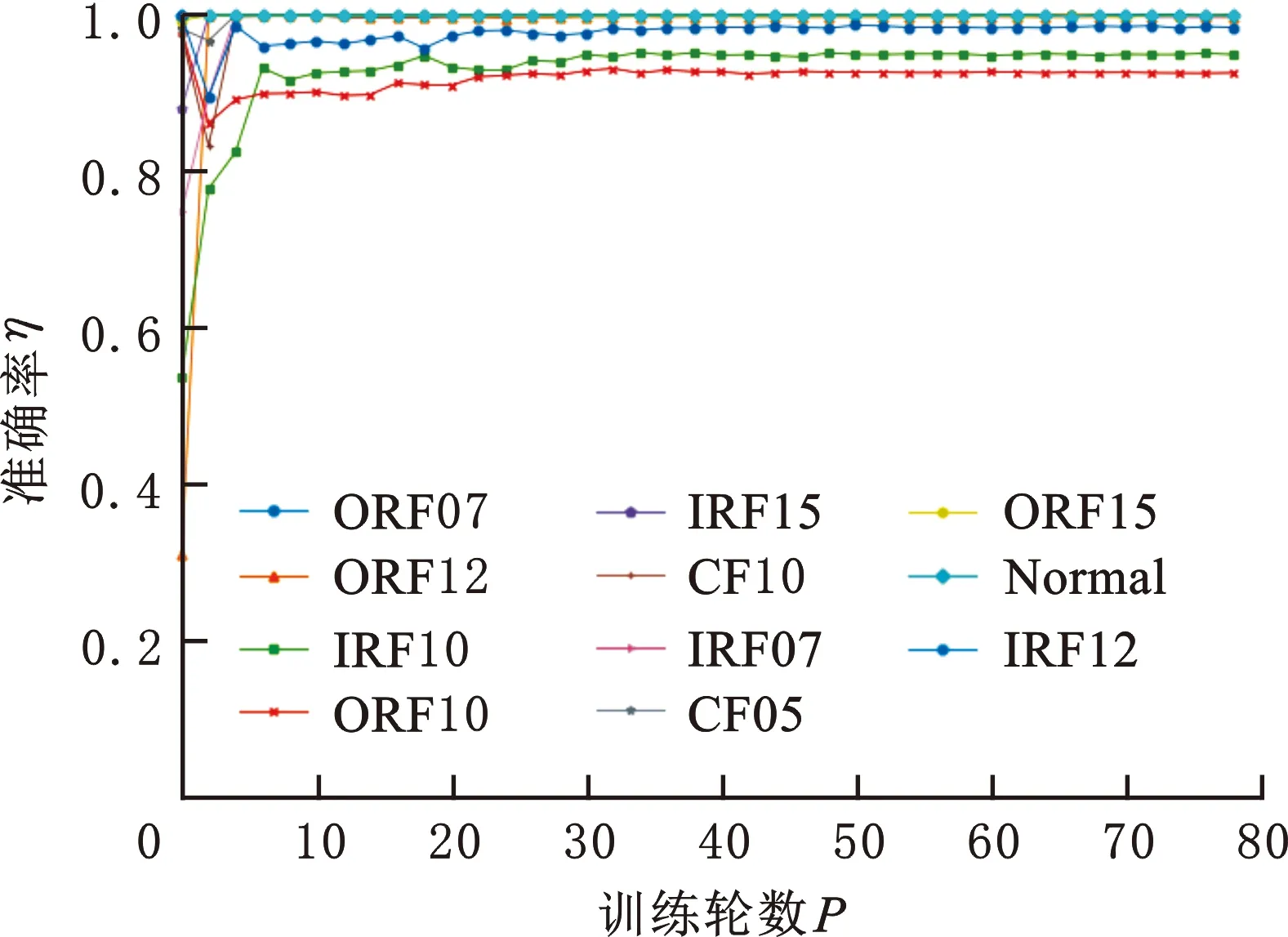
(b)数据集OA2+生成集GA2

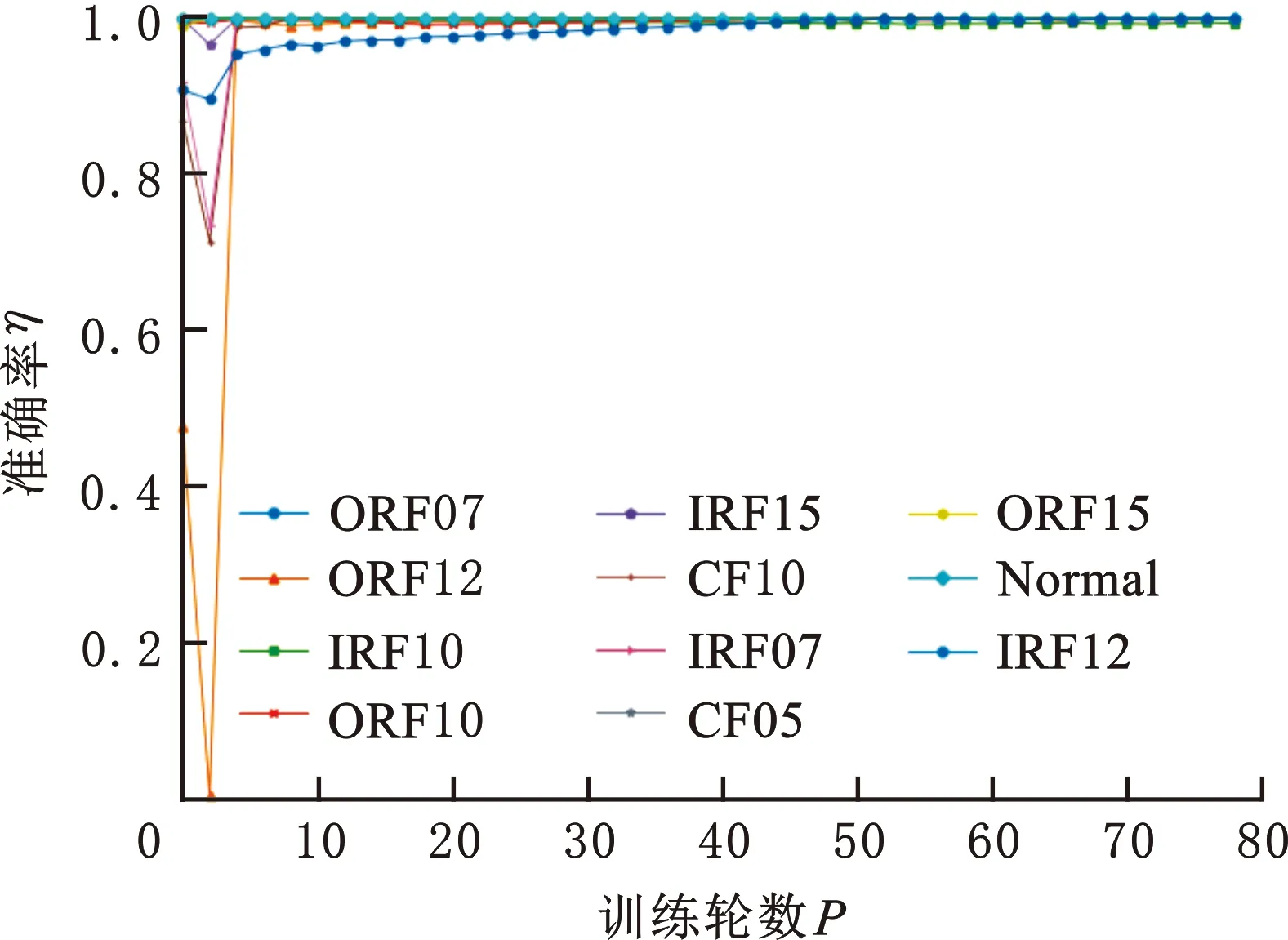
(c)数据集OA2+生成集GB2图7 不同故障的训练准确率曲线Fig.7 Accuracy curve of each fault during training process

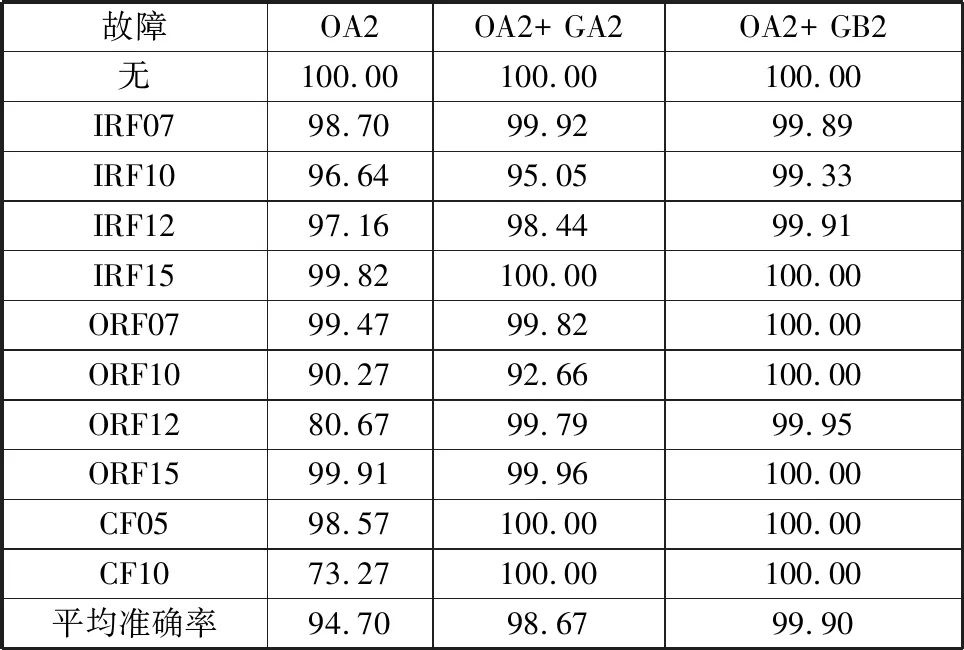
表7 不同故障的准确率

3 对比分析

为了检验本文方法的有效性，将本文方法与1D-CNN[14]、e2e-LSTM[15]、CFVS-SVM(commonplace features of vibration signals)，以及FFT-CNN等4种故障诊断方法进行对比试验。测试在同一台计算机进行，其配置为Windows10操作系统、Intel i5-9400F CPU、16G RAM。对比试验采用的数据集1为2.1节的CWRU数据集、数据集2为2.2节所述数据集，2个数据集的训练集和测试集的划分与上一节保持一致，实验结果如表8所示。

由表8可以看出，不均衡样本条件下，1D-CNN和e2e-LSTM的故障诊断准确率较低。这两种方法均采用神经网络对信号原始数据直接提取特征，在数据量足够的情况下可以有效提取故障特征，但在数据失衡的条件下无法有效提取故障特征、过拟合严重，1D-CNN和e2e-LSTM在数据集1的状态辨识准确率分别为66.03%和65.77%；在多通道数据集2上，这2种方法模型准确率更低，准确率分别为44.13%和22.62%，由此可见，这两种模型出现严重过拟合且泛化能力差。CFVS-SVM和FFT-CNN在输入神经网络前进行了时频域的特征提取，大幅度降低了神经网络提取特征的难度，在少样本情况下对提高模型准确率有所帮助，但仍无法解决过拟合问题。CFVS-SVM和FFT-CNN针对数据集1的模型辨识准确率分别为92.54%、93.08%，对数据集2的模型辨识准确率分别为98.82%、97.98%，仍无法达到很好的效果。SA-ACGAN对2个数据集的准确率分别为99.66%和99.90%，呈现出优异的泛化性能。SA-ACGAN模型生成的优质数据既弥补了数据不足导致的模型泛化性和鲁棒性差的问题，又解决了故障诊断实时性问题。所有额外步骤均在模型训练阶段，故障处理过程无需额外步骤。本文方法的故障诊断模型仅为简单的BP模型，单次诊断时间0.09s远远小于其他方法。上述试验表明BP算法在拥有足够高质量的样本数据后亦能达到复杂算法的故障识别效果。

4 结论

(1)通过衡量本文SA-ACGAN模型的生成器与判别器之间的相对性能，优化了模型训练过程中的生成器性能，动态调节两者之间的平衡，使训练收敛过程更稳定、迅速。

(2)在样本不均衡的条件下，用本文方法生成数据、训练故障诊断模型的故障检测性能明显优于用原始数据和ACGAN方法生成数据训练的故障诊断模型，且模型训练过程中，使用本方法生成数据训练的模型准确率随迭代次数的增加变化平稳，显示出良好的收敛特性。

(3)本文方法仅在训练时通过生成样本来提高BP模型性能，诊断时并未增加额外的计算量。