大型部件的多机器人合作搬运协同导引控制

武 星 余文康 楼佩煌 楼航飞 翟晶晶 胡子寒

南京航空航天大学机电学院，南京，210016

0 引言

异形重载大部件的搬运移载操作普遍存在于大型装备的生产和运输环节。例如，大型飞机的生产过程中，既存在大质量、大尺寸的机身类部件，也存在大尺寸、小刚度的机翼类部件。用于支承定位机翼类部件的工装夹具可能比部件本身的载荷大得多。飞机部件的工装夹具规格多，难以达到类似汽车生产的标准化程度。大型飞机部件的小批量生产模式下，针对数百种工装分别设计开发不同的重载搬运机器人是极不现实的。因此，采用多机器人系统合作搬运异形重载大部件具有十分重要的现实意义。

多机器人合作搬运是指采用多个机器人共同支承一个目标对象，通过机器人之间的协同运动控制来保证组群移动的一致性，实现目标对象的移动。机器人与目标对象的连接方式有抓取[1-3]、拖拉[4-5]、搬抬[6-7]以及推动[8]等。

合作搬运可视为动态环境下具有约束条件的多机器人系统编队控制问题，参与搬运的每个机器人之间的相对位置不变，并具有相同或协调的运动速度和方向[9-10]。如果每个机器人能沿各自期望轨迹达到目的地，且机器人编队能保持编队队形不变，则目标对象作为一个整体能被搬运到目的地。合作搬运可采用领航者-跟随者(leader-follower)策略[6，11-13]、基于行为(behavior-based)法[14]和虚拟力/结构(virtual force/structure)法[15-17]等多机器人编队控制方法。相对于其他编队控制方法，领航者-跟随者策略在多机器人系统中获得了广泛应用。

相对于常规的编队控制方法，合作搬运对机器人位姿误差非常敏感。针对2台轮式机器人的合作搬运，YAMAGUCHI等[4]采用转动副连接2台轮式机器人阿克曼底盘与1个搬运对象，并基于运动学模型的链式变换提出一种新型反馈控制律。针对2台人形机器人的合作搬运，LOUIS等[7]提出了一种包含全局规划器、局部规划器、零力矩点预测控制器和手臂柔顺控制器的协同控制架构。针对多无人机的合作搬运，UMEMOTO等[3]采用无人机自带的转子护罩夹持搬运对象，通过接触力分配及分布式扰动观测控制调整搬运对象的位姿；LIU等[5]对搬运对象采用无人机绳系连接方式，研究了基于张力分布算法的轨迹规划，以及基于扩展状态观测器的反馈控制。

上述合作搬运都涉及搬运方式与控制方法，但文献却均未关注合作搬运过程中导引与控制的协同问题。因此，笔者以轮式机器人的合作搬运为对象，对协同导引控制构型、模型、架构与方法等方面开展了一系列研究。

1 导引控制构型

导引控制构型研究主要分析不同传感器布局和驱动轮(常规轮或以Mecanum轮为代表的全向轮)配置的组合对协同导引控制性能的影响。多机器人系统的组成单元既可以是单台移动机器人，也可以是具有导引、控制和驱动功能的导引驱动单元，如图1所示。该单元包含上层的弹性减振装置和下层的导引驱动底盘，底盘两侧对称安装2个由伺服电机(6)和链轮机构(8、9)驱动的差速驱动轮(7)，并在前方安装有一个视觉导引相机(10)。

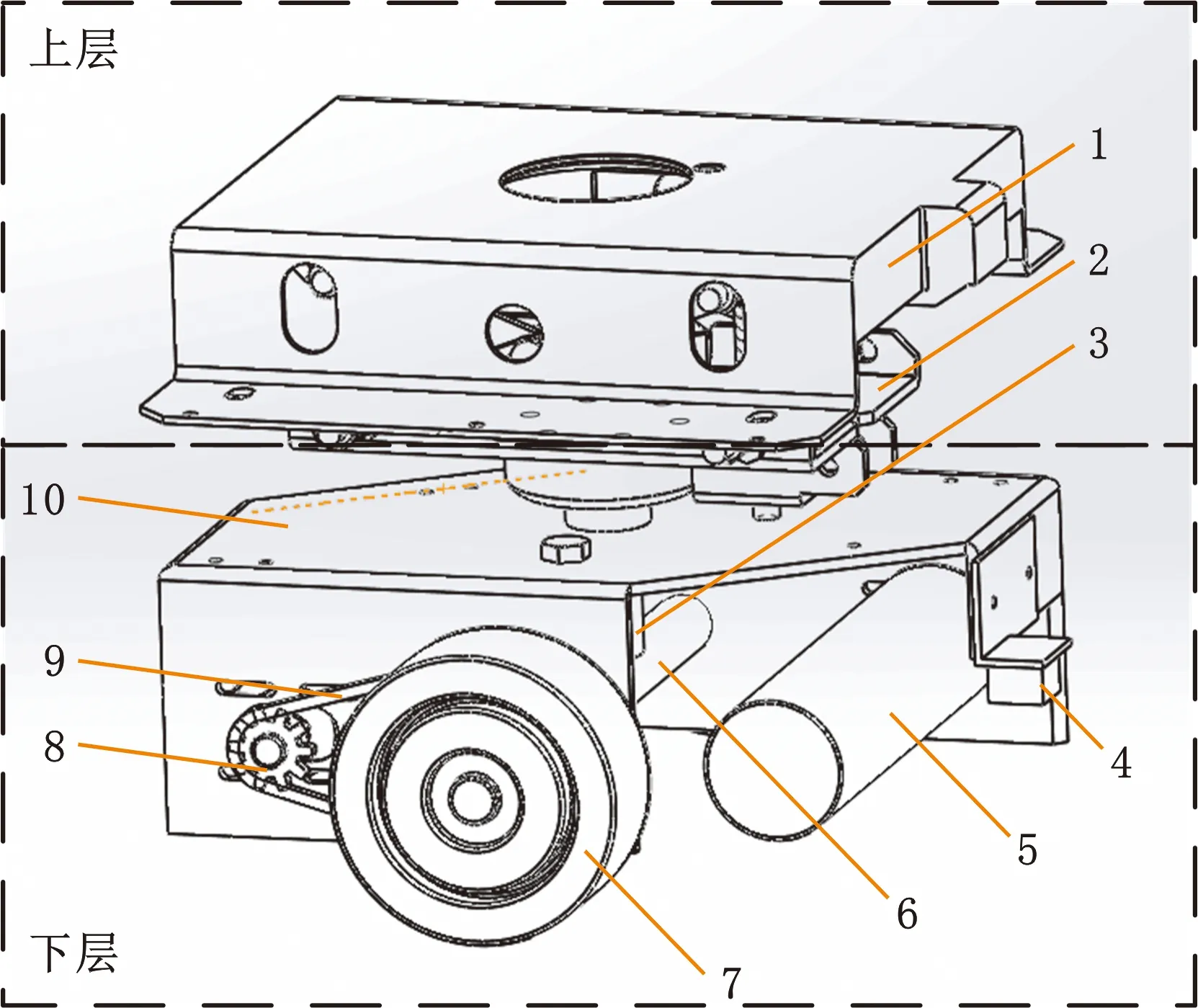
1.顶板 2.底板 3.垂直轴 4.导引相机 5.电机 6.水平轴 7.驱动轮 8.小链轮 9.链条 10.转向架图1 导引驱动单元Fig.1 Guided driving unit

根据传感器布局和驱动轮配置的不同，本文提出3种导引控制构型：单目-双驱动、双目-双驱动、双目-多运动副全向。采用多个导引驱动单元组成合作搬运构型时，最直观的方案为2个驱动单元前后布置并在2个驱动单元间安装视觉导引相机，如图2所示。由于驱动单元均无导引相机，因此前部的驱动单元(驱动单元1)只能依靠导引相机获取整个机器人与导引路径的位姿偏差，导致偏差数据不可避免地存在滞后。即使采用融合偏差智能转化和指数稳定控制的混合控制律[18]，合作搬运构型的路径跟踪性能仍受位姿偏差检测滞后的影响，可见导引控制构型对运动控制方法具有很大影响。

图2 单目-双驱动构型Fig.2 Mono-camera dual-unit configuration

单目-双驱动构型的根本问题在于导引相机与驱动单元的分离。更有利于导引控制的方案是将导引相机配置于驱动单元前方，如图1所示，该导引驱动单元本质上是一种具有感知、规划、控制和驱动的机器人。将多个导引驱动单元按直线布置，构成合作搬运构型，如图3所示。为进行协同运动控制，需要针对多个单元上的导引相机进行传感器标定，即利用多目视觉系统标定方法[19]建立各个视觉测量坐标系与多机器人系统测量坐标系、控制坐标系之间的变换关系。这是采用双目-双驱动构型进行合作搬运的前提条件。

图3 双目-双驱动构型Fig.3 Dual-camera dual-unit configuration

由于采用两轮差速驱动方式，因此导引驱动单元受到非完整运动约束，这给路径跟踪控制带来困难。双目-双驱动构型中，2个单元分别采用转动副与系统平台相连。该构型的转动自由度仅允许多个单元之间具有不同的姿态角，即在协同运动中仅可存在微小的姿态角误差。为进一步消除位置误差对机器人合作搬运的不利影响，即协同运动中可能存在的微小距离误差，笔者开发了导引相机中心配置的Mecanum轮全向移动机器人，并通过转动副和移动副连接多个全向机器人，组成双目-多运动副全向构型，如图4所示。该构型包括机器人上的转动副、连接运载工装与第二转动副的第一移动副，具有容许全向机器人姿态角误差和位置误差的两个自由度，有利于协同运动控制。

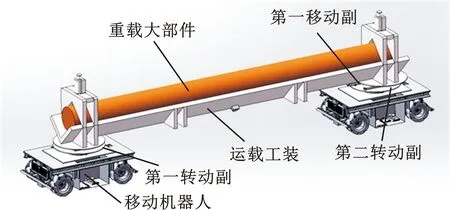
图4 双目-多运动副全向构型Fig.4 Dual-camera multi-kinematic-pair omni-directional configuration

2 运动控制模型

为进行合作搬运的协同运动控制，针对双目-双驱动构型和双目-多运动副全向构型分别建立运动控制模型。

2.1 双目-双驱动运动模型

如图5所示，点Gi、XiGiYi分别为导引驱动单元i(i=1，2)的中心和局部坐标系，X0G0Y0为系统坐标系，线段G1G2的长度为b，G0为其中点。

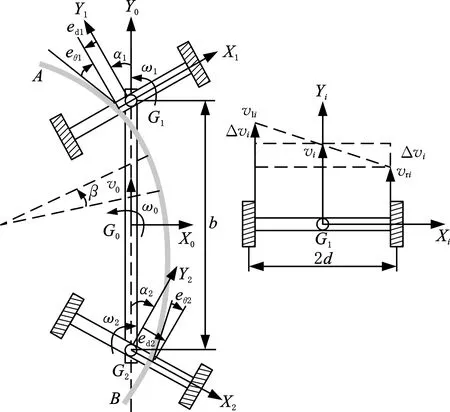
图5 双目-双驱动运动简图Fig.5 Dual-camera dual-unit kinematic sketch

对于导引驱动单元i，edi、eθi分别是它与导引路径的侧向位置偏差和姿态角偏差，αi是它与系统平台的转角差，vli、vri是其左右驱动轮的线速度，vi是其中心的线速度，Δvi是vli和vri的速度差，ωi是由差速产生的转向角速度。v0、ω0分别是系统平台的线速度和转向角速度。d为两驱动轮间距的一半。

导引驱动单元采用两轮差速驱动方式，因此线速度与转向角速度之间存在以下关系：

vi=(vli+vri)/2

(1)

ωi=(vli-vri)/(2d)=Δvi/d

(2)

针对直线型或小曲率导引路径，路径偏差与单元速度之间存在以下关系：

(3)

(4)

针对图5所示的多刚体机械系统，要保证Y0方向上2个导引驱动单元的距离不变，则2个导引驱动单元的速度需满足刚体连接约束：

v1cosα1=v2cosα2

(5)

系统平台的转向角速度为

(6)

单元i相对于系统平台的转角差变化率为

(7)

综上，可得双目-双驱动运动模型：

(8)

2.2 双目-多运动副全向运动模型

该构型采用的全向移动机器人i在全局坐标系中具有3个独立的运动速度即vxi、vyi和ωi，如图6所示。每个机器人中心安装1个垂直向下的导引相机，两机器人与运载工装通过转动副连接于点Oi，机器人与运载工装的转角差为αi。跟随机器人与运载工装间设置有移动副，所以两机器人间的Y向距离可能在运动过程中发生变化，假设其期望值为L0，实际值为L，则纵向距离偏差ΔL=L-L0。以杆件O1O2上的运载工装为对象，建立杆件坐标系O2XY，其转向角速度为ω0。

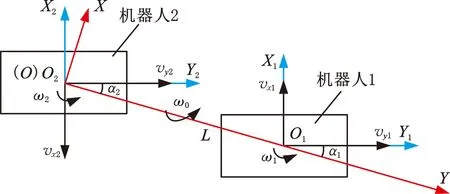
图6 双目-多运动副运动简图Fig.6 Dual-camera multi-kinematic-pair omni-directional kinematic sketch

与图5类似，edi、eθi分别为全向移动机器人与导引路径的侧向位置偏差和姿态角偏差。假设控制周期为T，则单个移动机器人的运动模型为[20]

(9)

(10)

机器人与运载工装通过转动副连接，机器人与运载工装的转角差αi变化率取决于机器人与运载工装的转角差变化率(式(7))。运载工装的转向角速度为

(11)

跟随机器人与运载工装间还设置有Y向移动副，将机器人的平动速度沿杆件坐标系O2XY投影，如图6所示，则两机器人间的Y向距离误差变化率为

(12)

与双驱动构型的刚体连接约束(式(5))相比，多运动副全向构型存在移动副，因而增加了1个纵向的移动自由度。综上，可得双目-多运动副全向运动模型：

(13)

3 协同控制方法

为实现多机器人合作搬运，针对不同运动模型，基于领航者-跟随者策略设计了协同路径跟踪控制架构，研究了2种协同跟踪控制方法。

3.1 双目-双驱动构型

针对式(8)所示的双目-双驱动运动模型，在传感器量程约束、电机驱动性能约束、平台转向半径约束等多约束条件下[13]，直接求解运动模型的控制量是比较困难的。因此，本文融合领航者-跟随者策略、刚体连接约束(式(5))、路径跟踪方法和参数调节方法，设计了协同路径跟踪同构控制架构，如图7所示。运动控制模型构建为一个六输入-六输出的确定性系统：

(14)

式中，Lexi为导引驱动单元i的期望跟踪距离。

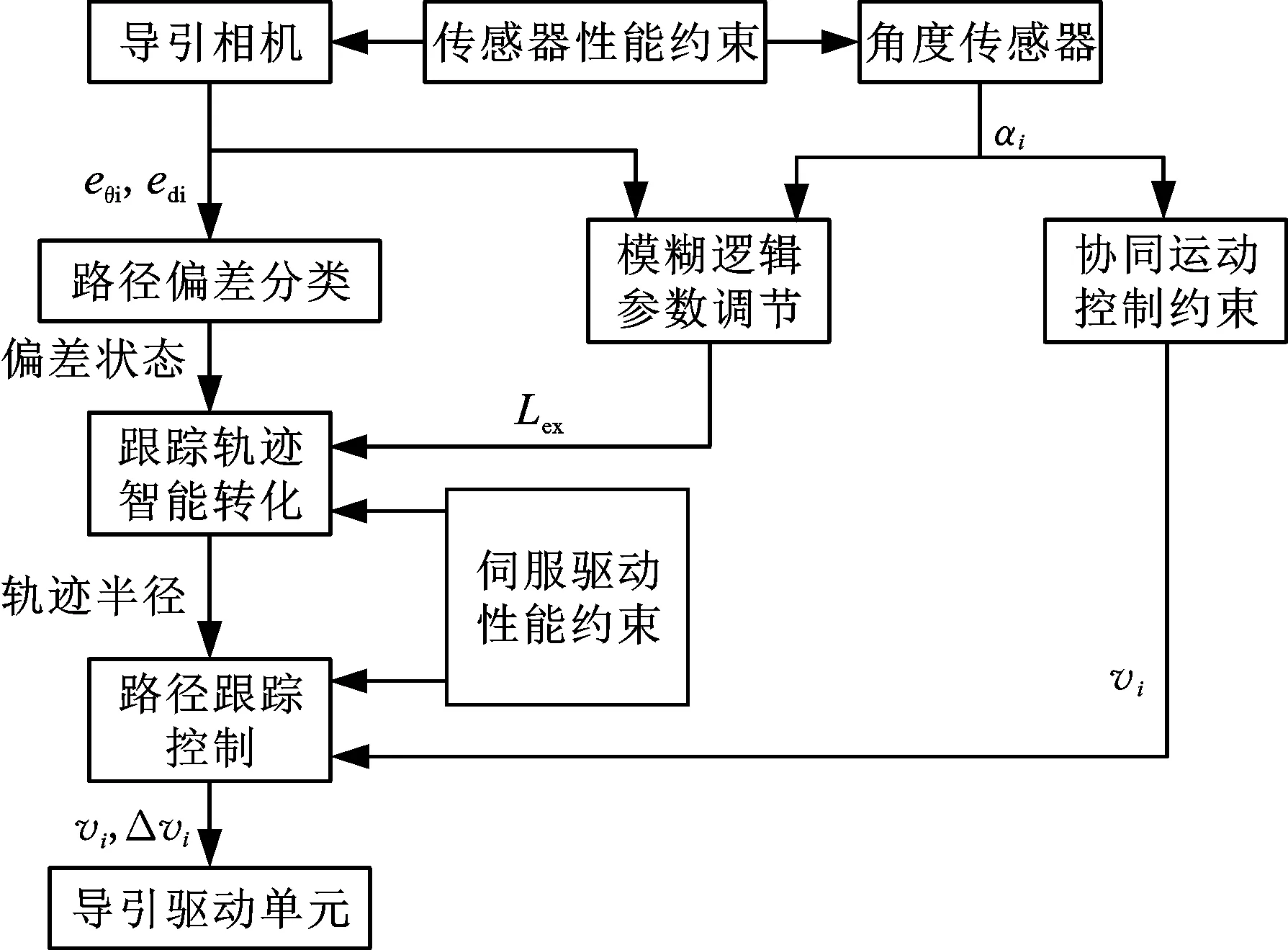
图7 协同路径跟踪同构控制架构Fig.7 Homogeneous control framework for coordinated path tracking

导引驱动单元经过长度为Lexi的期望跟踪距离后，侧向位置偏差和姿态角偏差逐渐消除，导引驱动单元逼近并跟踪导引路径。

如图5所示，将前单元作为领航者，后单元作为跟随者。单元i有独立跟踪导引路径的视觉导引控制系统，产生进行纠偏控制的速度差Δvi。将前单元的线速度v1作为系统平台的运行速度v0。由于刚体连接约束(式(5))的存在，因此后单元的线速度v2取决于前单元的线速度v1，以及两单元的转角差α1和α2。路径跟踪技术用于构建联系速度差Δvi与侧向位置偏差edi、姿态角偏差eθi、期望跟踪距离Lexi的模型。Lexi是反映两单元运动协同度的耦合参数，与本单元的侧向位置偏差、姿态角偏差，以及两单元的转角差有关。

在图7所示的该协同路径跟踪控制架构中，每个单元独立并发地进行视觉导引和路径跟踪的处理，但相互之间的运动行为通过期望跟踪距离Lexi和协同运动控制约束进行耦合联系。Lexi、v2与协同运动控制相关，因此该控制构架可分为两部分：①各单元并行的路径跟踪控制；②多单元之间的耦合参数调节。前者意味着每个单元都可采用相同的导引控制流程(同构控制构架)，它包括路径偏差分类、轨迹转化预测和路径跟踪控制。后者反映了跟随者与领航者的协同运动，是通过运动参数耦合来实现的。

同构控制架构中，每个单元采用相同的导引控制方法。根据路径偏差特征和传感控制约束，定义了6种路径偏差状态及其相关的纠偏轨迹，分析了各种纠偏轨迹相互转化的状态迁移机制，研究了可同步消除侧向位置偏差和姿态角偏差的同步纠偏轨迹，提出了其他纠偏轨迹迁移到同步纠偏轨迹的轨迹控制方法[13，21]，其中，期望跟踪距离是影响路径跟踪控制效率、轨迹转化安全裕度和多机器人运动协同度的耦合参数。为自适应调节该耦合参数，设计了一种二阶模糊逻辑调节器，以单元i的侧向位置偏差edi、姿态角偏差eθi、两单元与系统平台的转角差之差α1-α2为输入，先通过三角隶属度函数进行模糊逻辑推理，再利用重心法输出期望跟踪距离的精确估计值[13]。

3.2 双目-多运动副全向构型

如图6所示，在双目-多运动副全向构型中采用领航者-跟随者策略，前机器人作为领航者，后机器人作为跟随者。每个机器人都有独立跟踪导引路径的视觉导引控制系统，并分别产生进行纠偏控制的侧移速度vxi和转向角速度ωi。领航者的前移速度vy1为合作搬运的领航速度。由于运载工装的移动副允许两机器人沿Y向发生相对运动，因而如式(12)所示，跟随者的前移速度vy2相对于领航者的前移速度vy1具有更灵活的变化过程，而非式(5)所示的严格协调关系。针对双目-多运动副全向构型，设计了一种协同路径跟踪异构控制架构，如图8所示，其中，领航者采用模型预测控制方法，跟随者采用反演控制方法，且反演控制参数由强化学习和神经网络技术调节。

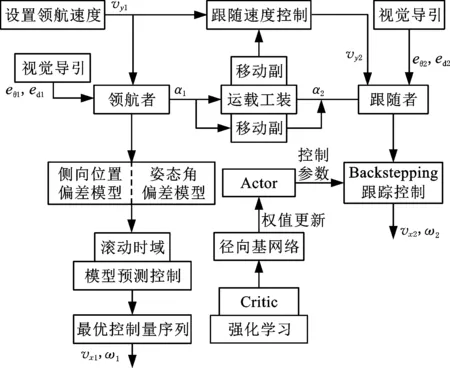
图8 协同路径跟踪异构控制架构Fig.8 Heterogeneous control framework for coordinated path tracking

异构控制架构中，领航者和跟随者采用不同的导引控制方法。领航者根据式(9)、式(10)所示的侧向位置偏差模型和姿态角偏差模型，分别规划N步控制序列，建立预测控制的代价函数，通过二次规划方法求解满足代价函数的最优控制量序列，该序列的第一项控制量作为当前控制周期内路径跟踪的控制量输出[16，22]。

侧向位置偏差模型中，系数hi与姿态角偏差eθi、转向角速度ωi有关。由于全向移动机器人的侧移速度vxi和转向角速度ωi无控制耦合，所以可分别求解ωi、vxi的最优控制量序列。首先，根据式(10)所示的姿态角偏差模型求解ωi的最优控制量序列εθ，并根据该序列预测eθi的变化序列W。其次，根据序列εθ和W计算侧向位置偏差的系数序列H。再次，根据式(9)所示的侧向位置偏差模型求解vxi的最优控制量序列Vx。

跟随者采用反演控制方法同时跟踪地面的导引路径和领航者牵引的运载工装。为保证跟随者的协同运动控制过程具有全局渐近稳定性，设计了如下的跟踪控制律：

(15)

反演控制器设计过程中，侧向位置偏差模型采用了线性化近似处理。为解决模型失真可能引起的控制器性能退化问题，本文采用行动者-评论者(Actor-Critic，AC)强化学习方法对反演控制器中的控制参数k1、k2、k3进行自适应调整，如图9所示。

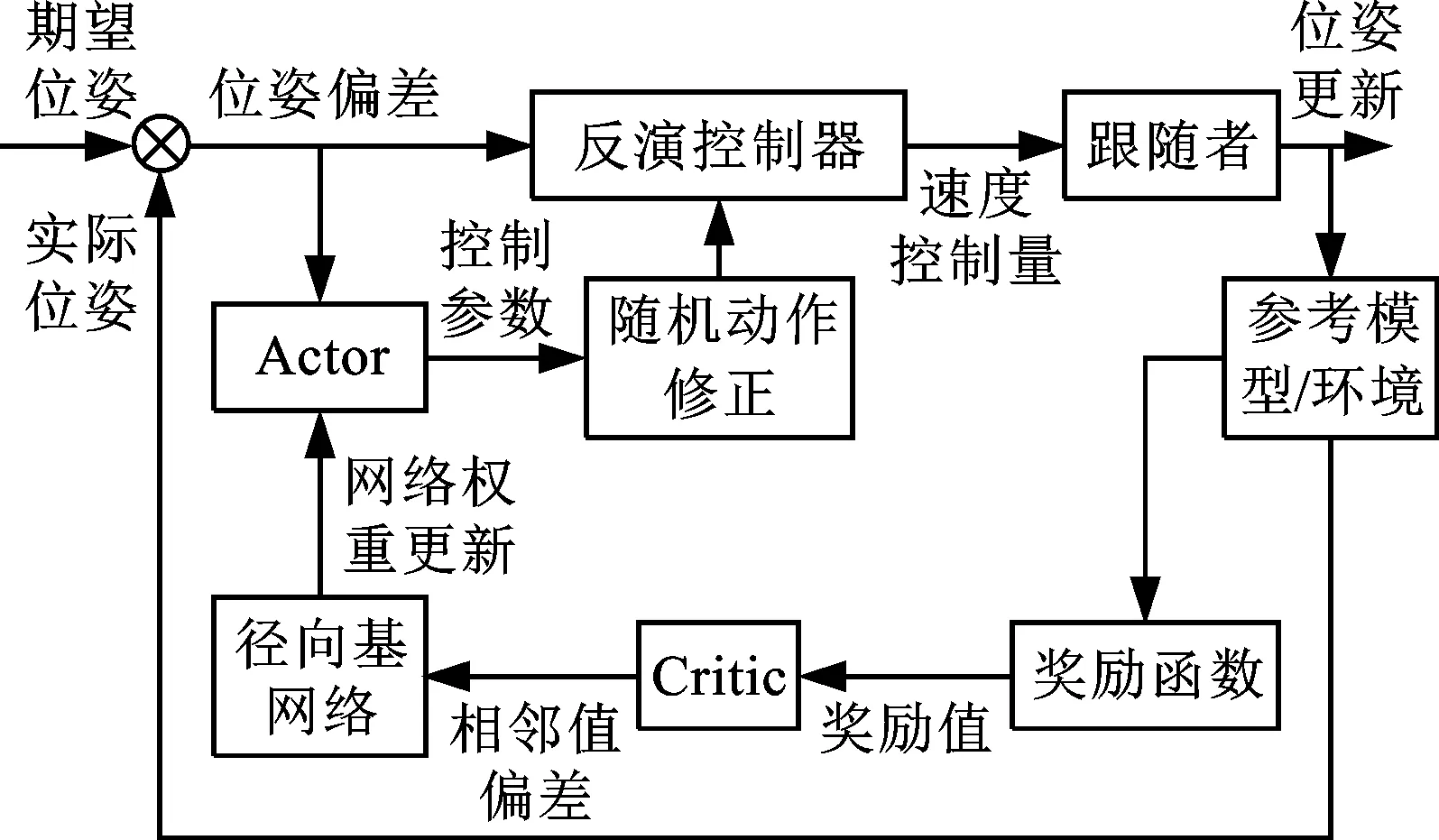
图9 基于强化学习的控制参数自调整Fig.9 Adaptive adjustment of control parameters based on reinforcement learning

强化学习模型中，Actor在连续动作空间内基于概率选择合适的动作，Critic针对参考模型/环境的状态更新来评价actor的行为(给予奖励值)，Actor根据Critic的奖励值来更新行为选择的概率。如图9所示，该模型采用径向基神经网络实现Actor的行为选择即控制参数调整，并实现Critic的环境状态更新(估计下一时刻的机器人位姿偏差)与奖励值计算。采用时序差分算法的相邻状态值函数偏差定义强化学习目标，并通过梯度下降近似估计算法更新神经网络的权重。

4 实验分析

为验证本文所提的协同导引控制构型、模型和方法，设计双目-双驱动构型和双目-多运动副全向构型的多机器人合作搬运原型系统完成协同导引控制实验。

4.1 双目-双驱动构型

双目-双驱动运动构型的原型系统前后布置2个视觉导引驱动单元，如图10所示。系统尺寸为1800 mm×800 mm×360 mm，每个驱动单元采用2台400 W的伺服电机独立驱动φ125 mm的实心轮，原型系统的框架采用4个万向轮作为辅助支撑，有效承载能力为1000 kg。

图10 双目-双驱动原型系统Fig.10 Dual-camera dual-unit prototype

单元i的导引相机实时获取地面导引路径的图像，通过图像DSP(digital signal processor)完成图像分割、目标识别、路径拟合和偏差测量，以25 Hz的频率检测导引驱动单元的侧向位置偏差edi和姿态角偏差eθi，测量精度为±0.5 mm和±0.5°。单元i弹性减振装置的下承载板(图1中的部件2)上安装有角度传感器，以25 Hz的频率测量单元与系统平台的转角差αi，测量精度为±0.1°。嵌入式控制器通过串口接收DSP输出的侧向位置偏差和姿态角偏差，通过AD转换接口读取角度传感器的转角差电压信号；再执行协同路径跟踪控制算法，获得导引驱动单元的线速度和速度差；然后根据差速驱动逆运动学模型求解驱动轮转速，并输出给电机驱动器完成伺服驱动控制。

将地面上设置的一圈蓝色色带作为闭环导引路径，该路径包括4个直线段和1个半径1.2 m的圆弧转弯段。前导引驱动单元的线速度v1为800 mm/s，后单元的线速度v2根据刚体连接约束实时调节。两个单元的初始偏差状态如表1所示。

表1 导引驱动单元的初始偏差状态

协同路径跟踪实验中，两单元在转弯前的直线段、圆弧转弯段，以及转弯后直线段的侧向位置偏差和姿态角偏差变化如图11所示，转角差变化如图12所示。

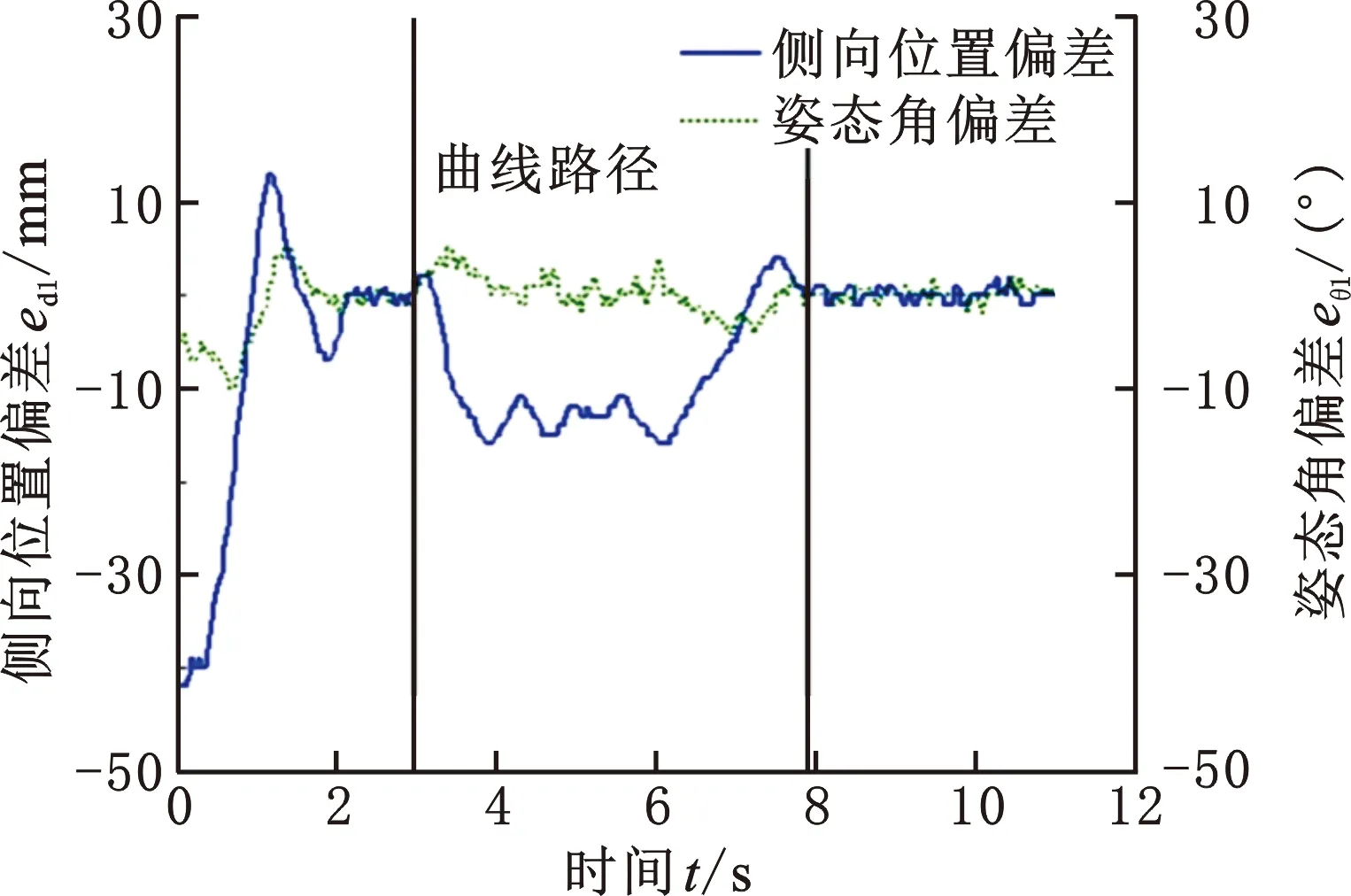
(a)前单元

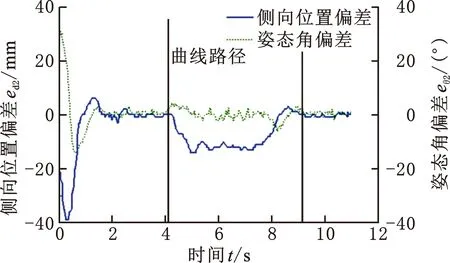
(b)后单元图11 协同路径跟踪的路径偏差Fig.11 Path deviations in coordinated path tracking

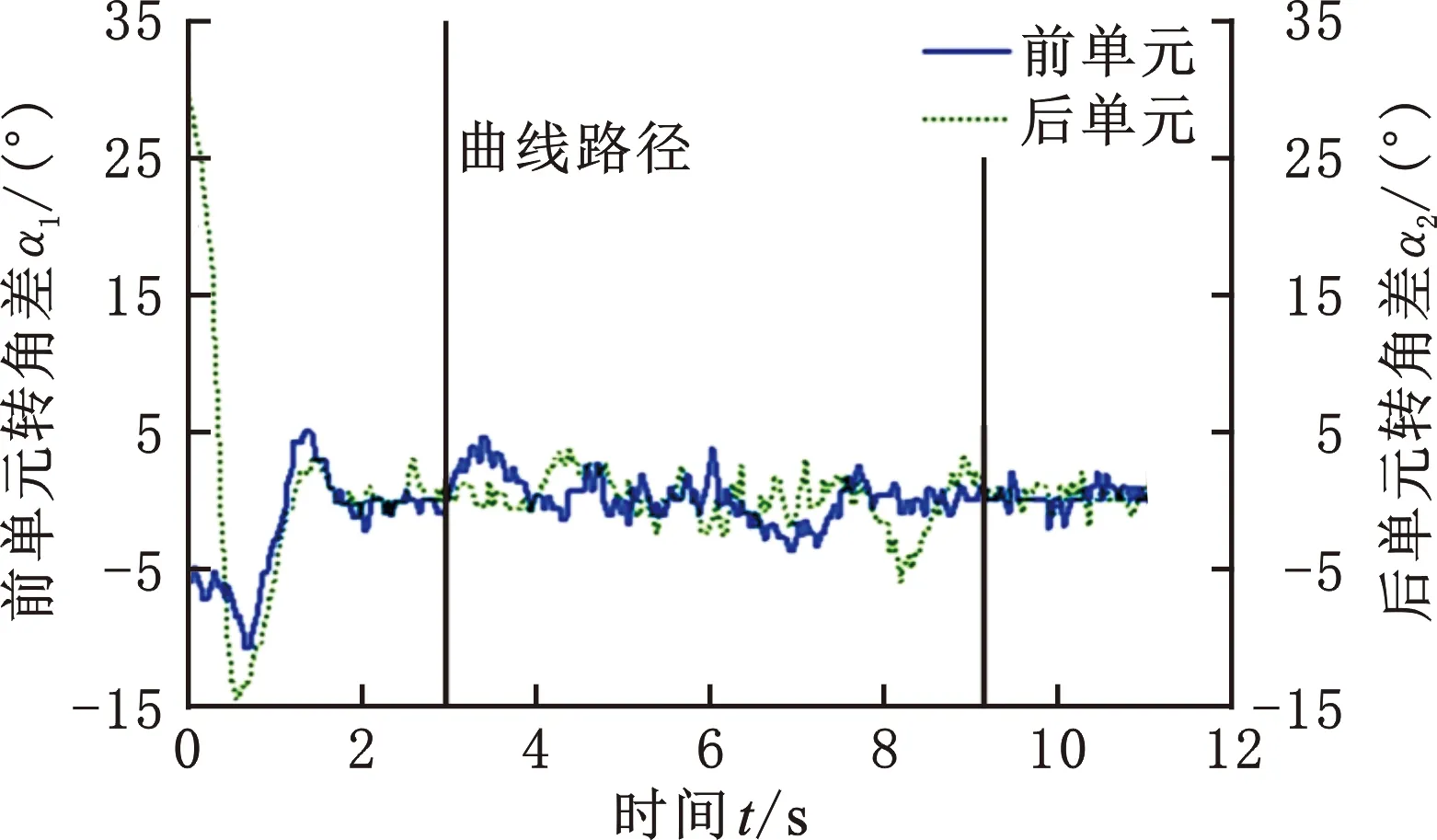
图12 协同路径跟踪的转角差Fig.12 Steering angles in coordinated path tracking

如图11a所示，前单元0～3 s运行在转弯前的直线段上，其纠偏轨迹在6种路径偏差状态之间相互转化，ed1和eθ1由初始值快速减小；2.28 s时，前单元沿同步纠偏轨迹运行，将两种路径偏差消除到|ed1|<2 mm，|eθ1|<2°的稳定状态。前单元在3 s后进入圆弧转弯段，ed1急剧反向增大到负极值，其纠偏轨迹在2种路径偏差状态之间反复转化，整个圆弧路径的跟踪精度为11 mm<|ed1|<16 mm，|eθ1|<4°，这比直线路径的跟踪精度稍低。7.96 s时，前单元进入转弯后的直线段，其纠偏轨迹在5种路径偏差状态之间相互转化，最后进入直线路径的稳定跟踪状态。

如图11b所示，后单元在转弯前的直线段经历了4种纠偏轨迹的转化而进入稳定跟踪状态，直线路径的跟踪精度与前单元相似。4.12～9.16 s范围内，后单元在圆弧转弯段上运行，也通过2种纠偏轨迹在2种路径偏差状态之间反复转化，圆弧路径的跟踪精度也与前单元相似。由图11可知，各种纠偏轨迹相互转化的状态迁移机制是有效的，同步纠偏轨迹可同时有效消除侧向位置偏差和姿态角偏差。

如图12所示，在转弯前的直线段上，转角差α1、α2的初始值分别为-5°和30°。由于后单元应跟随前单元的运动，所以α2快速减小到0并反向增大以趋近α1。随后，α2跟随α1依次经历峰值和谷值而向0收敛，|α1|<3°时，α2在-3°～3°范围内波动。圆弧转弯段内，为保证两导引驱动单元的速度瞬心重合，导引驱动单元与系统平台间的转角差需满足多体机械系统的运动约束。系统平台的转弯半径越小，单元与系统平台间的转角差越大，因此，两单元在圆弧路径上的转角差明显大于其在直线路径上的稳态值。两单元重新进入直线路径后，转角差快速减小至其稳态值。

4.2 双目-多运动副全向构型

双目-多运动副全向构型的原型系统前后布置2个Mecanum轮全向移动机器人，如图13所示。前后机器人分别通过第一转台和第二转台连接管状大部件，且在第二转台的上下两块圆形承载板之间设置有导轨。全向机器人的尺寸为1090 mm×720 mm×360 mm，分别采用4台750 W的伺服电机独立驱动φ254 mm的Mecanum轮。管状大部件的尺寸为φ160 mm×3000 mm，转台直径为600 mm，导轨长度为430 mm。

全向机器人i中心垂直向下安装有导引相机，实时获取地面导引路径的图像，再通过图像DSP识别侧向位置偏差edi和姿态角偏差eθi。机器人i的转台安装有角度传感器，测量机器人i与管状大部件的转角差αi。第二转台导轨副安装的距离传感器以25 Hz的频率测量2个机器人之间的纵向距离偏差ΔL，测量精度为±0.01 mm。嵌入式控制器采集DSP和其他传感器输出的侧向位置偏差、姿态角偏差、转角差、Y向距离误差等数据；再通过协同路径跟踪控制算法，计算全向机器人的平移速度和转向角速度；最后根据Mecanum轮驱动逆运动学模型求解Mecanum轮转速，并输出给电机驱动器完成伺服驱动控制。

以地面设置的蓝色色带作为闭环导引路径(包括4个直线段和1个半径1.5 m的圆弧转弯段)。前机器人的前移速度vy1为400 mm/s，后机器人的前移速度vy2根据纵向距离约束实时调节。协同路径跟踪算法分别通过预测控制和反演控制计算侧移速度vxi和转向角速度ωi。两机器人的初始偏差状态如表2所示。

表2 全向机器人的初始偏差状态

该合作搬运原型系统在闭环导引路径上完成了连续多圈的协同路径跟踪实验。以第一圈第一个圆弧转弯段为例，分析转弯前的直线段、圆弧转弯段、转弯后的直线段中，两机器人的侧向位置偏差、姿态角偏差，以及机器人间纵向距离偏差的变化，其中，前机器人的侧向位置偏差和姿态角偏差变化如图14所示。

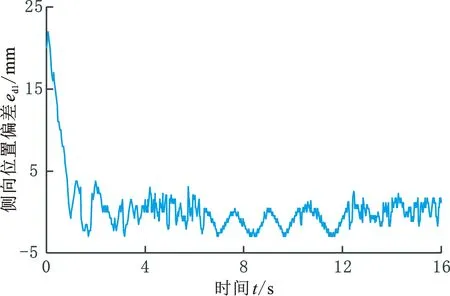
(a)侧向位置偏差

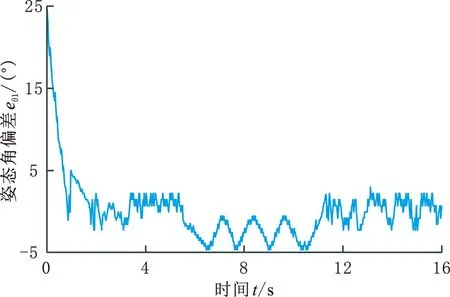
(b)姿态角偏差图14 前机器人路径偏差Fig.14 Path deviations of leader robot

0～6 s内，前机器人在转弯前的直线段上运行，预测控制器自2.5 s后进入稳态，|ed1|<3 mm，|eθ1|<3°。6～12 s时，前机器人进入圆弧转弯段。由于Mecanum轮机器人的全向移动能力，ed1并未出现类似差速机器人的急剧反向增大，而是在-5～0 mm 之间周期性波动。同时，eθ1在-5°～0°之间周期性波动，全向机器人具有较高的跟踪控制精度。12 s后，前机器人进入转弯后的直线段，ed1、eθ1快速减小至其稳态值。

针对多圈协同路径跟踪的实验数据进行统计处理。在直线段上，前机器人的侧向位置偏差均值为0.7 mm，均方差为1.2 mm；姿态角偏差均值为0.8°，均方差为1.2°。在圆弧转弯段上，前机器人的侧向位置偏差均值为-1.9 mm，均方差为2.1 mm；姿态角偏差均值为-2.6°，均方差为1.2°。可见，前机器人在直线段上的两种偏差均值和均方差都小于圆弧转弯段。

后机器人在路径跟踪过程中采用反演控制法，其控制参数可设置为固定值或通过AC强化学习方法优化。在实验中对比了这两组控制参数的跟踪控制效果，侧向位置偏差和姿态角偏差的变化如图15所示。

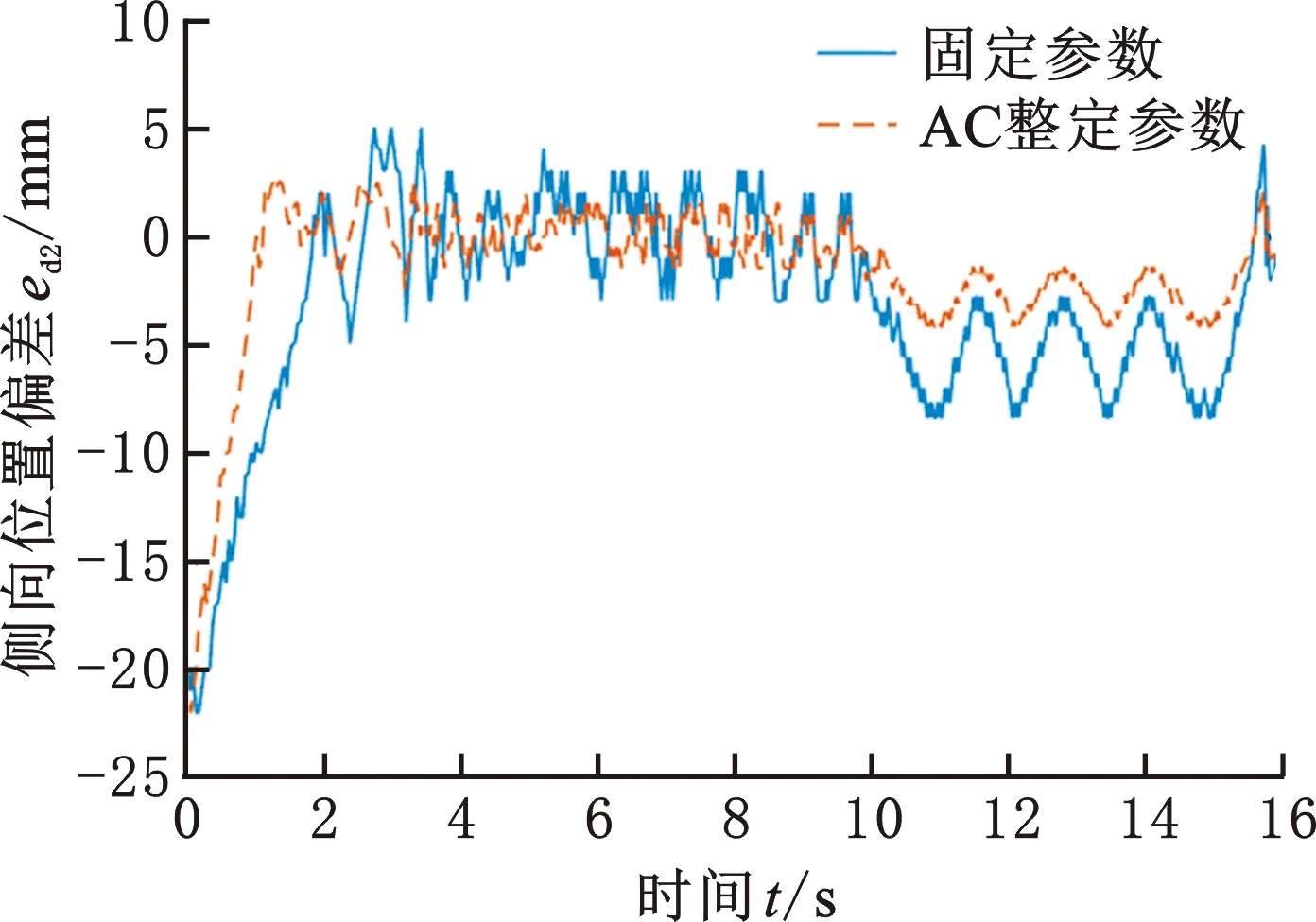
(a)侧向位置偏差

如图15所示，强化学习优化后，ed2、eθ2在直线路径上更快收敛到稳态值，且其稳态偏差明显减小。后机器人在圆弧转弯段上运行时，固定参数控制下的ed2在-9～0 mm 之间周期性波动，而强化学习优化后的ed2仅在-3～0 mm之间波动，圆弧转弯段的跟踪误差明显减小。

分别对固定参数控制与强化学习优化控制的多圈协同路径跟踪实验数据进行统计处理。采用固定参数控制时，后机器人在圆弧转弯段上的侧向位置偏差均值为-5.6 mm，均方差为1.9 mm；姿态角偏差均值为-2.7°，均方差为1.7°。采用强化学习优化控制时，后机器人在圆弧转弯段上的侧向位置偏差均值为-2.8 mm，均方差为1.0 mm；姿态角偏差均值为-1.8°，均方差为1.1°。采用强化学习优化控制后，后机器人两种偏差的均值和均方差都显著减小。

协同路径跟踪实验中，两机器人之间的纵向距离偏差变化如图16所示。强化学习优化后，ΔL在直线路径上更快收敛到稳态值，且其稳态偏差明显减小。无论两机器人位于导引路径的直线段还是圆弧段，或是一个机器人位于直线段而另一个位于圆弧段，ΔL的波动幅值都没有明显的变化，但强化学习优化后的ΔL波动明显减小。对比实验的ed2、eθ2和ΔL验证了强化学习优化控制参数的有效性。

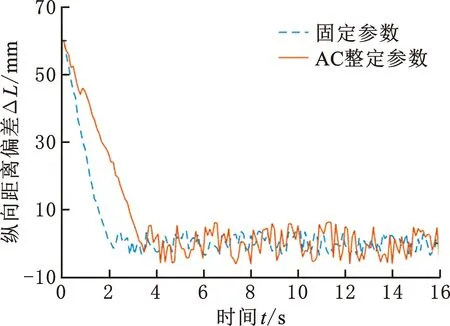
图16 机器人间纵向距离偏差Fig.16 Longitudinal distance deviation between robots

进一步，对协同路径跟踪的实验数据进行统计分析，采用固定参数控制时，ΔL的均值为-0.03 mm，均方差为3.78 mm；采用强化学习优化控制时，ΔL的均值为-0.04 mm，均方差为2.26 mm。可见，采用强化学习优化控制后，ΔL的均值虽然与固定参数控制时接近，但均方差显著减小，说明采用强化学习后，机器人间纵向距离的控制过程比较平稳。

对比双目-双驱动构型与双目-多运动副全向构型的协同路径跟踪实验数据，发现两者在直线段上的稳态侧向位置偏差和姿态角偏差基本相同。双目-多运动副全向构型采用全向Mecanum轮并在两机器人间增加纵向移动自由度，这有效增强了机器人直接消除侧向位置偏差的灵活度，显著提高了合作搬运系统对ΔL的容忍度。因此，双目-多运动副全向构型中的两机器人在圆弧转弯段上的侧向位置偏差显著减小，且跟随者采用强化学习优化控制后的侧向位置偏差更小。协同路径跟踪的实验结果验证了所提协同导引控制构型、模型、架构与方法的可行性和有效性。

5 结论

采用多机器人系统合作搬运异形重载大部件具有显著的作业灵活性和工况适应性。首先，研究了单目-双驱动、双目-双驱动、双目-多运动副全向等合作搬运导引控制构型，分析了不同传感器布局对协同导引控制的影响。其次，针对后两种构型分别建立了多输入-多输出运动控制模型，并基于领航者-跟随者策略，设计了协同路径跟踪的同构控制架构和异构控制构架。同构架构下，两导引驱动单元采用偏差转化预测控制方法，其跟踪距离参数由模糊逻辑调节器优化。异构架构下，领航者采用模型预测控制方法，跟随者采用反演控制方法，反演控制的参数由AC强化学习方法优化。最后，针对双目-双驱动和双目-多运动副全向构型，开发了多机器人合作搬运原型系统，完成了协同导引控制实验，实验结果验证了所提协同导引控制构型、模型、架构与方法的可行性和有效性。

值得注意的是，上述构型、模型与架构都是针对2个导引驱动单元或全向移动机器人进行分析与推导的。虽然理论上可以推广到3个及以上机器人的情况，但无论是双目-双驱动构型还是双目-多运动副全向构型，其系统控制模型都面临协同运动约束不断增加的问题，这将导致协同导引控制的难度逐渐增大。因此，该问题需要在未来工作中继续深入研究。